On Accounting for Evaporation or Infiltration Free Surface in Some Problems of Filtration Theory

Within the theory of the flat established filtering of an incompressible fluid under Darci’s law in homogeneous and isotropic soil some tasks connected with currents in the presence of evaporation or infiltration on a free surface of subsoil waters are considered.

The task about flow of a groove was for the first time studied by N.E. Zhukovsky [1] where Kirchhoff’s method altered by it in the theory of streams was used for a solution of tasks with a free surface and special analytic function which is widely used in the theory of filtering is entered. Since function, and a task and a groove bear a name of Zhukovsky [2–6]. Work [1] opened a possibility of mathematical modeling of the movement of subsoil waters under Zhukovsky’s groove and laid the foundation for researches of the specified class of filtration currents (see, for example, reviews [2- 6]).

It should be noted that in tasks about flow of a groove of Zhukovsky application of function of Zhukovsky only then results in effective results when in addition to a free surface the border of area of a current contains only horizontal lines of equal potential and vertical lines of current (V.V. Vedernikov, F.B. Nelson Furriers, S.N. Numerov, V.I. Aravin, etc.). However in actual practice hydrotechnical construction [2-5], the irrigated agriculture [2,4,7], etc. directly under integumentary deposits along with horizontal pressure head water-bearing layers more high-permeability [7] also horizontal waterproof inclusions often meet that radically affects the nature of filtration currents [8–12].

At the same time so far, there are no works devoted to a special research of impact of evaporation or infiltration on filtration processes. Accounting of these important physical factors for the present did not become broad property of exact analytical solutions.

In the presented work on the example of two limit filtration schemes which arise at flow of a groove of Zhukovsky, the impact of evaporation or infiltration on a current picture is studied.

The first limit scheme corresponds to a case when the layer of earth on all the extent is spread by the impenetrable horizontal basis and from a free surface there is a uniform evaporation of intensity ε (0 <ε <1). The current is provided with water inflow from the left part of a band of flooding with a liquid layer, invariable on time. As the right edge of a band of flooding serves the impenetrable vertical screen in the form of a groove of Zhukovsky which basis is located in layer, at the same time the static height of a capillary raising of a subsoil water can be considered (Figure 1(a)).

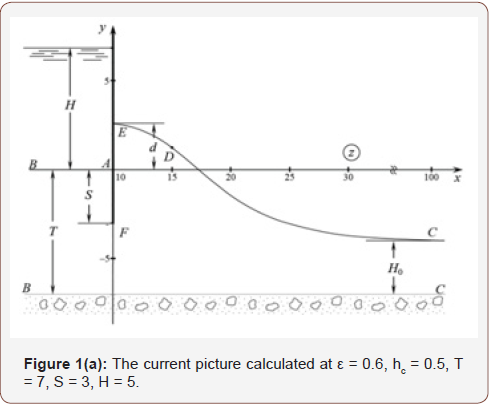
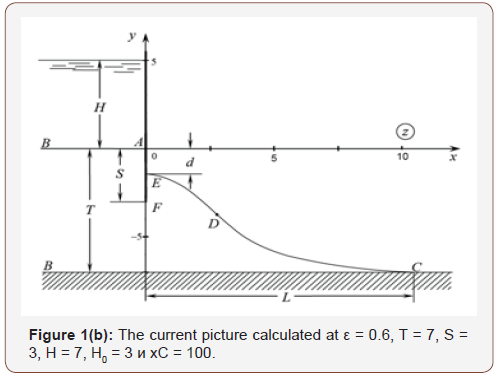
In the second limit scheme the layer of earth is spread by well permeable pressure head aquifer in which pressure has constant H0 value, and on a free surface there is a uniform infiltration of intensity ε [13-16]. Far from a groove (at x →∞) the curve of a depression is horizontal and located at H0 height over an aquifer (Figure 1(b)).

The exact solution of a task on a fluid influx to the imperfect well with the flooded filter (i.e. an axisymmetric task) or the tubular well representing an impenetrable pipe with the filter in some (usually lower) its part is connected with great mathematical difficulties and so far is not found. Therefore, in due time as first approximation to a solution of similar tasks by P.Ya. Polubarinova- Kochina, V.G. Pryazhinska, V.A. Postnov and V.N. Emikh [2,6,7,17,18] considered some corresponding flat task analogs about filtering in a rectangular jumper with partially impenetrable vertical wall and to imperfect gallery. It should be noted that areas of values of complex speed in the specified cases allow to apply by means of inversion at a solution Christoffel-Schwartz’s formula.

In work the exact analytical solution of a task on a current of subsoil waters in a rectangular jumper with slopes of A0A1 and D0B, width of L located on the impenetrable horizontal basis of length of L is given. Water height is equal in an upper bye to H, lower reach with water level of H2, having partially impenetrable vertical wall CD (screen), adjoins a basis sole. The upper bound of area of the movement is free pover khnost AD which is coming out with which there is a uniform evaporation to intensity ε (Figure 2). In the considered area of complex speed, unlike [2,6,7,17,18], there are not rectilinear, but circular polygons that does not give the chance to use classical integral of Christoffel-Schwartz.

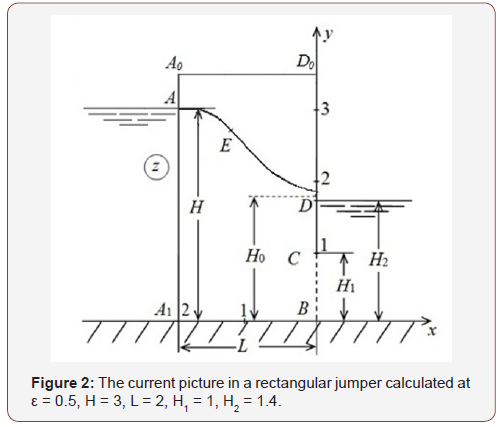
The task solution on a current to the imperfect well formally turns out from a task solution on filtering in a rectangular jumper with partially impenetrable vertical wall in case of its infinite width, i.e. at L = ∞ [19,20].

For studying of the specified currents in the presence of evaporation or infiltration on a free surface the mixed multiple parameter boundary value problem of the theory of analytic functions which solution is carried out with use of the method of P.Ya. Polubarinova-Kochina [2-7] based on application of the analytical theory of linear differential equations of a class of Fuchs are formulated. And also [21-23] ways of conformal mapping of a special type of circular polygons [24] developed for areas which are very typical for tasks of the theory of filtering. Accounting of characteristics of the considered classes of areas of the hodograph of speed allowed to present solutions of tasks in the closed form through elementary functions that does their use the simplest and convenient in practice.

On the basis of the studied model’s calculation algorithms are developed:

• heights of a raising of a subsoil water behind Zhukovsky’s groove at it obteka6nii, width of capillary spreading of liquid on a water emphasis (in scheme 1) and also values of a filtration expense;

• ordinates of exit point of a curve depression on the screen, a filtration expense and coordinates of points of a free surface when filtering in a rectangular jumper and to imperfect gallery.

• The received results give an idea (at least qualitatively) of possible dependence of characteristics of a current by filtering consideration already to the imperfect well or a tubular well.

None.

No conflict of interest.

1. NE Zhukovsky (1950) Leakage of water through dams. Gostekhizdat 7: 297-332.
2. P Ya Polubarinova Kochina (1952) Theory of the movement of subsoil waters. Gostekhizdat. 676 pages; the 2nd prod. Science, 1977, 664 pages.
3. VI Aravin, SN Numerov (1953) The theory of the movement of liquids and gases in the non-deformable porous environment. Gostekhizdat, 616 pages.
4. (1967) Development of researches on the theory of filtering in the USSR (1917–1967). 545 pages.
5. GK Mikhaylov, VN Nikolayevsky (1970) The movement of liquids and gases in porous environments. Mechanics in the USSR in 50 years, Science 2: 585-648.
6. P Ya Kochina (1991) Chosen works. Hydrodynamics and theory of filtering. Science, 351 pages.
7. P Ya Polubarinova Kochina, VG Pryazhinskaya, VN Emikh (1969) Mathematical methods in questions of irrigation –Science.
8. EN Bereslavskii (2013) About some hydrodynamic models connected with a problem of Zhukovsky about flow of a groove. Dokl RAS 448(5): 529-533.
9. EN Bereslavskii (2014) About some mathematical models connected with a problem of Zhukovsky about flow of a groove. Applied mathematics and mechanics 78(3): 394-400.
10. EN Bereslavskii (2017) Modeling the Movement of Groundwater from the Pits, Surrounded with Tongues of Zhukovsky. International Journal of Teoretical and Applied Mathematics (USA)3(4): 124-137.
11. EN Bereslavskii (2017) Effect of Evaporation or Infiltration on the Free Surface of Groundwater in Certain Problems of Underground Hydromechanics. American Journal of Applied Mathematics and Statictics 5(5): 159-163.
12. EN Bereslavskii (2017) Application of Method Polubarinova-Kochina for Research of Groundwater Motion from Ditcheshences Tongue Zhukovsky. International Journal of Mathematical Sciences: Advance and Applications 8(1): 11-28.
13. VG Pryazhinskaya (1964) The movement of subsoil waters in a rectangular jumper with an impenetrable vertical wall. Izv Academy of Sciences of the USSR. Mechanics and mechanical engineering 2: 41-49.
14. P Ya Polubarinova Kochina, VA Postnov, VN Emikh (1967) The established filtering to imperfect gallery in non-pressure layer. Izv Academy of Sciences of the USSR. Mechanics of liquid and gas 4: 97-100.
15. EN Bereslavskii, LM Dudina (2018) About the movement of subsoil waters to imperfect gallery in the presence of evaporation from a free surface. Mathematical modeling 30(2): 99-109.
16. EN Bereslavskii, LM Dudina (2018) On Ground Water Flow to an Imperfect Gallery: Case of Evaporation from a Free Surface. Mathematical Models and Computer Simulations 10(5): 601-608.
17. EN Bereslavskii, P Ya Kochina (1992) About some equations of a class of Fuchs in gidro-and aeromechanics. Izv RAS Mechanics of liquid and gas 5: 3-7.
18. P Ya Kochina, EN Bereslavskii, NN Kochina (1996) Analytical theory of linear differential equations of a class of Fuchs and some problems of underground hydromechanics. Ying t of mechanics problems RAS Preprint 567: 1-122.
19. EN Bereslavskii, P Ya Kochina (1997) About the differential equations of a class of Fuchs which are found in some problems of mechanics of liquids and gases. Izv RAS Mechanics of liquid and gas 5: 9-17.
20. EN Bereslavskii (1997) About the differential equations of a class of Fuchs connected with conformal mapping of circular polygons in polar grids. Differential equations 33(3): 296-301.
21. EN Bereslavskii (2009) About integration in the closed form of some differential equations of a class of Fuchs which are found in gidro-and aeromechanics. Dokl RAS 428(4): 439-443.
22. EN Bereslavskii (2010) About accounting of infiltration or evaporation from a free surface by method of circular polygons. Applied mathematics and mechanics 74(2): 239-251
23. EN Bereslavskii (2010) About integration in the closed form of some differential equations of a class of Fuchs connected with conformal mapping of circular pentagons with a section. Differential equations 46(4): 459-466.
24. EN Bereslavskii (2013) About application of the equations of a class of Fuchs for calculation of filtering from channels and sprinklers. Applied mathematics and mechanics 77(5): 711-724.