Using AMRO Quantum Oscillations to Probe the Fermi Surface of Quasi-2d Layered Organic Conductors in Low Temperatures and High Magnetic Fields

Organic materials are generally synthesized as single crystals with alternating organic-inorganic layers. This induces a reduced dimensionality, leading to a Quasi-two-dimensional (Q2D) salt, having higher conductivity along the crystal plane. This accounts for the ratio of the inter-plane to in-plane resistance reaching upward to an order of a thousand. The electrical anisotropy is seen at Room Temperature and with temperature change and in the presence of a magnetic field which shows up in magnetoresistance (MR), the sample’s resistance response to a magnetic field. By orienting the sample with respect to the magnetic field, we can study the electrical anisotropy evidenced by quantum oscillations in the resistance in the form of Shubnikov-de Haas (SdH) and angular-dependent magnetoresistance oscillations (AMRO). The differences between the two are: SdH measurements display oscillations at fixed temperature and angle as the magnetic field is swept; whereas, AMRO is observed at fixed temperature and magnetic field as the orientation of the sample (angle) is changed. The AMRO angular changes are two types: polar (θ) and azimuthal (φ). The polar angle θ is defined as the angle between the magnetic field and the normal to the two-dimensional organic cation layer, while the azimuthal angle φ is the direction of the magnetic field’s rotation relative to the a-b plane. With SdH oscillatory data, we can extract meaningful information such as the: effective mass, Dingle temperature, frequency of the electron orbits and FS areas. AMRO data analysis leads to direct probing of the FS surface where we can quantify the Fermi wave vector (kf) and map the shape and warping (if present) of the FS and compare it with predictions from band structure calculations. Of note is the magnetic analog of SdH which is de Haas-van Alphen oscillations which shows up as oscillations in the magnetization. The treatment of these oscillations uses Lifshitz- Kosevich Theory [2,3], which when applied to SdH oscillations is extremely effective. In this paper, we will discuss AMRO oscillations and the formalism of their analysis by measuring the interlayer magnetoresistance in a tilted magnetic field at fixed temperatures. We will provide an example of past data for clarity of our discussion [1].

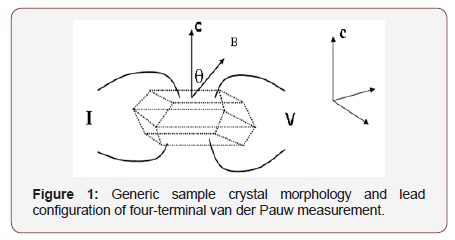
Q2D organic conductors were first observed to display angular dependent magnetoresistance oscillations (AMRO) [4]. However, layered oxides [5] and semiconductor super lattices [6] have also had AMRO detected in them. Anisotropy in layered organic conductors permits resistivity measurements in both the in-plane and inter-plane configuration. Measurements are taken using an AC 4-terminal van der Pauw configuration (using 10micron gold wire attached with silver or carbon paint) as shown (Figure 1). Currents typically up to 10 (high currents can induce self-heating) and frequencies below 100Hz (avoiding frequencies close and equal to 60Hz) are applied and the resulting voltage is read across the other two terminals. The current and voltage along with sample’s dimensions gives us the resistivity of the sample. Note that the current passes along the c axis, this represents inter-plane electrical transport.

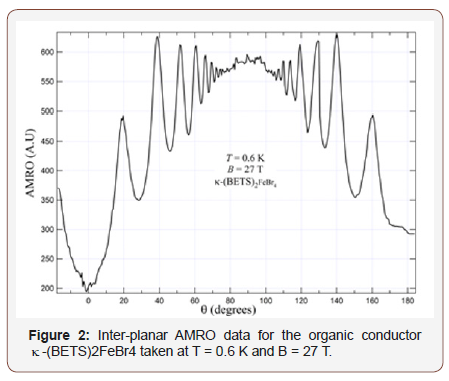
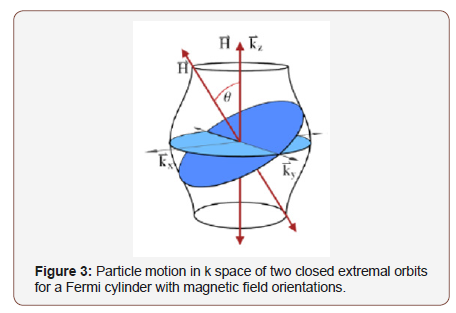
(Figure 2) is a sample of AMRO inter-plane resistance data taken on the organic conductor κ-(BETS)₂FeBr₄ for an unspecified φ angle at T = 0.6 K and B = 27 T. The inter-plane MR oscillates with defined peaks and valleys. The angles at which the peaks occur are called magic angles which are indexed as q_n. The significance is that these magic angles correspond to 2-D closed orbits where the FS has the same area, this causes warping of the fermi cylinder producing necks and bellies (Figure 3). The pronounced amplitudes of the oscillations stem from all electrons in the highest occupied Landau levels contributing to the oscillatory effect. The area associated with the cyclotron motion was calculated by Yamaji [8] and is given in equation 1, where kF is the Fermi wave number, Jo is the zeroth order Bessel function and c is the layer spacing.

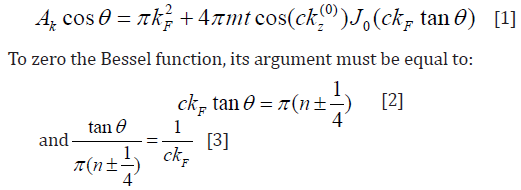
Equation 3 shows us that the AMRO data will be periodic in tanθ; so, we plot the data w.r.t. tanθ which shows good periodicity (Figure 4). The peaks are then indexed “n” and plotted against 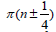, the slope of which is equal to 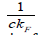(Figure 5). Also, we can calculate Dtanθ for each successive pair of peaks, where Dtanθ gives the Fermi wave vector as:

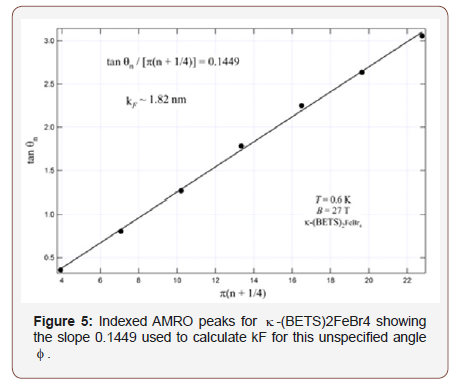
Using the slope from Figure 5 and c the interlayer spacing we calculate k_F = 0.182 Å for the unspecified angle φ. Recall kF is dependent on φ, therefore with each change of the azimuthal angle, we obtain another k_F. Collectively we obtain an in-plane mapping of the Fermi momentum [9].

Our review gives a concise application of AMRO measurements and analysis for detailed study of the FS of layered Q2d materials at low temperatures and high magnetic fields. We used previously reported κ-(BETS)₂FeBr₄ data as an example of achieving a single Fermi momentum for an arbitrary azimuthal angle φ. Analysis of the theory confirms a 2D corrugated Fermi surface based on AMRO observation and k_F = 0.182 Å.

The author acknowledges James Brooks, Luis Balicas, D. Graf, S. Uji, H. Shinagawa, E. Ojima, H. Fujiwara, H. Kobayashi, A. Kobayashi, M. Tokumoto. A portion of this work was performed at the National High Magnetic Field Laboratory (NHMFL), which is supported by National Science Foundation Cooperative Agreements No. Division of Materials Research 1157490 and No. Division of Materials Research 1644779 and the State of Florida.

No conflict of interest.

1. Balicas L, Brooks JS, Storr K, Graf D, Uji S, et. al. (2000) Shubnikov–de Haas effect and Yamaji oscillations in the antiferromagnetically ordered organic superconductor κ-(BETS)2FeBr4: a fermiology study, Solid State Communications 116(10): 557-562
2. Shoenberg D (1984) Magnetic Oscillations in Metals. Cambridge University Press, UK, pp.22-82.
3. Lifshitz IM, Kosevich AM (1955) On the Theory of Magnetic Susceptibility of Metals at Low temperatures. Zh eksp teor fiz 29(6): 730.
4. Kartsovnik MV, Kononovich PA, Laukhin VN, Schegolev IF (1988) Anisotropy of magnetoresistance and the Shubnikov-de Haas oscillations in the organic metal β-(ET)2IBr2. Journal of Experimental and Theoretical Physics Letters 48: 541.
5. Ohmichi E, Adachi H, Mori Y, Maeno Y, Ishiguro T, et. al. (1999) Angledependent magnetoresistance oscillation in the layered perovskite Sr2RuO4. Physical Review B 59(11): 7263-7265.
6. Yagi R, Iye Y, Osada T, Kagoshima S (1990) Semiclassical Interpretation of the Angular-Dependent Oscillatory Magnetoresistance in Quasi-Two- Dimensional Systems. J Phys Soc Jpn 59: 3069-3072.
7. Norman M (2010) Trend: Fermi-surface reconstruction and the origin of high-temperature superconductivity. Physics 3: 86.
8. Yamaji K (1987) On the Small-Period Oscillation of Magnetoresistance in the Bechgaard Salts. J Phys Soc Jpn 56: 1101-1110.
9. Kajita K, Nishino Y, Takahashi T, Kato R, Kobayashi H, et. al. (1989) A New Type Oscillatory Phenomenon in the Magnetotransport of Ɵ-(BEDTTTF) 2 I3. Solid State Communications 70(12): 1189.