 Review Article
Review Article
Experimental Verification of the Mechanical State Equation Adequacy for Description of the Creep of Some Polymer Materials under Non-stationary Modes of Static and Cyclic Loading in Plain Stress
Leonid Ogorodov1, Sergey Krasikov2, Inna Nikolaeva3*
1,3St. Petersburg State Polytechnical University, Polytechnicheskaya Str. 29, St. Petersburg, Russia
2CJSC Vologda Timber Chemical Plant, Rosin station, Vologda, Russia
Inna Nikolaeva, St. Petersburg State Polytechnical University, Polytechnicheskaya Str. 29, 195251, St. Petersburg, Russia.
Received Date: June 20, 2022; Published Date: July 05, 2022
Abstract
The equation of mechanical condition for the description of deformation of polymer and polymer composite materials under complex modes of long static and cyclic loading in condition of the plain stress state is developed. The experimental data show its efficiency. The means of accounting the influence of natural aging and the damage accumulation data of a material are suggested. The opportunity of using of a simplified variants of the equation is shown.
Keywords: Creep; Polymer materials; Mechanical state equation; Complex modes of loading; Experimental test
Introduction
Polymer and composite polymer materials proved an important class of structural materials with rheonomous properties. A variety of approaches to evaluation of the deformation of these materials and the time to failure can be found in the literature [1]. In general case the total strain under continuous loading is defined by the sum of four components: instantaneous-elastic, instantaneous -plastic, visco-elastic, and visco-plastic [2]:
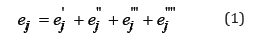
The components of the total strain deviator (Eq.1) are represented as:2
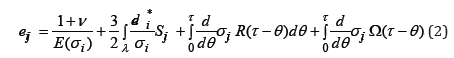
or as:
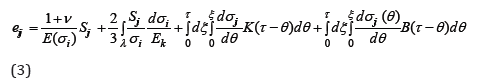
where Sj is the deviatorial stress components; 𝝂 is the Poisson’s
ratio; E – modulus of elasticity (in general case the non-linear
elasticity should be considered); is the von-Mises equivalent
stress, 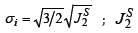 is the second invariant of deviatorial stress;
is the second invariant of deviatorial stress; 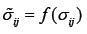 are the components of a characteristic stress;
K(τ −θ ) and R(τ −θ ) are the cores of after action τ −θ =ξ is
the time (it can be actual or dimensionless time); Ω(τ −θ ) and
B(τ −θ ) are the time functions; * i de is the equivalent strain increment,
are the components of a characteristic stress;
K(τ −θ ) and R(τ −θ ) are the cores of after action τ −θ =ξ is
the time (it can be actual or dimensionless time); Ω(τ −θ ) and
B(τ −θ ) are the time functions; * i de is the equivalent strain increment, 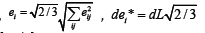 Ek is the tangential modulus,
Ek is the tangential modulus, 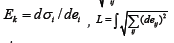 is the plastic strain path, Odlvist’s parameter.
is the plastic strain path, Odlvist’s parameter.
For calculation of the relative change of a unit volume we suggest using a characteristic strain:
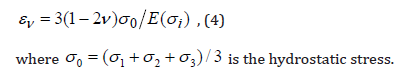
The non-linear law of instantaneous elasticity was defined in testing materials at fast (instant) unloading of specimen from the given level of stress attained at a high enough rate. To find out the dependence of instantaneous plastic component of the total strain on the stress the same tests were used, but the residual strains were measured after unloading and after holding a certain time in unloading. The instantaneous plastic strain component can be taken into account within the range of the visco-plastic component.
In description of the rheonomous components of the total strain the processes of shear are considered on condition of the volume stability of material. The visco-elastic component of strain is determined as:
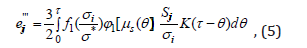
where s μ is the Lode’s factor, σ * is the dimensional constant. The function ϕ has to be obtained by testing specimens at the complex stress state.
To define the visco-plastic strain component '''' eij is necessary to deduce (during the whole period of stationary mode of loading) the appropriate instantaneous and visco-elastic components from the total strain it. The visco-plastic component is described as follows from [3 – 4]:
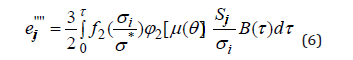
The calculation of strain components according to (2) and (3) at any unsteady loading condition and known constants is reduced to quadratures. The evaluation of the loading regime relative to the specified path of deformation (the stress relaxation under constant deformations should be considered as well) is carried by applying the step-by-step procedure in a general case. The constant and functional parameters of equations of mechanical state of polymer composite materials essentially depend on temperature. Methods of testing equipment and characteristics of the samples are presented in [1-13]. If only temporal parameters of the equation depend on temperature, then under some additional conditions the temperature-temporary analogy may be established, on which the process of no isothermal loading is reduced to the isothermal one within the given time. Within the range of physical nonlinearity of material on the temperature depend not only temporal, but also the force parameters of equations (2) and (3).
In such cases a method of transformation of a stepwise non isothermal mode of loading to an equivalent isothermal mode is developed. The finite magnitudes of visco-elastic and visco-plastic components of the total strain are obtained by superposition of a series of loading impulses applied at actual or reduced moments of time.
The natural aging (aging time τc ) and damage (Π) under continuous loading affect the process of creep of material and the ultimate strain [14]. The accumulated strains and damages change the relationship between the components of the total strain at step-wise loading regimes (with partial or complete intermediate unloading). At long pauses after loading a number of concurrent processes develops in material, in particular, damage remedies and natural aging. Equations (2), (3) contain functional parameters (depending on τc and Π) [15], which should be obtained by analysing the additional tests results. The account for the damage measure П appears effective only by the description of strains directly preceding the moment of failure.
The obvious may be the application of the suggested equation of the mechanical states to the conditions of the cyclic stress state [16]. The instantaneous components of the total strain are calculated considering the maximal ones through the stress cycle. The viscoelastic component can be calculated directly by substituting the variable stress. A number of approaches is suggested for calculation of the visco-plastic strain component [4]. The possibility of application of the simplified variant of the equation of mechanical states was considered. The process of deformation (creep) of tubular specimens of aged polyethylene (14 years) under various regimes of stationary and non-stationary loading by axial tensile load, internal pressure and torque may be described with sufficient accuracy by the accounting for the instantaneous elastic and rheonomous components of the total strain:
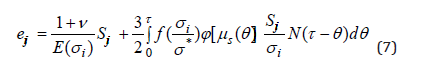
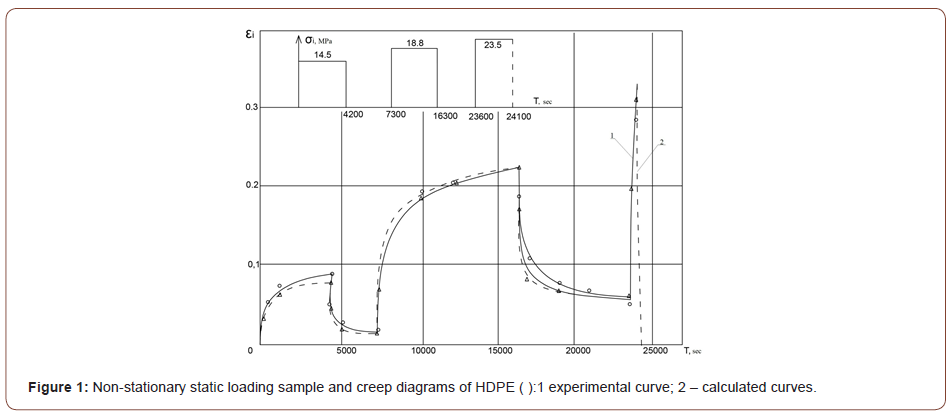
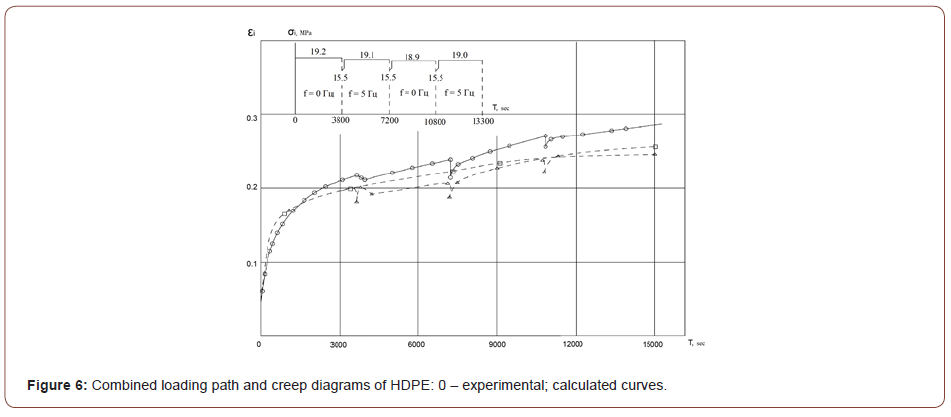
The calculated strains deviate from the experimentally obtained ones by 20%, and under the loading conditions without torque the difference does not exceed 13%. The examples of experimental and calculated creep diagrams are given in Figures 1-6. The figures show the qualitative and quantitative differences between experimental creep curves and analysis (description) of figures is not necessary (Figures 1-6).
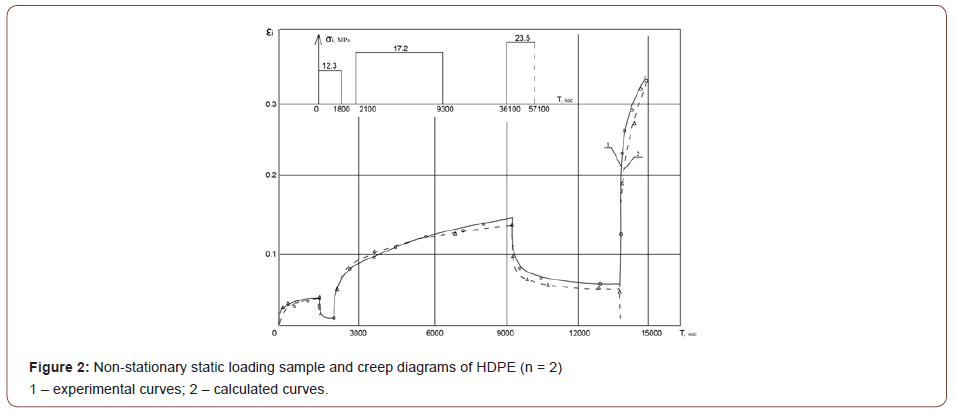
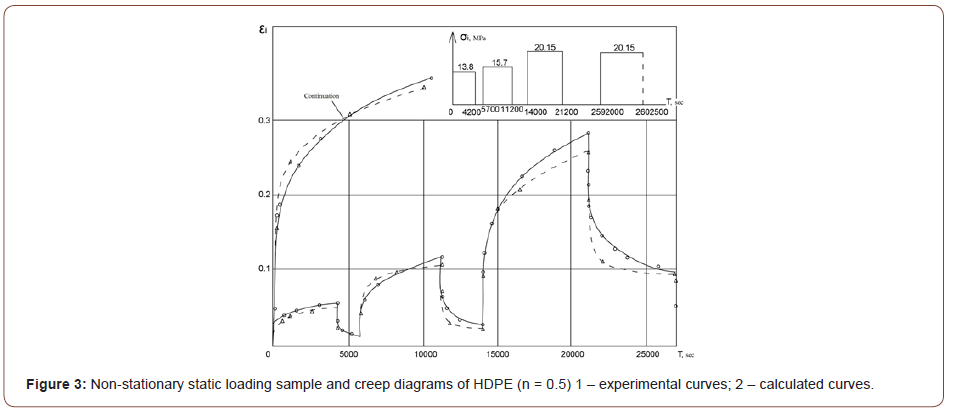
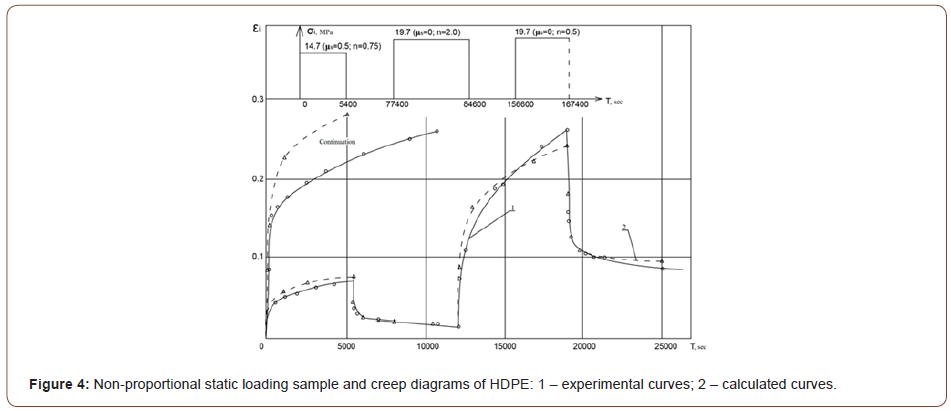
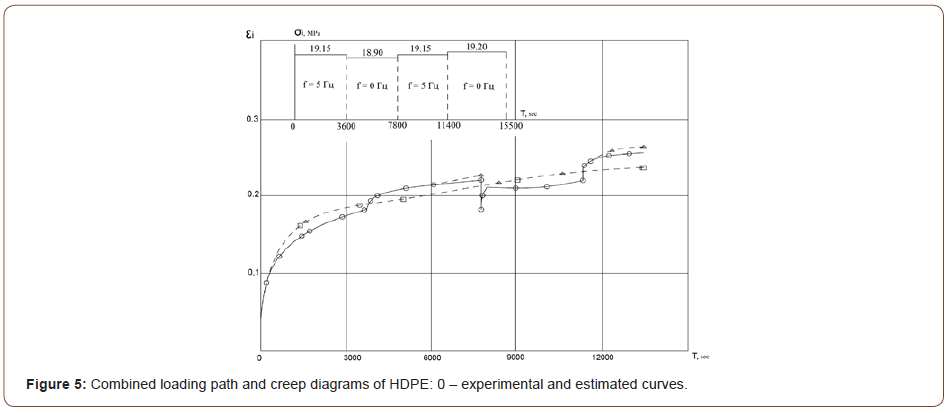
Summary
The above conclusions also can be extended on the cases of cyclic alteration of all or any one stress component. However, it is indicative that despite of nonlinearity of the genetic stress equation, the evaluation of strain components can be carried out considering the average stress magnitudes over the loading cycle. Analysis [17] shows that the rigorous account of the cyclic stress variation results in insignificant refinement of strain components [18–21]. In this paper above equations are applicable to a class of semi-crystalline polymeric materials such as low-density polyethylene, PVC and PTFE 4 and 4D [22–25].
Acknowledgment
None.
Conflict of Interest
No conflict of interest.
References
- Pavlov PA (1988) Basics of engineering calculation of machine elements of fatigue and long-term strength. Basics of engineering calculation of machine elements of fatigue and long-term strength, p.252 (Russia).
- Aybinder SB, Tyunina EL, Tsirule KI (1981) Properties of polymers in different states of stress. Properties of polymers in different states of stress, p.232 (Russia).
- Bugakov II (1973) Creep of Polymeric Materials. Creep of Polymeric Materials, p.288 (Russia).
- Pavlov PA, Ogorodov LI (1998) The study of the ultimate strain of polycrystalline polymeric materials under static and cyclic loading. Plasticheskie massy, 11: 27-29 (Russia).
- Bartenev GI (1984) Strength and fracture mechanisms of polymers. Strength and fracture mechanisms of polymers, p.280 (Russia).
- Goldman A Ya (1979) The strength of engineering plastics. The strength of engineering plastics, p.320 (Russia).
- Pavlov PA, Ogorodov LI (1991) Long term resistance of materials with hereditary properties. Dlitelnoye soprotivleniye konstruktsionnykh materialov i voprosy rascheta elementov konstruktsiy, pp. 4-10 (Russia).
- Pavlov PA, Ogorodov LI (1991) Long term resistance of thermoplastics under thermomechanical loading with natural aging. Collection VNTO a name of academician AN Krylov, 510: 15-23 (Russia).
- Pavlov PA, Ogorodov LI (1991) Long term resistance of polymeric and composite materials with a time of long-term natural aging. Mechanics of Composite Materials, 4: 692-696 (Russia).
- Belan-Gayka VN, Ogorodov LI (2012) Geometrical similarity of the stress deviator and the strain rate of creep of polymeric materials in the linear and cyclic proportsionnalnogo complex loading conditions. Materialy desyatoy vserossiyskoy konferentsii: Vuzovskaya nauka – region, pp.135-139 (Russia).
- Ogorodov LI, Ogorodova IL (2007) Mathematical model of information processes with rheonomic properties about complex modes sustained loading. Materials of the fourth international scientific and technical conference, pp.141-144 (Russia).
- Ogorodov LI, Kotyagov LF, Kurilovich NN (2006) Deformation of polycrystalline polymeric materials in terms of short-term load. Materialy tretyey Belorusskoy nauchno-prakticheskoy konferentsii, pp. 329-333 (Russia).
- Sherstnev VA, Goldman Aya (1976) Installation for testing of polymeric materials fatigue in a plane stress. Problemy prochnosti, 12: 111-113 (Russia).
- Kastner M, Obst M, Jorg B, Karin T, Volker U (2012) Inelastic material behavior of polymers – Experimental characterization, formulation and implementation of material model. Mechanics of Materials, 52: 40-57.
- Melnikov BE, Semenov AS (2014) Fatigue damage accumulation under the complex varying loading. Applied Mechanics and Materials, 617: 187-192.
- Semenov AS, Melnikov BE, Gorokhov MY (2005) About the causes of cyclical instability at computations of large elasto-plastic strains. Proceedings of SPIE – The International Society for Optical Engineering, 25: 167-173.
- Semenov AS, Sahn S, Melnikov BE (2001) Comparison of fatigue life prediction on the base of straight and zigzag-like cracks models. Proceedings of SPIE – The international Society for Optical Engineering, 4348: 312-321.
- Stalevich AM, Kikets EV, Stolyarov ON, Saidov ED (2003) Effect of the Relaxation Modulus on the Shape of the Stress and Strain Diagram of an Oriented Amorphous-Crystalline Polymer. Fiber Chemistry, 35(2): 164-167.
- Zhukovski VA, Makarov AG, Rostovtseva NG, Slutsker GY, Stolyarov ON, et.al. (2003) Deformation behavior of medical synthetic monofilaments. Fiber Chemistry, 40(4): 318-321.
- Benin AV, Semenov AS, Semenov SG, Melnikov BE (2013) Mathematical modeling of bond failure of reinforcement with concrete. Part 1: Models with the discontinuity connection. Magazine of Civil Engineering, 5 (40): 86-99 (Russia).
- Neklyudova EA, Semenov AS, Melnikov BE, Semenov SG (2014) Experimental study and finite element analysis of elastic and strength properties of glass fiber composite material. Magazine of Civil Engineering, 3 (47): 25–40.
- Pavlov PA, Andreev AV (1976) Investigation of creep PTFE-4 in a planar cyclic stress state. Mekhanika polimerov, 6: 1099-1103 (Russia).
- Pavlov PA, Kondakova ON, Belan-Gayko VN (1980) Polyethylene creep under complex stress state in a non-stationary loading. Mekhanika kompozitnykh materialov, 5: 793-801 (Russia).
- Pavlov PA, Krutskikh NA (1984) Phenomenological description and experimental study of deformation processes in complex thermomechanical loading semi-crystalline materials. Mekhanika kompozitnykh materialov, 6: 974-979 (Russia).
- Pavlov PA, Yakovleva EL, Krutskikh NA (1983) Analytical description of deformation and fracture of structural elements made of polymeric materials. Trudy LPI, 393: 3-7 (Russia).
-
Leonid Ogorodov, Sergey Krasikov, Inna Nikolaeva*. Experimental Verification of the Mechanical State Equation Adequacy for Description of the Creep of Some Polymer Materials under Non-stationary Modes of Static and Cyclic Loading in Plain Stress. Cur Trends Civil & Struct Eng. 9(1): 2022. CTCSE.MS.ID.000701. DOI: 10.33552/CTCSE.2022.09.000701.
-
Creep, Polymer materials, Mechanical state equation, Complex modes of loading, Experimental test
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






