The r_T − X Family of Distributions induced by V: A New Method for Generating Continuous Distributions with Illustration to Cancer Patients Data

At first we recall the q_T − X (V) framework which is inspired by [1] and [2]

Definition 3.1. Let V be any function such that the following holds:

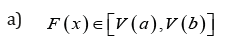
b) F (x) is differentiable and strictly increasing

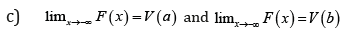
then the CDF of the q_T − X (V) family induced by V is given by

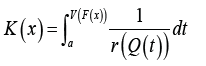
where 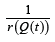is the quantile density function of random variable T ∈ [a,b] , for −∞ ≤ a < b ≤ ∞, and F (x) is the CDF of any random variable X.

Theorem 3.2. The CDF of the q_T − X family induced by V is given by

K ( x) = Q[V (F ( x))]

Proof. Follows from the previous definition and noting that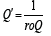

Theorem 3.3. The PDF of the qT − X family induced by V is given by

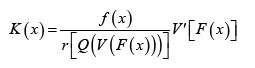
Proof. 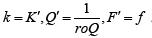and K is given by Theorem 3.5.2

Remark 3.4. When the support of T is[a,∞), where a ≥ 0 , we can take V as follows

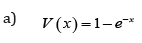
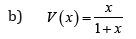
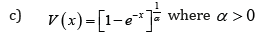where α > 0

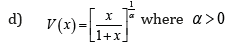where α < 0

Remark 3.5. When the support of T is (−∞,∞) , we can take V as follows

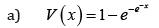
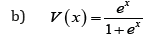
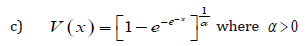where α > 0

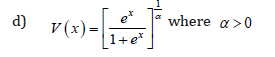where α > 0

Suppose a random variable T has quantile function Q, quantile density q, CDF R, and PDF r, then since

Q = R⁻¹

The following is clear

Q(R(t )) = t and R(Q(t )) = t

If we differentiate both sides of, R(Q(t )) = t , with respect to t and solve for q(t), we get the integrand in Definition 4.1. On the other hand, if

we differentiate both sides of, Q(R(t )) = t ,with respect to t, and solve for r(t), we can see that 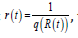thus making this replacement to the integrand

in Definition 1.1 leads to the following

Definition 4.1. Let V be any function such that the following holds:

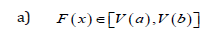
b) F (x) is differentiable and strictly increasing

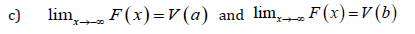
then the CDF of the r_T − X family induced by V is given by

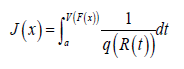
where 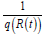is the probability density function of random variable T ∈[a,b] , for ] −∞ ≤ a < b < ∞, and F(x) is the CDF of any random variable X.

Notation 4.2. Ψ will denote the class of all functions V satisfying (a), (b), and (c) in the definition immediately above

Since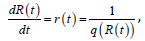 implies the following

Theorem 5.1. The CDF of the Tr − X family induced by V is given by

J ( x) = R(V (F ( x)))

where the random variable T ∈[a,b] , for −∞ ≤ a < b < ∞, has CDF R,V ∈Ψ , and F(x) is the CDF of any random variable X.

By differentiating the CDF in Theorem 5.1, with respect to x, we have the following

Theorem 6.1. The PDF of the T_r − X family induced by V is given by

j ( x) = r (V (F ( x)))V′(F ( x)) f ( x)

where the random variable T ∈[a,b] , for −∞ ≤ a < b < ∞, has PDF r,V ∈Ψ, F (x) and f(x) are the CDF and PDF, respectively, of any random variable X.

At first we introduce the following

Definition 7.1. A random variable K will be said to follow the new T_r − X family of distributions of type I, if the CDF can be expressed as the following integral

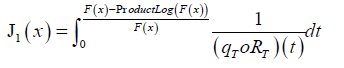
where the random variable X has CDF F(x), and the random variable T with support [0,∞) has quantile density qT and CDF RT, and Product Log [z] gives the principal solution for w in z = we^w

Remark 7.2. Note that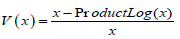 is our weight in the above definition, and

V⁻¹ gives 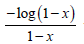which is the weight function introduced in [3]

Since 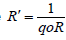which is the weight function introduced, then the above definition implies the following

Theorem 7.3. The CDF of the new T_r − X family of distributions of type I is given by

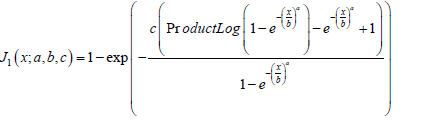
where the random variable T with support [0,1) has CDF RT, Product Log[z] gives the principal solution for w in z = we^w , and the random variable X has CDF F(x)

Remark 7.4. By differentiating the CDF above, the PDF of the new T_r − X family of distributions of type I can be obtained

By assuming 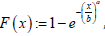, that is, X is Weibull distributed and 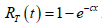, that is, T is exponentially distributed. We get the following from Theorem 7.3

Theorem 7.5. The CDF of the new Exponential-Weibull family of distributions of type I is given by

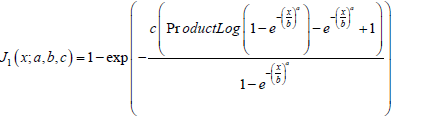
where a, b, c, x > 0, and Product Log[z] gives the principal solution for w in z = we_w

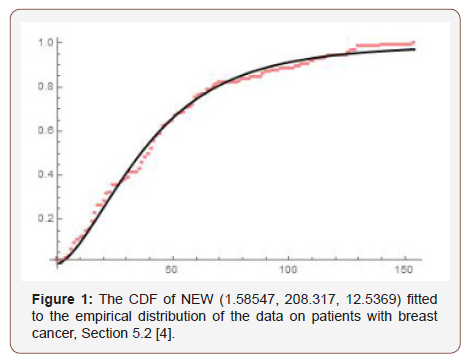
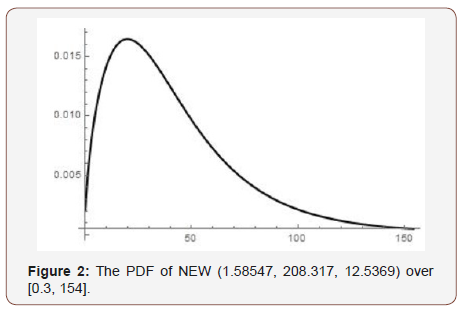
Remark 7.7. The PDF of the new Exponential-Weibull family of distributions of type I can be obtained by differentiating the CDF above.

None.

No conflict of interest.

1. Clement Ampadu (2013) Results in Distribution Theory and Its Applications Inspired by Quantile Generated Probability Distributions, Lulu.com. ISBN: 0359249957,9780359249954.
2. Clement Boateng Ampadu (2018) Quantile-Generated Family of Distributions: A New Method for Generating Continuous Distributions. Fundamental Journal of Mathematics and Mathematical Sciences 9(1): 13-34.
3. Zubair Ahmad, M Elgarhy, GG Hamedani (2018) A new Weibull-X family of distributions: properties, characterizations and applications. Journal of Statistical Distributions and Applications 5:5
4. Girish Babu Moolath, Jayakumar K (2017) T-Transmuted X Family of Distributions, STATISTICA, anno LXXVII, n. 3.