 Review Article
Review Article
The Ampadu APT − qT − X Family of Distributions Induced by V with an Illustration to Data in the Health Sciences
Clement Boateng Ampadu, Department of Mathematics, USA.
Received Date: March 05, 2019; Published Date: March 26, 2019
Abstract
The alpha power transform family of distributions ( APT −G for short) appeared in [1], and since then variants of it has been
proposed, and for example, see [2]. In this paper we propose another variant of the APT −G family of distributions called the Ampadu
APT −G family of distributions. Assuming G is given by the CDF of qT − X family of distributions induced by V , and for example, see [3] and [4], we show sub-models of the Ampadu APT − qT − X (V) family of distributions is significant in modeling data in the health sciences, in particular, the breast cancer patients data contained in [5]. As a further development of the APT −G family of distributions, we propose a so-called 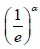 power transform family of distributions (
power transform family of distributions (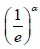 PT-G for short).
PT-G for short).
Keywords: Alpha power transform; Ampadu-G; Quantile generated family of distributions
Background on qT −X Family of Distributions Induced by V
This section is inspired by [3] and [4]
Definition 3.1. Let V be any function such that the following holds:
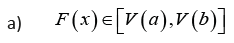
b) F (x) is differentiable and strictly increasing
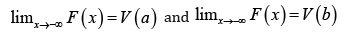 then the CDF of the qT − X family induced by V is given by
then the CDF of the qT − X family induced by V is given by
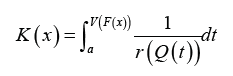
where 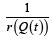 is the quantile density function of random variable
T ∈ [a,b] , for −∞ ≤ a < b ≤ ∞, and F (x) is the CDF of any random
variable X.
is the quantile density function of random variable
T ∈ [a,b] , for −∞ ≤ a < b ≤ ∞, and F (x) is the CDF of any random
variable X.
Theorem 3.2. The CDF of the qT − X family induced by V is given by
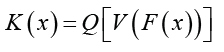
Proof. Follows from the previous definition and noting that 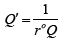
Theorem 3.3. The PDF of the qT − X family induced by V is given by
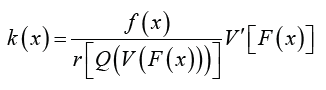
Proof. 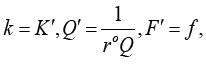 and K is given by Theorem 3.5.2
and K is given by Theorem 3.5.2
Remark 3.4. When the support of T is[a,∞), where a ≥ 0 , we can take V as follows
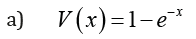
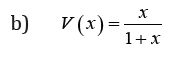
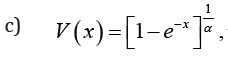 where α > 0
where α > 0
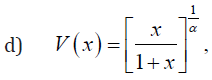 where α < 0
where α < 0
Remark 3.5. When the support of T is (−∞,∞) , we can take V as follows
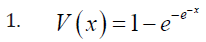
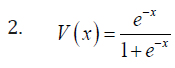
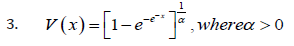 where α > 0
where α > 0
 where α > 0
where α > 0
The New Family of Distributions
The Ampadu APT-G aamily of distributions
Definition 4.1. A random variable X will be called Ampadu APT-G distributed if the
CDF is given by
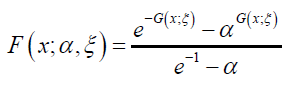
and the PDF is given by
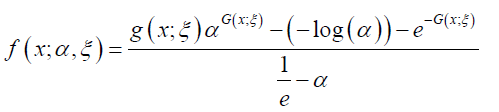
Where 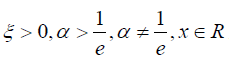 ,and G is some baseline
distribution.
,and G is some baseline
distribution.
Application to the qT − X family of distributions induced by V
Definition 4.2. A random variable J1 will be called Ampadu APT − qT − X distributed of type I if the CDF is given by
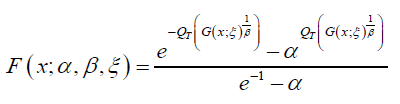
Where 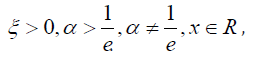 G is some baseline distribution associated with the
G is some baseline distribution associated with the
random variable X, β > 0 , and the random variable T with support [0, 1] has quantile QT
Remark 4.3. The PDF can be obtained by differentiating the CDF above
Definition 4.4. A random variable J2 will be called Ampadu APT − qT − X distributed of type II if the CDF is given either by
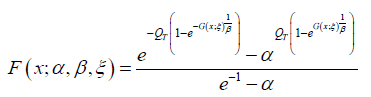
Or

where 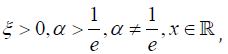 G is some baseline distribution associated with the random variable X, β > 0 , and the
random variable T with support [0,1] has quantile QT
G is some baseline distribution associated with the random variable X, β > 0 , and the
random variable T with support [0,1] has quantile QT
Remark 4.5. The PDF can be obtained by differentiating the CDF immediately above
Definition 4.6. A random variable J3 will be called Ampadu APT − qT − X distributed
of type III if the CDF is given either by
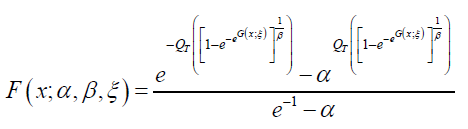
Or
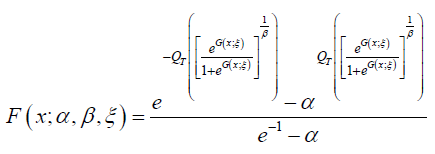
where  G is some baseline distribution
associated with the
G is some baseline distribution
associated with the
random varaible X, β > 0 , and the random variable T with support (−∞,∞) has quantileQT
Remark 4.7. The PDF can be obtained by differentiating the CDF immediately above
An Illustration to Breast Cancer Patients Data
Application of Definition 4.2
We assume β =1, T is uniform on [0, 1], and the random variable X follows the Weibull distribution, so that the CDF of X is given by
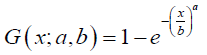
and the PDF of X is given by
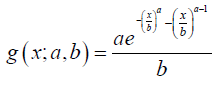
Now from Definition 4.2, we have the following
Theorem 5.1. The CDF of the Ampadu APT-{Quantile Uniform- Weibull} distribution of type I is given by
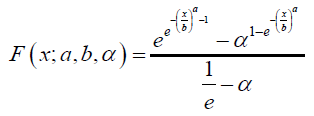
Where 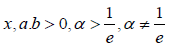
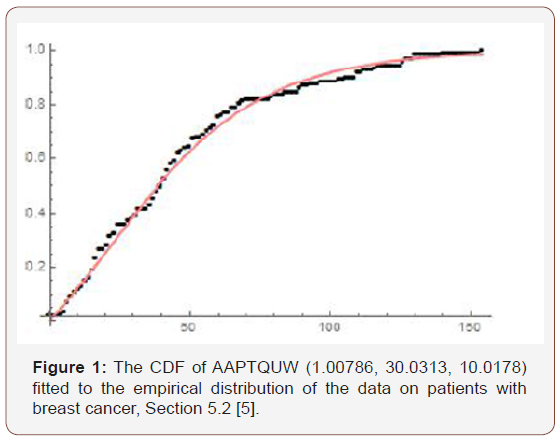
Remark 5.2. If a random variable B (say) has CDF given by the previous theorem we Write B ~ AAPTQCW(a,b,α ) (Figure 1)
By differentiating the CDF given by Theorem 5.1, we get the following
Theorem 5.3. The PDF of the Ampadu APT-{Quantile Uniform- Weibull} distribution
of type I is given by
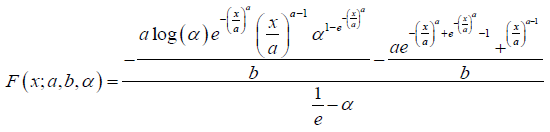
Where 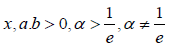 (Figure 2)
(Figure 2)
Application of definition 4.4
We assume T is a fully specified exponential distribution. In particular, we assume T has CDF
1− e−0.714286t
so that the quantile of T in this case is given by
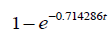
We assume β =1 and consider X to be Weibull distributed with CDF and PDF as defined
in the previous section. The second CDF in Definition 4.4 implies the following
Theorem 5.4. The CDF of the Ampadu APT-{Quantile Exponential-Weibull} distribution
of type II is given by
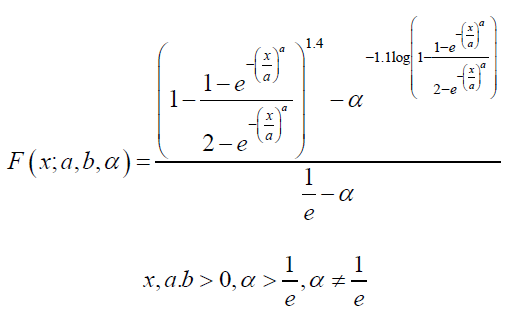
Remark 5.5. If a random variable L has CDF given by the theorem immediately above, we write
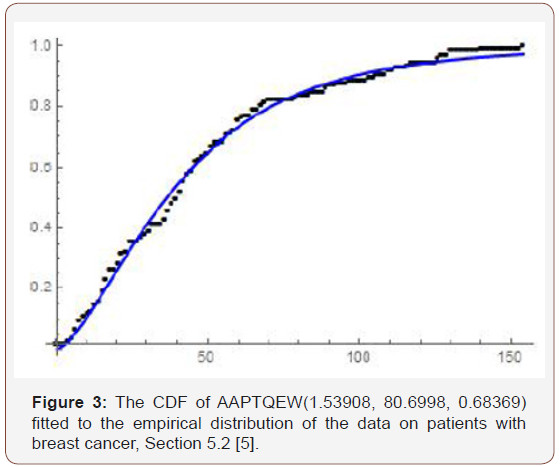
L ~ AAPTQEW(a,b,α) (Figure 3)
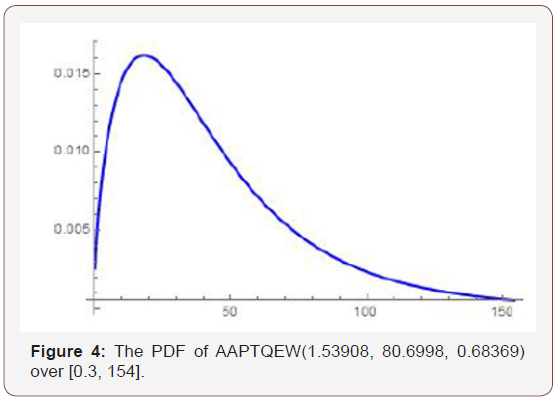
Remark 5.6. By differentiating the CDF of the AAPTQEW distribution, the PDF can be obtained (Figure 4).
Application of Definition 1.6
We assume β =1, α =1.3 , X is Weibull distributed with CDF and PDF as defined in Section 5.1, and T is a fully specified Cauchy distribution. In particular, we assume T has CDF
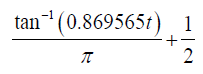
so that the quantile of T is given by
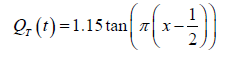
The second CDF in Definition 3.6 implies the following
Theorem 5.7. The CDF of the Ampadu APT-{Quantile Cauchy- Weibull} distribution of type III is given by
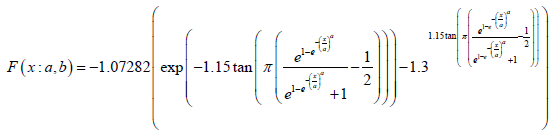
where x, a, b > 0
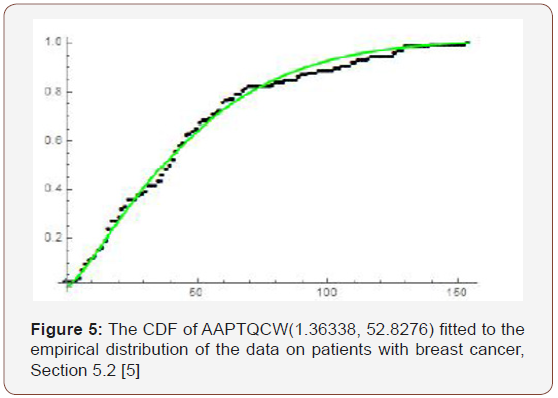
Remark 5.8. If a random variable V has CDF given by the theorem immediately above,
we write V ~ AAPTQCW(a,b) (Figure 5)
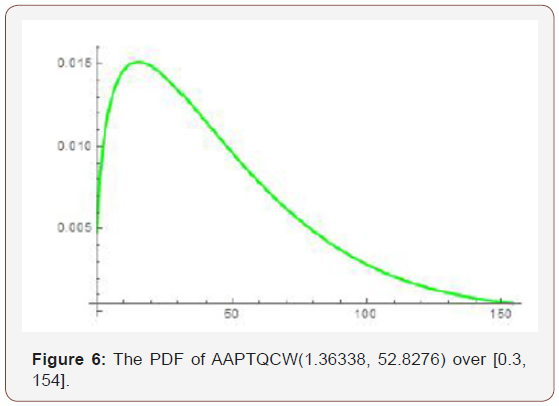
Remark 5.9. By differentiating the CDF of the AAPTQCW distribution, the PDF can be obtained (Figure 6)
Further Developments and Concluding Remarks
Inspired by the APT-G distribution in [1], we ask the reader to
investigate properties and applications of a so-called 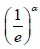 power
transform distribution
power
transform distribution 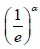 PT-G for short)
PT-G for short)
Definition 6.1. A random variable Z will be called 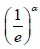 PT-G
distributed if the CDF is given by
PT-G
distributed if the CDF is given by
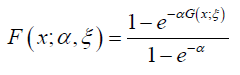
For 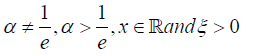
Remark 6.2. The PDF can be obtained by differentiating the CDF
The new distribution appears practically significant in modeling real-life data as shown below. We assume G is given by the CDF of the Weibull distribution, as in Section 5.1. Thus, from the above definition the following is immediate
Theorem 6.3. The CDF of the 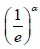 PT-Weibull distribution is
given by
PT-Weibull distribution is
given by
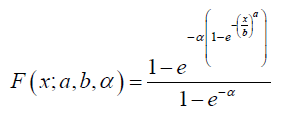
For 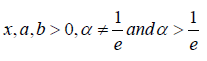
Remark 6.4. If a random variable M has CDF given by the theorem immediately above,
we write  (Figure 7)
(Figure 7)
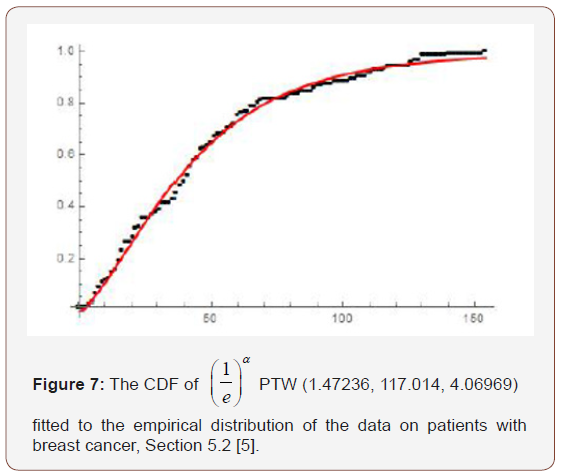
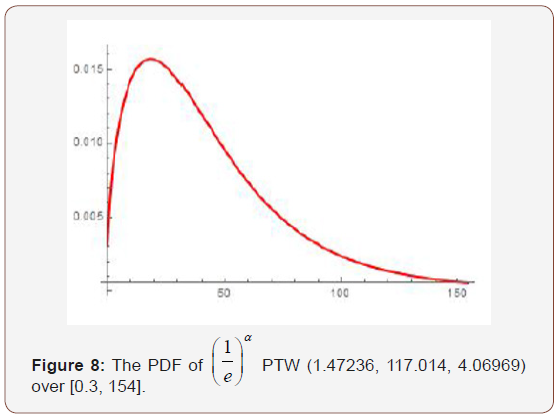
Remark 6.5. By differentiating the CDF of the 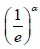 PTW distribution, the PDF can be obtained (Figure 8).
PTW distribution, the PDF can be obtained (Figure 8).
Whilst we have shown the distributions are practically significant in the health sciences, we hope they find applications in other disciplines. Also we hope the researchers will further develop the mathematical and statistical properties of these distributions.
Acknowledgement
None.
Conflict of interest
No conflict of interest.
References
- Mahdavi A, Kundu D (2017) A new method for generating distributions with an application to exponential distribution. Communications in Statistics-Theory and Methods 46(13): 6543-6557.
- Zubair Ahmad, Muhammad Ilyas, GG Hamedani (2016) The Extended Alpha Power Transformed Family of Distributions: Properties and Applications. Journal of Data Science.
- Clement Ampadu, Results in Distribution Theory and Its Applications Inspired by Quantile Generated Probability Distributions, Lulu.com. ISBN: 0359249957,9780359249954.
- Clement Boateng Ampadu (2018) Quantile-Generated Family of Distributions: A New Method for Generating Continuous Distributions. Fundamental Journal of Mathematics and Mathematical Sciences, Volume 9(1): 13-34.
- Girish Babu Moolath, Jayakumar K(2017) T-Transmuted X Family of Distributions. STATISTICA 3.
-
Clement Boateng Ampadu. The Ampadu APT − qT − X Family of Distributions Induced by V with an Illustration to Data in the Health Sciences. Annal Biostat & Biomed Appli. 2(1): 2019. ABBA.MS.ID.000526.
Public Health, Health Science, Mathematics, Data Science, Statistics-Theory, Family of Distributions, Mathematical Sciences, Statistical properties, Breast cancer, Patients Data
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






