 Research Article
Research Article
Optimal Designs for M-Allel Crosses in One and Two-Way Setting
MK Sharma, Addis Ababa University, Addis Ababa, Ethiopia.
Received Date: September 27, 2018; Published Date: December 14, 2018
Abstract
Recently authors [1] constructed optimal Block and Row-Column designs for complete diallel cross (CDC) methods by using nested balanced incomplete block designs.In this article we are presenting methodof constructionof three series of optimal block and row-column designs for partial double cross by usingthese designs. Ourproposed optimal block and row-column designs for partial double cross are new and not available in statistical literature.AMS classification: 62k 05
Keywords: Nested balanced incomplete block design; Complete diallel cross;Partal double cross; Row and Column design; Block design
Introduction
Mating design involving multi–allele cross m (≥2) lines play very important role to study the genetic properties of a set of inbred lines in plant breeding experiments. A most common mating design in genetics is the diallel cross which consist ofv=p(p-1)/2 crosses of p inbred lines such that the crosses of the type (i × j) = (j × i) for i,j = 1,2, …, p.This type of mating design is called complete diallel cross (CDC) method 4 of Griffing[2]. The concept of CDC can be easily extended to double cross designs. A double cross design is obtained by crossing two unrelated F1 hybrids symbolized as (i ×j) and (k × l), where i ≠j≠k ≠l ≠i, are 4 parents and (i× j) and (k × l) are two F1’s[3].
Let nc denote the total number of crosses (experimental units) involved in an m-allele cross experiment, where m=2 or 4. Generally double cross experiments are conducted using a completely randomized design (CRD) or a randomized complete block (RCB) design involving some or all nc crosses as treatments. The number of crosses in such a mating design increases rapidly with increase in the number of lines. It leads to an overall inefficient experiment. It is for this reason that the use of incomplete block design as environment design is needed for double cross experiments [3].
Parsad et al. [4] constructed optimal block designs for double cross experiments by using balanced incomplete block designs and nested balanced incomplete block designs of Morgan et al. [5]. Sharma & Tadesse [6] constructed double cross designs for even and odd value of p by using initial block of unreduced balanced incomplete block designsgiven by Bose et al. [7] and initial block of row –column designs given byGupta & Choi [8], respectively.
In this paper we have used nested balanced incomplete block designs of Dey et al. [9] and Morgan et al. [5] for the construction of three seriesof optimal block and row-column designs for partial double cross experiment. The parameters of ourproposed optimal block and row-column designs for partial double cross experiments are different from Parsad et al. [4] designs. We have used those designs of Morgan et al [5] for the construction of partial double cross experiment which Parsadet al. [4] did not use.In our proposed designs every cross is replicated equal number of times in a design. We have considered the model that includes the gca effects, apart from block effects, but no specific combining ability effects.
Some definitions
a. Definition 2.1: The double cross has been defined by Rawlings
and Cockerham (1962 b) as a cross between two unrelated F1
hybrids, say denoted by (i ×j) and (k× l), wherei ≠j ≠k ≠ l ≠i,
are denoting the grandparents and no two of them are same.
Ignoring reciprocal crosses, with p grandparents, there will be 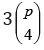 double crosses.
double crosses.
b. Definition 2.2:An arrangement ofv treatments each replicatedr* times in two systems of blocks is said to be a nested balanced incomplete design (NBIBD) with parameters (v, b1, k1, r*, λ1, b2, k2, λ2, m) if
• The second system is nested within the first, with each block from the first system, containing exactly m blocks from the second system (sub blocks);
• ignoring the second system leaves a balanced incomplete block design with parameters v, b1, k1, r*, λ1;
• ignoring the first system leaves a balanced incomplete block design with parametersv, b2, k2, r*, λ2.
The following parametric relations hold for a nested balanced incomplete block design:
(i) v r*= b1 k1=m b1 k2=b2 k2
(ii) (v-1) λ1= (k1 -1) r*
(iii) (v-1) λ2= (k2 -1) r*
Universal optimality of designs for 1-way- heterogeneity
Following Parsad et al. [4], let dbe a block design for an m-allel cross experiment involving p inbred lines, b blocks each of size k. This means that there are k crosses in each of the blocks of d. Further,let rdt and sdi denote the number of replication of the tth cross and the number of replications of the ith line in different crosses,respectively, in d [t = 1,2, …, nc; i = 1,2,…,p] . Evidently, Σrt= bk, Σsi= mbk = mn and n = bk, the total number of observations. We also considered this and we took the following additive model for the observations obtained from design d.
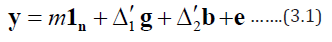
where yis an n×1 vector of observations, 1is an n×1 vector
of ones, 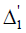 is an n × p design matrix for lines
is an n × p design matrix for lines 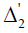 and is an n × b
design matrix for blocks, that is, the (h,l)th element of
and is an n × b
design matrix for blocks, that is, the (h,l)th element of 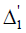 ( also of
( also of 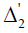 ) is 1 if thehth observation pertains to the lth line (also of block) and is zero otherwise. μ is a general mean, g is a p × 1 vector of line
parameters, β is a b × 1 vector of block parameters and e is an n
× 1 vector of residuals. It is assumed that vector βis fixed and e is
normally distributed with mean 0andVar (e) = σ2 IwithCov (β, e)= 0,
where Iis the identity matrix of conformable order.
) is 1 if thehth observation pertains to the lth line (also of block) and is zero otherwise. μ is a general mean, g is a p × 1 vector of line
parameters, β is a b × 1 vector of block parameters and e is an n
× 1 vector of residuals. It is assumed that vector βis fixed and e is
normally distributed with mean 0andVar (e) = σ2 IwithCov (β, e)= 0,
where Iis the identity matrix of conformable order.
For the analysis of proposed design d, the method of least squares leads to the following reduced normal equations for estimating the linear functions of the gca effects of lines under model (3.1).
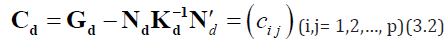
where Gd = 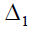
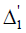 = (gdii´), gdii = sdi and for i≠i´ ,gdii´ is the number
of crosses in d in which the linesi and i´ appear together . Nd =
= (gdii´), gdii = sdi and for i≠i´ ,gdii´ is the number
of crosses in d in which the linesi and i´ appear together . Nd = 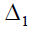
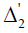 = (ndij), ndij is the number of times the line i occurs in block jof dand
= (ndij), ndij is the number of times the line i occurs in block jof dand
Kd = 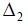
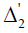 is the diagonal matrix of block sizes.
is the diagonal matrix of block sizes.
A design d will be called connected if and only if rank (Cd) = p -1, or equivalently, if and only if all elementary comparison among gca effects are estimable using d. We denote byD(p,b,k), the class of all such connected block design {d} with p lines, b blocks each of size k. To prove optimality of design d,we need the following well known lemma [10].
Lemma 3.1 For given positive integers s and t, the minimum
of  where ni’s are non-negative integers, is
obtained when t – s [t/s] of the ni’s are equal to [t/s]+1 and s - t +
s[t/s], where [z] denotes the largest integer not exceeding z. The
corresponding minimum of
where ni’s are non-negative integers, is
obtained when t – s [t/s] of the ni’s are equal to [t/s]+1 and s - t +
s[t/s], where [z] denotes the largest integer not exceeding z. The
corresponding minimum of
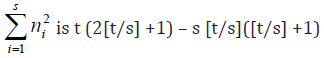
Theorem 3.1:For any design d ε D (p, b, k)
tr (Cd)≤k-1b{m k (k -1-2x) + px (x+1)}
where x= [mk/p] and for a square matrix A, tr (A) stands for the sum of the diagonal elements of A.
Proof.For any design d ε D (p, b, k), we have
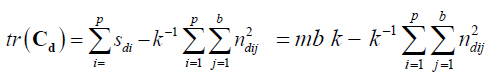
Now, since 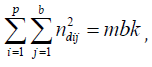 using Lemma 3.1
using Lemma 3.1
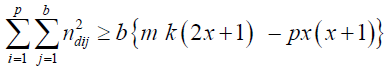 where [mk/p].
where [mk/p].
Hence
tr(Cd) ≤ mbk– k-1b{m k(2x +1) – p x (x+1)} = k -1b {m k (k-1 -2 x) + p x (x+1)}
By Lemma 3.1, the above equality is attained if and only if ndij= x or x+1, for i =1,2, . . ., p; j = 1, 2, . . ., b
Theorem 3.1:For any design d ε D (p, b, k)
tr (Cd)≤ k-1b{ mk (k -1-2x) + p x (x+1)
where x = [mk/p] and for a square matrix A, tr (A) stands for the sum of the diagonal elements of A.
Kiefer [11] showed that a design is universally optimal in a relevant class of competing design if (i) the information matrix ( the Cd– matrix) of the design is completely symmetric in the sense that Cd has all its diagonal elements equal and all of its offdiagonal elements equal, and (ii) the matrix Cd has maximum trace in the class of competing designs, that is, such a design minimize the average variance of the best linear unbiased estimators of all elementary contrasts among the parameters of interest i.e. the general combining ability in our context. On the basis of the theorem 3.1 and Kiefer criterion of the universal optimality, we can state Theorem 3.2.
Theorem 3.2:For any design d* ε D (p, b, k) be a block design for m-allel crosses satisfying
(i) tr (Cd*)=k-1 b{ mk (k -1-2x) + p x (x+1)
(ii) Cd* = (p-1)-1k-1 b {m k (k -1-2x) + p x (x+1)} (Ip –1p 1′p/ p)
is completely symmetric.
where Ip is an identity matrix of order p and 1p1′p is a p × p matrix of all ones. Furthermore, using d* all elementary contrasts among gcaeffects are estimated with variance
[2b-1(p-1)k/ {m k (k-1-2x) + p x(x+1)}] σ2.
Then d* is universally optimal in D (p, b, k), and in particular minimizes the average variance of the best linear unbiased estimator of all elementary contrasts among the general combining ability effects.
Universal optimality of designs for 2-way- heterogeneity
Consider an m-allel cross involving p lines in a row-column design with k rows and b columns. The model can be written as given below
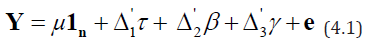
where Yis an n × 1 vector of observed responses, μ is the general
mean, τ ,β and γ are the column vectors of pgcaparameters, krow
effects and b column effects, respectively, 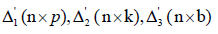 are the corresponding design matrices, respectively and e denotes
the vector of independent random errors having mean 0 and
covariance matrix σ2 In.
are the corresponding design matrices, respectively and e denotes
the vector of independent random errors having mean 0 and
covariance matrix σ2 In.
Let 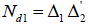 be ap × k incidence matrix of lines versus rows and
be ap × k incidence matrix of lines versus rows and 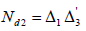 be a p × b incidence matrix of treatments versus columns and
be a p × b incidence matrix of treatments versus columns and 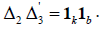 Let rdld enote the number of times the lth cross appears in the design d,l = 1, 2,…,v and similarlysdi denote the
number of times the ith lineoccurs in thedesign d, i = 0, 1, . . . p-1.
Under (4.1), it can be shown that the reduced normal equations for
estimating the treatment effects, after eliminating the effect of rows
and columns, are
Let rdld enote the number of times the lth cross appears in the design d,l = 1, 2,…,v and similarlysdi denote the
number of times the ith lineoccurs in thedesign d, i = 0, 1, . . . p-1.
Under (4.1), it can be shown that the reduced normal equations for
estimating the treatment effects, after eliminating the effect of rows
and columns, are
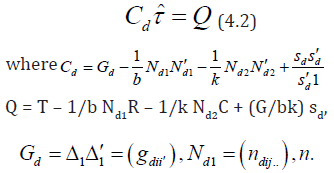
is the number of times the line i occurs in row jof d, 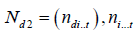 is the number of times cross ioccurs in column
t.Q is a p × 1 vector of adjusted treatments (crosses) total, T is a
p × 1 vector of treatments (lines) totals, R is a k × 1 vector of rows
totals, Cis a b ×1 vector of columns totals, and G is a grand total of
all observations.
is the number of times cross ioccurs in column
t.Q is a p × 1 vector of adjusted treatments (crosses) total, T is a
p × 1 vector of treatments (lines) totals, R is a k × 1 vector of rows
totals, Cis a b ×1 vector of columns totals, and G is a grand total of
all observations.
We use the following theorems ofPrasadet al. [4] to prove optimality of the proposed designs.
Theorem 4.1: For any design d Ɛ D1(p, b, k), trace (Cd)will be maximum when
(i) 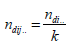 ie., the design is orthogonal with respect to the lines
vs rows as blocks classification or a row –regular setting with
respect to lines.
ie., the design is orthogonal with respect to the lines
vs rows as blocks classification or a row –regular setting with
respect to lines.
(ii) 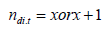 where
where 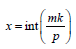 ie., the lines appear either x or
x=1 time in columns as blocks classification, where m = 2 or 4.
ie., the lines appear either x or
x=1 time in columns as blocks classification, where m = 2 or 4.
Theorem 4.2:Let d* Ɛ D1(p, b, k) be a row – column design satisfying
a. trace (Cd*) =k-1b{m k(k-1-2x) + p x (x+1)
b. Cd* is completely symmetric.
Then d* is universally optimal in D1 (p, b, k)
Now we will show a connection between optimal block and rowcolumn design for optimal partial double cross design with nested balanced incomplete block designs of Preece (1967).Consider now a NBIB design d obtained by developing mod (v) t1 initial blocks, each sub-divided into t2 sub-blocks. The parameters of such an NBB design are v= p, b1= vt1, b2= b1 t2 , k1= 2t2, r*, k2 =2. If we identify the treatments of d as lines of a diallel experiment and perform double crosses among the lines appearing in the same sub block of dand arrange these sub-blocks into one bigger block and develop mod (v), we get a design d* for a double cross experiment involving p lines with b2crosses arranged in b = b1/2 blocks.Each double cross is replicated once. Such a design d* belongs toD (p, b, k). For such a design nd*ij = 0 or 1for i = 1, 2, . . . ,p, j = 1, 2, . . . , b. and
Cd*= (p-1)-1[ (p-1) (p-5)Ip –(3p-7)1p1’p](4.3)
Clearly Cd* given by (4.3) is completely symmetric and tr (Cd*) = p (p-5) which equals the equality given in theorem 4.2:Thus the design d* is optimal in D1 (p, b, k) and using d* each elementary contrast among gca effects is estimated with a variance
2 σ2/ p (p-5)(4.4)
If p is even then the NBIB design has the following parameters.
v= p, b1= (v-1) t1, b2= rb1 k2 , k1= 2r k2, r*, k2=2., where r is the numberof replication of double cross. If we perform the same procedure given above, we get a design d* for a partial double cross experiment involving p lines with b2 crosses arranged in b = b1/ t1 blocks. Such a design d*εD (p, b, k); also, for such a design nd*ij= 1 or 2for i = 1, 2, . . . ,p, j = 1, 2, . . . , b. and
Cd* = (r t1)-1[r2 (p-1) (t1-1)Ip – r2 (p- t1-1)1p1’p](4.5)
Clearly Cd* given by (4.5) is completely symmetric and tr (Cd*) = p (p-5) which equals the equality given in theorem 3.2. Thus, the design d* is optimal in D (p, b, k) and using d* each elementary contrast among gca effects is estimated with a variance
2 σ2 r(p-1) (t1-1)/ t1(4.6)
Hence, we state the following theorems.
Theorem 4.3:The existence of a nested balanced incomplete block design d with parameters
v= p, b1= vt1, b2= b1t2, k1= 2t2, r*, k2=2 ,where p is odd, implies the existence of optimal block and row-column designs for partial double cross.
Theorem 4.4:The existence of a nested balanced incomplete block design d with parameters
v= p, b1= (v-1) t1, b2= rb1 k2, k2= 2r k2, r*, k2=2,wherep iseven, implies the existence of optimal block design for partial double cross.
Method of Construction
Series 1: Let p = 4m+1, m ≥ 1 be a prime or a prime power and x be a primitive element of the GF (p). Consider the following m initial blocks.
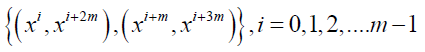
As shown by Dey et al. [9], these initial blocks, when developed in the sense of Bose [7], give rise to a nested balanced incomplete block design with parameters v = p = 4m +1,
k1 = 4, b1= m (4m+1), k2 =2. Arrange the following m initial blocks into single block
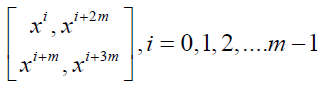
By making pair of crosses in a single block and developing mod (p), we get double cross design with parameters p = 4m+1, b = 4m+1, k = k1/2.
Note1: For construction of double cross design it is necessary that the block size of a single block must be an even number i.e. m must be a multiple of 2.
The procedure to obtain the above designs has been explained by the following illustrative example.
Example 1:If we let m = 2, we get the following two blocks.
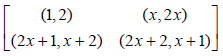
We can now write both blocks in a single block as given below.
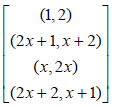
where xis a primitive element of GF(32).Now cross the elements of the individual block and put these crosses in a single block. Adding successively the non-zero elements of GF (32) to the contents of the single block, we obtain block and row- column design for partialdouble cross experiment with parameters p= 9, b= 9, k= 2.The design is exhibited below, where the lines have been relabelled 1-9, using the correspondence 0→1, 1→2, 2→3, x→4, x+1→5, x+2→6, 2x→7, 2x+1→8, 2x+2→9:
➣ Partial Double Cross Row-Column Design
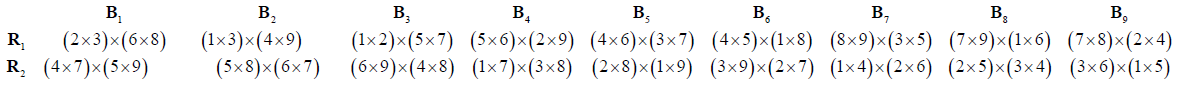
Series 2: Let p = 6m+1, m ≥ 1 be a prime or a prime power and x be a primitive element of the Galois field of order p. Consider the initial blocks
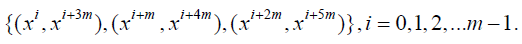
Dey et al. (1986)[4]showed when these initial blocks developed over mod (p), give a solution of a nested incomplete block design with parameters v = p = 6m+1, b1 = m(6m+1), k1 =6, k2 = 2, λ2= 1.
We can then arrange the above initial blocks into a single block as given below
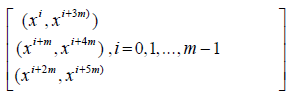
Example 2: Let m = 2. Then we get the following two initial blocks.
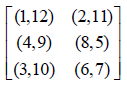
We can arrange these two blocks in a single block as given below.

Now performing crosses in pairs and developing these crosses over mod(p), we obtain block and row-column design with parameters p =13, b = 13 and k =3

➣ Partial Double Cross Row-Column Design
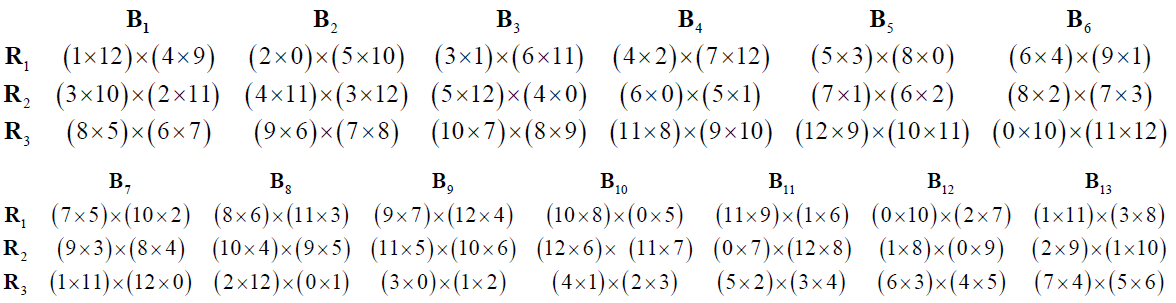
Series 3: Let p = 2m +1, m≥ 2 be a prime or a prime power and considerthe following m blocks
(0, 2m), (1, 2m-1), (2, 2m-2), . . ., (m-1, m+1) mod (2m+1)
Example 3:If we let m= 4, then the single block will be as given below.

Now applying the procedure given in example 1, we can obtain an optimal block design for double cross experiment with parameters p = 9,k= 2, b = 9.
Note 2:The m blocks given in series 3 form a nested balanced incomplete block design with parameters v = p = 2m +1, b1 = m, k1= m(2m+1), k2 = 2, λ2= 1 given by Dey et al.[9].
Example: 4Consider MRP 33 (2001) design with initial blocks given by
[{(∞ 0) (5 10)}{(1 2) (4 8)}{(6 9) (7 13)}{11 3) (12 14)}] mod 15.
Arranging these initial blocks in a single block and performing crosses between sub- blocks anddeveloping mod(15), treatment ∞ is invariant under cyclic development of the initial blocks and we get optimal partial double crossblock design with parameters p = 16, b =15, and k =4.
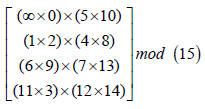
Discussion
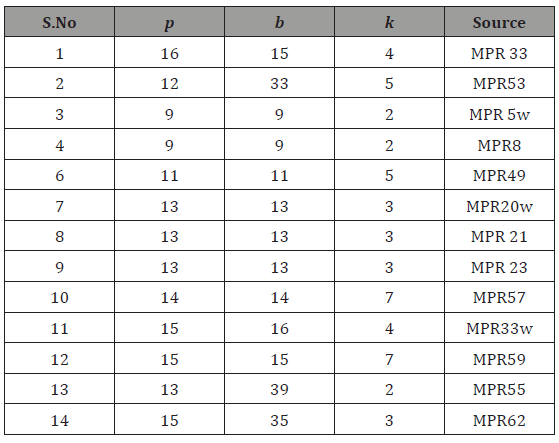
Universally optimal partial double cross design with p≤16, s ≤30 obtained by the above method from NBIB designs of Morgan, Preece& Rees [5], are listedin the following Table 1. These are the designs other than the designs catalogued by Das, Dey & Dean [12] and Parsad, et al.[4]. These are the new designs and successfully can be used in agricultural experimentation.
Table 1: Universally optimal block design for double cross with p ≤ 16, s ≤ 30 generated by using NBIB designs of Morgan et al. [5].
Conclusion
We have presented a method of construction of three series of optimal block and row-column designs for partial double cross by using nested balanced incomplete block designs. Our proposed optimal block and row-column designs for partial double cross are new and not available in statistical literature.
Acknowledgement
None
Conflict of Interest
No conflict of interest.
References
- Sharma MK, Tadesse M (2016) Optimal block designs for double cross experiments. Communication and Statistics 45(15): 4392-4396.
- Griffings B (1956) Concepts of general and specific combining ability in relation to diallel crossing system. Aust J Bio Sci 9: 463-493.
- Singh M, Gupta S, Parsad R (2012) Genetic crosses experiments. In: Design and Analysis of Experiments-Vol. Wiley: New York, USA: 1-71.
- Parsad R, Gupta VK, Gupta S (2005) Optimal Designs for Diallel and Double Cross Experiments. Utilitas Mathematica 68: 11.
- Morgan JP, Preece DA, Rees DH (2001) Nested balanced incomplete block designs. Discrete Mathematics 231: 351-389.
- Sharma MK, Tadesse M (2016) Optimal block and row-column designs for CDC methods. Sankhya Ser B: 1-14.
- Bose RC (1939) On the construction of balanced incomplete block designs. Ann Eugen 9: 353- 399.
- Gupta S, Choi KC (1998) Optimal row-column designs for complete diallel crosses, Communication in Statistics-Theory and Methods 27(11): 2827-2835.
- Dey A, Das US, Banerjee AK (1986) Construction of nested balanced incomplete block designs. Calcutta Statist. Assoc Bull 35: 161-167.
- Cheng CS (1978) Optimality of certain asymmetrical experimental designs. Ann Statist 6(6): 1239-1261.
- Kiefer J (1975) Construction and optimality of generalized Youden designs. In: Srivastava JN (ed), A Survey of Statistical Desigmn and Linear Models. North- Holland Amesterdam, Netherlands, pp. 333-353.
- Das A, Dey A, Dean MA (1998) Optimal designs foe diallel cross experiments. Statistics & Probability Letters 36(4): 427-436.
-
MK Sharma, Mekonnen Tadesse. Optimal Designs for M-Allel Crosses in One and Two-Way Setting. Annal Biostat & Biomed Appli. 1(2): 2018. ABBA.MS.ID.000509.
Computer Science, Econometrics, Financial Mathematics, Environ Metrics, Image Analysis, Image Processing, Behaviometrics, Big Data Analytics, Binary and Non-normal Continuous Data, Binomial Regression, Biometrics, Soft Biometrics
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






