 Review Article
Review Article
Maximum Likelihood Estimation in the Ampadu-G Family of Distributions
Clement Boateng Ampadu, Department of Biostatistics, USA.
Received Date: March 29, 2019; Published Date: April 26, 2019
Abstract
In this paper the maximum likelihood estimation for parameters in the Ampadu-G family of distributions [1] is discussed. When G is given by the normal distribution, we assess the performance of the estimation procedure via simulation study carried out in the software package R [2]. As a further development we conjecture the methods of maximum product spacings and least squares are adequate for estimating the parameters in the Ampadu-G family of distributions.
Keywords: Ampadu-G; Normal distribution; Maximum likelihood estimation; Ordinary least squares estimation; Maximum product spacings estimation; Monte carlo simulation
Introduction and Preliminaries
At first, we recall the following
Definition 3.1: [1] Letλ > 0,ξ > 0 be a parameter vector all of
whose entries are positive, and x ∈
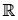 . A random variable X will be
said to follow the Ampadu-G family of distributions if the CDF is
given by
. A random variable X will be
said to follow the Ampadu-G family of distributions if the CDF is
given by
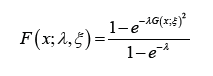
and the PDF is given by
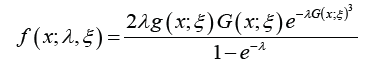
where the baseline distribution has CDF G( x;ξ )and PDF g ( x;ξ )
The Quantile
Theorem 4.1. Let QG (•) = G−1 (•) denote the quantile of some base distribution with CDF G and PDF g,λ > 0, and 0 < u <1. The quantile function of the Ampadu-G family of distributions is given by
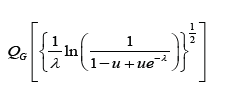
Proof. Let 0 < u <1. Since QG (•) = G−1 (•) the quantile function can be obtained by solving the following equation for y
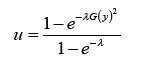
Random Number Generation
If u U (0,1) , that is, u is a uniform random variable, then a random sample from the Ampadu-G family of distributions can be obtained via
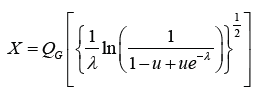
Where QG (•) = G−1 (•) denote the quantile of some base distribution with CDF G and PDF g, and λ > 0
Parameter Estimation
In this section, we obtain the maximum likelihood estimators (MLEs) for the parameters of the Ampadu-G family of distributions. For this, let X1,X2, · · · ,Xn be a random sample of size n from the Ampadu-G family of distributions. The likelihood function is given by
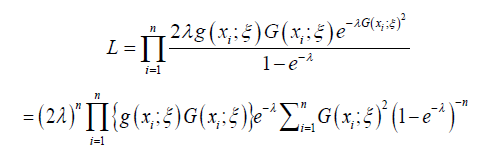
From the above the log-likelihood function is given by
→ So we will have the final result:
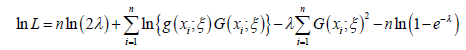
The MLE’s of ξ and λ can be obtained by maximizing the equation immediately above. The derivatives of the equation immediately above with respect to the unknown parameters are given as follows
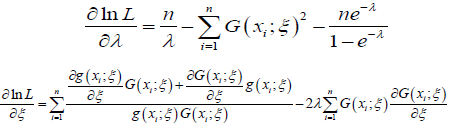
Now solving the system below forξ and λ gives the maximum
likelihood estimators, 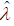 and
and 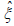 of the unknown parameters:
of the unknown parameters:
So we have the following new model (ρ ,m,v) :
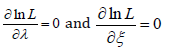
Simulation Study
In this section, a Monte Carlo simulation study is carried out to assess the performance of the estimation method, when G is given by the normal distribution. First, we present the CDF and PDF of the Ampadu-Normal distribution.
Theorem 7.1. The CDF of the Ampadu-Normal family of distributions is given by
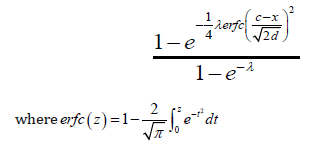
By differentiating the CDF in the previous theorem, we get the following
Theorem 7.2. The PDF of the Ampadu-Norma family of distribution is given by
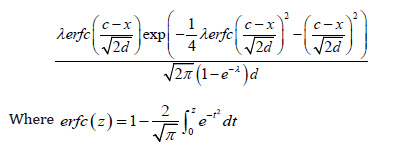
Remark 7.3. If a random variable W follows the Ampadu-Normal family of distributions, we write W ~ AN (λ,c, d ) (Figure 1 &2).
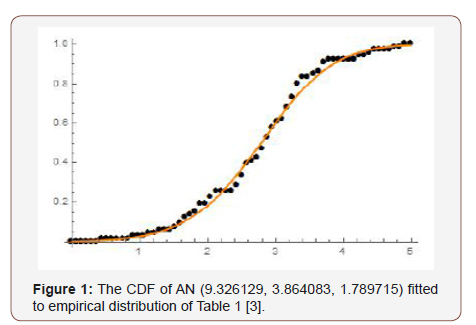
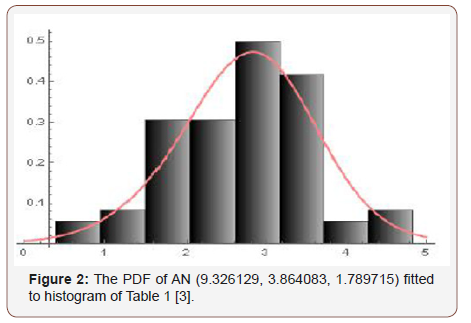
Samples of sizes 200, 350, 500, and 700, are drawn from the Ampadu-Normal family of distributions. The samples have been drawn for (λ,c,d ) = (9.3, 3.8, 1.7) , and the maximum likelihood estimators for the parameters λ , c, and d are obtained. The procedure has been repeated 200 times and the mean and mean square error for the estimates are computed, and the results are summarized in Table 1 below.
Table 1: Result of Simulation Study.
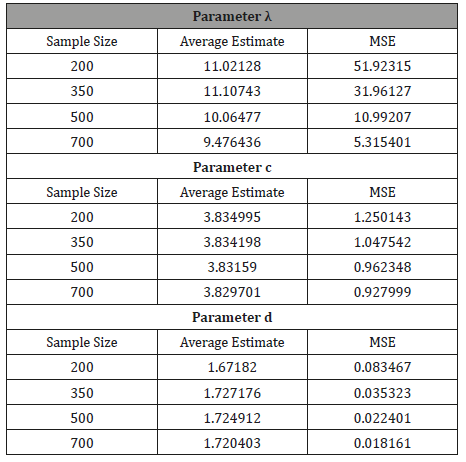
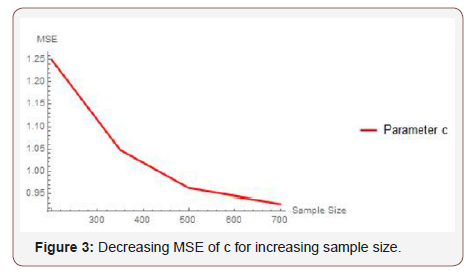
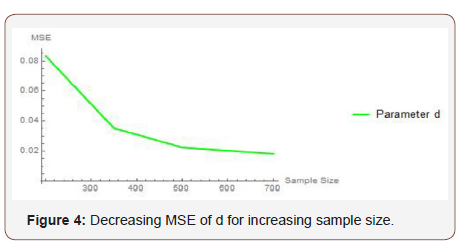
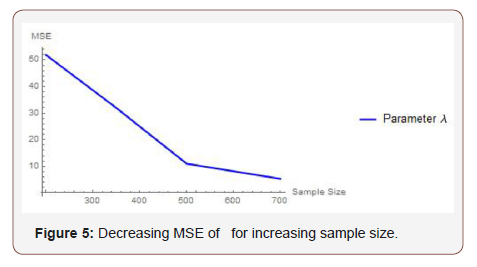
From Table 1 above, we find that the simulated estimates are close to the true values of the parameters and hence the estimation method is adequate. We have also observed that the estimated mean square errors (MSEs) consistently decrease with increasing sample size as seen in the Figures below (Figure 3,4,5).
Concluding Remarks and Further Developments
In this paper we have shown that estimating the parameters in the Ampadu-Normal family of distributions by the method of maximum likelihood is adequate via a brief simulation study. As a further development we propose the following
Exercise 8.1. Conduct a simulation study to determine if the methods of maximum product spacings, and ordinary least squares are adequate in estimating the parameters in the Ampadu-Normal family of distributions.
Remark 8.2. The methods of maximum product spacings and ordinary least squares are discussed in [4].
Acknowledgement
None.
Ethics
No conflict of interest.
References
- Clement Boateng Ampadu (2019) The Ampadu-G Family of Distributions with Application to the T-X(W) Class of Distributions. Annal Biostat and Biomed Appli 1(4).
- R version 3.5.2 (2018). Copyright (C) 2018 The R Foundation for Statistical Computing.
- Ayman Alzaatreh, Carl Lee and Felix Famoye (2014) T-normal family of distributions: a new approach to generalize the normal distribution. Journal of Statistical Distributions and Applications 1:16
- Zubair Ahmad (2018) The Zubair-G Family of Distributions: Properties and Applications. Annals of Data Science.
-
Clement Boateng Ampadu. Maximum Likelihood Estimation in the Ampadu-G Family of Distributions. Annal Biostat & Biomed Appli. 2(1): 2019. ABBA.MS.ID.000530.
Ampadu-G; Normal distribution; Maximum likelihood estimation; Ordinary least squares estimation; Maximum product spacings estimation; Monte carlo simulation
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






