 Research Article
Research Article
Robust Stabilization of a Class of Non-Triangular Nonlinear Systems
Guangping He*, Junjie Yuan, Mengying Zhang, Lei Zhao and Quanliang Zhao
Department of Mechanical and Electrical Engineering, North China University of Technology, P.R. China
Corresponding AuthorGuangping He, Department of Mechanical and Electrical Engineering, North China University of Technology, P.R. China.
Received Date:June 02, 2023; Published Date:July 31, 2023
Abstract
Globally asymptotical stabilization (GAS) of a class of nonlinear systems is investigated in the present paper. As the inherent robust stability of the non-smooth feedbacks for the external disturbances and the un-modeled errors, the Hölder continuous but non-smooth feedbacks is investigated to stabilize a class of nonlinear systems with non-triangular forms. A new finite-time stabilizing controller is presented for the single-input sing-output (SISO) non-triangular nonlinear systems with considering some additional conditions. Some numerical simulations are included to demonstrate the stability of the presented control scheme.
Keywords:Robust stabilization; Non-triangular systems; Nonlinear Systems; Finite-Time stabilization; control
Introduction
For the nonlinear systems with triangular normal form, such as the (strict) feedback forms

have been extensively investigated during the past twenty years. Now it is well known that the former can be globally asymptotically stabilized by backstepping-based control methods [1], while the later can be globally asymptotically stabilized by the nested saturation feedbacks [2,3] or the forwarding procedures [2,4]. In this paper, the GAS of a class of highly nonlinear systems with nontriangular forms is investigated. Due to the important applications in underactuated mechanical systems [5], the nonlinear dynamic systems under consideration can be generally expressed as
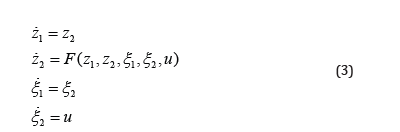
It is intuitionally, if the nonlinear term of the right-hand side of (3) satisfies
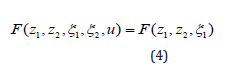
then the non-triangular nonlinear systems (3) degenerate to the strict feedback forms. When the nonlinear function (z1,z2,ξ1,ξ2,u)has a form
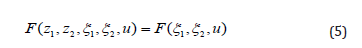
then the systems (3) is simplified to the feedforward systems. The primary limitation of stabilization of nonlinear systems in non-triangular forms (3) is because of the “peaking phenomenon” that was pointed out by Sussmann and Kokotović [6]. The problem is that driving the subsystem ξ1,ξ2 exponentially fast to zero using a linear partial state feedback does not necessarily asymptotically stabilize the composite system in (3). Such a partial state feedback might cause the subsystem (z1,z2) to have finite escape time. To overcome the effect of peaking in the stabilization of the non-triangular systems (3), the researches followed in this direction commonly restrict the form of the nonlinear terms either by structural requirements [1,7] or by growth conditions [2, 6, 8] to prevent the possibility of finite escape time. The structure restrictions lead to the researches of nonlinear systems with triangular forms, while the growth conditions lead to the applications of saturated feedback with small gains. The main drawback of all existing bounded controller with small gain feedback is the relatively poor performances, such as the large settling time, the possibility of slow peaking [8], and the low resistibility on the external disturbance [2].
It is different from the research directions for finding the globally asymptotical controllers on the basis of the relatively accurate nonlinear dynamics model. The robust controls, such as the high-order sliding mode [9], H∞ controllers [10], and fractionalpower- based feedbacks [11], etc. also provide the important research directions for controlling the highly nonlinear systems. The H∞-based control for the nonlinear systems is intractable in solving the Hamilton-Jacobi-Isaacs (HJI) equations. The high-order sliding mode control is difficulty in proving the stability of the controller because of using the discontinuous feedbacks. To date, these two kinds of robust control design methods are primarily limited to some special homogeneous nonlinear systems or even the linear systems. The fractional-power feedback is a kind of Hölder continuous [11] but non-smooth feedback techniques. By the “adding a power integrator” method [12], the Lyapunov function can be constructed systematically, and the robust control method is not limited to the triangular systems. Inspired by the works of [13- 16], in this paper the GAS of the non-triangular nonlinear system (3) with some additional conditions is investigated by applying the fractional-power feedback.
This paper is organized as follows. In section 2, the essence the control problem for the nonlinear system (3) is analyzed. A robust finite-time stabilizing controller is presented in the section 3. In section 4, a specific example is employed to numerically demonstrate the stability of the presented controller. The conclusions and some discussions are provided in the last section.
The inherent characteristics of the control problem of the nonlinear system (3)
According to the Lyapunov stabilization theory, the essence of the control problem of the nonlinear system (3) is to find an input u and a positive-definite and proper function V =V(z1,z2,ξ1,ξ2,t)>0 , such that lim→∞ = 0 is satisfied, where t be the time variable. Due to the special structure of system (3), the control problem of it can be changed to design a function Fz(z1,z2,t), such that the differential equation.
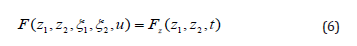
has unique solution u(t) and it drives the system (3) satisfies lim t→∞V = 0 . We will show in the sequel that solving the nonlinear differential equation (6) can be simplified to solve an algebraic equation with considering some additional conditions. Before showing that, the following theorem is necessary to be introduced.
Theorem 1: For the nonlinear system (3), assume the function F(z1,z2,ξ1,ξ2,u) is independent of the input u , and the following set of the ordinary differential equations.


then the controller (9) renders the origin of the non-triangular nonlinear system (12) GAS. This completes the proof.
Remark 1: The obstacle of using the theorem 1 is that the differential equations (7) are intractable generally. For a general case, one has to use a numerical method to solve the equations (7) [17] except some very special circumstances. From the point of view of the well-known Input to State Stability (ISS) theory [2,7], to globally stabilize the nonlinear system (3), the differential equations (7) should satisfy the following relationships
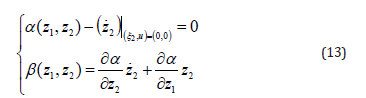
For the purpose of clarity, the equations (13) can also be rewritten as
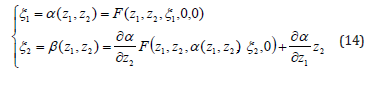
This means the subsystem (z1,z2) of (12) is zero-input stable (or free dynamics stable). Since the first equation of (14) is a nonlinear algebraic equation with respect to the single unknown variable ξ1 , it is straightforward that the equation (14) will be explicitly solvable for some special cases. On the basis of the relationships (14), Olfati-Saber [7] presented the “Fixed-Point Law” for stabilizing a class of nonlinear systems. It is worth noting that the differential equations (7) depict a surface in the state space (z, î )∈R4 , but the equation (14) is just a curve (invariant manifold) on the surface. Therefore, the non-triangular nonlinear systems that can be dealt with by the ISS theory are also limited to some very special cases. In the next section, it is shown that the fractional-power-based nonsmooth but continuous controllers can globally stabilize a class of highly nonlinear systems.
2. Robust controller based on the fractional-power feedback
Motivated by the relevant works [7,8, 12-16], in this section, the design of the robust controllers based on the fractional-power feedbacks is investigated to stabilize a class of non-triangular nonlinear systems. For a more general class of nonlinear systems comprising the nonlinear system (3), we present a theorem as follows.
Theorem 2: Consider the non-triangular nonlinear system

Proof: Due to the special cascade form of the linear part in the nonlinear system (15), we use “nearly” a standard backstepping procedure [1] to analyze the stability of the closed-loop system (15)-(16), and the Lyapunov function candidate is constructed by applying the powerful “adding a power integrator” technique presented in [12].
Now let’s firstly consider the subsystem ξ1, and select a
corresponding Lyapunov function candidate 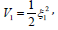 , the time derivate of V1 can be written as
, the time derivate of V1 can be written as

Refer to the Lemma 3 presented in the Appendix of the paper, it is easy to show that W1 >0 for all ξ2 ≠α1 , then the time derivate of V2 can be written as
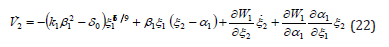
Now let’s estimate the bounds of the last three terms in righthand side of (22). Using the Lemma 1 and 2 in the Appendix of the paper, it is not difficult to show that the second term of the righthand side of (22) satisfies
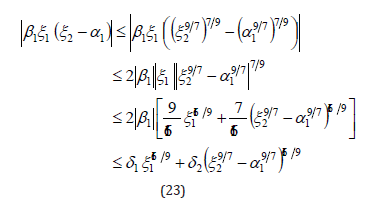
where δ1>0 and δ2>0 are two constants. The third term of the right-hand side of (22) can be expressed as
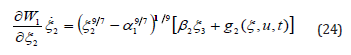
The fourth term of the right-hand side of (22) satisfies
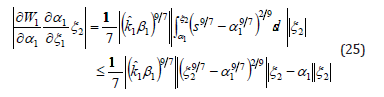
Once more, by applying the Lemma 1 and 2 of the appendix, the inequality (25) follows that
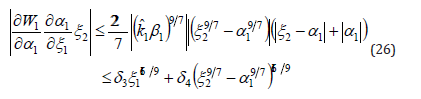
where δ3>0 and δ4>0 are two constants too. Substitute the inequalities (23)-(26) into (22), we obtain
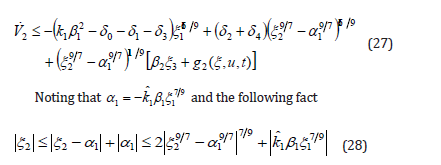
then the last term of the right-hand side of (27) satisfies
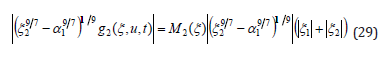
Due to the Lemma 1 and 2 in the appendix, it follows that
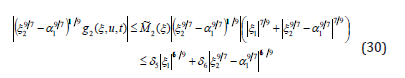
where δ5>0 and δ6>0 are two constants. Thus the inequality (27) can be written as

Proceeding along similar lines of the derivation of the second step given above, for the subsystem (ξ1,ξ2,ξ3), one can select the new Lyapunov function candidate.

where k4>0, δ2>0 are two constants. Then it is not difficult to show that the time-derivate of V4 satisfies following inequality
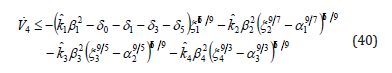
On the other hand, the Lyapunov function candidate given by (37) satisfies the inequality
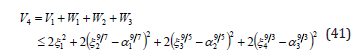
Therefore, by applying the inequality (A1) of the Appendix, it is easy to show that there exists a sufficiently large constant k > 0 such that the following inequality holds.
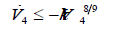
According to the Lemma 4 provided in the appendix of the paper, we complete the proof.
Remark 2: The crucial tools used in the proof of the theorem 2 are the inequalities (A1)-(A4) provided in the Appendix. With the help of the “adding a power integrator” technique, the Lyapunov function and the controller can be constructed step by step, which is analogous to a standard backstepping procedure. However, it is different from the standard backstepping procedure since the internal virtual controllers αi , i =1,2,3 are not smooth, i.e. αi∈C0 . So we have to construct the C1 function Wi , i =1,2,3 and to estimate the bounds of the induced differential terms of dWi dt in every step, such that the internal error associated with the preceding state variable can be involved in the followed virtualcontrollers.
Remark 3: We want to mention that Lemma 4 provided in the Appendix was firstly presented in [11], and it provides the foundation of synthesizing the controllers by fractional-powerbased feedbacks. In the literature [12] presented by Qian and Lin, the “adding a power integrator” technique is wisely used to designing the finite-time stabilizing controllers (FTSCs) for a class of nonlinear systems with strict feedback forms. In the relevant literatures [13] and [14], Hong et al. use a different approach from that of [12,15,16] to design the FTSCs. In this paper, we follow the approach presented in [12,15] since the Lyapunov function and the FTSCs can be simultaneously constructed with the help of the “adding a power integrator” technique. In [16], a FTSC is designed for linear systems by applying the approaches presented in [12] and [15]. In the present paper, we extend the approach of designing the FTSCs to a class of nonlinear systems with non-triangular forms.
Remark 4: It is noteworthy that the selections of the fractionalpowers for the FTSC (16) is not exclusive, such as that does in the relevant literatures [11] and [12,15]. It is straightforward that there exists a set of constants ki>0, i =1,...,4 , such that the following family of controllers.
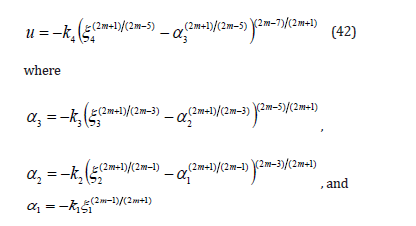
for all m ≥ 4 , can globally stabilize the non-triangular nonlinear systems (15) in finite settling time. The controller (42) can be regarded as a generalization of the controller (16).
Remark 5: For the following general non-triangular nonlinear system with single input
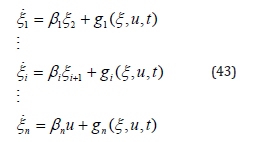
the corresponding FTSCs can be given as follows by properly selecting the parameters k i n i > 0, =1,2, of the feedbacks.
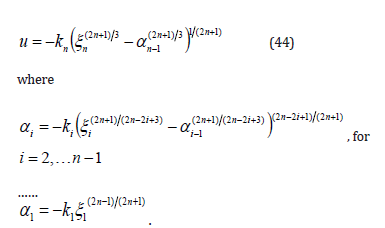
Proceeding along similar lines as in the proof of theorem 2, the controllers (42) and (44) can be constructed without any difficulties.
An example of applications
In this section, the benchmark SISO non-triangular nonlinear system, Ball-and-Beam (B&B) system is employed to numerically verify the robust stability of the presented controller (16). There are two types of the mechanisms of the B&B systems shown by the relevant literatures [7,8,18-21]. One type of them is illustrated in Fig.1, which is also investigated in this paper. The other type is based on the four-bar mechanisms of crank-linkage [18-20], of which the swing-link (as the beam) is used to drive the ball.

As that shown in the Figure 1, m is the mass of the ball, I1 and I2 denote the inertia of the beam and ball respectively, x and θ are the generalized coordinates of the mechanism, and d is the distance between the center of the ball and the axis of the pivot along the vertical direction of beam. Then the dynamics of the system can be given by
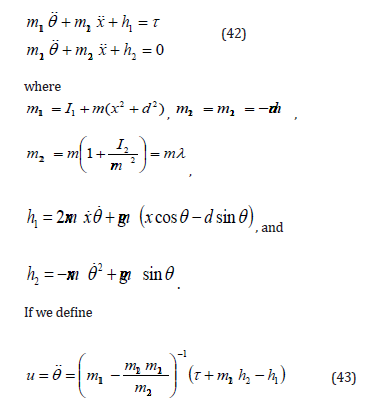
to be the new input, then the dynamics equation (42) can be written as
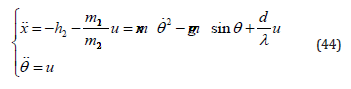
Using the global coordinate transformations
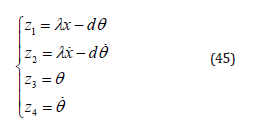
the dynamics of (44) can be expressed as the form in state space
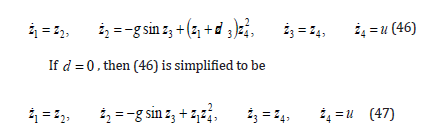
The dynamics given by (47) was commonly used in the relevant researches [8,19,21]. Stabilization of the B&B system with more general dynamics (46) was also studied in [7], but the controller was not clearly presented there. Due to the nonlinear term related to z24 in (46) and (47), the nonlinear systems under consideration are in a non-triangular form. In the present paper, the acceleration of gravity is given to be g =1(m/s2 ), which means the system working in a weak gravity flied. Thus, the disturbances caused by the nonlinear terms about the z24 ins (46) and (47) relatively enhanced.
To globally stabilize the nonlinear systems (46) and (47), it is necessary to transform the systems into the normal form of (15). Towards the end, we present following proposition.
Proposition 1: By the following coordinate transformation
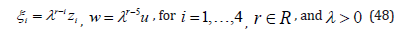
the nonlinear systems (46) and (47) can be changed to the normal form (15).
Proof: By applying the coordinate transformation (48), it is easy show that the nonlinear system (46) can be rewritten as
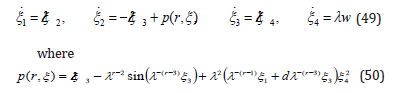
Thus, the perturbation term (50) is parameterized by the pairs (λ, r) . Since (48) is a global diffeomorphism, for all fixed constant λ > 0 and a feasible state z (t), i =1,,4 i of the system, there exists a real number r∈R and 0 0 M > , such that following inequality holds
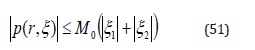
This completes the proof.
Remark 6: It is shown in relevant literatures [7, 8] that the controllers based on the saturated feedbacks with low gains can globally stabilize the nonlinear system (47). The fact is that the growth of the perturbation term p(r,ξ ) should be limited so that the nonlinear term in (47) satisfies the following relationship.

where O(⋅) denote the big Landau symbol. Hence, for all fixed λ > 0 , the boundary of the perturbation term p(r,ξ ) can be limited to satisfies the inequality (51) by adjusting the real parameter r∈R . For instance, if we select λ ∈(0,1) , then a smaller r∈R will help to limit the perturbation term in a given bounds for the state variables with large errors, while a larger r∈R is helpful for reducing the settling time for the of the state variables with small errors.
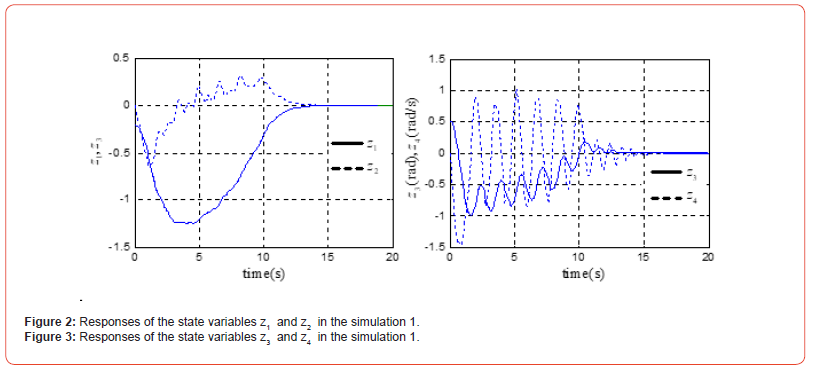
Simulation 1: For the system (47)( d = 0 ), given the initial state to be (z1,z2,z3,z4)=(-0.2,0,π / 6,0), the parameters of the controller (16) are selected to be (k1,k2,k3,k4)= (0.5,1,2,3) , and then the simulation results are illustrated in Figure 2 and Figure 3.
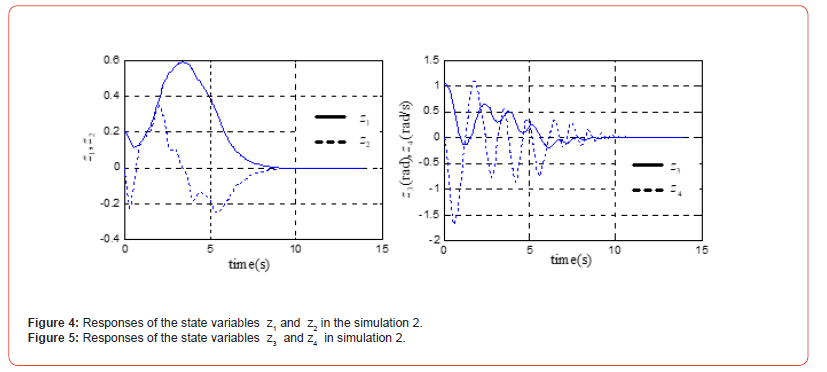
Simulation 2: For the system (46)( d = 0.7 ), the initial state of the system is given by (z1,z2,z3,z4)=(0.2,0,π / 3,0) π , while the control parameters are not changed, namely (k1,k2,k3,k4)= (0.5,1,2,3) , then the simulation results are plotted in the Figure 4 and Figure 5.
Conclusions
It is shown in the present paper that the non-smooth but continuous feedback is potentially an effective way for robustly stabilizing a class of highly nonlinear systems with nontriangular form. A chain of integrators perturbed by a vector field characterizes the systems considered in this paper. We show the considered highly nonlinear systems can be globally stabilized to the origin in finite settling time. Through the B&B system, we also show that a class of nonlinear systems with non-triangular form can be transformed into the perturbed linear systems, and the perturbation terms can be limited in the given bounds by adjusting the introduced scale parameters of the transformation. Then the B&B system can be globally stabilized by the presented FTSCs.
Appendix


where the “(A3)” on the “ ≥ ” indicates by applying the inequality (A3).
Lemma 4[11,15,16]: For the non-Lipschitz autonomous
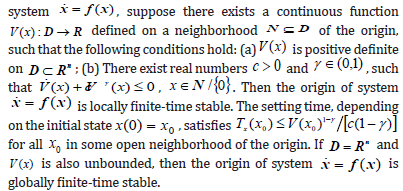
Acknowledgements
None.
Conflicts of Interest
None.
References
- MKrstić, I Kanellakopoulos, P Kokotović (1995) Nonlinear and adaptive control design. New York: John Wiley & Sons, Inc.
- R Sepulchre, M Janković, P Kokotović (1997) Constructive nonlinear control. London: Springer-Verlag.
- AR Teel (1996) A nonlinear small gain theorem for the analysis of control systems with saturation. IEEE Transactions on Automatic Control 41(9): 1256-1270.
- M Krstic (2004) Feedback linearizability and explicit integrator forwarding controllers for classes of feedforward systems. IEEE Transactions on Automatic Control 49(10): 1668-1682.
- R Olfati Saber (2002) Normal forms for underactuated mechanical systems with symmetry. IEEE Transactions on Automatic Control 47(2): 305-308.
- HJ Sussmann, P Kokotović (1991) The peaking phenomenon and the global stabilization of nonlinear systems. IEEE Transactions on Automatic Control 39: 2411-2425.
- R Olfati-Saber (2001) Nonlinear control of underactuated mechanical systems with application to robotics and aerospace vehicles. Massachusetts Institute of Technology, Doctor Dissertation.
- R Sepulchre (2000) Slow peaking and low-gain designs for global stabilization of nonlinear systems. IEEE Transactions on Automatic Control 45(3): 453-461.
- A Levant (2007) Principle of 2-sliding mode design. Automatica 43: 576-586.
- Y Hong (2001) H∞ control, stabilization, and input-output stability of nonlinear systems with homogeneous properties. Automatica 37: 819-829.
- Sanjay P Bhat, Dennis S Bernstein (2000) Finite-Time Stability of Continuous Autonomous Systems. SIAM Journal of Control and Optimization 38(3): 751-766.
- C Qian, W Lin (2001) A Continuous Feedback Approach to Global Strong Stabilization of Nonlinear Systems. IEEE Transactions on Automatic Control 46(7): 1061-1079.
- Y Hong (2002) Finite-time stabilization and stabilizability of a class of controllable systems. Systems & Control Letters 46: 231-236.
- Y Hong, J Wang , Z Xi (2005) Stabilization of uncertain chained form systems within finite settling time. IEEE Transactions on Automatic Control 50(9): 1379-1384.
- X Huang, W Lin, B Yang (2005) Global finite-time stabilization of a class of uncertain nonlinear systems. Automatica 41: 881-888.
- G He, Z Geng (2012) Finite-time stabilization of a comb-drive electrostatic microactuator. IEEE/ASME Transactions on Mechtronics 17(1): 107-115.
- SG Krantz, HR Parks (2013) The Implicit Function Theorem, History, Theory, and Applications. Boston: Springer-Verlag.
- MT Ravichandran, AD Mahindrankar (2011) Robust stabilization of a class of underactuated mechanical systems using time scaling and Lyapunov redesign. IEEE Transactions on Industrial Electronics 58(9): 4299-4313.
- L Márton, AS Hodel, B Lantos, JY Hung (2008) Underactuated robot control: comparing LQR, subspace stabilization, and combined error metric approaches. IEEE Transactions on Industrial Electronics 55(10): 3724-3730.
- F Andreev, D Auckly, S Gosavi, L Kapitanski, A Kelkar, et al. (2002) Matching, linear systems, and the ball and beam. Automatica 38: 2147-2152.
- R Ortega, MW Spong, FG Estern, G Blankenstein (2002) Stabilization of a class of underactuated mechanical systems via interconnection and damping assignment. IEEE Transactions on Automatic Control 47(8): 1218-1233.
-
Guangping He*, Junjie Yuan, Mengying Zhang, Lei Zhao and Quanliang Zhao. Robust Stabilization of a Class of Non-Triangular Nonlinear Systems. On Journ of Robotics & Autom. 2(1): 2023. OJRAT.MS.ID.000529.
-
Spontaneous femur fracture, Thyroid cancer, COVID-19 vaccine, Energy, Diet, Acupuncture, Traditional Chinese medicine, Homeopathy, Hippocrates
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






