 Research Article
Research Article
Some Analytical Grad-Shafranov Solutions in General Relativity: The Separation of Variables and the azimuthal-Angle Dependence
Orchidea Maria Lecian, Sapienza University of Rome, Rome, Italy
Received Date: November 27, 2023; Published Date: January 22, 2024
Abstract
Some new GrisShafranov solutions of spherically symmetric stationary space- times in General Relativity are analytically written in the chosen validity range. The Grad-Shafranov equations are proven to be solved at different orders of the powers of the grr component of the metric tensor for the Schwarzschild space- time, and for the generalized Schwarzschild spacetimes (i.e. the Schwarzschild spacetimes with a linear term, the Schwarzschild spacetimes with a cosmological constant, the Schwarzschild spacetimes with a linear term and a cosmological constant, the Mannheim-Kazanas-inspired spacetimes, the Bardeen-inspired spacetimes, etc.).
The assumption of separation of variables is newly formulated. The new General-Relativistic characterization and the new Astrophysical qualifications are outlined.
Introduction
The Grad-Shafranov in spherical coordinates for Astrophysical objects is present in [1], where introductory analytical study of winds and jets of compact astrophysical objects and stars is provided with in [1]. The analysis of the 3 d General-Relativistic simulations revealed azimuthal instabilities [2]. Further behaviors are described in [3]. The solution of the GS equation is demonstrated to comprehend 5 (’essentially’).
Arbitrary functions: F the mass conservation, G the perfect electrical conductivity, H the conservation of angular momentum, J the conservation of energy (Bernoulli constant) and S conservation of energy [4].
As recalled in [4], the GS equation is demonstrated after the absence of flow for F = G = 0. Differently, in the Generalrelativistic case, the dependence on the azimuthal- angle variable and that on time are neglected in [5]; in [5] the functions G and F are displayed. In the present analysis, a different approach is chosen with respect to [4] and to [5] to take into account the qualities of the General-Relativistic system. A validity range of the General-Relativistic analysis is chosen, according to the features of the stress-energy tensor in the chosen neighborhood of the blackhole. The dependence on the azimuthal-angle variable is here newly considered. Furthermore, the solutions of the Grad-Shafranov equations are newly proven to be solved at the different orders in the rr g component of the metric tensor in the chosen spherically-symmetric stationary spacetimes, and the instances are taken from their series expansions within the validity range of the solutions; more in detail, not only the Schwarzschild spacetime is taken into account: the result are newly proven to hold in a new different way also the generalized Schwarzschild spacetimes, such as those involving a linearterm in the rr g , a cosmological-constant term, Mannheim- Kazanas-inspired spacetimes the Bardeen-inspired spacetimes etc. After the new hypothesis of separation of variables, the new analytical solutions are newly spelled out explicitly under suitable assumptions; the assumptions are those qualifying the Astrophysical qualities of the system. The research guidelines of the further Astrophysical qualifications of the solutions are outlined.
The Generalized Grad-Shafranov Equation in General Relativity: Developments of the Mobarry- Lovelace formalism
The Generalized Grad-Shafranov Equation in General Relativity in the Mobarry- Lovelace formalism around a Schwarzschild blackhole can be solved in spherical- coordinates systems and in cylindrical-coordinate systems. In the following, the spherical coordinates will be chosen to newly solve analytically the Grad-Shafranov equations of a stationary, spherically symmetric, ideal plasma flow around a Schwarzschild blackhole and around a generalized Schwarzschild blackhole (issued as from the conditions expressed in Section 3). The Grad- Shafranov equations are here written in spherical coordinates as

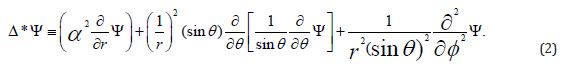
The Schwarzschild spacetimes and the generalized Schwarzschild spacetimes
The generalized Schwarzschild spacetimes are expressed after the line element.
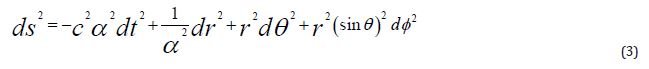
In Eq. (3), the object α can be referred to the Schwarzschild spacetime, as well as to generalized Schwarzschild spacetimes, expressed after the line element.

The Grad-Shafranov equation in General Relativity: Astrophysical scenarios
The aim of this section is to study the solutions of Eq. (1) in a General- Relativistic spacetime.
Differently from [5], the functional dependence of the poloidal flux function on the azimuthal angle φ is here newly considered, as motivated from The Schwarzschild spacetime is chosen as a first instance of investigation.
A range of validity of the wanted solution Ψ(r,θ ,φ ) from Eq. (1) is chosen as

General-Relativistic scenarios
The metrics chosen to be dealt with within the investigation are spherically- symmetric stationary metrics. As an instance, the Schwarzschild spacetime is considered. The results are straightforward extended to the generalized Schwarzschild spacetimes, i.e. such as the Schwarzschild deSitter spacetimes, the Schwarzschild antideSitter spacetimes, the generalized Schwarzschild space- times with a linear term, the generalized Schwarzschild spacetimes with a linear term and a cosmologicalconstant term, the Mannheim-Kazanas spacetimes, the Bardeen-inspired metrics, and further generalizations. The Grad-Shafranov equations will therefore newly decomposed according to the powers of the g(rr) component and will be newly solved accordingly.
To explain the procedure, the first terms of the series expansions are listed:
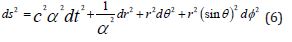
will be considered.
The results must be studied for the generalized Schwarzschild metric.

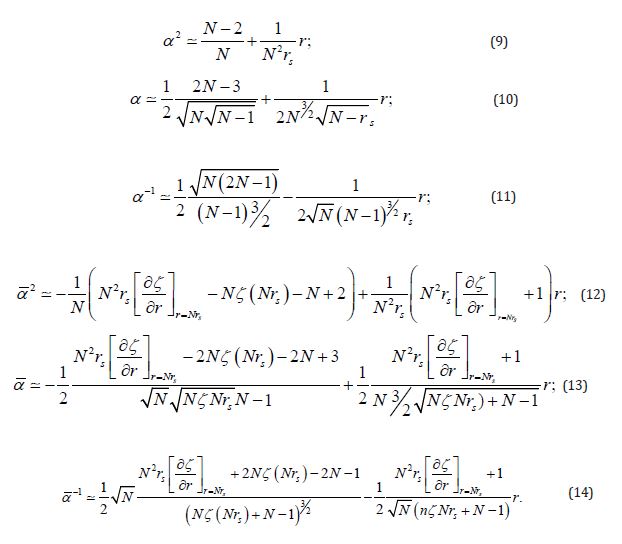
The validity range chosen according to Eq. (5) allows one to series-expand the grr component around the multiples S Nr of the Schwarzschild radii. The series expansions must be assured to hold. The validity range will be therefore expressed as
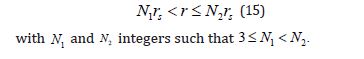
The validity range Eq. (15) is chosen in a way such that the terms of the series expansions of the powers of the grr component do not overlap.
New separation of variables of the solution of the Grad-Shafranov equation
The range of validity Eq. (5) is chosen such that the solution Ψ(r,θ ,∅) be achieved after the new separation of variables, i.e. such as
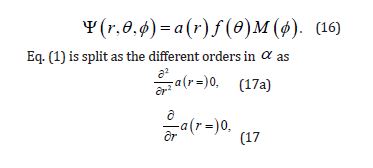
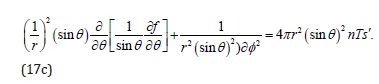
Some new solutions of the Grad-Shafranov equation in generalized Schwarzschild spacetimes
The solution is calculated at the different orders in α from Eq. (1) under the condition.

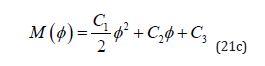
where the integration constants A, , 1C , 2 C , 3 C , have been defined; to these purposes, the constant C1 necessitates further General-Relativistic characterizations (as it will be done in the following), while the initial condition 0 θ must be given.
It is momentous to remark that the new dependence on the variable φ is a General-Relativistic quality, which has newly been discovered in the case of Schwarzschild spacetime and in those of generalized Schwarzschild spacetimes, as it had never been pointed out in the present literature.
General-Relativistic characterization and Astrophysical qualifications
From the obtention of the solutions Eq.’s (21), the following characterizations are required. The new limits 2 F /α and G / Alpha2must be newly considered. As an example, as far as the conservation of particles’ surface function is concerned, the new

The integration constant C1 is chosen accordingly.
Outlook
In [11], the Grad-Shafranov solutions are considered in the case of the Schwarzschild spacetime; in particular, the cylindrical coordinates are chosen. The analytically expression of the solution of the Grad-Shafranov equations in the Keplerian case are analytically solved: as, in the Keplerian case, 1 rr g ≡ and 1 tt g ≡ , the solutions are not split according to any series expansion of the components of the metric.
In [12], the MHD qualities of a jet related within a spinning blackhole spacetime are studied: the electromagnetic fields and the fluid motion are ruled by the Grad-Shafranov equation and the J (Bernoulli) equation, respectively; a steady and axisymmetric jet in the Kerr spacetime (characterized as after the items of investigation [13]) is studied: as a methodology, the bulk velocity in the fluid description is posed as vanishing throughout the loading zone, as it diverges at the Kerr blackhole horizon; as a result, slow flow acceleration and flow velocity stratification are found within the regions 105 gravitational radii from the central blackhole object.
In the case of the Kerr spacetimes, the Grad-Shafranov equations in the case of a disk were integrated numerically in [13]. In the present analysis, the Grad-Shafranov equations are considered in spherically symmetric, stationary spacetimes, such as the Schwarzschild spacetime and the generalized Schwarzschild spacetimes. The validity range of the solutions is chosen according to the qualities of the given spacetimes. The Grad-Shafranov equations are demonstrated to be split according to the different powers of the rr g components of the metric tensor; the validity range must be therefore one for which the series expansions of the powers of the rr g component of the spacetimes metrics do not overlap. The solution of the Grad-Shafranov equations is rewritten under the hypotheses of separation of variables and solved analytically. The new constraints are found.
Acknowledgment
None.
Conflict of interest
No conflict of interest.
References
- VS Beskin (2005) MHD Flows in Compact Astrophysical Objects. Springer- Verlag Berlin Heidelberg 2010 [Axisymmetric and stationary Astrophysics Theory, Moscow Fizmatdit].
- KI Nishikawa (2002) 3-D General Relativistic MHD Simulations of Generating Jets, Proc. Oxford Radio Galaxy Workshop, Ed.’s R. Laing, K. Blundell, ASP Conference Series, San Francisco: PASP.
- F Mertens, AP Lobanov, RC Walker, PE Hardee (2016) Kinematics of the jet in M87 on scales of 100-1000 Schwarzschild radii, A&A 595: A54.
- RVE Lovelace, C Mehanian, CM Mobarry, ME Sulkanen (1986) Theory of axisymmetric magnetodynamic flow: disks, The Astrophysical Journal Supplement Series 62: 1-37.
- C Mobarry, RV E Lovelace (1986) Magnetohydrodynamic flows in Schwarzschild geometry. The Astrophysical Journal 309(2), 455-466.
- DA Uzdensky (2005) Force-Free Magnetosphere of an Accretion Disk-Black Hole System. II. Kerr Geometry 620: 889.
- W Junor, JA Biretta, M Livio (1999) Formation of the radio jet in M87 at 100 Schwarzschild radii from the central black hole, Letters to NATURE 401: 891-892.
- S Koide, K Shibata, T Kudoh (1998) General Relativistic Magnetohydrodynamic Simulations of Jets from Black Hole Accretion Disks: Two- Component Jets Driven by Nonsteady Accretion of Magnetized Disks, The Astrophysical Journal, 495: L63-L66.
- K Hada, et al. (2013) Innermost collimation structure of the M87 jet down to ten Schwarzschild radii, The Astrophysical Journal 775(1). M Kino, et al. (2014) Relativistic electrons and magnetic field of the M87 jet on ten Schwarzschild radii scale, The Astrophysical Journal 786(1).
- DA Uzdensky, (2004) Force-free magnetosphere of an accretion disk-Black hole system. 1. Schwarzschild geometry, Astrophys. J 603: 652-662.
- L Huang, Z Pan, C Yu, (2020) Toward a Full MHD Jet Model of Spinning Black Holes. II. Kinematics and Application, The Astrophysical Journal, 894: 45-57.
- K Asada, (2014) Discovery of Sub- to Superluminal Motions in the M87 Jet: An Implication of the Acceleration from Sub-relativistic to Relativistic Speeds 781: L2.
- R Luest, A Schlueter, Kraftfreie Magnetfelder (1954) Zeitschrift f¨ur Astrophysik 34: 263
-
Orchidea Maria Lecian*. Some Analytical Grad-Shafranov Solutions in General Relativity: The Separation of Variables and the azimuthal-Angle Dependence. Onl J of Conf Procee. 1(1): 2024. OJCP.MS.ID.000502.
-
Electrical Conductivity, Arbitrary Functions, Azimuthal Angle, Grad-Shafranov, Schwarzschild Radius, Antidesitter, Hypothesis, Axisymmetric, Cosmological, Bardeen-inspired metrics
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
- Abstract
- Introduction
- The Generalized Grad-Shafranov Equation in General Relativity: Developments of the Mobarry- Lovelace formalism
- Conclusion
- The Schwarzschild spacetimes and the generalized Schwarzschild spacetimes
- The Grad-Shafranov equation in General Relativity: Astrophysical scenarios
- General-Relativistic scenarios
- New separation of variables of the solution of the Grad-Shafranov equation
- Some new solutions of the Grad-Shafranov equation in generalized Schwarzschild spacetimes
- Outlook
- Acknowledgments
- Conflict of Interest
- References






