The Non-linear Constitutive Modelling of Fibre Reinforced Composites

The successful application of fibre reinforced composites (FRPs) in aerospace and automotive industries brings increasing requirements of understanding the failure behaviour of this material. However, the predictions of the mechanical response of composites were significantly affected by the non-linear behaviour of the material. This nonlinearity plays a critical part in accurate determination of the stress states before failure occurs. Therefore, thorough understanding of the non-linear stress-strain response under different stress conditions were essential.

Fibre reinforced composites (FRPs) usually exhibits linear elastic mechanical response along the fibre direction, while highly nonlinear stress-strain behaviour was reported under shear loading for carbon and glass fibre reinforced polymer composites [1], certain degree of nonlinearity was also detected on the transverse direction. Chang and Chang [2] simulated the progressive damage of open hole composites and suggested that the including of shear nonlinear law plays an crucial part in accurately predict the tensile response of laminates.

To characterize the nonlinear behaviour of unidirectional (UD) laminates under in plane shear, Hahn and Tsai [3] proposed a one parameter polynomial shear stress-strain relationship:

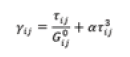
where, γij and τij are the shear strain and stress, respectively, Gij⁰ is the initial shear modulus, α is the material parameter that can be determined from experimental results

Several works have applied this model for shear damage analysis of composite materials. Chang and Lessard [4] used the Hahn-Tsai model to investigate the nonlinear response of open-hole laminates subjected to compressive loads. Dano et al. [5] utilized this model to taken into account the nonlinear shear response during the analysis of laminates with fastened joins. However, disadvantages were also reported during the application of this nonlinear relationship: (1) the model was developed representing the nonlinear elastic shear behaviour, hence unsuitable for composite materials with large nonlinear shear deformation; (2) the form of the function uses stress to express strain makes it difficult to integrate into FE models.

Mohseni and Li [6] modified the three-rail shear fixture to preform loading-unloading cycle tests to study the nonlinear shear response of unidirectional composites. Experimental results suggest that the in-plane shear nonlinearity is composed of elastic, plastic and viscous shear deformation as well as shear hardening. Lou and Schapery [7] proposed a nonlinear viscoelastic constitutive relationship for unidirectional glass fibre composites based on the thermodynamic theories. The nonlinear viscoelastic parameters of this material were represented by the average octahedral shear stress of the matrix. Papanicolau et al. [8] applied Schapery’s constitutive law to unidirectional composites under off-axis loading conditions. The nonlinear viscoelastic response of UD composite with three different fibre orientation angles (90°, 75° and 60°) were investigated. Results indicates that as the decrease of fibre orientation angle, parameters of the constitutive equation increase.

Van Paepegem et al. [9] conducted monotonic and cyclic tension tests on ±45° glass fibre reinforced polymers to characterise the in-plane shear behaviour of this material. The obtained nonlinear shear stress-strain relationship was identified as a permanent shear deformation and shear damage combination. A material model was built by Van Paegegem et al. [10] to simulate the permanent shear nonlinearity and shear modulus degradation of unidirectional and cross-ply composites. However, the effect of transverse stress on the evolution of shear damage was observed yet not analysed within this material model.

Totry et al. [11] conducted monotonic and unloading-reloading cycle tests on cross ply V-notch specimens to inspect the shear damage mechanisms. Shear deformation parallel and perpendicular to the loading direction was characterised, the overall shear performance was contributed by both elastic and plastic shear deformation. Totry et al. [12] further investigated the effect of properties of fibre, matrix and interface on the shear nonlinear response of composite materials through in-plane shear tests of cross-ply specimens as well as simulations of micromechanical models. Conclusions were draw that the matrix yield strength and interface strength has dominated the shear nonlinearity.

Laux et al. [13] developed a plasticity model to describe the nonlinear behaviour of UD composites. The non-associative flow rule and Dracker-Prager yield function was integrated in the model to simulate the biaxial stress state responses. To characterise the material parameters in the model, a modified Arcan fixture was developed to produce tension/shear and compression/shear combined stress states.

McCarthy et al. [14] model the nonlinear shear behaviour by fit the experimental stress-strain curves using cubic spline interpolation. High accuracy was reported when simulating the shear nonlinear response of composite materials, whereas the nonlinear transverse behaviour was observed in experiments yet not taken into consideration.

To further understand the effect of nonlinearity in different directions, Sun and Chen [15] proposed an one parameter plastic material model, in where the transverse and in-plane shear stresses were used to express the quadratic yield function of unidirectional fibre reinforced composites. The stress-strain relationship was deduced from the effective stress and effective plastic strain relationship that fitted from off-axis tension tests. Yokozeki et al. [16] reported an existence of off-axis tension and compression asymmetry in carbon/epoxy composites. They modified the Sun and Chen model by adding a Drucker-Prager model [17] like parameter to characterise the different nonlinear behaviours in off-axis tension and compression. Experimental stress-strain relationships of off-axis compression specimens with different angles were used to fit into one effective stress-strain curve. However, the adopted associative flow rule and yield functions can bring non-physical transverse plastic strains when analysing the off-axis specimens under tension and compression.

Ladeveze and Le Dantec [18] suggested that the shear nonlinearity was generated from matrix plasticity and fibre/matrix interface debonding, while the transverse nonlinear response was supposed to be caused by matrix plasticity and microcracking. Hence, they further improved the Sun and Chen model [15] by couple the plasticity model with matrix microcracking and matrixfibre debonding induced damage, the anelastic shear strains was characterised by effective stress and isotropic hardening was assumed. However, the model described requires extensive experiments to calibrate the materials parameters. Payan and Hochard [19] calibrated the Ladeveze and Le Dantec [18] model by static tension and tension/tension fatigue tests of ±45° carbon fibre epoxy specimens. The model was simulated to verify the fatigue shear nonlinear behaviour of the cross-ply laminates. Donadon et al. [20] simplified the Ladeveze and Le Dantec [18] model, the new nonlinear shear damage model decomposes the shear strain into elastic and damage strain components. Similarly, the damage strain was separated into elastic damage strain and in-elastic damage strain. The shear stress was expressed by an experimentally fitted cubic polynomial of strain and provides accurate predictions of composites under shear loading conditions. Egan et al. [21] applied this shear model into finite element simulation of bearing damage of composite joints, good correlation with experimental results was reported. Chen et al. [22] also combined this shear nonlinear law with plasticity damage model to simulate the progressive damage of open hole composite plates. Although this model shows simplicity and efficiency, it fails to represent the matrix cracking and fibre/matrix interface debonding mechanisms. O’Higgins et al. [23] investigated the influence of matrix plasticity and sheartransverse coupled plastic response on the Ladeveze and Le Dantec [18] model’s predictions. Results indicate that the absence of plasticity has little effect on the simulation accuracy, while the shear-transverse coupled nonlinearity act as an important material characteristic.

Vogler et al. [24] and Hsu et al. [25] investigated the transverse compression and shear nonlinear responses of AS4/PEEK composites experimentally and numerically. An experimental study comprised of in-plane shear, transverse compression and shear/compression combined biaxial stress states were conducted. Inspection of the results show that both directions have significant nonlinear deformations, interaction between shear and transverse compression stress-strain nonlinearity was also reported. Micromechanical models of the fibre reinforced composite were established with an elastic-visco-plastic model implemented to represent all inelastic responses and damages induced nonlinearity of the matrix. Simulations of the unidirectional composite under pure shear, transverse compression and shear/compression combined biaxial loadings were performed. Although the predictions of simple shear and compression nonlinear responses correlate well with experimental results, the proposed model cannot accurately predict both shear and transverse compression nonlinearity under biaxial stresses. The complex interaction mechanisms between shear and transverse nonlinearity needs in-depth study.

Most researches on the nonlinear shear modelling of fibre reinforced composites are focused on the two-dimensional stress state condition. Fewer work has been extended into threedimensional modelling of the nonlinear response of composite materials. The proposed three-dimensional nonlinear models bring in material parameters that require sophisticated experiments to calibrate.

Despite the good correlation between published nonlinear constitutive models with experiments, the variety of experimental methods was limited. Most material models were developed for analysing certain loading conditions and were verified with only a few groups of tests. The scarcity of experimental validations requires diverse testing methods to intensely investigate the nonlinear deformation mechanisms especially under biaxial stress states and different hydrostatic pressures.

Although the in-plane shear nonlinearity was thoroughly investigated through experiments and numerical modelling, the interaction between shear/compression or shear/tension combined stress states still lacks study. Based on the current researches, no agreement has reached on whether transverse stress has an effect on the shear nonlinear behaviour. Hence, further research on the coupling behaviour of shear/transverse direction nonlinearity are critical in help understanding the mechanisms of nonlinearity of fibre reinforced composites.

None.

No conflict of interest.

1. +-Hinton MJ, Kaddour AS, Soden PD (2004) Lamina Properties, Lay-Up Configurations And Loading Conditions For A Range Of Fibre-Reinforced Composite Laminates. Failure Criteria in Fibre-Reinforced-Polymer Composites: The World-Wide Failure Exercise, 1^st Edn, pp. 12.
2. Chang Fu-Kuo, Chang KY (1987) A Progressive Damage Model for Laminated Composites. Journal of Composite Materials. J Compos Mater 21(9): 834-855.
3. Hong T Hahn, Stephen W Tsai (1973) Nonlinear Elastic Behavior of Unidirectional Composite Laminae. Journal of Composite Materials 7(1): 102-118.
4. Chang FK, Lessard LB (1991) Damage Tolerance of Laminated Composites Containing an Open Hole and Subjected to Compressive Loadings: Part I—Analysis. Journal of Composite Materials 25(1): 2-43.
5. Dano ML, Gendron G, Picard A (2000) Stress and failure analysis of mechanically fastened joints in composite laminates. Composite Structures 50(3): 287-296.
6. Mohseni Shakib SM, Li S (2009) Modified three rail shear fixture (ASTM D 4255/D 4255M) and an experimental study of nonlinear in-plane shear behaviour of FRC. Composites Science and Technology 69(11-12): 1854-1866.
7. Lou YC, Schapery RA (1971) Viscoelastic Characterization of a Nonlinear Fiber-Reinforced Plastic. Journal of Composite Materials 5(2): 208-234.
8. Papanicolaou GC, Zaoutsos SP, Kontou EA (2004) Fiber orientation dependence of continuous carbon/epoxy composites nonlinear viscoelastic behavior. Composites Science and Technology 64(16): 2535-2545.
9. Van Paepegem W, De Baere I, Degrieck J (2006) Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part I: Experimental results. Composites Science and Technology 66(10): 1455-1464.
10. Van Paepegem W, De Baere I, Degrieck J (2006) Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part II: Model development and finite element simulations. Composites Science and Technology 66(10): 1465-1478.
11. Totry E, González C, LLorca J, et al. (2009) Mechanisms of shear deformation in fiber-reinforced polymers: experiments and simulations. International Journal of Fracture 158(2): 197-209.
12. Totry E, Molina-Aldareguía JM, González C, LLorca J (2010) Effect of fiber, matrix and interface properties on the in-plane shear deformation of carbon-fiber reinforced composites. Composites Science and Technology 70(6): 970-980.
13. Laux T, Gan KW, Dulieu-Barton JM, Thomsen OT (2019) A simple nonlinear constitutive model based on non-associative plasticity for UD composites: Development and calibration using a Modified Arcan Fixture. International Journal of Solids and Structures 162: 135-147.
14. McCarthy CT, O’Higgins RM, Frizzell RM (2010) A cubic spline implementation of non-linear shear behaviour in three-dimensional progressive damage models for composite laminates. Composite Structures 92(1): 173-181.
15. Sun CT, Chen JL (1989) A Simple Flow Rule for Characterizing Nonlinear Behavior of Fiber Composites. Journal of Composite Materials 23(10): 1009-1020.
16. Yokozeki T, Ogihara S, Yoshida S, Ogasawara T (2007) Simple constitutive model for nonlinear response of fiber-reinforced composites with loading-directional dependence. Composites Science and Technology 67(1): 111-118.
17. Drucker DC, Prager W (1952) Soil mechanics and plasticity analysis of limit design. Quarterly of Applied Mathematics 10(2): 157-165.
18. Ladeveze P, LeDantec E (1992) Damage modelling of the elementary ply for laminated composites. Composites Science and Technology 43(3): 257-267.
19. Payan J, Hochard C (2002) Damage modelling of laminated carbon/epoxy composites under static and fatigue loadings. International Journal of Fatigue 24(2): 299-306.
20. Donadon MV, Iannucci L, Falzon BG, Hodgkinson JM, De Almeida SFM (2008) A progressive failure model for composite laminates subjected to low velocity impact damage. Computers & Structures 86(11-12): 1232-1252.
21. Egan B, McCarthy MA, Frizzell RM, Gray PJ, McCarthy CT (2014) Modelling bearing failure in countersunk composite joints under quasi-static loading using 3D explicit finite element analysis. Composite Structures 108: 963-977.
22. Chen JF, Morozov EV, Shankar K (2012) A combined elastoplastic damage model for progressive failure analysis of composite materials and structures. Composite Structures 94(12): 3478-3489.
23. O’Higgins RM, Mccarthy CT, McCarthy MA (2012) Effects of Shear-Transverse Coupling and Plasticity in the Formulation of an Elementary Ply Composites Damage Model, Part I: Model Formulation and Validation. Strain 48(1): 59-67.
24. Vogler TJ, Kyriakides S (1999) Inelastic behavior of an AS4/PEEK composite under combined transverse compression and shear. Part I: experiments. International Journal of Plasticity 15(8): 783-806.
25. Hsu SY, Vogler TJ, Kyriakides S (1999) Inelastic behavior of an AS4/PEEK composite under combined transverse compression and shear. Part II: modeling. International Journal of Plasticity 15(8): 807-836.