Multiple Linear Regression Method for Deeper Analyses of Abrasive Tribological Behaviour of Engineering Materials

Tribology (friction, wear, lubrication) studies the elements made of different materials in relative motion. While the individual materials can be well characterized e.g. by their physical and chemical properties the description and prediction of the friction and wear behaviour is not an easy task. There is no uniform, analytical calculation method, because the behaviour of the structural materials depends on the operating conditions and the effects occurring during operation, thus, the tribological behaviour is system dependent. In order to have information about wear, friction and heat generation during operation, it is advisable to use the modelling method. The result of either mechanical or numerical modelling can help machine designers. The use of simplified models performed under laboratory conditions (DIN50322, testing category VI.) is very common, where relative comparison of friction materials is possible under fixed conditions. The laboratory tribotest equipments are usually suitable for online data collection, so that friction force, heat generation, wear and deformation can be continuously recorded during a sliding process. These datasets provide an opportunity not only for primary trend analysis of the measured quantities, but also for in-depth analysis of the relationships between tribological trends and material characteristics. Hundreds of articles have been published in the tribological literature where wear, surface deformation, or friction have been evaluated as a function of some material characteristics or simple combinations thereof. The first famous results e.g. in the field of abrasion wear, the wear estimates published by Lancaster in the late 1960s [1]. Not highlighting each work, overall the surface hardness (H), tensile modulus of elasticity (E) and tensile strength (R) were mainly in focus, as a function of which tribological processes, the friction and wear behaviour of materials were evaluated.

With the multiple regression method, on one hand, it is possible to statistically evaluate all material properties and the dimensionless numbers formed from them in a model. As a result of the method, the goodness-of-fit of the models for the friction, wear, heating and surface micro-geometry characteristics is not primarily important. Power functions or higher order polynomials may offer better approximation, but in the case of on-line dataflow in tribology one does not need extra high correlation (e.g. higher than 0.8-0.9), because the trends of the repeated measurements have to be clear and similar. On the other hand, by using higher order polynomials, the mixed parameters of the second or higher power models could cause physical information loss. The method shows what had an effect on the measured tribological characteristics at all, and the influencing factors can be ranked in a relative order. A detailed, recent literature source for this evaluation method is e.g. [2], where the abrasion sensitivity of engineering plastics is analyzed in the light of a large number of independent variables is available. In numerous previous tribology paper, it was verified that the functions of several variables, which describe the dependence of the factors were approximately linear, that is, for a dependent variable Y the following relation holds:

where n is the number of independent variables and X1,X2,…,Xn are the independent variables.

The method of least squares is the most common way to fit such a model to the measured data. To see which independent variable had the greatest effect on Y, one must consider the absolute value of the standardized (or beta) coefficients of the significant independent variables; the higher this value is, the greater the effect is.

Independent variable for the evaluation of on-line wear-, heat generation or friction curve, or change of surface roughness parameters can be the sliding distance, speed, load, the single material properties, and combined properties as e.g.

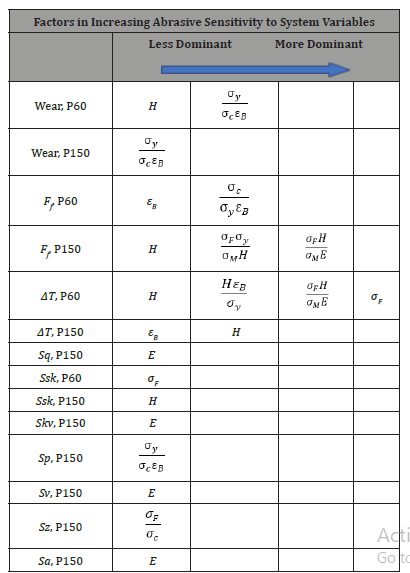
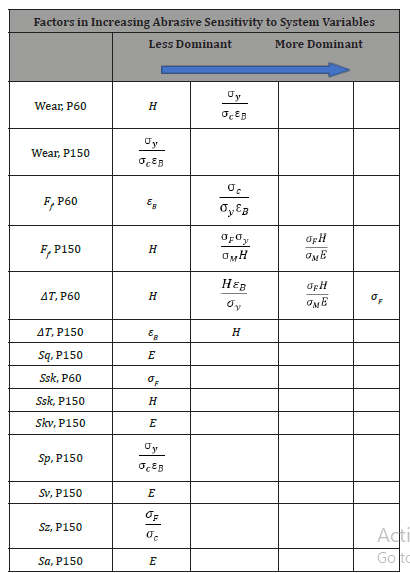
For metallic structures interesting dimensionless factor can be the ratio of Charpy impact strength measured at 20 °C and -40 °C. By means of the models’ calculation, such a kind of sensitivity evaluation of tribological process can be obtained, as it is shown in Table 1. Table 1 gives a relative ranking of the factors that had effect on the measured tribological feature. The introduced system was abrasive pin-on-plate with P60 and P150 standard clothes against engineering polymer pins. Wear (measured in mm), friction force (Ff), friction heat generation and some 3D surface roughness parameters can be connected to the material properties or their dimensionless combination on the base of multiple regression.

Table 1:Ranking the abrasive sensitivity to the system features [2].

None.

No conflict of interest.

1. Lancaster JK (1969) Abrasive wear of polymers. Wear 14(4): 223-239.
2. H Muhandes, Á Kalácska, L Székely, R Keresztes, G Kalácska (2020) Abrasive Sensitivity of Engineering Polymers and a Bio-Composite under Different Abrasive Conditions. Materials 13(22): 5239.