 Review Article
Review Article
Hydrothermal Ageing Impact & Damage Characterization for Polymeric Composites by means of Experimental Techniques
Farkhanda Afzal1*, Rukhsana Bibi2, Deeba Afzal3 and Faryal Chaudry3
1MCS, National University of Sciences and Technology (NUST), Islamabad, Pakistan
2University of the Lahore, Pakpattan Campus, Pakpattan, Pakistan
3University of the Lahore, Lahore Campus, Lahore, Pakistan
Farkhanda Afzal, MCS, National university of Sciences and Technology (NUST), Islamabad, Pakistan.
Received Date: November 12, 2019; Published Date: November 26, 2019
Abstract
Composite materials are nowadays extensively used in aerospace structures, off-shore platforms, automotive industry and many other high technology fields because of combination of excellent mechanical performance and light weight. For these reasons classical metal alloys are progressively replacing primary structural components by reinforced polymeric compo- sites. The aim of this research is to develop models to predict degradation in Polymeric Composite Materials under varying moisture conditions. This goal has been achieved by using a combination of experimental and numerical methods. Various experiments were carried out to characterize the moisture uptake and mechanical properties of number of different composite materials. In these research models were developed for predicting moisture concentration in the composite materials under recurrent moisture absorption and desorption conditions. The aim of this research is the development of modelling methodology for the prediction of degradation in polymeric composites subjected to fluctuating environmental service conditions.
Keywords: Hydrothermal ageing; Moisture diffusion; Fiber fracture; Fiber-matrix deboning; Unidirectional composites
Introduction
Polymer matrix carbon fiber composites are widely used in aerospace, automotive and civil industries due to their attractive properties, e.g., high strength-to-weight ratio, easy processing, excellent corrosion resistance and good thermal stability [1]. Despite the desirable properties of polymer matrix composites, one major disadvantage of them is their tendency to absorb water in humid environment, as most polymer matrices are highly polar [2]. Absorbed moisture dramatically degrades the composite performance.
Durability of composite materials is a primary consideration due to their sensitivity to environmental conditions, particularly combination of high temperature, humidity and stress [3]. Various environmental factors affect the durability of polymeric composites, such as temperature, moisture, fiber orientation, density, polarity of fiber, fiber volume fraction, ultra- violet radiation and diffusivity [4]. The two major factors influencing the strength are temperature and moisture. The effect of temperature may be observed in the form of variation in mechanical properties of a composite material [5]. Temperature variation may also affect the moisture diffusion rate through composites. Interface strength degradation may occur owing to deboning by moisture ingress, corrosion or weakening of material in the interphase [6]. The properties of the matrix (resin) can also change significantly during exposure to an aqueous environment, water can diffuse between fibers and the matrix, weakening or destroying the bond at the fiber/matrix interface [7,8]. The level of moisture absorption during specific period depends on the diffusion coefficient [9-11]. Characterization of the long-term response of composites due to moisture diffusion and understanding of the underlying failure mechanisms, such as plasticization, swelling, micro-cracking and modification of the chemical structure are important for developing methods to predict service life under severe hydro- thermal conditions [12-16].
Moisture diffusion under cyclic environmental conditions is described as structures may experience environmental variations and degradation during service life [17,18]. The testing methods used for determining the strength and effect of moisture diffusion on composites durability are studied [19, 20].
Hydrothermal conditioning may represent an important source of ageing and degradation, especially in polymeric-based composite laminates structures. Water diffusion may contribute to material properties degradation and leads to the development of an elastic strains, (defanelastic strain, which relating to the property of a substance in which there is no definite relation between stress and strain strains of hygroscopic nature), which contribute to the building of internal stress. High temperature may also responsible for material properties changes and for development of thermal stresses, leading possibly to damage onset and propagation [21,22].
Polymer resins highly filled with fibers or fabrics to improve their mechanical performance are generally known as polymer matrix composites (PMCs). The high level of filler material in composites is likely to lead to permeation and diffusion properties that differ significantly from unfilled or lightly filled materials. Composites tend to be used as thick sections, in addition they often laid up as laminates with interfaces between the layers contributing an important role in diffusion behavior. High performance structural PMCs are often made from thermosetting resins, such as epoxies that tend to be hydrophilic, filled with inorganic fibers (e.g. glass or carbon). Exposure to moisture may lead to degradation of the fib resin adhesion or degradation of the fibers themselves, weakening the composites. The orientation of the fibers is also highly affected by water ingression [23].
The moisture diffusion in polymeric composites and their effects on composites’ performance are highly complex issues. Their study involves, in at least, the discipline of polymer science and applied mechanics, where the former focuses on molecular-level interactions and the latter is concerned with mechanical response [22]. To begin with, polymers are highly complex materials that vary in structure and Physico-chemical properties, and polymeric composites adjoin a variety of fibers with extremely intricate fiber/ matrix interphases and interfacial bonding. The complexity is further compounded by the ingress of fluids of many kinds, which interact with the polymer, the fiber and the interphase matters within the composites [24].
The most common moisture transport mechanism in polymeric composites is through diffusion which is explained by Adamson [25] that transport of moisture in epoxy composites below Tg occurs in three stages. In the first stage, absorbed moisture occupies the free volume present in the form of ‘holes’ or voids. In the second stage, the absorbed moisture attacks the polymeric network sites resulted in the form of swelling and in the third stage, water finally enters the densely cross-linked region. The other common mechanisms are capillarity and transport through micro-cracks and voids. Many studies [26,27] have indicated that the mobility and solubility of small molecules in glassy polymers depend on the free volume present in the polymer. Molecules will absorb more readily and be more mobile in polymer matrix with high free volumes than in polymers with low free volumes. The free volume depends on the nature of the polymer and on the physical state of the polymer, including molecular orientation and physical ageing effects. The key concern associated with the mechanical performance of composites in the presence of fluids concern their dimensional stability, strength, fatigue response, and impact resistance. The kinetics of fluid absorption in solids has been studied first scientifically by Fick [28], among others the most significant contribution in this filed was done by Rogers [29], Comyn [30], Frisch [31], Stannett, Hopfenberg, and Petropoulous [32] and several books like Crank [33] and Ghez [34].
The effects of fluids (moisture) on the creep response of polymers were studied intensively by several Russian researchers in the early 1970s. These studies are detailed by Maksimov and Urzhumstev [35]. The interest in environmental effects on composites progressed due to new applications where moisture exposure and strict design compliances must be fulfilled. Offshore oil industry, naval submersibles and automotive industry are few examples of new applications.
Structural composites usually polymeric composites have a natural tendency to absorb water as they have hydroxyl (OH) groups in their molecular structure, which attract water molecules and form hydrogen bonds [36,37]. The ingress of moisture into composites occur by diffusion, which is the transportation of matter by random molecular motion [33]. Diffusion is a concentration gradient based process and removes the chemical potential differences in composites towards a state of equilibrium [38].
A polymer resin consists of occupied volume and free volume [39]. Free volume may be defined as the difference between the volumes at a given temperature at 0°K. The free volume exists in a polymer due to gaps between the polymer chains and depends on the density and physical state of the polymer. The diffusion of water in polymer depends on the available free volume within the polymer as a higher free volume results in a higher capacity for the absorption of water. It allows for higher moisture ingress in polymers by diffusion as it provides passages for diffusing particles [40].
Factors Influencing Moisture Diffusion
Moisture diffusion in polymeric composites have influenced by many factors, such as; temperature, relative humidity, mechanical stress and strain and role of interfaces. The effect of these factors can be seen in the values of diffusion constant and standard moisture content, which can vary remarkably.
Increase in temperature during moisture conditioning results in an increase in the rate of diffusion, as diffusion is a thermally activated process. The temperature dependence of water uptake in polymeric composites/epoxies at different temperature has been studied. Results showed accelerated ageing in the samples that were subjected to humid environment at high temperature. The diffusion coefficients measured from the experimental data showed an increase when the conditioning temperature was increased (Figure 1).
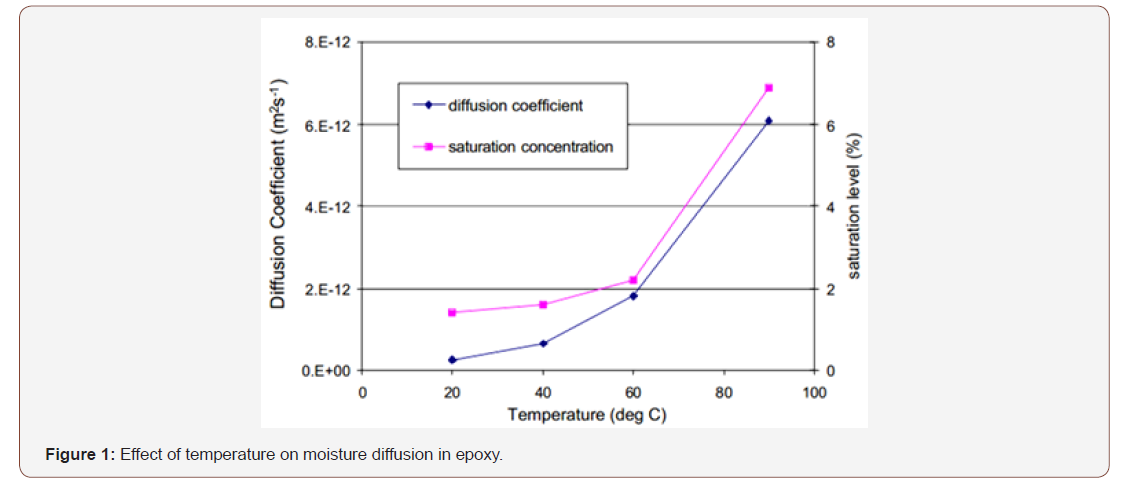
Increase in temperature can also results in an increase in the saturated moisture content. The mobility of molecular chains increases with an increase in temperature, resulting in reduced density owing to thermal expansion. This increases the free volume of the polymer, thus increasing the saturated moisture content [23].
During service many polymers will experience both stress and chemical exposure. Generally mass uptake was carried out free of external stress, although there may be unqualified internal, residual stress, arising from processing, present in materials. The effect of molecular solubility and mobility will depend on the type of stress applied. Hydrostatic tensile stress is expected to increase free volume and open internal voids or crazes, providing additional sites into which molecules can absorb. Conversely, hydrostatic compressive stress will reduce solubility by closing internal sites.
Boersma et al. [26] studied the effects of tensile stress applied to plastic films on their oxygen permeation properties and reported an increase in permeation rate with stress, as shown in Figure 2.
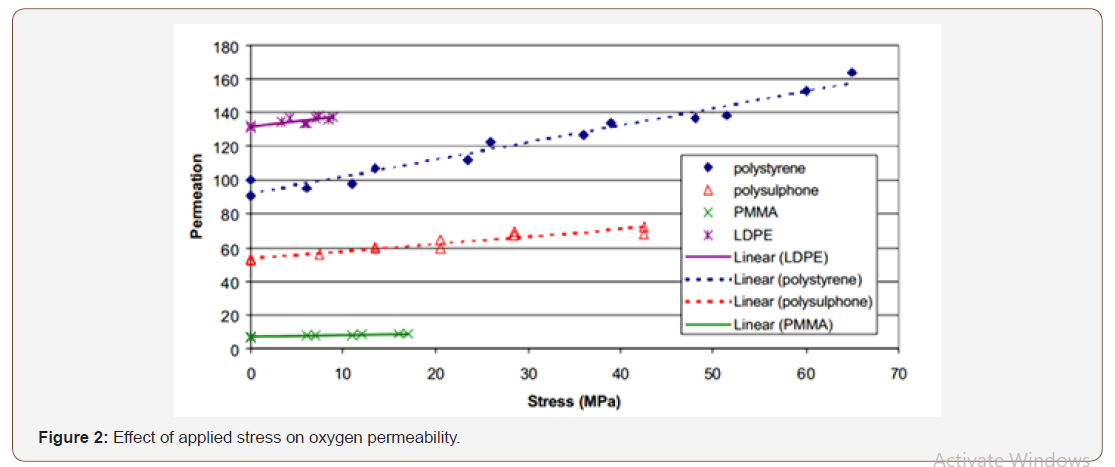
Combined stress and chemical exposure are known to lead to enhanced degradation of polymers and polymer structures. The combination of stress and chemical exposure is known to degrade mechanical performance of adhesive joints far more rapidly than either factor independently.
As permeation through a polymeric material can be described using functions that represent the solubility and diffusion coefficient. Many polymers may not exhibit ideal behaviour, but non-linear functions can be used to represent non-Fickian behaviour. Similarly, most polymers used are filled and can be multi-phase systems with many internal interfaces at micro scale. Materials systems containing macro-scale interfaces cannot usually be treated as a single ensemble material as the size, scale and geometry of the different materials will have an effect whether the interfaces have diffusion properties. System that have macro-scale interfaces include:
Adhesive joints
Laminates
Coating
Multi-layers films
Long-fiber composites
Woven fabric composites
Where macroscopic interfaces occur, the analysis is less straightforward but amenable to analysis if the interfaces play no role in the process. Figure 3 shows schematically the likely difference between diffusion in a multi-layer with interfaces through the thickness, case (i), and parallel to the layers, case (ii).
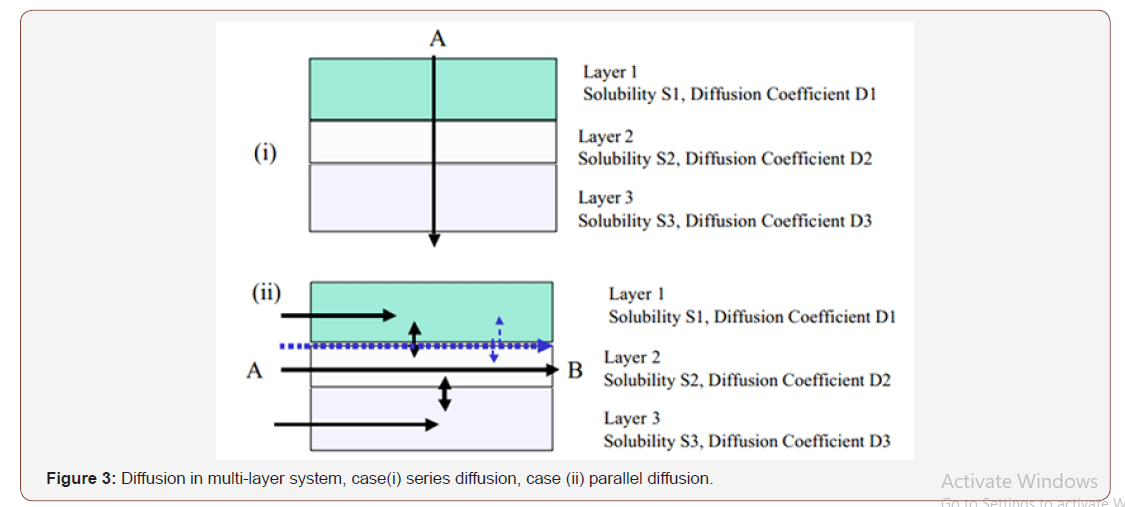
Theory of Diffusion
Moisture diffusion in composites was first theorized by Adolf Fick in 1855 [28] based on the experiments of T. Graham. He also drew considerable inspiration from the analytical theory of heat conduction presented by J. Fourier. Diffusion is the phenomenon governing the transport of material just as conduction is the mechanism of heat transfer. In the case of molecular diffusion, molecules are transported from a higher concentration region to one of lower concentration, it is a spontaneous phenomenon. Mathematically the rate of transfer of diffusion substance through a unit area of a section is proportional to the centration gradient, as given by equation (Figure 4)

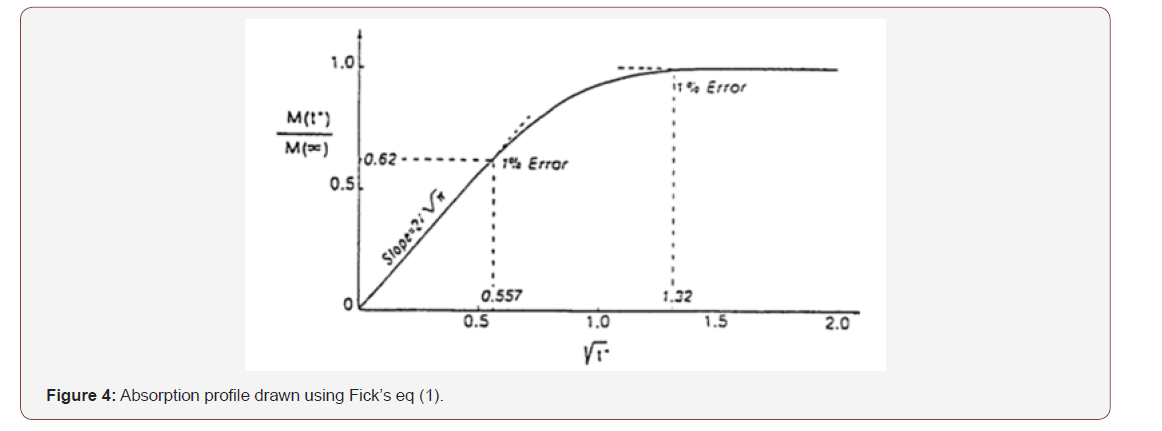
where F is the diffusion flux, D is the diffusion coefficient, C is the concentration of diffusing substance and x is the spatial coordinate. The negative sign is indicating that diffusion is occurring in the opposite direction to increasing concentration.
Moisture uptake in composites has been measured by using several methods. The most commonly methods are based on gravimetric measurements in which change in mass of samples subjected to moist conditions at a given temperature are measure.
ASTM D 570 and ISO 62 are standards that outline measurement methods for water absorption by immersion. Standard sized samples should be dried to constant mass. After immersion for the fixed period, the samples removed from the medium and surface water wiped out. The balance is used to measure absorbed water.
The absorption of many chemicals will reduce the glass transition temperature Tg of polymers. Tg of thermoset polymers such as epoxies are known to vary with moisture content. Tg can be measured using either Dynamic mechanical thermal analysis (DMTA) or differential scanning calorimetric (DSC) measurements. Each specimen had been immersed in deionized water at elevated temperatures (i.e., 25° C, 40° C or 60° C) for a selected period (either 1,2,3 or 6 weeks).
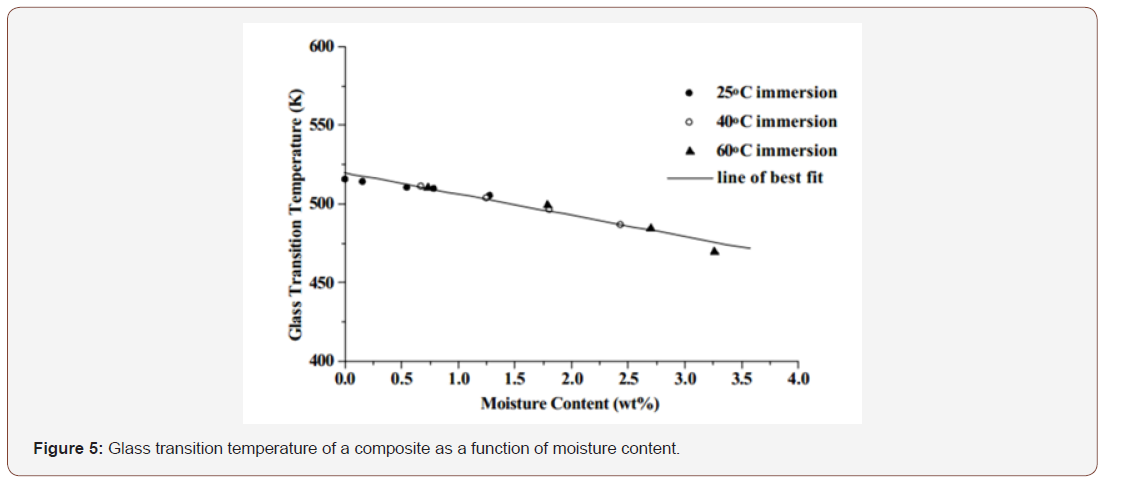
The results in Figure 5 showed that moisture reduces Tg with the shift in temperature being related to moisture content and independent of exposure temperatures. The moisture uptake Tg shift can be represented by the following linear relationship;

where Tgd is the glass transition temperature of the dry material, Tgw is the glass transition temperature of the conditioned (wet) material, g is the temperature shift (in K) per unit moisture absorbed and M is the amount of moisture absorbed (wt.%) (Figure 5).
Tg measurement requires that samples be removed for testing, which makes this measurement a destructive test. DSC measurement require less materials, in mg, and are therefore less invasive than DTMA samples, but such small samples may not be truly representative of the whole component. Development in Nano indentation measurement capabilities offer the possibility of carrying out Tg measurements in-situ, but these techniques will be limited to near surface regions, in common with sampling for DSC or DMTA.
The change in optical properties of a polymer with concentration of absorbing molecules may be used to quantify the concentration provided that suitable calibration curves are available. Beer’s law stating that optical absorption is proportional to concentration of absorbing species may apply if the primary absorption bands of the diffusing species and the polymer are sufficiently separate. Optical transmission properties depend on the plastic being transparent to the optical wavelength selected.
Reflection spectroscopy methods can be used to study the chemical composition of the surface of opaque materials and may be used in combination with sample sectioning to determine through-thickness distribution.
Modelling moisture diffusion
According to Crank [33] “diffusion is the process by which matter is transported from one part of a system to another as a result of random molecular motion”. In organic solids in general, an in polymeric materials in particulars, this process is governed by concentration gradient (Fickian diffusion) and by the chemical potential gradient [7] The former driving force is the prime responsible of the diffusion process when no interaction between the diffusant and the medium is established. Conversely, as generally happens in polymers, a pronounced interaction of the penetrant with the polymer intra and inter-chain bonds generates the necessity of introducing the chemical potential in order to describe correctly the diffusion mechanism. However, in the current practice, the use of this latter more refined method of describing the diffusion process is left aside if the deviation from the Fickian diffusion is small.
Many chemicals will affect the thermo-mechanical properties of the polymer matrix in which they are absorbed. Examples of this include swelling, plasticization (leading to loss of stiffness and strength) and reduction in glass transition temperature in many polymers with the ingress of water/moisture. Monitoring these property changes will provide information on chemical concentrations that could be used to investigate diffusion
It was noted that in many circumstances weight gain data for absorption and desorption of fluids in polymers do not occur with the prediction of linear Fickian diffusion shown in Figure 4. Three types of anomalous weight-gain data in polymers are shown by curves A, B and S as drawn in Figure 6. Some of the anomalies can be attributed to the inherent time- dependent response of polymers. On the other hand, moisture weight gain data in polymeric composites exhibit departure from linear Fickian behavior along curves A, B and S as well as curves C and D as shown in Figure 6. The deviations along curves C and D correspond to severe circumstances and are usually associated with irreversible damage and degradation (Figure 6).
Curve A in Figure 6, denoted as ‘Pseudo-Fickian’, corresponds to the often-encountered circumstance of a continuous gradual increase in weight-gain never attaining equilibrium. Curve B in Figure 6 represented the so-called ‘Two-stage Diffusion’ behavior, while curve S is sometimes associated with a moving diffusion front. However, curve C corresponds to a rapidly increasing moisture content within the composite, which is usually accompanied by large deformation, damage growth, material breakdown or mechanical failure.
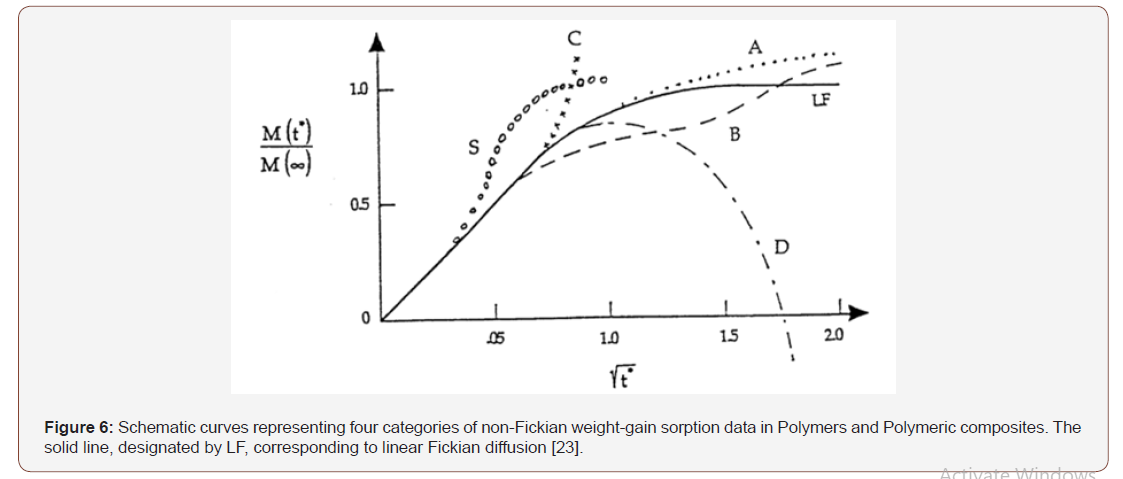
Curve D in Figure 6 represents weight-loss that is attributable to irreversible chemical or physical break-down of material. Generally, weight losses occur in conjunction with hydrolysis, or the separation of side groups from the polymeric chains, or the dissociation of matter located at the vicinities of fiber/matrix interfaces.
Polymeric composites exhibit non-Fickian diffusion as shown by curves A, B and S, in Figure 6. The fact that glassy polymers, with their highly complex molecular configuration, exist in a non-equilibrium thermo-dynamic state accounts for their inherent time-dependent behavior. The above time-dependence is compounded by additional temporal phenomena such as ageing , ongoing chemical reactions [35] and advancing cure. The time-dependence is accelerated by the fact the liquids tend to increase free volume of polymer, thereby lowering their glass transition temperature. Typically, by 10° C for each 1% fluid weight gained in the polymer. The increased mobility of the molecular chains and side-group is denoted as ‘plasticization’. This is essentially reversible phenomenon that can be accounted by means of the time-dependent diffusion model.
Characterization of composite materials
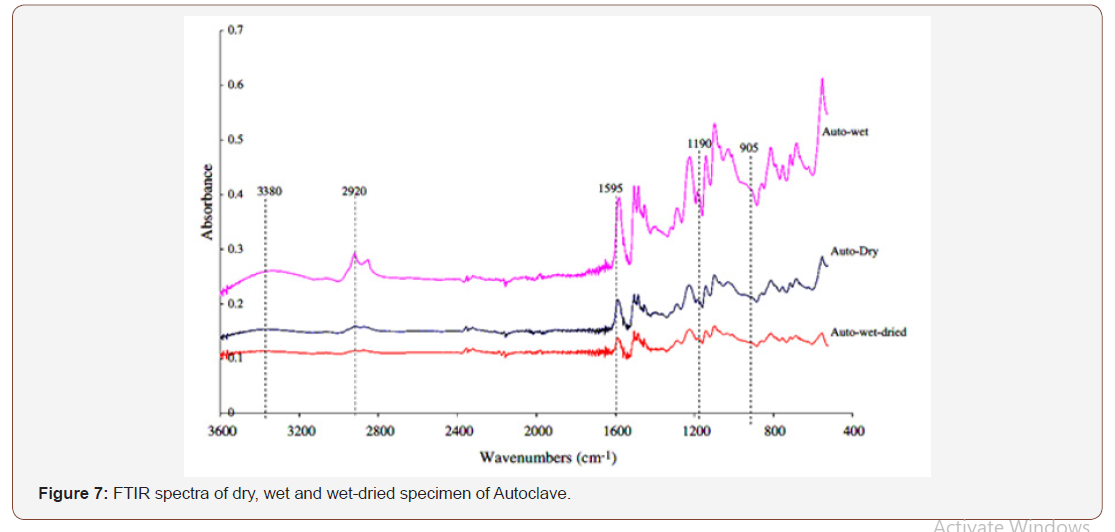
Fourier Transformed Infrared spectroscopy (FTIR) was used to understand moisture diffusion mechanism in composite materials. The spectral information allowed both qualitative and quantitative analysis of moisture absorption mechanism. The chemical function involved in the water sorption phenomenon was identified. The pronounced hydrophilic behavior due to their structure leads to high level of moisture absorption in wet environment (Figure 7).
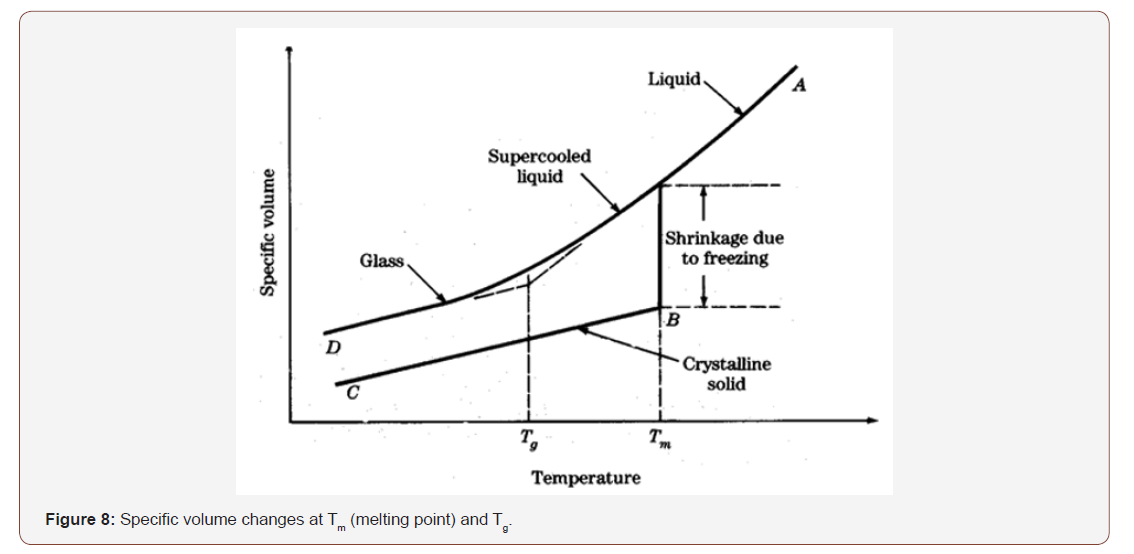
Usually, one of the most significant factors controlling the water diffusion phenomenon in polymeric materials is the molecular interaction occurring between diffusing compound and the substrate. The diffusion phenomenon is subjected to the ability of the polymer molecular to establish hydrogen bond with the water molecules. The glass transition temperature Tg is a very important parameter of epoxy resin matrix composites because Tg establishes the service environment for the materials’ usage. In most applications, the epoxy is used at a temperature well below Tg (i.e., in the glassy state). Usually, when the material is exposed in hydrothermal environment Tg decrease and therefore the service temperature of the materials changes. This modification in Tg reveals the degree of plasticization and water/resin interactions arising in the material (Figure 8).
Reported data of Tg in the technical literature exhibit a rather wide scatter band for a given epoxy system. Usually, the variation in Tg is explained by difference associated with material preparation. The effect of hydrothermal history, i.e., exposure time and temperature on Tg is certainly exhibited.
The composite shear properties are primarily influenced by matrix and fiber/matrix interface. Dry specimens have higher Inter laminar shear strength (ILSS) vales than wet specimens distressing by the same ageing, which is due to physical changes inside, e.g. matrix plasticization. It is observed that ILSS has lower values at higher temperature than at lower temperature. Factors responsible for this phenomenon are plastic deformation at higher temperature, and internal stress change (rise) at fiber/matrix interface due to different coefficient of thermal expansion resulting in interfacial deboning. Various models are available to correlate temperature dependence with strength of composites.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Bao L, Yee AF (2002) Moisture diffusion and hydrothermal aging in bismaleimide matrix carbon fiber composites - part I : uni-weave composites. Compos Sci Technol 62(16): 2099-2110.
- Zhou J, Lucas JP (1999) Hydrothermal effects of epoxy resin . Part I : the nature of water in epoxy. Polymer 40: 5505-5512.
- Leger R, Roy A, Grandidie JC (2013) A study of the impact of humid aging on the strength of industrial adhesive joints. Int J Adhes Adhes 44: 66-77.
- Costa ML, Almeida SFM de, Rezende MC (2005) Hydrothermal effects on dynamic mechanical analysis and fracture behavior of polymeric composites. Mater Res 8(3): 335-340.
- Shen CH, Springer GS (1977) Effects of Moisture and Temperature on the Tensile Strength of Composite Materials. J Compos Mater 11(1): 2-16.
- Gautier L, Mortaigne B, Bellenger V (1999) Interface damage study of hydrothermally aged glass- fibre-reinforced polyester composites. Compos Sci Technol 59(16): 2329-2337.
- Naceri A (2009) Modeling of the Mechanical Behavior of Composite at Different Relative Humidities. Strength of Materials 41(4): 444-448.
- Verpoest I, Springer GS (1988) Moisture absorption characteristics of aramid-epoxy composites. J Reinf Plast Compos 7(1): 2-22.
- Vieth WR, Sladek KJ (1965) A model for diffusion in a glassy polymer. J Colloid Sci 20(9): 1014-1033.
- Tsenoglou CJ, Pavlidou S, Papaspyrides CD (2006) Evaluation of interfacial relaxation due to water absorption in fiber–polymer composites. Compos Sci Technol 66(15): 2855-2864.
- Sih GC, Shih MT, Chou SC (1980) Transient hydrothermal stresses in composites: coupling of moisture and heat with temperature varying diffusivity. Int J Eng Sci 18: 19-42.
- Tsui CP, Tang CY, Fan JP, Xie XL (2004) Prediction for initiation of debonding damage and tensile stress – strain relation of glass-bead-filled modified polyphenylene oxide. Int J Mech Sci 46(11): 1659-1674.
- Li Y, Miranda J, Sue H (2001) Hydrothermal diffusion behavior in bismaleimide resin. Polymer 42(18): 7791-7799.
- Vogt BD, Soles CL, Jones RL, Wang C, Lin EK, et al. (2004) Interfacial Effects on Moisture Absorption in Thin Polymer Films. Langmuir 20(13): 5285-5290.
- Zafar A, Bertocco F, Schjødt Thomsen J, Rauhe JC (2012) Investigation of the long term effects of moisture on carbon fibre and epoxy matrix composites. Compos Sci Technol 72(6): 656-666.
- Leali M, Frascino S, Almeida M De, Cerqueira M (2005) Hydrothermal Effects on Dynamic Mechanical Analysis and Fracture Behavior of Polymeric Composites. Mater Res 8(3): 335-340.
- Chiou P, Bradley WL (1995) Effects of seawater absorption on fatigue crack development in carbon/epoxy EDT specimens. Composites 26(12): 869-876.
- Jedidi J, Jacquemin F, Vautrin A(2006) Accelerated hydrothermal cyclical tests for carbon/epoxy laminates. Compos Part A Appl Sci Manuf 37(4): 636-645.
- Chandrasekaran VCS, Advani SG, Santare MH (2011) Influence of resin properties on interlaminar shear strength of glass/epoxy/MWNT hybrid composites. Compos Part A Appl Sci Manuf 42(8): 1007-1016.
- Weitsman YJ, Elahi M (2000) Effects of Fluids on the Deformation, Strength and Durability of Polymeric Composites- An Overview. Mech Time Dependent Mater 4(2): 107-126.
- Gigliotti M, Jacquemin F (2013) On cyclical hydrothermal fields in laminated plates. J Compos Mater 47: 231-242.
- Weitsman YJ(1995) Effects of Fluids on Polymeric Composites - A Review. Contract Technical Report - The University of Tennessee, Knoxville, TN, USA.
- Duncan B, Urquhart J, Roberts S (2005) Review of Measurement and Modelling of Permeation and Diffusion in Polymers. National Physical Laboratory, Middlesex, UK.
- Olmos D, Gonzalez-Benito J (2010) Composites formed by glass fibers and PS-modified epoxy matrix. Influence of the glass fibers surface on the morphologies and mechanical properties of the interphases generated. Polym Compos 31(6): 946-955.
- Damson MJ (1980) Thermal expansion and swelling of cured epoxy resin used in graphite/epoxy composite materials. J Mater Sci 15(7): 1736-1745.
- Boersma A, Cangialosi D, Picken SJ (2003) Mobility and solubility of antioxidants and oxygen in glassy polymers III. Influence of deformation and orientation on oxygen permeability. Polymer 44(8): 2463-2471.
- Vrentas JS, Vrentas CM (2003) Diffusion in glassy polymers. J Polym Sci Part B Polym Phys 41(8): 785-788.
- Fick A (1855) Ueber diffusion. Ann Phys 170(1): 59-86.
- Rogers CE (1965) Solubility and diffusivity. Wiley: New York.
- Comyn J (Edt) (1985) Polymer Permeability. Springer Netherlands, Dordrecht, Netherland.
- Frisch HL (1970) “Diffusion in polymers” edited by J Crank and GS Park, Academic Press, London and New York, 1968; 452 pg. J Appl Polym Sci 14(6): 1657-1657.
- Stannett V, Hopfenberg HB, Petropoulos JH (1972) Diffusion In Polymers. Diffus Polym.
- Crank J (1979) The Mathematics of Diffusion. Oxford University Press, UK.
- Ghez R (1988) A Primer of Diffusion Problems. John Wiley & Sons, USA.
- Maksimov RD, Urzhumstev YS (1977) Prediction of the LongTerm Durability of Polymer Materials. A Review Mekh Polim 4: 631-645.
- Olmos D, Gonzalez‐Benito J (2010) Composites Formed by Glass Fibers and PS-Modified Epoxy Matrix . Influence of the Glass Fibers Surface on the Morphologies and Mechanical Properties of the Interphases Generated. Polym Compos 31(6): 946-955.
- Deng S, Ma W, Zhou X, Fan C (2013) Maintenance of highly interfacial shear strength by diblock copolymer between carbon fiber and epoxy resin in hostile environment. Compos Interfaces 19(8): 499-509.
- Alfrey T, Gurnee EF, Lloyd WG (1966) Diffusion in glassy polymers. J Polym Sci Part C Polym Symp 12(1): 249-261.
- Prolongo SG, Gude MR, Ureña A (2012) Water uptake of epoxy composites reinforced with carbon nanofillers. Compos Part A Appl Sci Manuf 43(12): 2169-2175.
- Kumosa L, Benedikt B, Armentrout D, Kumosa M (2004) Moisture absorption properties of unidirectional glass / polymer composites used in composite ( non-ceramic ) insulators. Compos Part A 35(9): 1049-1063.
-
Farkhanda Afza, Rukhsana Bibi, Deeba Afzal, Faryal Chaudry. Hydrothermal Ageing Impact & Damage Characterization for Polymeric Composites by means of Experimental Techniques. Mod Concept Material Sci. 2(2): 2019. MCMS.MS.ID.000533.
-
Hydrothermal ageing, Moisture diffusion, Fiber fracture, Fiber-matrix deboning, Unidirectional composites, Polymeric composites
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






