Dislocation-Monovalent Cations Interaction in Sodium Halide Crystals During Plastic Deformation

Combination method of strain-rate cycling tests and ultrasonic oscillation has been considered to give the information on the dislocation motion on the slip plane containing many weak obstacles (e.g., impurity atoms, isolated and clustered point defects) and a few strong ones (forest dislocations) in bulk during plastic deformation at low temperature (e.g., [1]). When the ultrasonic oscillatory stress is applied to a plastic deforming crystal, the applied stress drop is appeared on a stress-strain curve. The decrease of applied stress increases with stress amplitude at a given temperature and shear strain [1]. The strain-rate sensitivity of flow stress, which is inversely proportional to the average length of dislocation segments [2], was measured here on the basis of stress change due to the strain-rate cycling in the middle of ultrasonic oscillatory stress. By using the above-mentioned method, the influence of anion size of host crystal on the mechanical properties is investigated at low temperature for sodium halide crystals doped with monovalent cations (NaCl:Li+ and NaBr:Li+) in this paper.

NaCl single crystals doped with Li+ ions were prepared by cleaving to the size of 5×5×15 mm3 as the specimens used in this study. The concentration of dopant ions was 0.5 mol% in melt. The specimens were annealed at 973 K for 20 h and were gradually cooled to room temperature at 40 Kh^-1 for the purpose of reducing dislocation density as much as possible.

The strain-rate cycling tests combined with ultrasonic oscillation (20 kHz) were conducted keeping the stress amplitude (τ_v) constant during plastic deformation for the specimens at 77 to 253 K. Application or removal of ultrasonic oscillation causes the stress drop (Δ_τ) and strain-rate cycling between ε̇1(1.1×10^-5s^-1) and ε̇₂ (5.5×10^-5 s^-1) makes the stress change (Δτ’) during the tests. The strain-rate sensitivity (λ) of flow stress was derived from Δτ’ value (i.e., λ=Δτ’/Δlnε̇=Δτ’/1.609). This was detailed in the previous paper [3].

The variation of Δ_τ with shear strain is shown in Figure 1 for NaCl:Li+ (0.5 mol%) at 143 K. The numbers besides each symbol in the figure represent the output voltage from the piezoelectric transducer set on the bottom of specimen, which is proportional to τ_v. Δ_τ values do not largely change at all stress amplitudes and are almost constant, irrespective of strain. Δ_τ also tends to be larger with τ_v at a given temperature and strain. While the variation of λ of flow stress with it is shown in Figure 2 for the same specimen. λ values tend to increase with strain above about 5% and decrease with τ_v at a given temperature and strain. Δλ/Δτ_v is small at a given strain for low and high τ_v regions, as seen in Figure 2.

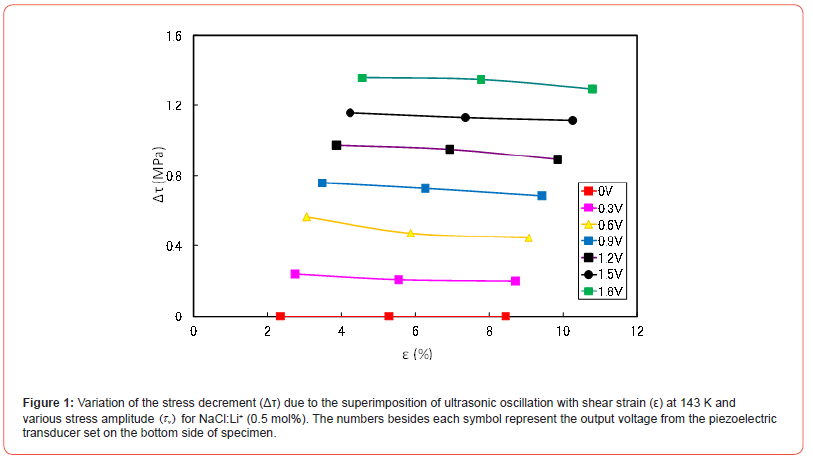
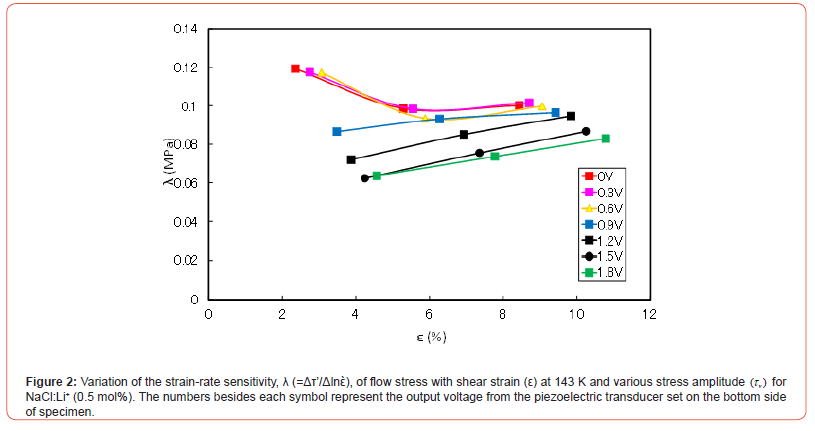
The relations between Δτ and λ for each output voltage in Figures 1 and 2 are plotted for the specimens at strains of 5 and 8% and 143 K in Figure 3. The Δτ versus λ curves have stair-like shape: two bending points and two plateau places. That is to say, the first plateau place ranges until first bending point and second one extends from the second bending point. λ decreases with Δτ between the two bending points.

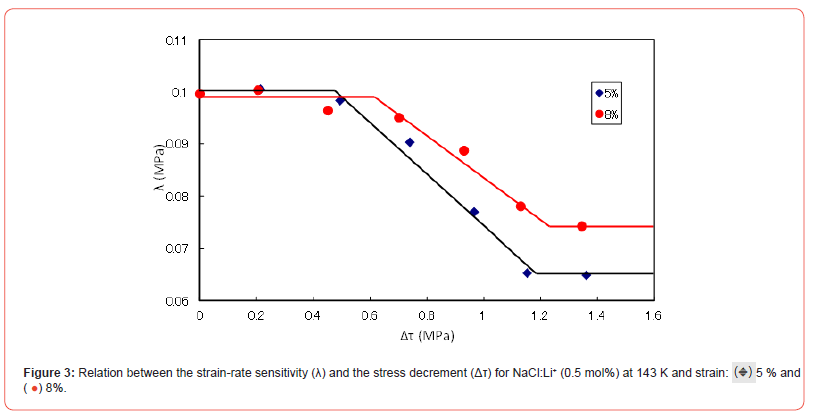
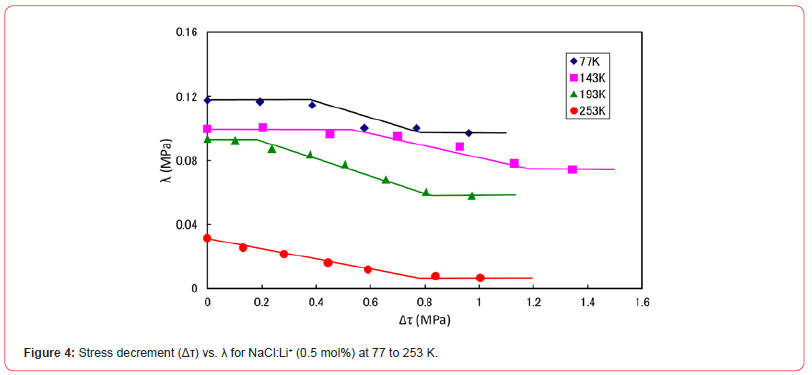
Figure 4 shows the Δ_τ versus λ curves for NaCl:Li⁺ (0.5 mol%) at various temperatures. The numbers besides each symbol in the figure represent the temperature of the specimens. The curves also have stair-like shape at low temperatures (i.e., 77 and 193 K), but the first plateau place cannot be seen at 253 K, as can be seen in Figure 4. Similar variation of Δ_τ versus λ curve with temperature has been observed for NaBr:Li⁺ (0.5 mol%) single crystals at 77 to 263 K [4]. Figure 5 concerns the relative curves for NaBr:Li⁺. The length of Δ_τ within first plateau place is referred as τ_p in Figure 5. It seems from Figures 4 and 5 that τ_p tends to be lower at higher temperature for the two kinds of specimens: NaCl and NaBr crystals doped with Li⁺ ions. When a dislocation moves overcoming the short-range obstacles such as dopant ions with thermal activation during plastic deformation, it is considered that τ_p is the effective stress due to the dopants, because τ_p depends on the type and the density of obstacles (e.g., [5, 6]). Therefore, observation of τ_p will provide information on dislocation-monovalent cations interaction in the specimens. Namely, τ_p versus temperature relation reflects the dislocation-monovalent cations interaction in a crystal.

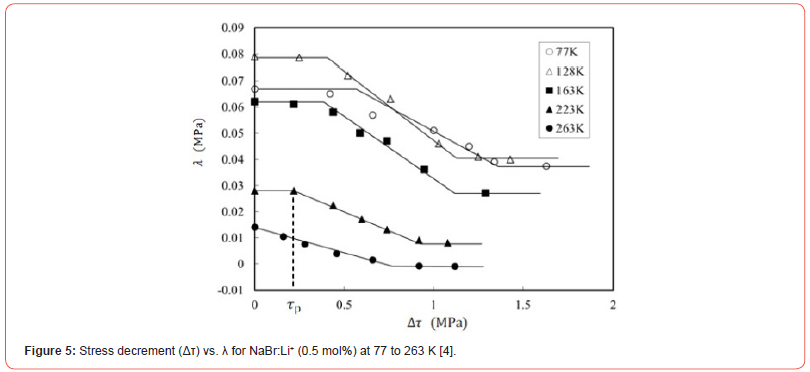
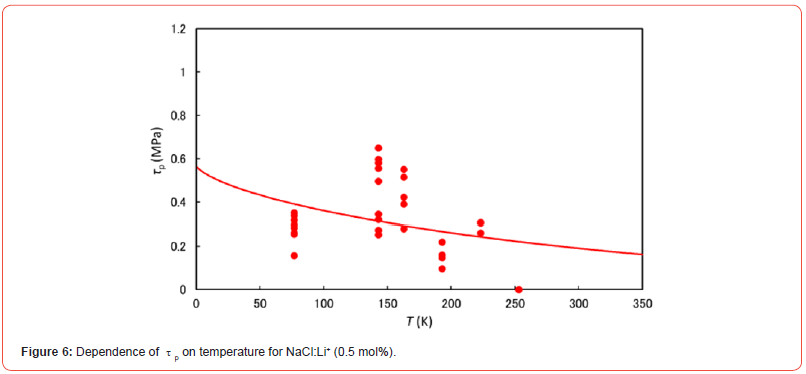
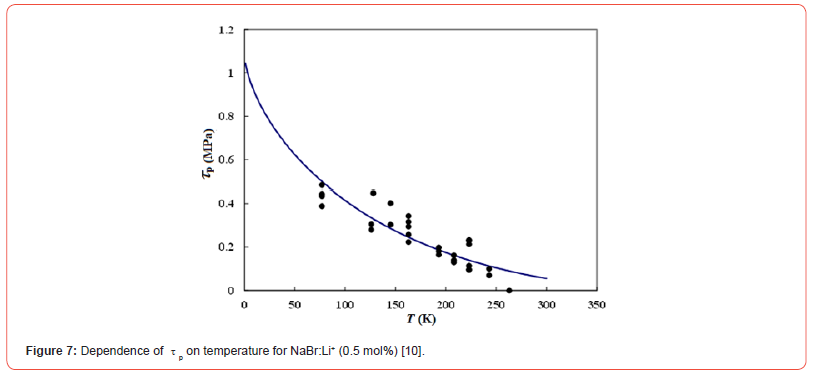
Isotropic defects (Δ_ε) occur around Li+ ions in NaCl:Li+ or NaBr:- Li+ crystals, since the dopant ionic size is different from the substitutional ions (Na⁺) of the host crystal. Then, the force-distance profile between a dislocation and the symmetry defect is expressed by the Cottrell and Bilby relation [7] taking account of the Friedel relation [8]. The plots in Figures 6 and 7 represent τ_p values for NaCl:Li⁺ and NaBr:Li⁺ crystals at 77 to 263 K and are approximated by the Cottrell and Bilby relation, where the solid curves in these figures were obtained by numerical calculation with the parameters (τ_p0, T_c, and G₀) as to be fitted to the solid circles using the least-squares method. These parameters are denoted in Table 1. τ_p0 is the τ_p value at the temperature of 0 K. T_c is the critical temperature at which τ_p is zero and does not depend on the concentration of dopant ions [9]. τ_p value decreases with increasing temperature and approaches to zero at the critical temperature (T_c) as seen in Figures 6 and 7. Tc for NaCl:Li⁺ crystal is near the melting point and is much higher than T_c (469 K) for NaBr:Li+ [10, 11]. G₀ is the activation energy for the breakaway of a dislocation from the isotropic defect around dopant (i.e., Li⁺ ion here) in the absence of an applied stress.

Table 1:Parameters used for calculation.

Table 2:Values of the lattice constants at room temperature (298 K) and atmospheric pressure, and defect size (Δε) for each specimen.

The values of Δε are given in Table 2 for each specimen. These values are calculated from the difference between the lattice constants of host crystal and dopant one. The lattice constants are also given in the table. As a result, the Δ_ε is 0.089 for NaCl:Li⁺ crystal and is 0.079 for NaBr:Li⁺. As the anion size of host crystal is slightly small, the isotropic defect around Li+ ion is somewhat large. This leads to the difference in activation energy between the two kinds of crystals (G₀=0.55eV for NaCl:Li⁺ [11], G₀=0.50eV for NaBr:Li⁺ [10]) for overcoming the isotropic defect by a dislocation.

Δτ versus λ curves, which were obtained by the strain-rate cycling tests combined with ultrasonic oscillation, have stair-like shape for NaCl:Li⁺ (0.5 mol%) single crystal at low temperature. Observation of Δ_τ at the first bending point on the curve, i.e. τ_p, gives us useful information on moving dislocation during plastic deformation. Assuming that the temperature dependence of τ_p is approximated to the Cottrell-Bilby relation taking account of the Friedel relation, the activation energy is 0.55 eV for overcoming the isotropic defect around the dopant (Li⁺) in NaCl:Li⁺ crystal by a dislocation. As the anion size of host crystal is small, its value becomes somewhat large in contrast to 0.50 eV for NaBr:Li⁺, since the isotropic defect around Li⁺ ion becomes slightly large in the crystal (i.e., Δ_ε varies from 0.079 for NaBr:Li⁺ to 0.089 for NaCl:Li⁺).

Dr. T. Ohgaku, as well as S. Yamaguchi are acknowledged for his collaboration in the analysis on Δτ and λ data, as well as for his experimental assistance.

No conflict of interest.

1. Kohzuki Y (2018) Study on dislocation-dopant ions interaction in ionic crystals by the strain-rate cycling test during the Blaha effect. Crystals 8(1): 31-54.
2. Conrad H (1964) Thermally activated deformation of metals. Journal of Metals 16: 582-588.
3. Kohzuki Y (2023) Study on X-ray-Induced defects as barriers for dislocation motion by strain-rate cycling tests combined with ultrasonic oscillation. Modern Concepts in Materials Science 5(2).
4. Kohzuki Y, Ohgaku T (2017) Study on influence of additive and host ions on deformation characteristics of alkali halide crystals by strain-rate cycling tests during the Blaha effect. Crystal Research and Technology 52(3): 1600290.
5. Ohgaku T, Matsunaga T (2009) Interaction between dislocation and divalent impurity in KBr single crystals. IOP Conference Series: Materials Science and Engineering 3(1): 012021.
6. Ohgaku T, Teraji H (2001) Investigation of interaction between a dislocation and a Br^– ion in NaCl:Br^– single crystals. Status Solidi A 187(2): 407-413.
7. Cottrell AH, Bilby BA (1949) Dislocation theory of yielding and strain ageing of iron. Proceedings of the Physical Society of London A 62: 49-62.
8. Friedel J (1964) Dislocations. Pergamon Press, Oxford pp. 223-226.
9. Ohgaku T, Takeuchi N (1992) Interaction between a dislocation and monovalent impurities in KCl single crystals. Phys. Status Solidi A 134(2): 397-404.
10. Kohzuki Y (2022) Study on thermal activation barrier for dislocation motion by strain-rate cycling tests combined with ultrasonic oscillations. Modern Concepts in Materials Science 5(1).
11. Kohzuki Y, Ohgaku T (2016) Activation energy for dislocation breakaway from various monovalent ions in NaCl single crystals. Philosophical Magazine 96(29): 3109-3119.
12. Sirdeshmukh DB, Sirdeshmukh L, Subhadra KG (2001) Alkali halides. Hull R, Osgood RM, Sakaki Jr.H, Zunger A, eds., Springer-Verlag, Berlin Heidelberg p. 6.