A Review on Auxetic Textile Structures, Their Mechanism and Properties

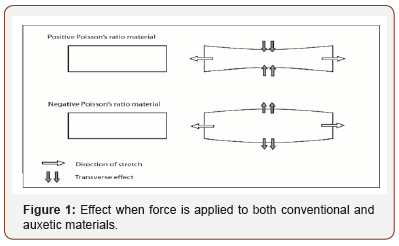
Almost all materials possess a positive Poisson’s ratio, in the sense that they shrink when stretched and expand when compress. These are basically referred to as conventional materials and their Poisson’s ratio (v) value ranges from 0.0 to 0.5 [1]. Unlike the conventional, auxetic materials exhibit a negative Poisson’s ratio (NPR), which laterally expand when stretched and laterally contract when compressed [2]. Knowledge about auxetics can be trace as far back in the 1800s where Voigt et.al had already discovered the NPR in some materials but didn’t draw much attention to it [3]. Later in 1987 a man by name Lakes reported an auxetic foam structure that could be produced easily by tri-compression and heating which were considered to be a man-made process [4]. Developments on auxetic materials thereafter have never ceased. Scientist and researchers have comprehensively, dived into knowing every bit about auxetics, right from its structure and deformational behavior as compared to conventional materials, to how it could be artificially produced and its application thereafter. Figure 1 shows the effect that occurs when a force is applied to both conventional and auxetic material.

Poisson’s ratio basically describes the relative change in the natural dimension of an object when a load is applied in a longitudinal direction or other way [5]. Mathematically, it could be expressed as;

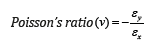
Where ε^y and ε^x are transverse strain and axial strain respectively.

Auxetic mechanical metamaterials according to [6] are engineered systems that exhibit the unusual macroscopic property of a negative Poisson’s ratio due to sub-unit structure rather than chemical composition. The auxetic of a material is dependent on its geometrical structure and the material’s system and deformation mechanism when a load is applied [7]. Most engineering materials have a higher shear modulus G than their bulk modulus K, and by changing the microstructure of a material in such a way that the Poisson’s ratio (v) is lower, the values of K and G can be altered if the Young’s modulus(E) is kept constant [8]. Auxetic materials are described to be counterintuitive, and it is to this property that much interest has been drawn to the development of auxetics. Again, the various beneficial effects attached to NPR materials such as the enhancement of shear stiffness, increase in the plane strain fracture toughness, increased indentation resistance, and improvement on the energy absorption properties are all as a result of this counterintuitive property [9].

In fact, in an attempt to attain a better insight into the mechanisms that result in auxetic, various geometry-based models have been proposed and developed not only to explain the observed negative Poisson’s ratios in naturally occurring auxetic materials, but also to act as a blueprint for the design and manufacture of novel man-made auxetics [10]. It is said, that majority of negative Poisson’s ratio materials are cellular solids such as honeycombs and foams. Currently, there are a number of structural designs base on which auxetic materials are being produced. These designs have been proposed, tried and tested, amongst which includes; chiral honeycomb structures [11,12] 2D and 3D reentrant structures [13- 17], angle-ply laminates [18,19], rotational rigid/ semi-rigid units [7,20-23] liquid crystalline [24] and nodule and fibril structure.

Over the past few years, a number of auxetic materials ranging from macrostructure to microstructure have been proposed and fabricated. The mechanism of these materials is basically, expanding in a perpendicular direction when a load is applied to the structure in one direction. (i.e. when the load is applied in the vertical direction, the expansion occurs in the horizontal direction). Below are some auxetic structures with their deformational mechanisms.

Chiral honeycomb model

Chiral honeycomb models are auxetic cellular structures that exhibits negative Poison’s ratio [25]. They are formed by connecting straight ligaments (ribs) to the central nodes, which is either in the form of a circle, a rectangle or any other geometrical shape or form. The individual chiral units are joined together to form a complete chiral structure. When a force is applied to the structure, the ligaments tend to wrap or unwrap around the nodes giving the structure its auxetic effect. The nodes and ligaments of this chiral honeycomb configuration as already mentioned provides substantially decoupled structural functions, with the nodes carrying out essentially the compressive resistance, while ligaments bear the majority of the shear loading [26]. Figure 2 describes a unit cell of a chiral honeycomb structural analysis used by[11] in their work.

The structure is composed of circular nodes/elements with equal radius r and connected by straight ligaments with equal length L. These ligaments are constrained to be tangential to the circular nodes, and the angle between the adjacent ligaments is 60 . Both the nodes and ligaments have a common wall thickness t and depth d. Base on the theoretical and experimental investigations conducted by Prall and Lakes [11], the Poisson’s ratio of a chiral structure for in-plane deformations can be tailored to be around -1. Their analytical basis is summarized in Figure 2.

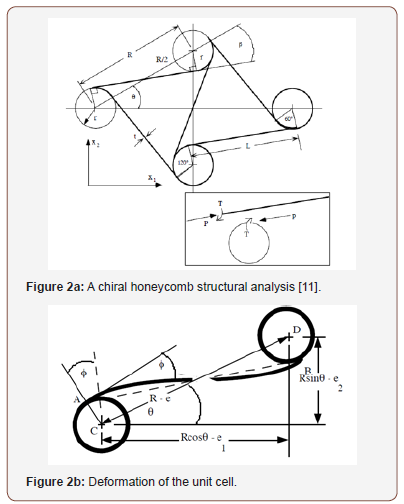
As shown if Figure 2b, the displacement of the node centers results in the orthogonal deformation of the honeycomb. The angular deflectionφ of beam AB measured at its endpoints coincides with the nodes’ rotation through the same angle,φ .This is due to the constraint that the slope of AB, at A or B, remains tangent to the node. So, in order to maintainφ andθ , the ligaments must “wind” onto the nodes [11]. From Figure 2b, the deformation e, of the cell is the same for both nodes C and D and is related to the angular deflectionφ of AB by;

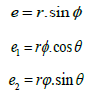
Of which, for small deflection, r sinφ ≈ rφ andθ = 30 . According to [8], by using the elementary beam theory, if the thickness is t, the deflection eventually becomes:

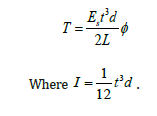
The strains, therefore, become:

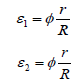
Poisson’s ratios, for loading in both directions can then be calculated as:

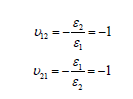
The shape of the nodes and the length of the ligament determines the structure auxetic effect in an experimental observation stated, that with increase in the radius of the cylindrical members (nodes), the effective modulus of the sample decreases, which is attributed to the fact that higher cylindrical members(nodes) makes the ligaments shorter thus reducing the strength of the geometry [25,27]. In addition to achieving a Poisson’s ratio of -1 in an inplane deformation by Prall and Lakes (1997), the Poisson’s ratio was also maintained over a significant range of strain, in the known negative Poisson’s ratio materials [11]. Figure 3 shows the various chiral honeycomb structures available.

Currently the available chiral honeycomb structures as shown in Figure 2 includes; 3-ligaments chiral structure, also kwon as the tri-chiral and anti-tri-chiral honeycomb, 4- ligaments chiral structure, also known as the tetra-chiral and anti-tetra-chiral honeycomb [28,29], 4- ligaments rectangular chiral structure [10], 6- ligaments chiral structure, also known as the hexagonal chiral honeycomb [11,30].

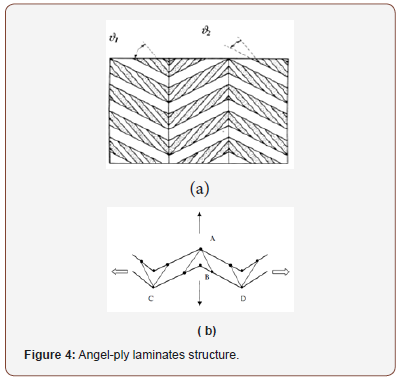
Angle-ply laminates structures

Auxetic angel-ply laminates according to [31,32] has been proposed by G.Milton who designed another method of biphasic composite material which incorporates a stiff inclusion and a compliant matrix.

As indicated in Figure 4(a), the hatched region represents a compliant phase simulated by compliant tensile but flexural rigid rods. The dash line in the figure represents the periodicity cell which is attained by placing in the middle of each rod a sliding element. A pair of rigid rods fastened by two triangular links is used to replace each rod so as to prevent the surface from sliding to each other and also to retain parallelism.

Figure 4b represents a rod model which describes the deformation behavior of such laminates. In this situation under an infinitely small deformation, the expansion that occurs within the width AB is directly proportional to the increase of length CD. A sandwich like stack of such structures could achieve auxetic effect. The white and black arrows indicate the direction of force and shear respectively [32].

Rotation of rigid/ semi rigid units

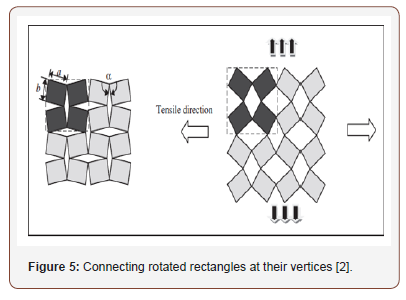
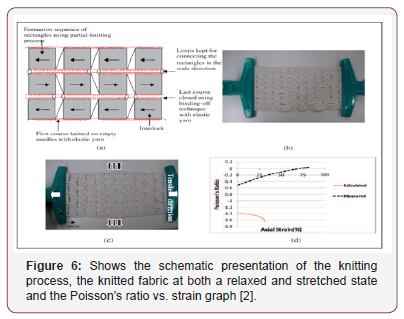
In this form of structure, different/ uniform geometrical shapes such as rigid/semi rigid squares [22] triangles [33], rectangles [7] and tetrahedron [34] are configured at their selected vertices. The auxetic of this structure comes as a result of the rotation of these shapes when stretched at a particular direction. This model was discovered first by Grima and Evans in an inorganic crystalline material. The idea of rotating squares with rigid units was found to be independent to the initial geometry and the loading direction, keeping the NPR at -1 [35]. Further studies were conducted in order to better understand the deformational characteristics of this auxetic structure. An auxetic fabric was constructed by Hu et al. and the fabric construction was based on the arrangement of rigid rectangles connected together at their vertices by hinges. The resultant fabric knitted had only the auxetic effect when stretched at the course direction [2]. Figure 5 shows the arrangements of the rigid rectangles whereas Figure 6 shows the knitted fabric and its corresponding tests.

CNT sheet is being developed around the world to form advanced lightweight materials [3-7]. The material cost is high, and the manufacturing throughput is low. Alternatively, metals have different properties including low cost and high conductivities, while ceramics provide abrasion resistance and fire retardancy. A barrier in materials science has been the inability to manufacture a material that integrates carbon materials and metals or ceramics together to form a reliable material whose properties can be customized to meet specific application requirements. Much research has been focused on developing nanocomposite materials for structural applications or electrical conduction. An alternative application is to produce nanotube hybrid sheet for use as performance fabrics and textiles. Shown here are early results from developing a continuous manufacturing process to integrate NMP with CNT to produce continuous textile material whose properties vary based on the constituent metals. A difference is the CNHT produced here is a nonwoven material whereas most textiles are woven using fibers.

CNHT are formed using a modified floating catalyst gas phase pyrolysis method that produces carbon nanotubes (CNT). Carbon Metals may be formed by joining carbon atoms or CNT with metal/ alloy atoms or clusters of atoms in a high temperature reaction. The metal atoms are supplied as metal NMP in the high temperature nanotube floating catalyst synthesis process. The CNT and metals join chemically or physically to produce a nanotube sock (Figure 1) that is wound on a drum. The CNHT process allows the properties of sheet to be customized to a limited degree based on the NMP used, and the end application goal. Conductivity, strength, porosity, capillarity, flame retardancy, and other properties can be partially tailored based on the NMP material, size, and geometry. A key advance in the process is the rapid integration of the precursor metals at high temperature, the short growth time, and fast cooling of the carbon species. Fast windup of the nanotube sock produces partially aligned tape. The CNT and metals interlock physically or chemically to form a semi-homogeneous material. Many combinations of materials design are possible. CNHT is a new perspective in manufacturing and can provide new materials for engineered systems.

Liquid crystalline polymer model/ structures

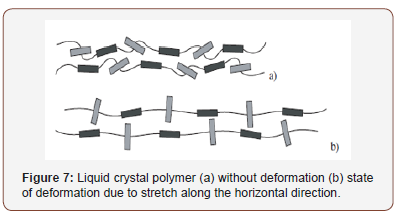
The liquid crystalline polymer (LCP) is composed of chains of rigid rod molecules which are connected by flexible spacer groups along the length of the chain. As already said, this model is divided into two segments, a softer/ flexible segment and a rigid segment. These flexible spacer groups/ segments are connected either terminally or laterally to the end of the rigid rod/ segments [21], and the connection is along the length of the soft segment. The auxetic of this model/ structure is exhibited when there is a lateral rotation of the rigid rod or segment in a perpendicular direction to the horizontal one [36].

Figure 7 shows the model under two states, which is the relaxation state (a) and deformation state (b). It could be seen that the model under relaxation state present the rigid rod as lying horizontally along the direction of the main chain. And under the deformation state where a load/ force is applied, the rigid rod becomes perpendicular to the horizontal direction of the main chain through its rotation, which then result in the increase in the distance between the molecular chain within the LCP. This can be seen as illustrated in Figure 7a&b.

Re-entrant structures

Re-entrant auxetic honeycombs could either be 2D or 3D structures. Their ability to exhibit a negative Poisson’s ratio (NPR) makes them well known and the most commonly used auxetic structure. In “1982” Gibson et al. suggested the first re-entrant honeycomb 2D macroscopic auxetic cellular structure [13]. The deformation which results in the auxetic of these structures occurs by flexure and hinging of the diagonal ribs within the structure, with response to an applied force or load. The rotation of the ribs towards the horizontal direction when the force is applied leads to a transverse expansion of the structure. Figure 8 illustrates a reentrant honeycomb structure.

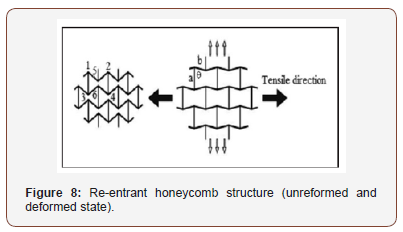
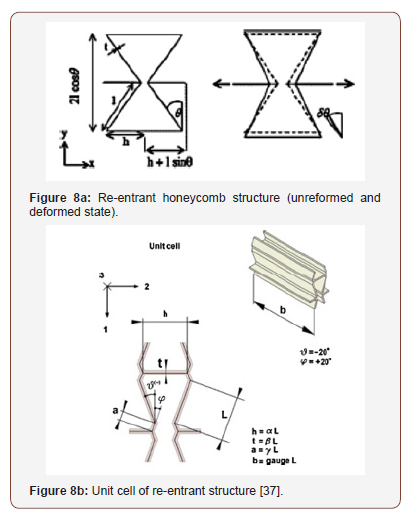
The basic hexagonal unit cell used for mathematical calculation of most re-entrant geometry is shown in Figure 8a&b The Poisson’s ratio and Young’s modulus in the loading direction for this figure are given by;

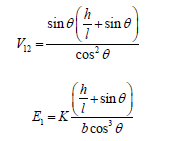
Where h , l ,b , andθ are as defined in Figure 8a, 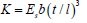and E is the intrinsic Young’s modulus.

Lira et al. evaluated the transverse shear properties of a center symmetric honeycomb structure using analytical and finite element models [37]. Their cellular structure features a unit cell geometry that allows in-plane auxetic deformations, and multiple topologies to design the honeycomb for multifunctional applications. The outof- plane properties were calculated using a theoretical approach based on Voigt and Reuss theories [8] which can be used to perform a parametric analysis for the design of the cores in classical and multifunctional sandwich constructions [38]. Figure 8b shows the unit cell of the re-entrant structure that was evaluated.

The 3D re-entrant honeycomb model was produced to make up for the short comings of the 2D model, which was only used to predict the in-plane behavior but completely ignored the out-ofplane behavior [35]. A tetrakaidecahedra 3D model for foam cell was designed by Lakes and Witt [39] as shown in Figure 9a&b.

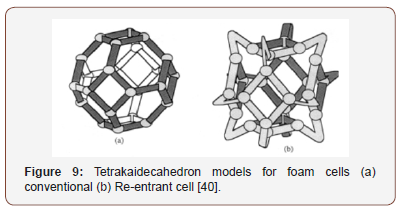
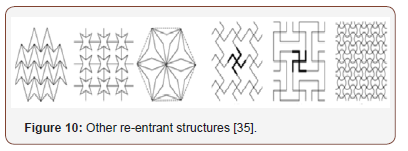
The 3D re-entrant cell resulted when a conventional 3D cell structure was transformed by protruding the ribs of the structure inwardly, so that the ribs in lateral direction will tend to move out when tension is placed on the vertically protruding ribs leading to lateral expansion. And when the structure is compressed, the ribs further bends inward which result in lateral contraction [35]. As a result of this development, auxetic polymer foams have been well understood. Other re-entrant structures as shown in Figure 10 includes the double- arrowhead, star-honeycomb structure, structurally hexagonal re-entrant honeycomb, Structure formed from lozenge grids, Structure formed from square and Structure formed from sinusoidal ligaments respectively.

In a research work conducted by [15] one of the first researchers to propose a star-shaped microstructure, he employed a numerical homogenization approach in his work. The mechanism of the auxetic characteristics of this star-shaped structure is represented in Figure 10a, and the Poisson’s ratio is -1, while their analytical Young’s modulus is;

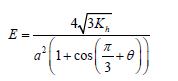
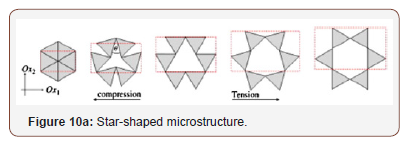
Where a is the length of the sides,θ is the hinging angle, and K_h is the force constant due to hinging. Both the Poisson’s ratio υ and the Young’s modulus E are independent of the direction of the loading [8].

In addition to the previous, [41,42] developed star-shaped structures from general isosceles triangles, as shown in Figure 10b.

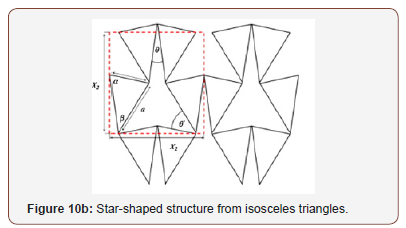
The Poisson’s ratios for loading in the ox₁ or ox₂ are:

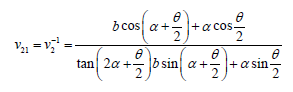
From the equation, one can adjust the Poisson’s ratio by adjusting the values of both and. it can be easily deduced from the trigonometric relation of;

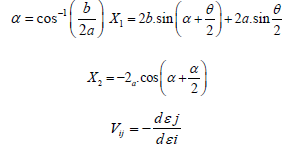
Whereα , X₁ and X ₂ are as shown in Figure 10a

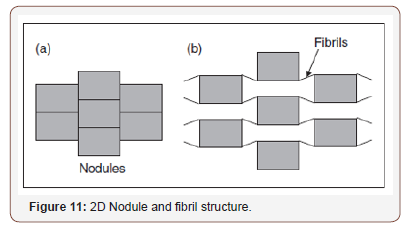
Nodule and fibril structure

As the name implies, this model is basically made of interconnected network of nodules and fibrils. It was first reported by Caddock and Evans for auxetic micro-porous polymer in a 2D model [35]. When loaded, the translation of the nodules connected by the stretched fibrils results in the structure’s auxetic behavior. In other words, the fibrils cause lateral nodule translation when loaded, leading to a strain-dependent negative Poisson’s ratio [43]. Aside the 2D model, nodule and fibril structure also exist in a 3D form and investigations according to [35] showed that the 3D hexagonal nodule and fibril models exhibited a greater NPR effect as compared to the 2D ones. Figure 11 illustrates a 2D nodule and fibril structure.

Mechanical properties of auxetic materials

As compared to conventional materials, auxetic materials have many enhanced properties which enable them to have a variety of uses. This part of the review focuses on the mechanical properties of these auxetic materials.

Indentation behavior

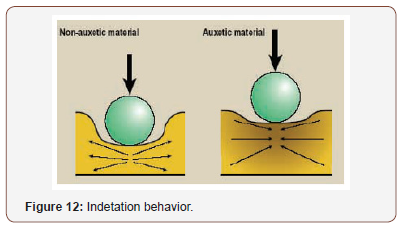
Isotropic auxetic materials are considered to have a greater indentation resistance due to their negative Poisson’s ratio. Usually when a conventional material is subjected to indentation, the force/ load applied compresses the material. The material then compensates the pressure by spreading perpendicular to and away from the direction of the applied force/load. Nevertheless, auxetic materials when indentation occurs, the material contracts (i.e. the material flows to the vicinity of the impacted load), creating an area of denser materials with a higher resistance to indentation [40]. Figure 12 shows the indentation behavior between a non-auxetic and auxetic material respectively.

An example of this property could be found in the auxetic microporous ultra-high molecular weight polyethylene (UHMWPE) which was improved and enhanced to a factor of 2 over conventional UHMWPE [44]. Again [45] propounded in their experiment to verify the strain dependent densification of auxetic foam, that the auxetic specimen demonstrate an enhanced indentation resistance independent of bulk density and modulus. Their results showed that auxetic foams densify under indentation and the strain field under the indenter is much larger, probably due to enhanced shear stiffness [32]. The increase in indentation resistance can be justified by the theory of elasticity. Furthermore, the material hardness (H) is associated with the indentation resistance and it is correlated to Poisson’s ratio by the equation below;

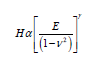
where E is the Young’s modulus, ν is the Poisson’s ratio of the base materials and γ is the constant that assumes the value 1 or 2 / 3 in the case of uniform pressure distribution or Hertzian indentation, respectively [40]. It can be inferred by analyzing the equation, that for 3D isotropic materials, when the Poisson’s ratio decreases to the extreme values near −1, the hardness of the material tends to infinity [46].

Fracture toughness and resistance to crack

Fracture resistance increases best in materials that processes a negative Poisson’s ratio (auxetic materials). Again they have low crack propagation and therefore needs much energy to expand them [47]. The fracture behavior of both conventional and reentrant foam in tension is brittle-like. An experiment was conducted to investigate the toughness of an auxetic foams as a function of the permanent volumetric compression ratio [48]. A crack growth observation was conducted by [49], who demonstrated that the stress intensity factor for conventional foams K_*IC is proportional to the normalized density and can be described by the equation;

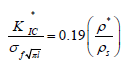
Where is the fracture stress of the cell rib, l is the rib length, ρ * is the foam density and ρ_s is the density of the foam-based material [40]? The work of Choi and Lakes afterwards showed that in the case of re-entrant foam cannot be applied and the stress intensity factor for this kind of foams could be expressed by the equation;

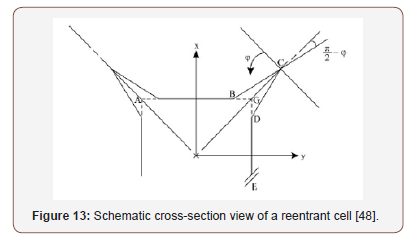
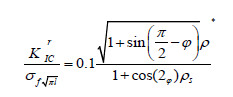
Where is the rib angle of the re-entrant cell illustrated in Figure 13.

It was observed in the same work by Choi and Lakes that, the relationship between stress intensity factors in the analyzed reentrant foam could be established according to this equation;

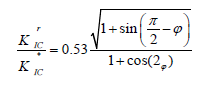
Compared to that of conventional polyurethane-polyester foam materials [32], the toughness of auxetic foam was increased by factors80%, 130% and 160% for permanent volumetric compression ratios of 2.0, 2.5, 3.0, respectively [35]. The fracture toughness of auxetic foams was observed to be greater than that of conventional foams, even though they have a smaller Young’s modulus. Due to negative Poisson’s ratio, a crack under load in an auxetic material will expand and close up, indicating the materials ability to resist crack.

Synclastic curvature

The ability of a material or a body to deform into forming a dome shape when bent is referred to as the Synclasticbehaviour of that material. Generally, when a material is bent, it is subjected to compression and tensile stress which causes the deformation of the material. Unlike conventional material which when bent forms a saddle shape indicating an anti-clastic curvature [32], auxetic materials when bended, expands exteriorly and contracts interiorly [40]. This expansion and contraction that occur in the auxetic material give rise to its deformation into a dome shape. Auxetic material has the ability to form a doubly curved shape which helps in an easy production of a dome shape without the need for excessive machining or forcing the material to take up the desired shape which could result in possible damage. Figure14 shows the anti-clastic and Synclastic nature of a conventional and auxetic material respectively.

Energy absorption

Auxetic materials are notable of having better energy absorption properties. Compared to conventional materials, auxetics are able to absorb superior energies such as ultrasonic, acoustic and damping. Baker CE [50] experimented on the sound absorption of an auxetic foam coated with magnetorheological (MR) fluid over a conventional foam. It was observed that the auxetic PU foam shows an enhanced crashworthiness properties and increased sound absorption characteristics (at low frequencies). A cyclic compression test on auxetic foam indicates that the damping capacity of auxetic foams was 10 times higher than that of the original conventional foams which were used in the formulation of the auxetic foams [51].

Variable permeability

Auxetic materials have been proved by [52] to have a unique poreopening which enable them to offer improved filter performance from the macro-scale to the nano-scalefilter performance from the macro-scale to the nano-scalefilter performance from a macroscale to a nano-scale. The pores of auxetic materials become wider in both axial and perpendicular direction when stretched. These unique characteristics can help overcome the reduction in filtration efficiency and increased pressure across the filter due to the pores blocked. A study was made on auxetic honeycomb and it was found that the variable permeability could be improved from macro-scale to nano-scale [8].

The application of auxetic materials cuts across a number of sectors due to the negative Poisson’s ratio they possess. They find application in textile sector, biomedical, aerospace, industries and many others.

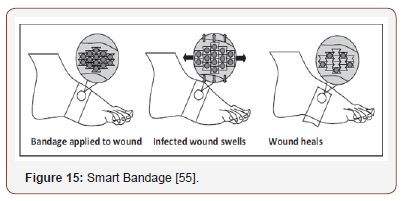
An auxetic material due to its pore structure as in the case of re-entrant honeycomb which opens when stretched enables the material to compensate pressure and also enhance de-fouling [53], making it the best candidate for filtration [8]. From the medical point of view, auxetic materials could be used as spinal implants [54], esophageal stent, artificial blood vessels [9], also in smart bandages. These bandages are produced from auxetic filaments and are capable of carrying healing agents for wounds. When the bandage is applied on a swelled wound, the bandage tends to stretch and open, releasing the wound-healing agents and after the wound has healed and the swelling decreased to normal, the bandage then closes up, stopping the release of the agents [35] as shown in Figure 15.

In aerospace application, auxetic materials are used as vanes for gas turbine engines [56], auxetic gradient cellular core for aero-engine fan blades [57], aircraft nose-cones and many others. Auxetic materials are more sensitive due to their low bulk modulus and therefore can be used as sensors such as hydrophones [58].

Auxetic materials are used in sensors and actuator applications. For instance, piezoelectric composites consist of piezoelectric ceramic rods within a passive polymer matrix and are used in medical ultrasonic imagers and hydrophone receivers of naval sonar [9]. Auxetic polymer matrix was preferred to a non-auxetic polymer matrix in a recent design [59] by Smith of the US Office of Naval Research to optimize the performance of this piezocomposite device as shown in Figure 16.

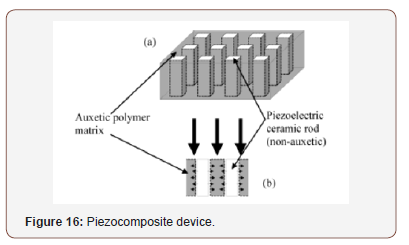
The auxetic polymer matrix contracts laterally in response to a compressive load incident on the surface of the device. This contraction allows free lateral expansion of the ceramic rods, leading to enhanced electromechanical coupling of the device, which is crucial in the overall device performance. Unlike the auxetic polymer matrix which converts the compressive planar stress into a compressive longitudinal stress and therefore reinforces the incident vertical compressive stress, the non-auxetic polymer matrix converts a compressive planar stress into a tensile longitudinal stress, which acts to diminish the incident vertical compressive stress [60].

In the textile field auxetic materials being it auxetic filaments, yarns and/or auxetic fabrics have a wider application. Auxetic fabrics due to their ability to absorb energy are used in protective clothing and equipment for most sporting activities that involves dangerous injuries such as riding, racing and skating, to protect wearers from injuries by impact forces [35]. These protective wears protect the venerable parts of the body such as the elbows and knees and other parts of the body and are also considered as a good candidate for producing bulletproof vest, since the force of the bullet can be reduced by the sideways expansion of the auxetic vest [61]. They are sometimes combined with other materials produce some protective wears like crash helmet, bullet proof vest, shin pad, knee pad or glove [32]. Aside their energy absorbing ability their Synclastic nature allows them to form a dome shape when bent making them easy to conform to the shape of an elbow and the other venerable body parts.

Auxetic 3D spacer fabrics due to their air permeability are used as replacements for conventional foam fabrics in the production of protective wears.

In the case of maternity dresses, the most common ones on the market are mostly made of elastic fabrics for the belly or adjustable waist which when worn impacts pressure from time to time on the belly as it grows. Using auxetic fabrics in producing the maternity wears solves the problem of discomfort. The auxetic fabric becomes wider as the belly grows in both waist direction and the direction perpendicular to it, and it forms a dome shape perfectly to fit the belly so that it wouldn’t have to bare more pressure as it should.

Auxetic materials are used in the manufacturing of chiralbased honeycomb deployable antennas due to their shape-memory properties [62] for deep space missions. During transportation, these antennas are folded since the area for rocket launchers is limited. In space, the shape-memory structure unfolds to its original size using the thermal energy absorbed from the sun. Figure 17 shows the auxetic chiral-based honeycomb deployable antenna in a folded and unfolded state respectively.

The counter-intuitive nature of auxetic materials has given it much popularity in recent years. A number of researchers have been made purposely to investigate the deformational mechanism of its internal structure as well as its potential applications across various fields. Studies so far have unveiled the unique mechanical properties of auxetic materials including, indentation resistance, fracture toughness, Synclastic curvature, variable permeability and energy absorption. These unique properties have generated a series of advantages and have expanded the scope for the application of auxetic materials. For example, auxetic materials according to [63] have been identify as a candidate material to be used in electromagnetic launcher technology. However, auxetic material due to its porosity exhibit low stiffness. The development of molecular auxetics which incorporates nanotechnology to produce auxetic Nano-materials could be one way to solve this problem. In this case, the auxetic Nano-material will have a high modulus.

With further studies and contribution from researchers, it is believed that auxetic materials in the future have the ability to improve and to making the development of new functional and structural materials a reality.

None.

No Conflict of Interest.

1. Pozniak AA, Wojciechowski KW (2014) Poisson’s ratio of rectangular anti‐chiral structures with size dispersion of circular nodes. physica status solidi 251(2): 367-374.
2. Hu H, Wang Z, Liu S (2011) Development of auxetic fabrics using flat knitting technology. Textile Research Journal 81(14): 1493-1502.
3. Voigt W (1893) Bestimmung der Elasticitätsconstanten für das chlorsaure Natron. Annalen der Physik 285(8): 719-723.
4. Lakes R (1987) Foam structures with a negative poisson’s ratio. Science 235(4792): 1038-1040.
5. Wan H, Ohtaki H, Kotosaka S, Hu G (2004) A study of negative poisson’s ratios in auxetic honeycombs based on a large deflection model. European Journal of Mechanics-A/Solids 23(1): 95-106.
6. Gatt R, Mizzi L, Azzopardi JI, Azzopardi KM, Attard D, et al. (2015) Hierarchical auxetic mechanical metamaterials. Scientific reports 5: 8395.
7. Grima JN, Alderson A, Evans KE (2005) Auxetic behavior from rotating rigid units. Physica status solidi 242(3): 561-575.
8. Prawoto Y (2012) Seeing auxetic materials from the mechanics point of view: a structural review on the negative poisson’s ratio. Computational Materials Science 58: 140-153.
9. Evans KE, Alderson A (2000) Auxetic materials: functional materials and structures from lateral thinking! Advanced materials, 12(9): 617-628.
10. Grima JN, Farrugia PS, Gatt R, Attard D (2008) On the auxetic properties of rotating rhombi and parallelograms: a preliminary investigation. physica status solidi 245(3): 521-529.
11. Prall D, Lakes R (1997) Properties of a chiral honeycomb with a Poisson’s ratio of -1. Int J of Mechanical Sciences 39(3): 305-314.
12. Spadoni A, Ruzzene M, Scarpa F (2005) Global and local linear buckling behavior of a chiral cellular structure. physica status solidi 242(3): 695- 709.
13. Gibson LJ, Ashby MF, Schajer GS, Robertson CI (1982) The mechanics of two-dimensional cellular materials. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 382(1782): 1-244.
14. Lee J, Choi J, Choi K (1996) Application of homogenization FEM analysis to regular and re-entrant honeycomb structures. Journal of Materials Science 31(15): 4105-4110.
15. Theocaris PS, Stavroulakis GE, Panagiotopoulos PD (1997) Negative Poisson’s ratios in composites with star-shaped inclusions: a numerical homogenization approach. Archive of Applied Mechanics 67(4): 274- 286.
16. Lim TC (2003) Constitutive relationship of a material with unconventional poisson’s ratio. Journal of materials science letters, 22(24): 1783-1786.
17. Grima JN, Alderson A, Evans KE (2005) An alternative explanation for the negative Poisson’s ratios in auxetic foams. Journal of the Physical Society of Japan 74(4): 1341-1342.
18. Milton GW (1992) Composite materials with Poisson’s ratios close to-1. Journal of the Mechanics and Physics of Solids 40(5): 1105-1137.
19. Hine PJ, Duckett RA, Ward IM (1997) Negative Poisson’s ratios in angleply laminates. Journal of materials science letters 16(7): 541-544.
20. Ishibashi Y, Iwata M (2000) A microscopic model of a negative Poisson’s ratio in some crystals. Journal of the Physical Society of Japan 69(8): 2702-2703.
21. Liu Y, Hu H (2010) A review on auxetic structures and polymeric materials. Sci Res Essays 5(10): 1052-1063.
22. Grima J, Evans K (2000) Auxetic behavior from rotating squares. Journal of Materials Science Letters 19(17): 1563-1565.
23. Grima JN, Zammit V, Gatt R, Alderson A, Evans KE (2007) Auxetic behavior from rotating semi‐rigid units. physica status solidi 244(3): 866-882.
24. He C, Liu P, McMullan PJ, Griffin AC (2005) Toward molecular auxetics: Main chain liquid crystalline polymers consisting of laterally attached para‐quaterphenyls. physica status solidi 242(3): 576-584.
25. Kolla A, Ju J, Summers JD, Fadel G, Ziegert JC (2010) Design of chiral honeycomb meso-structures for high shear flexure. ASME Proceedings, 36th Design Automation Conference: 43-49.
26. Alessandro S, Fabrizio S, Massimo R, Lew TL (2005) Chiral hexagonal cellular sandwich structure: a vibro-acoustic assessment. in Smart Structures and Materials. International Society for Optics and Photonics.
27. Wojciechowski KW (1989) Two-dimensional isotropic system with a negative Poisson ratio. Physics Letters A 137(1-2): 60-64.
28. Alderson A, Alderson KL, Attard D, Evans KE, Gatt R, et al. Elastic constants of 3-, 4-and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading. Composites Science and Technology 70(7): 1042-1048.
29. Grima JW. Miller N, Ravirala, Smith C, Zied K (2010) Elastic constants of 3-, 4-and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading.
30. Lakes R (1991) Deformation mechanisms in negative Poisson’s ratio materials: structural aspects. Journal of Materials Science 26(9): 2287- 2292.
31. Shilko SV, Petrokovets EM, Pleskachevsky YM (2008) Peculiarities of friction in auxetic composites. physica status solidi 245(3): 591-597.
32. Liu Y, Hu H (2010) A review on auxetic structures and polymeric materials. Scientific Research and Essays. 5(10): 1052-1063.
33. Grima JN, Evans KE (2006) Auxetic behavior from rotating triangles. Journal of materials science 41(10): 3193-3196.
34. Alderson A, Evans KE (2002) Molecular origin of auxetic behavior in tetrahedral framework silicates. Phys Rev Lett 89(22): 225503.
35. Wang Z, Hu H (2014) Auxetic materials and their potential applications in textiles. Textile Research Journal 84(15): 1600-1611.
36. Aldred PL, Moratti S (2005) Dynamic simulations of potentially auxetic liquid-crystalline polymers incorporating swiveling mesogens. Molecular Simulation 31(13): 883-887.
37. Lira C, Innocenti P, Scarpa F (2009) Transverse elastic shear of auxetic multi re-entrant honeycombs. Composite Structures 90(3): 314-322.
38. Bezazi A, Scarpa F, Remillat C (2005) A novel centresymmetric honeycomb composite structure. Composite Structures 71(3): 356-364.http://homepages.cae.wisc.edu/~lakes/PoissonEduc.pdf
39. Lakes R, Witt R (2002) Making and characterizing negative Poisson’s ratio materials. International Journal of Mechanical Engineering Education 30(1): 50-58.
40. Carneiro VH, Meireles J, Puga H (2013) Auxetic materials-A review. Materials Science-Poland 31(4): 561-571.
41. Grima JN, Gatt R, Ellul B, Chetcuti E (2010) Auxetic behavior in noncrystalline materials having star or triangular shaped perforations. Journal of Non-Crystalline Solids 356(37): 1980-1987.
42. Grima JN, Gatt R, Alderson A, Evans KE (2005) On the potential of connected stars as auxetic systems. Molecular Simulation 31(13): 925- 935.
43. Liu Q (2006) Literature review: materials with negative Poisson’s ratios and potential applications to aerospace and defence. DTIC Document pp. 1-47.
44. Alderson KA, Pickles AP, Neale PJ, Evans KE (1994) Auxetic polyethylene: the effect of a negative Poisson’s ratio on hardness. Acta Metallurgica et Materialia 42(7): 2261-2266.
45. Smith CW, Lehman F, Wootton RJ, Evans KE (1999) Strain dependent densification during indentation in auxetic foams. Cellular polymers 18(2): 79-101.
46. Critchley R, Corni I, Wharton JA, Walsh FC, Wood RJ, et al. (2013) A review of the manufacture, mechanical properties and potential applications of auxetic foams. physica status solidi (b) 250(10): 1963-1982.
47. Choi JB, Lakes RS (1992) Non-linear properties of polymer cellular materials with a negative Poisson’s ratio. Journal of Materials Science 27(17): 4678-4684.
48. Choi JB, Lakes RS (1996) Fracture toughness of re-entrant foam materials with a negative Poisson’s ratio: experiment and analysis. International Journal of fracture 80(1): 73-83.
49. Maiti SK, Ashby MF, Gibson LJ (1984) Fracture toughness of brittle cellular solids. Scripta Metallurgica 18(3): 213-217.
50. Scarpa F, Smith FC (2004) Passive and MR fluid-coated auxetic PU foam–mechanical, acoustic, and electromagnetic properties. Journal of intelligent material systems and structures 15(12): 973-979.
51. Scarpa F, Ciffo LG, Yates JR (2003) Dynamic properties of high structural integrity auxetic open cell foam. Smart Materials and Structures 13(1): 49.
52. Alderson A, Rasburn J, Evans KE, Grima JN (2001) Auxetic polymeric filters display enhanced de-fouling and pressure compensation properties. Membrane Technology 2001(137): 6-8.
53. Alderson A, Rasburn J, Ameer-Beg S, Mullarkey PG, Perrie W (2000) An auxetic filter: a tuneable filter displaying enhanced size selectivity or defouling properties. Industrial & engineering chemistry research 39(3): 654-665.
54. Baker CE (2011) Auxetic spinal implants: consideration of negative Poisson’s ratio in the design of an artificial intervertebral disc. University of Toledo, USA.
55. Alderson K, Webber R, Kettle A, Evans K (2005) Novel fabrication route for auxetic polyethylene. Polymer Engineering & Science, 45(4): 568- 578.
56. Nakamura M (1995) Fundamental Properties of Intermetallic Compounds. MRS Bulletin 20(8): 33-39.
57. Lira C, Scarpa F, Rajasekaran R A gradient cellular core for aeroengine fan blades based on auxetic configurations. Journal of Intelligent Material Systems and Structures 22(9): 907-917.
58. Smith WA (1998) Composite piezoelectrics utilizing a negative Poisson ratio polymer. The Journal of the Acoustical Society of America.
59. Smith WA (1991) Optimizing electromechanical coupling in piezocomposites using polymers with negative Poisson’s ratio. Ultrasonics Symposium Proceedings IEEE.
60. Gibiansky LV, Torquato S (1997) On the use of homogenization theory to design optimal piezocomposites for hydrophone applications. Journal of the Mechanics and Physics of Solids 45(5): 689-708.
61. Nagai K (1994) Narrow passage moving body structure. Patent JP06137799, Japan.
62. Jacobs S, Coconnier C, DiMaio D, Scarpa F, Toso M (2012) Deployable auxetic shape memory alloy cellular reflector demonstrator: design, manufacturing and modal testing. Smart Materials and Structures 21(7).
63. Persad C (1999) Progress in materials for EML: Review and preview. IEEE transactions on magnetics 35(1): 300-306.