Software TexMath For Mechanical Textile Simulation at the Yarn Level

A tool for the mechanical simulation of textiles at the yarn level, incorporating mesh redistribution through frictional sliding between yarns, is presented. The fabric properties are computed based on experimentally obtained mechanical properties of yarns and the specified textile pattern or machine parameters used during fabric production. The outputs include textile tension, bending, torsion, and compression properties. This tool can be applied to draping simulations, sensitivity studies, design optimization, and the translation of results into machine control parameters for knitting or weaving machines.

Keywords:Mechanical simulation of textiles at the yarn level; Continuous fibers in frictional contact; Integrated electro-light yarns and wires; 3D printing on textiles; Seams; Textile strength

The focus of this paper is TexMath, an in-house developed, GUI-based software designed to simulate textile behavior based on yarn properties and fabric structure. The software employs the following strategy:
• Generation of detailed 3D-textile structures for warp and weft knits, as well as woven, based on textile machine formats;
• Input of the force-strain tensile curve or Young’s modulus for each yarn;
• Rapid computation (within seconds) of textile properties, including bending, torsion, tension, shear, and compression;
• Optimization of textile structures with respect to product specifications;
• Control of the textile machine to produce the optimized product.

One of the primary inputs for the software is force-strain diagrams for yarns, which are typically obtained through tensile tests. Yarn suppliers often provide such data with their products. However, yarns may consist of several similar or different filament bundles, wound together with or without pre-strain, and using varying winding directions and periods. In these cases, TexMath can perform a preliminary step to calculate the effective properties of the composite yarn.

The input parameters for the simulation include the number and direction of filament bundles, the winding period, their thickness, and the force-strain diagrams for each type of bundle. Figure 1 illustrates the sensitivity of composite yarns to the number of monofilaments or bundles while maintaining the same material quantity.

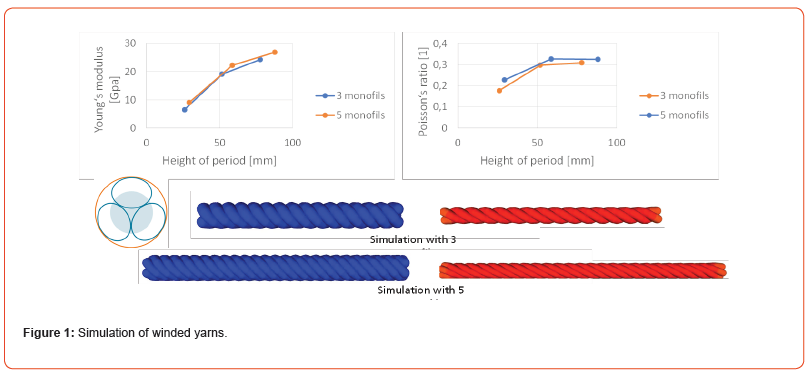
The outputs of the simulation include the tensile stiffness (or force-strain curve) and the Poisson’s ratio of the composite yarn. Such simulations can be particularly useful for optimizing inlay yarns in compressive wear. For example, an elastin yarn can be placed in the center, with less stretchable knitting bundles wound around it. This configuration increases the yarn’s roughness and creates a “smart” yarn that remains soft up to a certain threshold and then becomes stiff.

TexMath simulations enable the optimization of such yarns to adjust this threshold in relation to the desired shape and size required for draping. The tool can also account for different prestrains in individual bundles (Figure 2).

In many applications, wound yarns are thermos-fixed, which results in their helical initial shape. When subjected to tensile loading or pre-strain, these yarns begin to bend and twist. Such effects can be captured and modeled using the software, and further optimized to achieve the desired outcome.

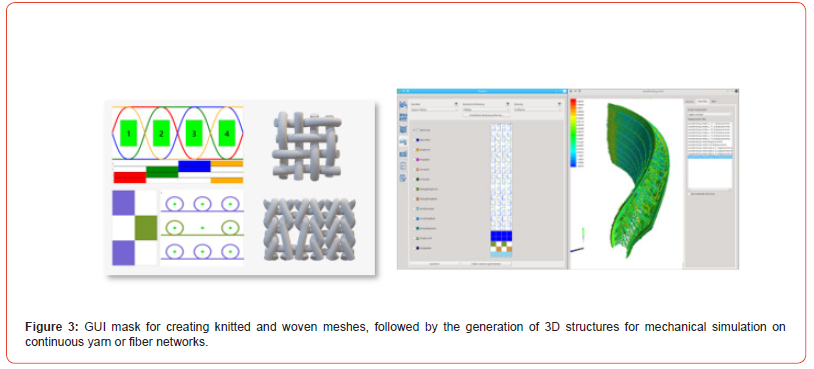
The TexMath pattern creation tool for weft-knitted fabrics uses the same input format as the Karl-Mayer and SHIMA SEIKI knitting machines. The woven input mask follows the format of woven machines, while the warp-knitted input also utilizes the common sign system, as shown in Figure 3.

The software can also be applied to non-woven textiles, as long as their structure is represented in terms of a graph with nodes and contact points. This can be achieved, for example, by using artificial intelligence (AI) based on statistical parameters of the non-woven material, which can be derived from the production process or obtained through image analysis.

The primary functionality of the TexMath software is to compute the effective properties of textile shells and membranes. For stretchable textiles, the tensile properties are calculated for each type of yarn and knitted pattern used. The tool allows for virtual substitution of yarns or adjustments to the mesh size or knitting pattern, enabling the achievement of the desired textile stretching without the need for costly trial-and-error experiments.

The software also provides bending and torsion properties of the textile and visualizes the local stresses and displacements in the yarns under loading. This allows for the estimation of the textile’s strength, near the seams, 3D prints, wires, etc., as shown in Figure 4.

The software can be used for the sensitivity study on the design parameters and is many times experimentally validated in many types of applications, see Figure 5.

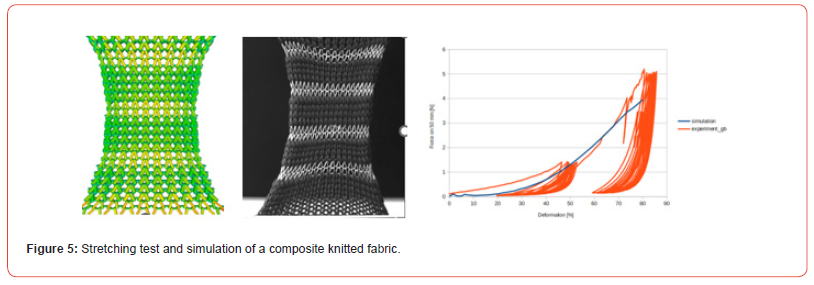
One of the input parameters for the simulation is the friction coefficient between yarns, which is difficult to measure and typically not provided with the yarns. For many types of yarns, its value is chosen by default based on data collection and interpolation.

The software allows users to place fixations along specified boundaries, user-defined lines, or subdomains, and to apply forces and pre-strains to the yarns. A key feature of this software is the modeling of contact sliding between yarns and the mesh redistribution in the textile under tension. This alters the textile’s effective properties, including its macroscopic folding and other behaviors. Such redistribution can occur locally, near the applied loading or other stress concentration factors. Using TexMath can help avoid excessively large holes or inhomogeneities in the fabric, as shown in Figure 6.

Finally, the software can be used for draping simulations, as shown in Figure 7. In the first two figures, a knitted mask is extended at six points and then moved toward the face. The yarns do not penetrate the face but instead slide over its surface. Users can control the local mesh deformations and stresses in the yarns through the GUI.

The last of the Figures 7 simulates an effective textile that folds under its own weight on a cube. This part of the software is currently under development and is not included in the current version (V 1.5.0) of TexMath.

Optimal control of circular knitting machine

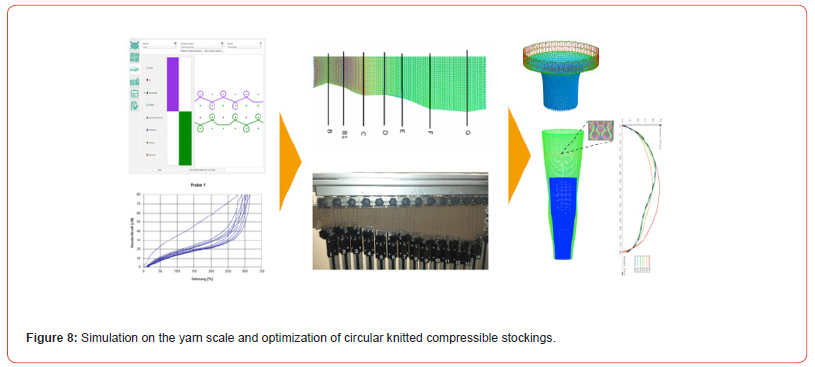
Simulation-assisted design of patient-specific compressible stocking production (Figure 8) is one successful application example of the efficient and fast simulation algorithms used in TexMath. These algorithms are based on dimensional reduction techniques and the homogenization of thin periodic structures.

The computational strategy can be summarized in the following steps:
• Design the pattern.
• Insert force-strain curves and friction coefficients for the yarns.
• Simulate and compare the results with standard mechanical experiments.
• Virtually drape the stocking on a specific leg.
• Optimize the mesh size of each row with respect to the required pressure profile along the leg axis.
• Map the results onto production machine parameters for each row and adapt them to each specific knitting machine.
• Control the knitting machine to produce a patient-optimized stocking.

The use of such a software tool drastically reduces the number of mechanical tests required and allows for the replacement of any existing yarn with a new one, or the modification of the inlay, or its integration in a different manner. Since the mesh size varies across the stocking, it can be time-consuming and expensive to optimize the entire stocking for even a slightly different yarn, just experimentally.

Topology optimization: reinforcing stretchable textiles by 3D printing or dense fabric structures

The final example demonstrates the applicability of TexMath simulations to replace stretchable membranes with shaped shells, aimed at reducing local stresses in certain parts of the draped membrane, as shown in Figure 9.

The design space for the optimization should be selected according to the available technology. This can be achieved by doubling the yarns used in the subdomains that need reinforcement. Alternatively, a dense knitting pattern could be employed, or some substructures can be 3D printed on the textile to improve the fit to the surface.

The numerical tool TexMath [1] for mechanical simulations of textiles at the yarn level is presented here. This tool can be used for sensitivity studies with respect to different yarns, mesh sizes, and other parameters, potentially reducing the number of required experiments. It can also assist in the design of new products or the optimization of existing ones, as demonstrated in our recent publications [2-7]. TexMath is based on dimensional reduction techniques and the homogenization of thin periodic structures, developed within our working group at Fraunhofer ITWM over the past 15 years through numerous PhD works.

None.

Authors declare no conflict of interest.

1. Orlik J, Neusius D, Steiner K (2024) Modelling and Simulation of Technical Textiles by TexMath. Fraunhofer Institute for Industrial Mathematics.
2. Orlik J, Neusius D, Krier M, Steiner K, Backes S, et al. (2024) Wrinkling Controlled Shear and Draping, Based on Hierarchical Textile Models, Weaving Kind and Yarn Properties. Textiles 4(4): 582-595.
3. Rotzler S, Orlik J, von Krshiwoblozki M, Neusius D, Steiner K (2025) Simulation based optimization of textile integrated circuits and conductors. Results in Engineering S: 103857.
4. Orlik J, Neusius D, Steiner K, Krier M (2024) On the ultimate strength of heterogeneous slender structures based on multi-scale stress decomposition. International Journal of Engineering Science 195: 104010.
5. Krier M, Krier M, Orlik J, Panasenko G, Steiner K (2024) Asymptotically proved numerical coupling of a 2D flexural porous plate with the 3D Stokes fluid. Multiscale Modeling & Simulation 22 Jg Nr. 4S: 1608-1645.
6. Orlik J, Panasenko G, Shiryaev V (2016) Optimization of textile-like materials via homogenization and beam approximations. Multiscale Model. Simul 14: 637-667.
7. Wackerle S, Pinnau R, Orlik J (2018) Optimization of buckling for textiles. In Progress in Industrial Mathematics at ECMI; Springer: Budapest, Hungary.