Fundamental Principles of Theory of Gyroscopic Effects

In the initial stages of the history of mechanics, specific properties of rotating objects were studied by famous scientists. The development of the theory of spinning bodies ensued from the works of I. Newton, J.L.R. D’Alembert , Lagrange , L. Poinsot , L. Foucault, S.D. Poisson, Lord Kelvin, and other famous scientists and researchers. The French mathematician P.-S. Laplace was the first that propose some type of gyrocompass that insensitive to a magnetic field. Other brilliant scientists investigated, developed, and added new interpretations of the gyroscopic effects, as displayed in the rotor’s persistent maintenance of its plane of rotation.

The theory of the motion of rigid bodies written by the mathematician L. Euler did a great contribution to the theory of gyroscopes, but could not describe all gyroscopic effects. The gyroscopic effects of a self-balancing fast-spinning body around its symmetry axis attracted the attention of many outstanding scientists. The applied theory of gyroscopes emerged mainly in the twentieth century. Nevertheless, known gyroscope theories (G. Greenhill 1914, J. B. Scarborough 1958) have not been clearly distinguished from theoretical principles formulated in past centuries, and present a simplified treatment of gyroscopic effects [1]. All known gyroscopic theories do not match practice, i.e. there has not been a complete gyroscope theory for centuries. This fact is an unusual phenomenon in the science of classical mechanics that can solve more complex problems than inertial torques acting on a simple rotating disc and its motions [2, 3]. For engineering problems, researchers have developed the numerical modeling of the gyroscopic effects, which were later used for the software [4].

The gyroscope theory is a very important aspect of the dynamics of rotating objects. Gyroscopic effects are relayed in many engineering calculations of rotating parts, and deriving a complete gyroscope theory is a crucial challenge. The known gyroscope theories are one of the most complex and intricate in terms of analytic solutions. The modeling of gyroscopic motions in Lagrange’s equations, 3-D presentation, is based on severe mathematics and software. Researchers of the gyroscopic effects intuitively pointed out that inertial forces act in gyroscopic effects and invented artificial terms. These expressions are gyroscopic couples, resistance, and precessions, and are attributed to fantastic properties as a non-inertial and non-gravitational system, etc. Such delusions originated from the absence of mathematical models relating to the inertial forces acting on a rotating object. This is the reason that for centuries, researchers tried to resolve gyroscopic problems via intricate theories. Since the Industrial Revolution, probably tons of publications and dozens of theories have been dedicated to gyroscopic effects. Even today, every year, around a hundred manuscripts with solutions to gyroscopic problems are published in journals. This fact demonstrates that gyroscopic effects remain unsolved until recent times.

Today, industries show designs of new gyroscopes in which physical principles are different and represented by mechanical, electronic, laser, optic, quartz, and integrating systems with various technical features and work [5-9]. The several indicators of gyroscopes determine their scope in industries, characteristics, and factor stability, in which the primary problem is related to the error in measuring the angular velocity [7]. The proposed gyroscope theory is based on mathematical models, which describe the forces and motions acting on the mechanical gyroscope by fundamental principles of classical mechanics [7].

Engineering machines and mechanisms contain rotating objects of unique designs that manifest gyroscopic effects. All of them generate inertial forces and torques acting on their components the physics of origination was not described in full scale until our time. Recent studies show rotating masses of the movable object produce centrifugal and Coriolis forces and torques, in addition to the change in the angular momentum that is linked with the geometry of the rotating objects. The method of causal investigatory dependency formulated the mathematical models for the inertial torques gendered by the rotating objects. The numerous designs of rotating objects present a challenge for the researchers that should derive the mathematical models for their inertial torques whose action manifests gyroscopic effects.

The rotating masses of the spinning objects produce the system of inertial torques whose action manifests gyroscopic effects. The centrifugal, Coriolis, forces, and the change in the angular momentum generated by the rotating masses constitute one part of the fundamental principles of gyroscope theory. The method for deriving mathematical models for inertial torques of any designs of rotating objects can describe the physics of their gyroscopic effects. This method was used for analytical modeling of the spinning disc motions under the action of the external load. Analysis of its motions shows that the center mass and mass elements of the spinning disc produce several inertial forces. The rotating masses of the spinning disc generate the centrifugal, and Coriolis forces, which components act as the torque and torque of the change in the angular momentum acting around the two axes of the disc motions. The action of the inertial torques is described in detail in the theory of gyroscopic effects.

The action of the inertial torques and rotations of the spinning disc axes are shown at the moveable 3D Cartesian coordinates in (Figure 1).

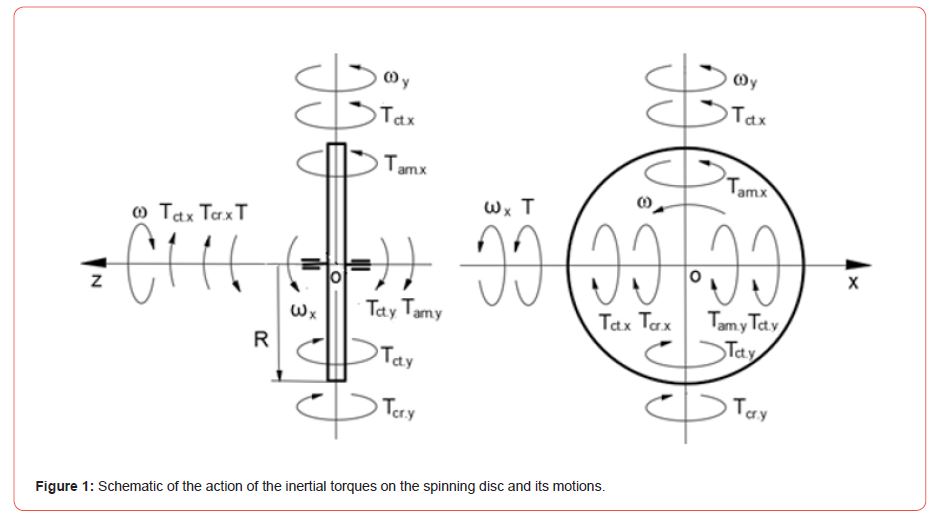
Figure 1 contains the following information.

•The action of the external T generates the initial resistance inertial torques of the centrifugal T_ct.x, Coriolis T_cr.x forces acing around axis ox, and the precession torques of the centrifugal T_ct.x, and the change in the angular momentum T_am,x acting around axis oy.

•The initial inertial torques acting around axis oy generate the resistance inertial torques of the centrifugal T_ct.y, and the change in the angular momentum T_am,y acting around axis oy.

•The resulting toque of axis oy generates the precession torques of the centrifugal T_ct.y, and the change in the angular momentum T_am,y acting around axis ox, which is added to the initial resistance inertial torques of the centrifugal T_ct.x, Coriolis T_cr.x forces.

•The resulting torque of axis ox generates the corrected precession torques of the centrifugal T_ct.x, and the change in the angular momentum T_am,x acting around axis oy.

•Around each axis, ox and oy are acting for inertial toques, which are feedback looped. Any change in the inertial toques about one axis leads to a change in the inertial toques about the other axis. The action of the inertial toques expresses the interrelated motions of the spinning disc around the two axes. This fact means the kinetic energies of inertial toques about two axes are equal and based on the principle of mechanical energy conservation.

•The system of the inertial toques and the interallied motions of the spinning disc constitutes the fundamental principles of the theory of gyroscopic effects (Table 1).

Table 1 shows the value of Euler’s change in the angular momentum which is less than ten percent among the value of other inertial torques, whose action significantly (over 91 percent) prevails in the manifestation of gyroscopic properties. Nevertheless, the textbooks of classical mechanics continue to solve gyroscopic effects by Euler’s principle of the change in the angular momentum [5-10]. The derived method for the mathematical modeling of gyroscopic effects is holistic and should be used for computing the inertial toques and the interrelated motions of the spinning objects for any design of rotating parts in engineering.

Table 1: Fundamental principles of the gyroscope theory.

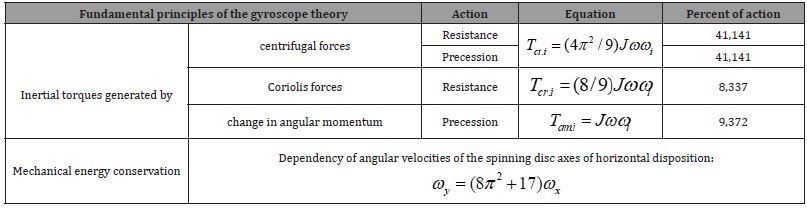
Table 1 contains the following: J is the moment of inertia of the disc; ω, ωy, and ωx are the angular velocities of spinning disc rotations about their axis oz, oy, and ox, respectively, other components are as described above.

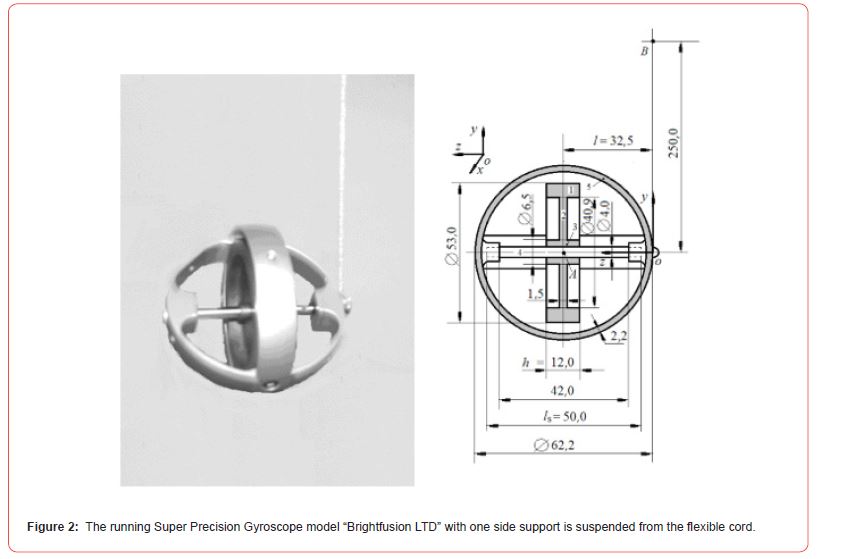
The fundamental principles of the gyroscope theory (Table 1) were used for mathematical modeling and practical tests of the gyroscope suspended from the flexible cord which was the most unsolvable problem [4, 11-13]. The action of external and inertial torques is considered and tested by the model of the Super Precision Gyroscope “Brightfusion LTD” suspended from the flexible cord that is presented in (Figure 2).

The mathematical model of motions for the gyroscope with one side free support was considered in detail, solved, and practically validated. The results of the study of the acting torques and the gyroscope motions were presented in several publications [7]. Equations of motions of the gyroscope of horizontal disposition, and suspended from the flexible cord around axes ox and oy are represented by the following final expressions:

oy (Figure 1). The rule described in Section 4 of [7] subtracts the secondary torques generated by the centrifugal forces acting about axes oy and ox.

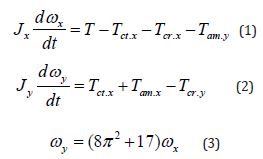
where J_x = J_y is the moment of gyroscope inertia about axis ox and oy respectively that calculated by the parallel axis theorem; ωx and ω_y is the angular velocity of precession about axis ox and oy respectively; T = Wl =Mgl is the torque generated by the gyroscope weight W about axis o_x; M is the mass; g is the gravity acceleration; l is overhang distance of the gyroscope center-mass to the free support; Tct.x is the resistance and the precession torques generated by centrifugal forces about axis ox and oy respectively (Table 1); T_cr.x and T_cr.y is the resistance torque generated by Coriolis forces about axis ox and oy respectively (Table ); T_am.x and T_am.y is the precession and resistance torque that generated by the change in the angular momentum of the spinning rotor about axis ox and oy respectively (Table 1).

The torque generated by Coriolis force of the rotating gyroscope center-mass about axes ox and oy and the torque generated by the centrifugal forces of the rotating gyroscope center-mass about axis oy are omitted because of the small values that can be neglected. Substituting defined parameters and equations of the inertial torques (Table 1) into Eqs. (1) and (2) and transformation yield the following system of differential equations:

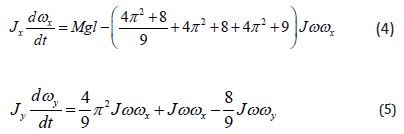
Simplifications of Eqs. (4) and (5) yields the following

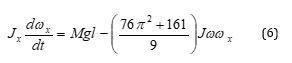
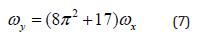
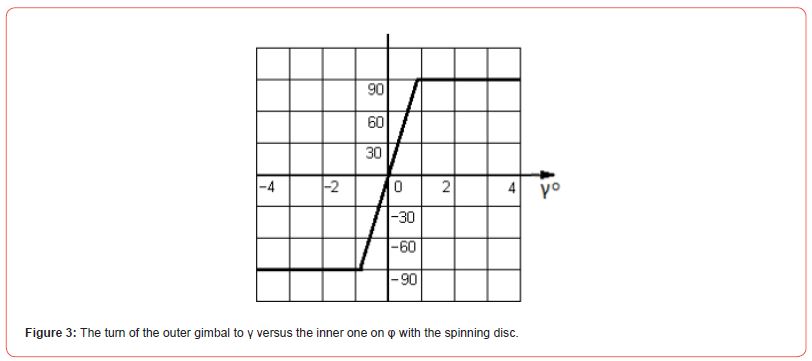
Practical tests validated Eqs. (6) and (7) with the deviation of the motion less than four percent. Equation (7) is validated by the motions of the external and internal gimbals of the laboratory gyroscope. The small tilt of the external gimbal on γ = 1,876o around axis ox yields the turn-on from φ = –90o to φ = 90o about axis oy of the internal gimbal with a spinning disc.

The rotations of the gyroscope gimbals confirm the correctness of Eqs. (6) and (7).

Figure 3 shows the change in the angular dispositions of the inner and the outer gyroscope gimbals. The theoretical and practical tests discover the nature of gyroscopic gimbals rotation which was one in the series of former unsolved gyroscopic effects.

The Industrial Revolution initiated scientists to study gyroscopic effects manifested by spinning objects. The gyroscopic effects were explained by researchers presumably and intuitively. In reality, the physics of gyroscopic effects turned out that are more sophisticated than contemplated by researchers. The physics of gyroscopic effects are described by mathematical models for the action of inertial torques on the spinning disc and its motions in a 3D coordinate system. The looped dependency of the system of gyroscopic effect is shown by the causal investigatory method of the action of the eight interrelated inertial torques. This sophisticated interrelation of the inertial forces and motions around the axes of the gyroscope is perceived with difficulty by readers. The inertial torques acting around axes are produced by four centrifugal and two Coriolis forces and the two changes in the angular momentum generated by the rotating mass of the spinning disc. The system of inertial torques and interrelated motions of the spinning disc make up the fundamental principles of the theory of gyroscopic effects based on the mechanical energy conservation law. The basic gyroscopic effects are validated by practical tests. The breakthrough theory of gyroscopic effects opens a new chapter in the dynamics of rotating objects of classical mechanics [14-16].

The theory of gyroscopic effects contains new methods for deriving mathematical models for inertial torques generated by spinning objects in engineering. Intensification of the work engineering mechanisms and machines with rotating components requires reliable decisions for computing their dynamic parameters. Numerous rotating objects movable in space still do not have engineering methods for computing dynamic parameters. The theory of gyroscopic effects contains the fundamental principles which open new directions in the dynamics of rotating objects in engineering. The method of mathematical modeling for gyroscopic effects produced by the spinning disc shows the effective solution for inertial torques that can be used in engineering for rotating objects with complex geometries.

The Kyrgyz State Technical University after I. Razzakov supported the research work for a publication that was performed as part of the employment. The author did not receive specific funding support for the article and does not have any potential conflict of interest.

The authors declare that the data supporting the findings of this study are available within the article.

No conflicts of interest.

1. G Greenhill (2015) Report on Gyroscopic Theory, Relink Books, Fallbrook, CA, USA.
2. J B Scarborough (2014) The Gyroscope Theory and Applications, Nabu Press, London.
3. V Apostolyuk (2016) Coriolis Vibratory Gyroscopes, Springer International Publishing, Switzerland.
4. WC Liang, SC Lee (2013) Vorticity, gyroscopic precession, and spin-curvature force. Physical Review D 87(4): 044024.
5. MD Aardema (2005) Analytical Dynamics, Theory and Application, Academic/Plenum Publishers, New York.
6. F Scheck (2018) Mechanics, Springer Verlag, Berlin Heidelberg.
7. R Usubamatov (2022) Theory of Gyroscope Effects for Rotating Objects, Springer, Cham, Switzerland, (2^nd).
8. R Usubamatov, D Allen (2022) Corrected inertial torques of gyroscopic effects. Advances in mathematical physics 2022: Article ID 3479736, 7 pages.
9. R Usubamatov (2022) Inertial Forces and Torques Acting on a Spinning Annulus, Hindawi. Advances in Mathematical Physics 2022: Article ID 3371936, 10 pages.
10. R Usubamatov (2022) Corrected Physics of Deactivation of Gyroscopic Inertial Torques. PriMera Scientific Engineering 1(2): 01-04.
11. JL Crassidis, FL Markley (2016) Three-axis attitude estimation using rate-integrating gyroscopes. Journal of Guidance Control, and Dynamics 39(7): 1513-1526.
12. RC Hibbeler, KB Yap (2020) Mechanics for Engineers-Statics and Dynamics, Prentice Hall, Pearson, Singapore (14^th).
13. DR Gregory (2012) Classical Mechanics, Cambridge University Press, New York.
14. FJB Cordeiro (2015) The Gyroscope, Createspace, NV, USA.
15. JR Taylor (2005) Classical Mechanics, University Science Books, California, USA.
16. Andrei D Polyanin, Alexander V Manzhirov (2007) Handbook of mathematics for engineers and scientists, Chapman & Hall/CRC Taylor & Francis Group 6000 Broken Sound Parkway NW, Suite 300 Boca Raton, FL 33487 2742.