The Acceleration of Least Squares Monte Carlo in Risk Management

The Least Squares Monte Carlo (LSMC) method was first proposed by Longstaff and Schwartz [1] to price the American option, since then it has been applied in different industries from banking [2] to energy sector [3]. In the last decade, there is an increasing demand for sophisticated risk modeling [4]. To overcome the computational complexity of those models, the proxy techniques have gain popularity in both risk management practice and research over the last decade [5]. The idea of proxy is to approximate the original model with less features to reduce the computational complexity while keeping sufficient accuracy. Among the various proxy techniques, LSMC is a state-of-the-art approach. However, the polynomial of LSMC is still too complicated in multidimensional problems. There are several works that discussed how to further improve the computational speed of LSMC. AS.Chen and PF Shen [6] studied the computational complexity of LSMC. A.R. Choudhury [7] parallelized the LSMC algorithm for American option pricing. Another method to speed up LSMC is focusing on Monte Carlo simulation itself, using techniques such as Quasi- Monte Carlo to make LSMC more efficient [8].

Solvency Capital Requirement (SCR) of Solvency II requires the computation of the economic capital, the minimum capital giving the insurance company a 99.5% survival probability over a oneyear horizon via a full probability distribution forecast [9,10].

The SCR at level α=99.5% can be computed as

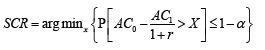
AC_t is the available capital at time t:

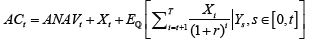
ANAV_t is the adjusted net asset value, X_t is the profit due to inforce business and Y_t is the market conditions at time t.

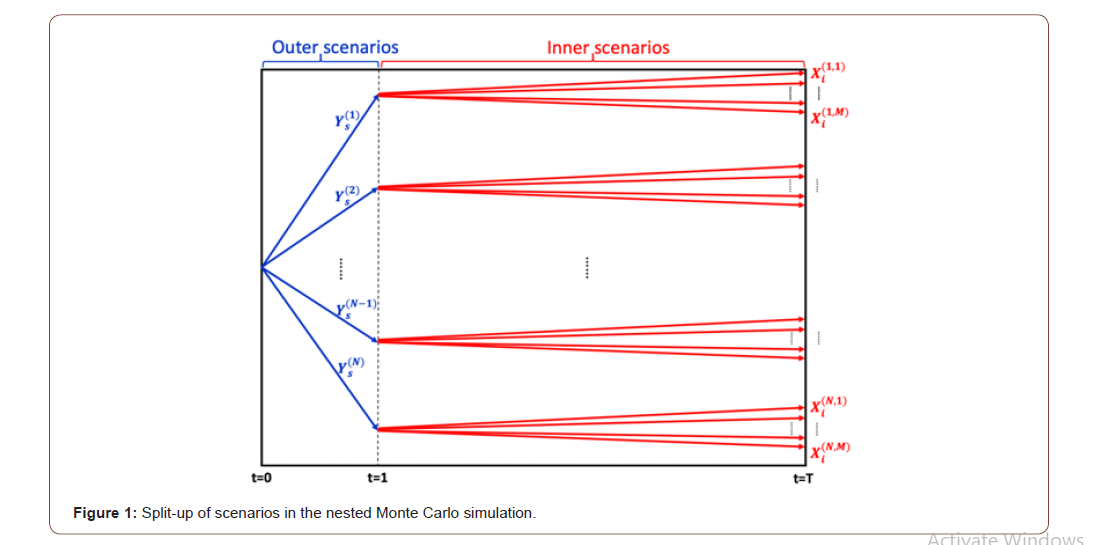
There is generally no closed-form solution, due to the very complex interactions between X and Y. Nested Monte Carlo (MC) Simulation [11] is usually need for SCR computing. To estimate AC₁, we simulate multiple paths of Y_s (outer scenarios), for each path of Ys we simulate multiple paths of Xi (inner scenarios). Then the average of present value of X_i is the estimation of E_Q. However, Nested Monte Carlo is extremely time and computer memory consuming. Imagine we have 100,000 policies, for each policy simulate 10,000 outer scenario and 1,000 inner scenarios, each scenario takes 0.001 second, then it would take 32 years to finish the simulation! (Figure 1).

A popular approach in actuarial practice to overcome the time consuming of nested Monte Carlo is using LSMC. Since

the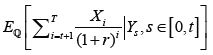 is a function of Y, it can be approximated by a polynomial:

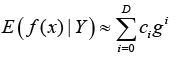
The idea is instead of using thousands of inner scenarios to find its expected present value PV(X₁) at time t=1, we train a least square polynomial regressor to approximate it with much fewer inner scenarios and for each outer scenario. The errors tend to offset one another with enough data points. This ends up with an approximator highly accurate and significantly reduced the computing time.

the 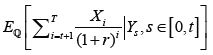is a function of Y, it can be approximated by a polynomial:

When it comes to multi-factor risks modeling approximation, the multi-dimensional polynomial would be extremely complicated. This would make the regression slow or not possible to finish within reasonable time.

To over the computational complexity of multi-risk factor LSMC, we propose distributed regression for LSMC. The idea of distributed regression is fairly simple: instead of running the regression on one computer, we distribute the regression task to multiple computers (usually using cloud computers), then average the regressed coefficients to get the final regression equation. In this way the computing time can be significantly reduced. We can mathematically prove this simple idea can actually obtain the optimal regression results [12].

There are several advantages of distributed regression: First, the computing time for the traditional least square regression is O(n³), where n is number of observations in data. While for distributed regression, it’s O(n3/m2), where m is the number of distributed computers. If we distributed the regression task to 10 computers, we could reduce to computing time to 1% of the original regression, 50 computers to 0.04%. Second, distributed regression can protect the data privacy, because very little or no communication is required when computing from distributed computers. Therefore, almost no data exchanged happened between different data platforms. If we have policy data stored in different platforms and we don’t want to share the data across, we can use distributed regression to obtain the regression coefficients from each platform then average the coefficients to get the total regression equation.

We propose the following distribute regression algorithm for LSMC:

• Step 1: Suppose the conventional LSMC requires n∙K outer scenarios. We have K worker computers and 1 master computer in our distributed system. Each worker computer generates n outer

scenarios 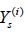nd for each outer scenario simulate 1 inner scenario X_i. In this way, we obtain n pairs of local training data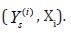

• Step 2: Each worker computer run the least squares algorithm on the local data 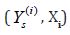to get the coefficients c_k of the polynomial to fit the function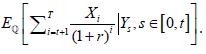

• Step 3: Each worker computer sends its fitted coefficients c_k to the master computer. The master computer averages the coefficients 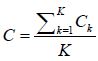and output this as the final coefficients of the fitting polynomials. There is no data communication between the computers, only the trained coefficients are sent. This protects the data privacy.

• Step 4: Scale this algorithm with more worker computers to find the optimal number of computers in terms of computing speed and cost.

There are several advantages using distributed regression to accelerate the LSMC. 1) The current parallel algorithms for LSMC require the parallel computing of the big matrix inverse, while using distributed regression we only need compute the small matrix inversion for each chunk of data. 2) When comes to multi-risk modeling, the amount of the outer scenarios would be huge that no single computer can handle it. For a N risk-factor problem, it will require 10000N outer scenarios if we simulate 10,000 outer scenarios for each risk-factor. If we use distributed regression, each computer only needs processes a smaller chunk of data assigned. 3) This divide-and-conquer type distributed learning method can also be applied to speed up other algorithms like clustering, treebased method, deep learning etc. 4) Easy to be scaled on distributed framework like Map-reduce, or Spark [13].

None.

No conflict of interest.