Stiffness of Three-Phase Concentric Composite Solids

Consider a composite with two-phase concentric inclusions uniformly distributed over the volume (Figure 1). Our goal is to evaluate the stiffness of such three-phase material given the engi neering constants of each phase. The solution is obtained by the following superposition of two-phase composite models represented in Figure 1 for spherical inclusions.

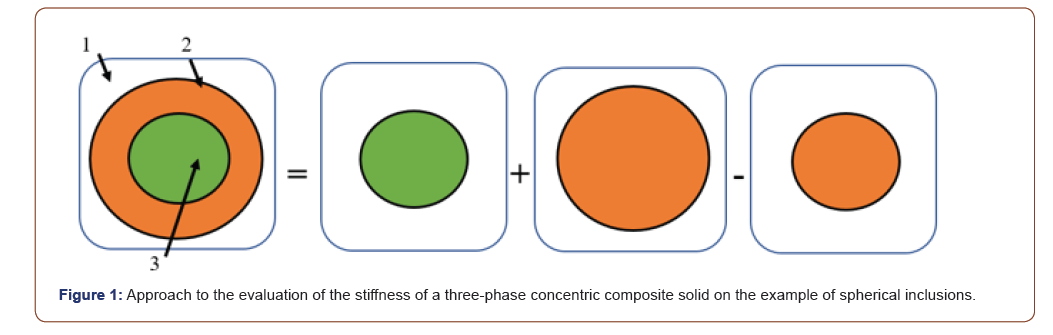
The stiffness tensor is found as the following combination of the stiffness tensors of two-phase composites:

As an example of the application of the method described above, the tensors of stiffness of two-phase materials in the right side of eqn. (1) can be evaluated by the Mori-Tanaka method using the solution by Benveniste [7]:

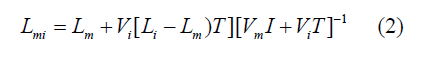
where subscripts “m” and “i” refer to the matrix and inclusions, respectively, 𝑉𝑖 and 𝑉𝑚 are the volume fractions of the inclusions and matrix, 𝑰 is the unit tensor and 𝑻 is the strain concentration tensor of dilute inclusions:

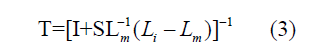
In eqn. (3), 𝑺 is the fourth order Eshelby’s tensor. In the case of spherical inclusions, explicit formulas for engineering constants are available.

Another example of solutions employing eqn. (1) can also be obtained in the case where inclusions are cylindrical and randomly oriented. The comprehensive solution can be derived using the well-known Tsai-Pagano method based on the properties of a unidirectional composite that are obtained by the Tsai-Halpin method. The solution can also be obtained by the method of Christensen and Waals [8,9]. In particular, a very simple solution is obtained if the inclusion volume fraction is below 20%. While the Poisson ratio is adequately approximated by the rule of mixtures, the modulus of elasticity of the material with 3-D randomly oriented fibers is obtained by

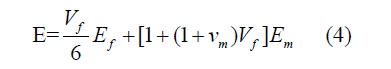
where the subscript “f” refers to the fibers, 𝐸, 𝐸𝑓 𝑎𝑛𝑑 𝐸𝑚 are the moduli of elasticity of the composite, fiber and matrix, respectively, and 𝜈𝑚 is the matrix Poisson ratio. Notably, the present equation does not account for the fiber aspect ratio; accordingly, it may not be suitable for short fibers where this ratio has a noticeable effect on the stiffness.

The examples of micromechanical methods suitable for using with the proposed two-phase superposition approach can be extended to any analytical theory, such as self-consistent, Ponte Castaneda- Willis and Kuster-Toksoz methods, etc. Numerical examples and a comparison with available solutions and experimental data will be included in an extended article.

In conclusion, the present method enables to approach the analysis of the stiffness of three-phase and, with the necessary expansion, multi-phase concentric composite solids using available micromechanical methods for two-phase composites. Such approach can significantly simplify the analysis of relevant composite materials.

None.

No conflict of interest.