State of the Art: Deterioration Models of Railway Ballasts and Subgrades. Recommendations and Applications

In recent years, rail transport has experienced a great expansion throughout the world, becoming an efficient and competitive transportation system for countries that have thousands of kilometers of tracks. In the coming decades, we contemplate that new and ambitious railway projects will be developed, and the technical difficulties in the interaction with the environment, through which the track aims to circulate and reach greater speeds, make these projects a real challenge for civil engineering. Such are the cases of the expansion of the High-Speed network in China [1] and the expected development of high-speed lines in the United States [2].

With respect to high-speed networks, the demographic and economic growth of many of the countries that have a rail network with these characteristics with optimal exploitation conditions and study experience has forced the networks to reach higher speeds to meet the demand and/or economic objectives that are required of this transportation system. The increase in speed could generate an increase in the values of the loads that are transmitted to the railway platform, since the speed is proportional to the value of the loads. This proportion is related to the effect of the weight of the nonsuspense masses of the train, since if this weight does not change but the value of the speed increases, the dynamic effects that occur in the vehicle-track interaction cause this interaction to generate a dynamic overload that increases the value of the loads to be supported by the track. In terms of railway freight transport, the future commercial expansion of several countries can lead to trains having to increase their load and/or transport capacity, either by increasing the number of cars or the axle load that is transmitted to the railway platform [3], thus considering the adaptation of this With respect to high-speed networks, the demographic and economic growth of many of the countries that have a rail network with these characteristics with optimal exploitation conditions and study experience has forced the networks to reach higher speeds to meet the demand and/or economic objectives that are required of this transportation system. The increase in speed could generate an increase in the values of the loads that are transmitted to the railway platform, since the speed is proportional to the value of the loads. This proportion is related to the effect of the weight of the nonsuspense masses of the train, since if this weight does not change but the value of the speed increases, the dynamic effects that occur in the vehicle-track interaction cause this interaction to generate a dynamic overload that increases the value of the loads to be supported by the track. In terms of railway freight transport, the future commercial expansion of several countries can lead to trains having to increase their load and/or transport capacity, either by increasing the number of cars or the axle load that is transmitted to the railway platform [3], thus considering the adaptation of this

Awareness of the economic and landscape impact generated by the design and construction of a track with these characteristics has led to an awareness of the need to assess and treat local trace materials by avoiding the massive waste of these materials, as this waste may raise consideration of the possibility of subjecting them to a treatment that improves their geomechanically behavior and makes these wastes suitable to be used in the construction of the railway platform.

The design of railway platforms has been performed, from the point of view of experience in the case of high speed, from a very conservative approach for subgrades that form the track. In the current context of economic crisis, it is necessary, both in the fields of exploitation and design, to introduce certain design criteria that ensure the cross section of the railway platform, for any type of traffic, is defined according to efficiency criteria, rationalization of these criteria and long-term sustainability

These three aspects-increased loads on the railway platform, geotechnical characterization of the materials available in the trace materials, and the efficient and sustainable design of the infrastructure- make it necessary to elaborate a new paradigm of design methodology that can include these aspects when designing a railway network with different traffic configurations, typologies of structural sections and exploitation criteria. In recent years, the continuous development of new numerical tools and more sophisticated designs has allowed integrating, in a comprehensive manner, some of these criteria that intervene in certain infrastructure projects. However, one of the least-considered criteria in this whole process is evaluating the deterioration over time of the infrastructure as a whole or of some of the materials that compose the infrastructure, since these materials can condition the overall long-term behavior throughout the useful life.

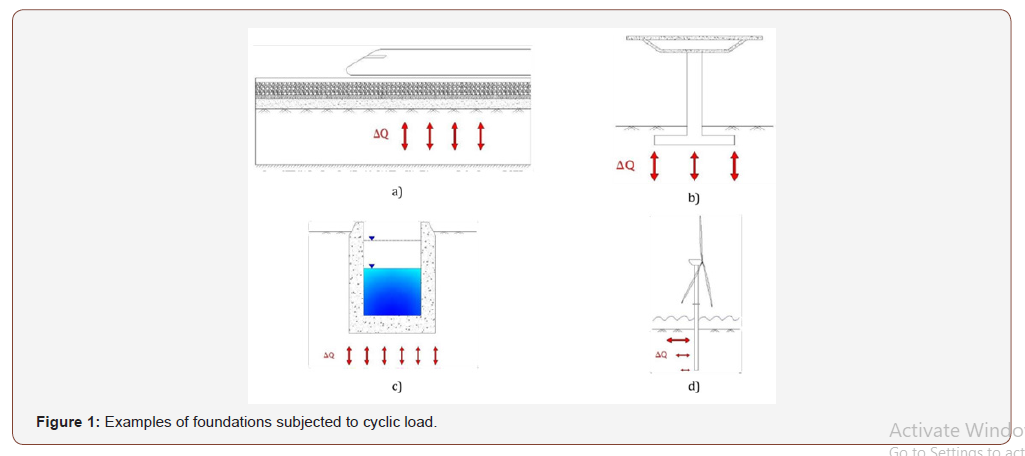
In civil engineering projects, the materials that make up a structure or a transport infrastructure are subject to different types of stresses, such as traffic loads, natural phenomena, or major forces caused by other external agents, throughout their useful life. All these stresses cause wear and the appearance of damage to the infrastructure that are usually translated into the appearance of pathologies, such as excessive deformations and the deterioration or loss of quality and properties of the materials that constitute it. In the case of transport infrastructure, the materials that make up the structural section are affected by a continuous deterioration due to their own weight, together with the high traffic loads that they receive throughout their useful life, translated into a set of cyclic loads with different frequency of application, particularly for granular materials that are more affected due to a possible lower resistance with respect to other usable materials. Along with the transport infrastructure (Figure 1(a)), the problem of deterioration in granular materials has become relevant in other scenarios such as the foundations of structures subject to cyclic loads due to dynamic or seismic loads (Figure 1(b)), the soils that support the reservoirs, water tanks and other hydraulic infrastructures due to variations in the level of these soils (Figure 1(c)), onshore and offshore structures subjected to wind and wave loads (Figure 1(d)), etc. In the field of ocean engineering, the development of new models for deterioration prediction in recent years is due to the great interest in knowing the long-term behavior of soils that can be used for foundations of offshore structures. Such models are based on those used for transport infrastructure, especially those applied to rail traffic [4]. However, even if one refers to rail traffic for the development of these models, it is precisely in this area where, in recent years, several studies have been conducted to obtain a model of more effective prediction due to the geotechnical complexity involved in the study and behavior of a railway cross section.

The purpose of this paper is to describe the state of the art relative to the development and application of the different mathematical models that allow quantification of the prediction of deterioration of granular materials in railway platforms under low cyclic load situations by reviewing the different aspects that must be considered in the characterization of the behavior of materials under long-term cyclic loading. First, a review of the concepts and parameters that intervene in the characterization of the dynamic behavior of granular materials and that may be useful for numerical or experimental studies is made, involving the application of numerous load cycles. Then, a detailed and comparative description will be made of the different analytical and numerical models developed to be applied in the prediction of the deterioration of the granular materials that form the railway platform. Finally, a series of recommendations obtained from the analysis of the described models will be presented.

In recent years, the concepts of quality and sustainability in engineering projects have been acquiring special relevance, initially due to a period of economic crisis that conditioned the best use of available natural resources and the high governmental and social pressures that demand that the designed infrastructure fulfill sustainability and guarantee criteria in terms of their duration for the next generations. In the field of transport infrastructure, the design methods have presented continuous innovation to guarantee proper functionality and service provision in future periods, conditioned possibly by greater demands of the population, higher traffic intensity and the possibility of coupling them in an intermodal system with other transport modes that could require a new conception in their design.

Within these criteria of quality and long-term sustainability, the concept of deterioration is particularly relevant. Deterioration can be defined as the wear, worsening or loss of value of a certain good due to its continuous use, exposure to certain natural agents, etc. It is also important to indicate that this deterioration may also condition the loss of certain properties of the material and its configuration over time, mainly due to its behavior model in light of these previous situations.

The study of the deterioration of a material or a system can use two different approaches: short or medium term, and that which will be produced in the long term. The first approach is usually related to problems that involve the application of larger loads but with a shorter duration (i. e. , earthquakes, impact loads, etc. ), generating large deformations in small time intervals and for which the theoretical developments and numerical tools have allowed the resolution of soil-structure interaction problems efficiently and without too many computational problems.

For problems involving long-term deterioration, these occur when the materials are subjected to low load-discharge cycles for numerous times, on the order of 105-106. In the case of transport infrastructure, this number of cycles indicates the number of axles of vehicles that are going to pass over it, an equivalent way of representing the total load to which the materials are going to be subjected. Unlike the previous approach, applying certain calculation methods is no longer viable and should be used to formulate new models, which is key for defining a numerical resolution strategy and a constitutive model capable of modeling the long-term dynamic behavior of materials.

Evolution of long-term deformation due to the number of cycles

In transport infrastructure, the design criteria and geometric tolerances play a fundamental role in the quality and functionality of the infrastructure throughout the useful life, knowing that to guarantee the latter, it is necessary to know the state of deformation with respect to the original state due to the passage of the successive vehicles over it. The knowledge of the resultant settlement resulting from the deterioration of the materials that make up the infrastructure is key when deciding the periodicity of conservation and maintenance plans, as well as the economic and technical resources necessary to return to the quality required in its design.

One of the alternatives for evaluating the deterioration state in a given infrastructure is by quantifying the deformation that can accumulate in the different materials that constitute the infrastructure during its useful life, as a consequence of the total number of load cycles applied, proportional to the number of vehicle axles that pass over it [5,6]. This deterioration in the materials can be reflected in the curves of settlement or strain evolution versus time, with the time variable represented by the number of load cycles applied in the useful life.

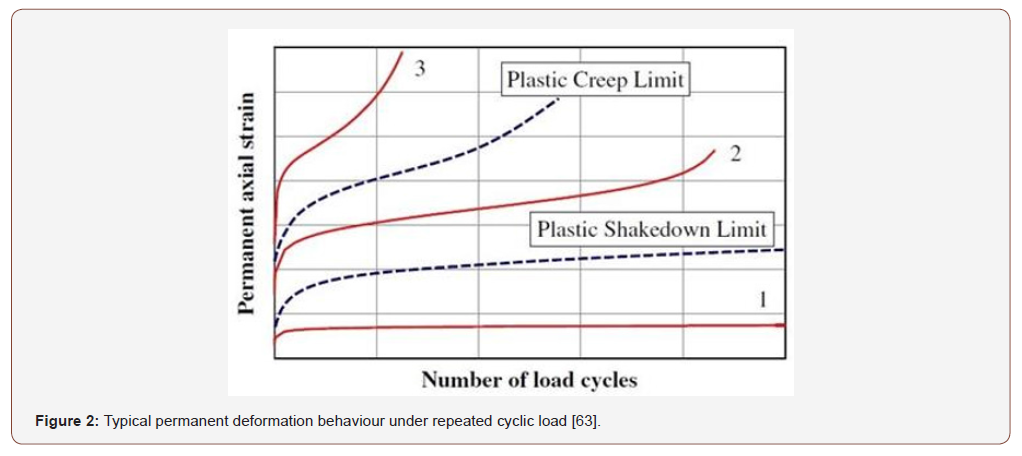
In principle, studies that evaluate the deterioration were of greater interest in the field of roads, since they were oriented for the sizing of pavements and cross sections. [7] differentiated, by conducting tests, three types of behavior in granular materials when these were subjected to numerous load cycles. Such behavior can be seen in Figure 2, separated by the plastic shakedown and creep limits [8]:

• Plastic Shakedown (Line 1): The response of the soil is completely resilient, and there is no accumulated strain for high load cycles, whose ratio decreases rapidly until reaching the state of equilibrium and, therefore, does not reach the failure.

• Plastic creep (Line 2): The response is not completely resilient, but there are tolerable permanent strains that can reach the failure after a high number of load cycles. The strain ratio can be of constant or decreasing growth.

• Incremental collapse (Line 3): Permanent reachable strain is not desirable, and the ratio increases rapidly and is able to reach the failure with the application of few load cycles./P>

Figure 2 shows how the continuous application of loads leads to the generation of a succession of strain “micro-increments” that accumulate over time and can reach an excessive plastic deformation that can become the primary concern of designers and technicians, seeing the possibility that the materials reach different service limit states. Depending on the properties of the material to be studied (morphological properties, strength, etc.), its deformational response to the application of successive loads will be similar to those shown.

The satisfactory contribution made by the knowledge of the deterioration in roads and other similar infrastructure meant that, little by little, it was being applied and used for materials of different rheology and locatable in other fields, such as those found in railway cross sections. The interest to be applicable in this field was motivated by the detection of problems caused on railway tracks due to the appearance of pathologies related to the appearance of plastic deformations, which could lead to the failure of the material or of the whole of the infrastructure if not properly controlled [6,9]. The failure of the railway cross section, caused by excessive permanent strain, may be because the behavior of a single material is not entirely safe for the application of a certain number of loads, resulting in affecting the entire section due to the joint interaction of all the materials.

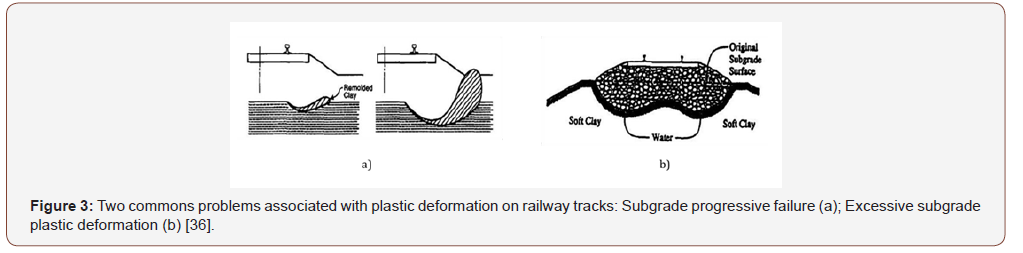
Some of the most common failures detected are the subgrade progressive shear failure (see Figure 3(a)), associated mainly with fine-grained soils containing clays that usually configure the embankment or foundation of the track and that generate a plasticization and a horizontal and vertical mobilization of the soil (ORE, 1970); and the excessive subgrade plastic deformation (see Figure 3(b)), associated with the combination of the joint action of the self-weight by consolidation and the application of the railway load, which generates large deformations in areas where the greatest stresses are applied and, therefore, differential settlements in the track and subsidence of the ballast and sub-ballast in the lower layers [10].

Models and parameters that characterize the behavior of granular materials under cyclic loads

Since there is evidence that soil or granular media show a different behavior in a saturated, semi saturated or dry state, the complexity in the study of their behavior increases when considering their response to dynamic stresses [11]. Throughout the years, the realization of infrastructure and other types of construction on different granular media, which could be affected by dynamic demands, led to the performance of investigations and studies to analyze and characterize the mechanical behavior of soils before different physical states and loads [12], particularly if these physical states and loads were cyclic. These studies allowed the definition of behavior models based on the definition of constitutive equations of a complex nature, based on those used by models that considered the elastoplastic behavior of materials for monotonous loads and that could easily be implemented in the numerical tools used until that moment.

In general, a succession of applications of isotropic loads with subsequent discharge generates a progressive compaction of the particles that make up the medium, causing the soil to experience two types of deformations in each cycle, one elastic 𝜀𝑒 ,and the other plastic 𝜀𝑝 (see Figure 4), the latter being the irreversible deformation that accumulates as more load cycles are applied. If this process is repeated over time, we can say that the soil is being subjected to a state of cyclic loading, generating these two types of deformations in different proportions according to the behavior model of the material itself.

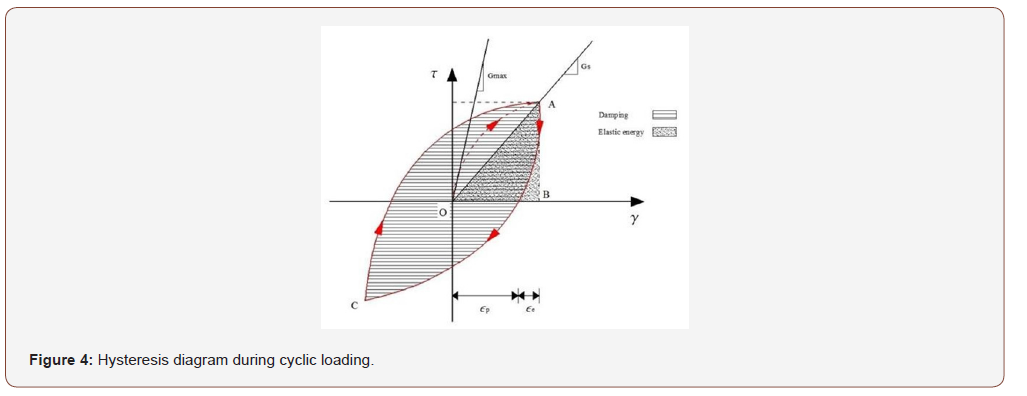
The appearance of plastic strains during the successive charge-discharge cycles causes the stress- strain diagram to acquire the hysterical form shown in Figure 4, with the shear stress in the ordinate and the shear strain in the abscissa. In the diagram, several trajectories can be observed: a “noval” path (OA) [11] of application of the load, where the material offers a nonlinear response; and an unloading path (AB) in which plastic strains begin to occur with a zero stress. One path corresponds to a reverse stress taking a maximum value in C, symmetrical with A; and a new loading that would lead back to point A and then to a new different cycle. The area enclosed by the diagram indicates the damping capacity of the system, that is, its capacity to dissipate energy in the loading-unloading processes, whether damping of a viscous or hysterical type.

The complexity of combining the phenomenon of elastoplasticity with the dynamic behavior of soils under cyclic loads, especially for large deformations (γ) of the order of 10-4 to 10-2, favored the development of equivalent linear models into which it was intended to incorporate the nonlinear behavior of the material through a modulus of secant strain 𝐺𝑠 (see Figure 4), in a way similar to what would be assumed to be a linear-type behavior. In addition, the use of this type of model allows the consideration of the effect where an increase of the deformation would lead to a decrease in the rigidity and to the increase of the damping capacity of the material [13].

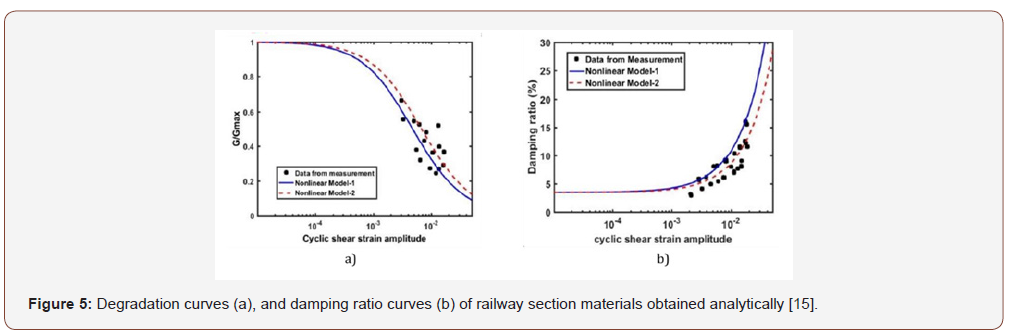
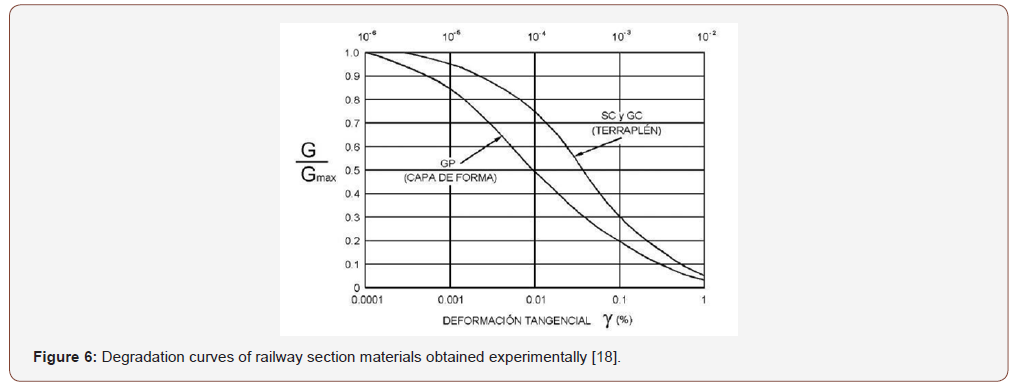
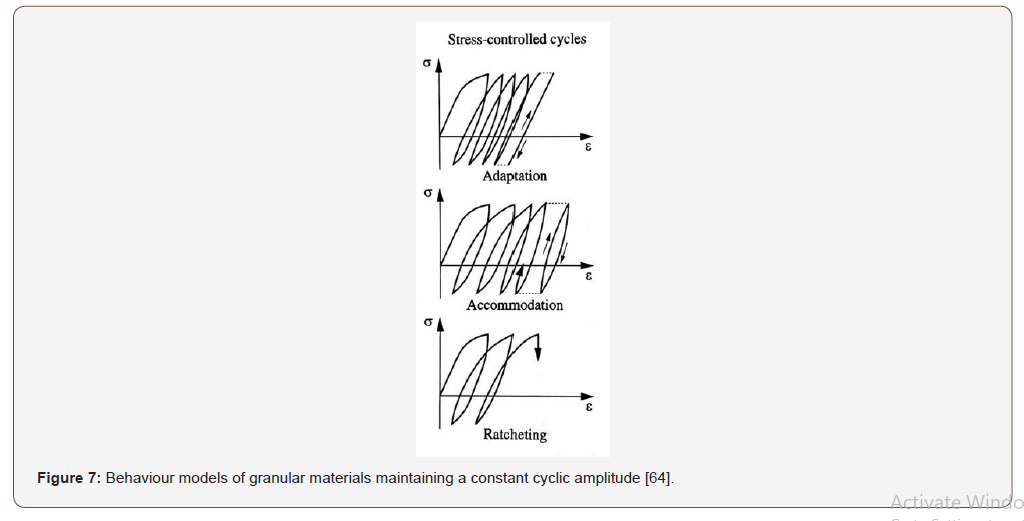
For the definition of this type of model, two parameters were necessary [14,15]: (i) the elastic properties of the material for small deformations, obtained by propagation tests of waves of S cutting, which induces cyclic shear stresses, and (ii) the functions that govern material degradation and increased damping with increased strain. With respect to the functions that control the degradation and damping of the materials, different alternatives have been proposed to characterize the deterioration of material characteristics. On the one hand, different researchers have defined empirical analytical relationships, calibrated with experimental studies, that consider the effect of soil type, its strength, etc. Some of the most widely used relationships are those proposed by [16], which have had satisfactory applications for different problems and numerical studies [14,17] (see Figure 5). Otherwise, resonant column testing with the different materials also allows obtaining the degradation curves [18] (see Figure 6) to introduce them in a numerical tool that models the deterioration with the application of the successive loads [19,20]. When studying the cyclic behavior of a granular material, it is important to visualize the different phenomena of plasticity associated with each individual loading process. If we subject the granular material to a constant load amplitude, depending on its strength and morphological properties, some of the cyclic behaviors represented in Figure 7 will occur (Cambou and Hicher, 2010): a phenomenon of “adaptation” occurs, in which part of the process of successive cycles where there is dissipation of energy and which is converging to closed cycles, not dissipative, where the behavior is purely resilient. The phenomenon of “accommodation” corresponds to an open cycle with dissipation of energy and an accumulated irreversible deformation that evolves to a stabilized cycle. The “ratcheting” phenomenon corresponds to a set of open cycles with accumulated irreversible deformations and which maintains the same shape. Different researchers have shown that the reach of the elastic state by the granular materials is closely linked to the value with the “resilient module”, an essential parameter for the study of their behavior under a state of cyclic loads, as their value characterizes the elastic stiffness in each individual cycle of load. [21] quantified the value of the resilient modulus 𝑀𝑟 for triaxial tests with constant cyclic loading as the ratio of the cyclic deviator stress in each load cycle with the recoverable (resilient) strain in the axial direction that maintains a constant confining pressure:

where 𝜎_𝑑 is the cyclic deviator stress, 𝜎_{1 and 𝜎3 are the first and third principal stresses in each load cycle, and 𝜀𝑟 is the resilient strain in the direction of the axial stress (𝜎1) with a constant confining pressure (𝜎3).}

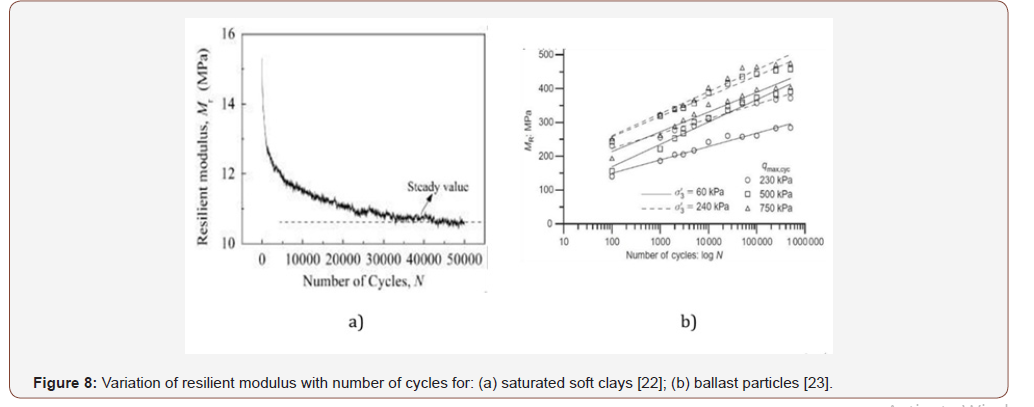
Depending on the physical and mechanical characteristics of soils, the variation of the resilient module with respect to the number of total cycles applied will be different, possibly linear or nonlinear. [22], through cyclic triaxial tests with saturated soft clays, showed that the variation of 𝑀𝑟 was decreasing, with a higher ratio for the first 1000 cycles, and that after these cycles, it tended to a lower variation towards quasi-constant values (see Figure 8(a)), probably due to an increase in pore pressure. Conversely, other researchers [23,24] could verify that, in the case of induced compaction of larger particles (i. e., ballast), the variation of Mr is usually increased if the number of load cycles applied increases (see Figure 8(b)). To better understand the physical meaning of the resilient module and its best application to study the cyclic behavior of granular materials, different researchers began to identify factors to which this parameter could be sensitive [25]. For example, with the increase in the cyclic deviator stress 𝜎𝑑, the resilient modulus could tend toward increasing or decreasing variations [26-28], or the moisture content could affect its tendency toward variation [29,30]. All this research was represented in mathematical expressions that could reflect such tendencies for each material studied. [31] surmised, from previous studies, that the value of 𝑀𝑟 was significantly influenced by three factors: (i) initial state of tension and load conditions, (ii) type of soil and (iii) physical state of the soil (i. e. , wet, dry density, etc. ), which were introduced implicitly in some of the following empirical models of reference:

• Bilineal model [32]:

where 𝜎_𝑑𝑖 is the deviator stress for which the slope of 𝑀𝑟 changes with respect to 𝜎𝑑; 𝐾₁, 𝐾₂, 𝐾₃, and 𝐾₄ are parameters dependent on the type and physical state of the soil.

• Power model [33]:

where 𝑘 y and 𝑛 are parameters dependent on the type and physical state of the soil.

• Semilog [34]:

• Hyperbolic model [28]:

• Octahedral model [35]:

where 𝑚 is a parameter dependent on the type and physical state of the soil, and 𝜎_𝑜𝑐𝑡 and 𝜏_𝑜𝑐𝑡 are the normal and tangential octahedral stresses.

In Figure 9, some analytical representations of the previous models are shown, with observations of the existing differences in choosing each of them. The forms of the previous expressions can also be used as a reference since, depending on the experimental results obtained for each material, the form of one or the other expression will be advisable.

In the previous section, a review of the concept and importance of deterioration has been performed for the materials that form a transport infrastructure, since the observation of the material’s behavior throughout its life is essential for its correct functionality. For a given material, such deterioration can be observed through its strain number of axles applied to the curve or through the tendency of variation of its geomechanical properties.

Most authors considered the joint study of the evolution of the strain and the value of the resilient module essential with respect to the number of cycles applied, which is the first parameter most commonly used for this study. Its choice may be due to greater interest and because of the available tools capable of quantifying, in a simple or more complex way, its value with respect to the type of material and the number of cycles applied.

The infrastructure must be designed according to safety and efficiency thresholds. Since the end of the 1970s, different authors began to consider that any material, in a certain situation, could not exceed allowable values of strain in certain transport infrastructure so as not to compromise its functionality and the safety of the users. Therefore, the criterion that had to be considered for the design and stability of the soils that form the infrastructure or that serve as a foundation for any type of structure is the following:

where 𝜀𝑝 is the accumulated plastic strain, and 𝜀𝑝𝑎 is the allowable plastic strain for a design period ([36]. Since then, the value of 𝜀𝑝 has been quantified in different ways for different types of soils and in different sets of infrastructures, since the heterogeneity of the materials present in the traces of the same materials requires knowing the behavior of all of them for the quantity of applied axles.

The quantification of the accumulated plastic strain has been evolving according to the tools present in each situation, with the use of mathematical models most common in obtaining, a priori, a value of strain for a certain number of axles applied. Literature today classifies the mathematical models used in these problems into two major groups: the empirical-experimental and theoretical methods. In addition, recent developments in numerical tools and calculation strategies have enabled a possible and advantageous integration of these methods into a single method that encompasses them.

Next, the different prediction models of the deterioration of granular materials collected in the state of the art, expressed in Tables 1, 2 and 3 and applied mostly in the railway field, will be briefly described.

Empirical-experimental cumulative models

Mathematical developments and the application of analytical expressions that could predict soil deterioration began with greater interest in roads [5] and, since then, have continued to develop with more interest in the current era due to the interest in build new infrastructure and buildings that are located in soils that experience unstable behavior in the medium to long term [4,8].

Initially, these expressions were too general and not applicable to specific geotechnical problems present in certain types of infrastructure. This lack of applicability motivated different engineers and researchers from different places to deepen the study and search for expressions that, with the support of experimental tests, allowed them to predict the behavior of materials in different environments, load conditions and types of infrastructure. The main advantage of this type of model is the direct application in problems without the need to carry out excessive calculations, but due to their great empirical load, it is possible that they may not obtain very precise results compared to those observed in experimental tests or real cases studies, thus, before its application, it is essential to know if the values of the different variables involved in the formulation are available.

Table 1:Empirical-experimental models for prediction of deterioration.

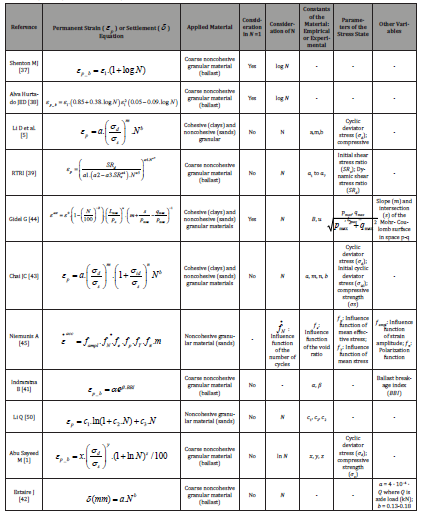
In the field of railway engineering, based on studies in roads, engineers and researchers have reached informed empirical analytical models in observing the behavior of granular materials constituting the railway platform by considering the different physical characteristics of the materials and design parameters. Table 1 shows some of the most common prediction models applied to railway platforms. From these models, ordered by date of publication, the different criteria considered in each expression can be observed in terms of material characteristics, the stress state of the materials (either by strength or under loading conditions) or other variables not related to the previous variables. In the table, one can also see the different applicability of each of the expressions for the different materials that make up the railway platform.

With respect to ballast, the expressions of [37,38] are easy to apply since they do not depend on the soil characteristics and stress state, instead depending only on the number of cycles applied. The purely empirical character and the absence of characteristic parameters of the soil, together with the age of the expressions, can generate uncertainty when using them, and these expressions should be used to obtain a first reference deformation that can serve to enhance other expressions. More elaborate expressions include those published by [39,40], which already take into consideration different constants of the material and values of the stress state in the ballast. With respect to the second reference deformation, the values of the constants are tabulated according to the type of ballast used in the track, which facilitates its application. Other expressions, such as those of [41,42], consider other variables such as the breakage index of the ballast particles, the type of infrastructure, the circulation speed and the load per axle applied to the track.

If we refer to fine-grained soils used for the foundation or embankment of the railway platform, we have a greater variety of formulas of different complexity according to the number of variables to be disposed. [5] developed, from tests in different track types, an expression to predict deterioration in fine-grained soils that has been widely used and validated by different studies developed on railway tracks in the United States and whose constants can be found in tables and other publications. [43] proposed an improvement of the previous expression of [5] considering the influence of the initial deviator stress. The other expressions shown, such as by [44], are more complex than the other two previous expressions, either because they require more complex stress parameters or because an additional calibration is required according to the type and behavior of the soil to be used. Among the remaining expressions, we can highlight the high-cycle accumulation model (HCA) achieved by [45], a more complex expression obtained experimentally and based on the rate of variation of the strain with respect to time, defined as a product of six functions whose development can be found in detail in [46-47].

The above expressions do not consider the degradation of the mechanical characteristics of materials with the application of each cycle, something that is seen in section 2.2. It is important to quantify the behavior of these mechanical characteristics of materials under continuous dynamic loads and examine the extent of the deterioration. Currently, the need to understand and improve the knowledge of the deterioration of granular materials in certain infrastructure means that some of the previous expressions are continuously developing so that they can consider new factors that influence such predictions. Recently, [48] considered introducing the effect that the variation of matric suction would have on the deterioration of unsaturated granular soils in a combined equation between the expressions of [45,49], arriving at numerical and experimental results that have shown that an increase in the value of the matric suction would lead to a reduction of the accumulated strain under cyclic load states.

Constitutive models

Most of the expressions described in Table 1 were proposed to predict the cumulative axial strain assuming a constant cyclic tension throughout the process. These expressions, in addition to not considering the degradation of the material, do not consider the redistribution of stresses in the materials as a consequence of the accumulated strain. For more complex and boundary-value problems, there was a need to determine the distribution of stress through the use of constitutive models before predicting cumulative or residual deformation [50], leading to the alternative of using constitutive or “theoretical” models for the resolution of problems involving small load amplitudes with a high number of cycles.

Unlike empirical models, based on direct application equations, the so-called theoretical models are based on physical laws or the definition of constitutive laws that make use (or not) of concepts belonging to the theory of elasticity or plasticity. In addition to the models commonly used in solving geotechnical problems (i.e., Mohr-Coulomb, Drucker-Pager, Cam-Clay, etc.), different authors have developed constitutive models that seek to adapt to the search for these types of solutions, reaching values more precise than those that would be obtained with only the application of an empirical- experimental equation. Table 2 summarizes some of these theoretical models, whose application has obtained acceptable results in comparison to those obtained through experimental tests. Some of the theoretical models initiate from the concepts of the classic theories of plasticity to formulate one or several constitutive equations.

[51] formulated an expression that quantifies the accumulated plastic strain according to two mechanisms of deformation in solid particles, considering the history of load and changes of response in the material through the use of theory of plasticity laws. The differential equation, shown in Table 2, is characterized by its consistency, since it avoids introducing empirical concepts and laws in its set of parameters and equations. Its application is limited to two-dimensional or axisymmetric problems under static load conditions and without vehicle–track interactions.

Table 2:Constitutive models developed for problems of granular materials subjected to cyclic loads.

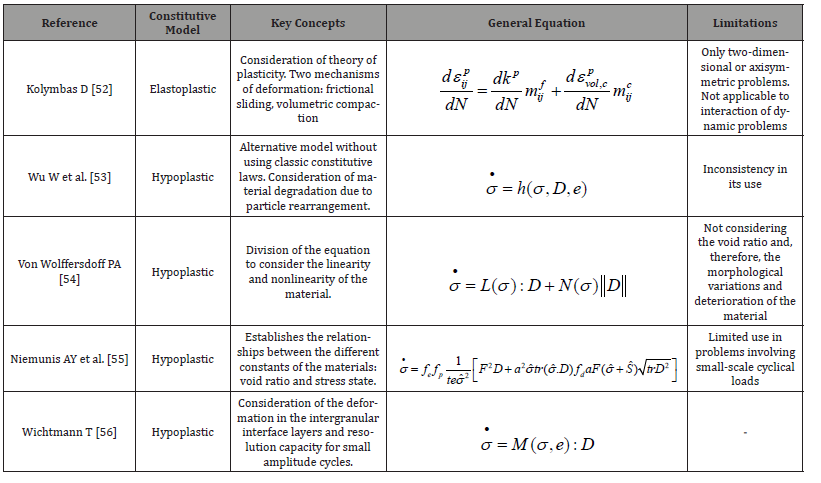
[52] formulated the “hypoplastic” model, a model alternative to classic models by not using fundamentals of the theory of plasticity and using a unique equation derived from empirical studies with trial and error, in which degradation of the material is considered through the rearrangement of the solid skeleton. Later, [53] proposed correcting the deficiencies of the equation by considering its decomposition into two parts: one that considered the linear behavior of the material and another that considered the nonlinearity, reaching the expression shown in Table 2. Finally, [54] established the relationships between the different constants of the material, with the void ratio and the stress state being the two main factors considered. This model was improved so that it could be applied to problems with cyclic loads of small amplitude by introducing a new variable, the “intergranular deformation”, which could consider the history of charges [45,55].

The application of these constitutive models can use the finite element method, as has been implemented in recent years. The main advantage that would lead to its use in a deterioration prediction problem is its possible greater precision in calculating the plastic strains generated in each load cycle. However, its main disadvantage lies in the excessive numerical errors that could be generated for a calculation involving a large number of load cycles [56,57].

Mixed or combined models

To solve the problems that can cause the use of the finite element method when performing a calculation involving high load-unload cycles, a work methodology was proposed that allowed taking advantage of each of the two methods above to obtain a more accurate prediction of the solution to the problem in question. This methodology consisted of the combination of both methods in the same calculation process [45], adopting for each model the terms of the “implicit” method with conventional numerical calculations to evaluate the strain amplitude and the “explicit “ method to study the accumulation strain for high values of 𝑁.

In the “implicit” method, each cycle is calculated by means of small increments in the finite element, being able to use a constitutive model of the material with a case of pseudo-static or dynamic loading. Different authors differ in the number of cycles that are appropriate to use in the finite element method without having an accumulation of errors that could compromise the resolution. [56] clarifies that it would be advisable that this method does not exceed 𝑁 < 50, and [57] conclude that 3~4 cycles are appropriate each time the method is applied efficiently. With respect to the “explicit” method, this requires the use of a prediction equation that allows the introduction of a certain number of load cycles 𝑁 into the equation to evaluate the strain that would be generated for such a number of cycles, that is, as a consequence of the application of all these cycles. This approach could be implemented by using some of the expressions seen in section 3.1, which would introduce the initial values of the stress state, obtained by the implicit method, and the parameters corresponding to the type of soil together with 𝑁 number of cycles.

Finally, Figure 10 shows a calculation method that allows the combination of the advantages of both methods in an integrated manner. After the application of the “explicit” step, the characteristic parameters of the soil along with the distribution of stresses and deformations in the elements should be updated through the “implicit” model using control cycles to control the numerical error caused by each of the calculation steps that are carried out.

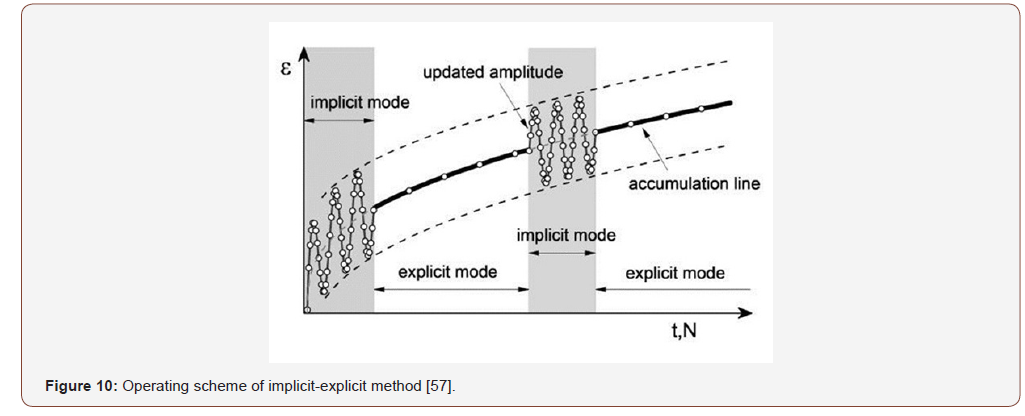
The application of this methodology is still limited because the methodology requires a thorough study of the different constitutive models in the literature, and depending on the type of problem, a calculation strategy will require a greater or lesser complexity depending on the characteristics of the materials, loading conditions and results to be obtained. The support that experimental tests or already existing results can provide should not be overlooked when obtaining an adequate calibration of the possible parameters required for the “explicit” method, as well as being able to corroborate the correct functioning of the numerical model. For example, the work of the “Institute of Foundation Engineering and Soil Mechanics” of Ruhr-University Bochum, where [45,46] defined the basic principles of application of this methodology in the modeling of problems that will involve the evolution of the settlement in different types of foundations on the long-term in noncohesive soils, led to soil-structure interaction problems with geometries and more complex conditions [58,59].

Table 3:Examples of numerical models with “implicit-explicit” method applied to railway platforms.

Relative to railway platforms, some numerical models have been developed that seek to obtain the deterioration curve of the materials that form the platform. Table 3 shows some of the more recent models. Although all of them model the complete railway platform, each one of the models analyzes the deterioration in a single material, ballast or soil that forms the embankment or subgrade. The analysis of a single material can be due to the numerical complexity of implementing the constitutive model and the prediction equation for each of the materials. The rest of the characteristics studied are related to this first characteristic. In the first place, all the models, except the one proposed by [60], consider the degradation of the studied material in question through the implementation of a constitutive model or equation that considers such an effect. With respect to the dimensions of the model, the same previous division is again present; the dimension of the model is essential to obtain an accurate resolution and without involving high calculation times. When implementing a constitutive model, different authors initially recommend the realization of two- dimensional models to observe the sensitivity that the adoption of certain parameters and the interaction of the different elements of the model would imply. This two-dimensionality of the model can be seen in [57,61], who implement a hypoplastic model that requires an update and control of the tenso-deformational parameters in each calculation step, while [62-66] implement a constitutive equation in each “implicit-explicit” transition with a criterion of convergence of a certain requirement.

Application recommendations

The information contained in Tables 1-3 helps to quantify the accumulated strain in the materials that form the railway platform. Therefore, depending on the calculation tools that are available, as well as the available data about the materials under analysis, a model can be selected to perform the deformation calculations.

The empirical-experimental models are easy to apply, but it is important to note that, depending on the material to be studied and the availability of the values of the implicit parameters of their characteristics and their tensional state, it is recommended to also use another expression. In addition, the high empirical content may lead to less accurate results than those observed in other situations.

Theoretical models require the definition of constitutive relationships for materials that can be implemented in current numerical tools, such as the finite element method, which guarantees accurate results if the model is used correctly. However, the designer must be aware of the problems associated with a calculation involving a high number of loading-unloading cycles, since this calculation may require a high computational cost and, as a consequence, produce a high accumulation of errors in the process. Some authors have recommended that this process should not exceed 50 cycles.

Finally, the advantage of using the combined method has been explained, since it seeks to solve the limitations of the two previous models. Its application is still in the development phase, having only been applied to two-dimensional models and for a single material, and further study should continue.

An updated state of the art with respect to the modeling of longterm deterioration in granular materials and their application to railway platform revision has been offered in this article. From this article, the following conclusions can be drawn.

• The deterioration can be defined with the capacity of loss of the mechanical properties of the granular material in the short or long term, depending on its response to the type of action to which it is subjected. This factor must also be considered as an additional design parameter to avoid reaching limit states that compromise the safety and functionality of the infrastructure.

• The variation in time of the resilient module 𝑀𝑟 with the application of the successive load cycles can be essential when characterizing the dynamic behavior of the materials. This variation will be different depending on the type of soil, its physical conditions and the type of load to which it will be subjected.

• Different models have been detected to quantify the accumulated plastic strain due to the high number of cyclic loads. These models have been grouped into three types according to the nature of the formulation used: empirical, theoretical and combined models.

• The analytical models of deterioration prediction are useful when calculating, as a first approximation, the strains that occur in the infrastructure, but the use of these models must be in accordance with the case to be studied and with the available data of the characteristics of the material and its stress state.

• The use of theoretical models that require the definition of constitutive laws for materials offers more accurate results than empirical expressions, but these theoretical models should be used with consideration of the possible computational problems that can occur during the calculation process.

• To solve the limitations of the two previous models, the combination of both is proposed through the combined models. Its current use is scarce and should continue to be developed for future problems involving geometries and more complex loading conditions.

• Three tables have been developed that can serve as a guide for designers and technicians of railway infrastructure so that, depending on the available data, different models can be selected to quantify the deformation accumulated in the track.

None.

No conflict of interest.

1. Abu Sayeed M, Shahin MA (2016) Three-dimensional numerical modelling of ballasted railway track foundations for high-speed trains with special reference to critical speed. J Transp Geotech 6: 55-65.
2. Fort L, Fort C (2016) España y la red de alta velocidad en Estados Unidos. Revista de Obras Públicas 3580: 36-53.
3. Li D, Hyslip J, Sussmann T, Chrismer S (2016a) Railway Geotechnics. CRC Press/Taylor & Francis Group, Boca Raton, FL, USA, pp. 35-69.
4. Ren XW, Xu Q, Teng J, Zhao N, Lv L (2018) A novel model for the cumulative plastic strain of soft marine clay under long-term low cyclic loads. J Ocean Eng 149: 194-204.
5. Li D, Selig T (1996) Cumulative plastic deformation for fine-grained subgrade soils. J Geotech Geoenviron Eng 122(12): 1006.
6. Li D, Hyslip J, Sussmann T, Chrismer S (2016c) Chapter 5: Design. Railway Geotechnics. CRC Press/Taylor & Francis Group, Boca Raton, FL, USA, pp. 197-264.
7. Werkmeister S, Dawson A, Wellner F (2005) Permanent deformation behavior of granular materials. Road Materials & Pavement Design 6(1): 31-51.
8. Wang J, Ling X, Li Q, Zhang F, Li Y (2018) Accumulated permanent strain and critical dynamic stress of frozen silty clay under cyclic loading. J Cold Reg Sci Techno 153: 130-143.
9. Selig ET, Waters JW (1994) Track geotechnology and substructure management. Thomas Telford Ltd, London, England.
10. Sánchez M, Wang D, Briaud JL, Douglas C (2014) Typical geomechanical problems associated with railroads on shrink-swell soils. J Transp Geotech 1: 257-274.
11. Lorente de No C, Soriano Peña A (1981) Cimentaciones sometidas an efectos diná In Jiménez Salas JA, Geotecnia y Cimientos III, Rueda, Madrid, Spain, pp. 751-863.
12. Luong MP (1980) Stress-strain aspects of cohesionless soils under cyclic and trasient loading. Int Symp On Soils under Cyclic and Transient Loading, Swansea, pp. 353-376.
13. Hardin BO, Drnevich VP (1972) Shear modulus and damping in soils: measurement and parameter effects. J Soil Mech Found Div 98(6): 603-624.
14. Alves Costa P, Calçada R, Cardoso AS, Bodare A (2010) Influence of soil non-linearity on the dynamic response of high-speed railway tracks. J Soil Dynam Earthquake Eng 30(4): 221-235.
15. Shih JY, Thompson DJ, Zervos A (2017) The influence of soil nonlinear properties on the track/ground vibration induced by trains running on soft ground. J Transp Geotech 11: 1-16.
16. Ishibashi I, Zhang X (1993) Unified dynamic shear moduli and damping ratio of sand and clay. Soil Found 33(1): 182-191.
17. Naeini M, Akhtarpour A (2018) Numerical analysis of seismic stability of a high centerline tailings dam. J Soil Dynam Earthquake Eng 107: 179-194.
18. Centro De Estudios y Experimentación de Obras Públicas (CEDEX) (2011) Análisis De los resultados de los ensayos de laboratorio realizados con muestras de las capas de asiento de lssos modelos realizados con muestras de las capas de asiento de los modelos físico de vía an escala real construidos en el CEDEX. Laboratorio de Geotecnia del CEDEX, Madrid, Spain.
19. Muñoz Cardador J (2011) Numerical modeling of the railway, static calculation. Master's Thesis, University of Castilla-La Mancha, Ciudad Real, Spain.
20. Gallego I, Muñoz J, Sanchez Cambronero S, Rivas A (2013) Recommendations for Numerical Rail Substructure. Modeling Considering Nonlinear Elastic Behavior. J Transp Eng 139: 8.
21. Seed HB, Chan CK, Lee CE (1962) Resilience characteristics of subgrade soils and their relation to fatigue failures. Int Proceedings of international conference on structural design of Asphalt Pavements, Ann Arbor, MI, pp. 611-636.
22. Guo L, Wang J, Cai Y, Liu H, Gao Y, Sun H (2013) Undrained deformation behavior of saturated soft clay under long-term cyclic loading. J Soil Dynam Earthq. Eng 50: 94-107.
23. Lackenby J, Indraratna B, Mc Dowell G, Christie D (2007) Effect of confining pressure on ballast degradation and deformation under cyclic triaxial loading. Geotechnique 57(6): 527-536.
24. Ng C, Zhou C (2014) Cyclic behaviour of an unsaturated silt at various suctions and temperatures. Geotechnique 64(9): 709-720.
25. Lekarp F, Isacsson U, Dawson A (2000) State of the Art. I: Resilient Response of Unbound Aggregates. J Transp Eng 126(1): 66.
26. Hicks RG, Monismith CL (1971) Factors influencing the resilient response of granular materials. High Res Rec 345: 15-31.
27. Brown S, Lashine A, Hyde A (1975) Repeated load triaxial testing of a silty clay. Geotechnique, 25(1): 95-114.
28. Drumm E, Boateng Poku Y, Johnson Pierce T (1990) Estimation of subgrade resilient modulus from standard tests. J Geotech Eng, pp. 14.
29. Myung SJ, Wayne Lee K, Kovac WD (1994) Seasonal Variation of Resilient Modulus of Subgrade Soils. J Transp Eng 120(4): 603.
30. Trinh VN, Tang AM, Cui YJ, Dupla JC, Canou J, et al. (2012) Mechanical characterisation of the fouled ballast in ancient railway track substructure by large-scale triaxial tests. Soils and Foundations 52(3): 511-523.
31. Li D, Hyslip J, Sussmann T, Chrismer S (2016b) Chapter 4: Mechanics. Railway Geotechnics. CRC Press/Taylor & Francis Group, Boca Raton, FL, USA, pp. 127-195.
32. Thompson MR, Robnett QL (1979) Resilient properties of subgrade soils. J Transp Eng ASCE 105(1): 71-89.
33. Moossazadeh J, Witczak MW (1981) Prediction of subgrade moduli for soil that exhibits nonlinear behavior. Transportation Research Record 810: 9-17.
34. Fredlund DG, Bergan AT, Wong PK (1977) Relation between resilient modulus and stress conditions for cohesive subgrade soils. Transportation Research Record 642: 73-81.
35. Shakel B (1973) Repeated loading of soils-A review. Australian Road Research 5(3): 22-49.
36. Li D, Selig ET (1998) Method for railroad track foundation design I: Development. J Geotech Geoenviron Eng 124(4): 316.
37. Shenton MJ (1975) Deformation of railway ballast under repeated loading conditions. Proceedings of the Symposium on Railroad Track Mechanics, Princton University, pp. 387-404.
38. Alva Hurtado JED (1980). A methodology to predict the elastic and inelastic behavior of railroad ballast. PhD Thesis, University of Massachusetts, Amherst, Massachusetts, USA.
39. Railway Technical Research Institute (RTRI) (1999) Design standard for Railway Structures - Seismic Design [in Japanese]. Railway Technical Research Institute, Tokyo, Japan.
40. Abu Sayeed M (2016) Design of Ballasted Railway Track Foundations using Numerical Modelling with Special Reference to High Speed Trains. Ph. D Thesis, Curtin University, Australia.
41. Indraratna B, Lackenby J, Christie D (2005) Effect of confining pressure on the degradation of ballast under cyclic loading. Geótechnique 55(4): 325-328.
42. Estaire J, Cuéllar V, Cámara JL, Fernández R, González F (2017) Settlement laws of bed layers of a ballast track as determined in CEDEX Track Box. Conference paper 19^th International Conference of Soil Mechanics and Geotechnical Engineering, Seoul, pp. 1357-60.
43. Chai JC, Miura N (2002) Traffic-Load-Induced Permanent Deformation of Road on Soft Subsoil. J Geotech Geoenviron Eng, 11(907): 128.
44. Gidel G, Hornych P, Chauvin JJ, Breysse D and Denis D (2001) A New Approach for Investigating the Permanent Deformation Behaviour of Unbound Granular Material Using the Repeated Load Triaxial Apparatus. Bullliaison Petch 233: 5-21.
45. Niemunis A, Wichtmann TY, Triantafyllidis T (2005) A high-cycle accumulation model for sand. J Comput Geotech 32(4): 245-263.
46. Wichtmann T, Niemunis A, Triantafyllidis T (2009) Validation and calibration of a high-cycle accumulation model based on cyclic triaxial tests on eight sands. Soils and Foundations 49(5): 711-728.
47. Wichtmann T (2010) Explicit accumulation model for non-cohesive soils under cyclic loading Phd Thesis, Ruhr-Universität Bochum, Bochum, Germany.
48. Chen J, Alonso EE, Gu C, Cao Z, Cai Y (2018) Long term cyclic behavior of unsaturated granular soils. J Transp Geotech 17: 48-55.
49. Karg C, Haegeman W (2009) Elasto-plastic long-term behavior of granular soils: Experimental investigation. J Soil Dynam Earthquake Eng 29(1): 155-172.
50. Li Q, Ling X, Sheng D (2016d) Elasto-plastic behaviour of frozen soil subjected to long-term low-level repeated loading, Part II: Constitutive modelling. J Cold Reg Sci Techno 122: 58-70.
51. Suiker A, de Borst R (2003) A numerical model for the cyclic deterioration of railway tracks. Int J Numer Meth Engng 57(4): 441-470.
52. Kolymbas D (1985) A generalized hypoplastic constitutive law. Proceedings of the eleventh International Conference on Soil Mechanics and Foundation Engineering 5: 2626.
53. Wu W, Kolymbas D (1990) Numerical testing of stability criterion for hypoplastic constitutive equations. Mechanics of Materiales 9(3): 245-252.
54. Von Wolffersdoff PA (1996) A hypoplastic relation for granular materials with a predefined limit state surface. Mechanics of Cohesive-Frictional Materials 1(3): 251-271.
55. Niemunis AY, Herle I (1997) Hypoplastic model for cohesionless soils with elastic strain range. Mechanics of Cohesive-Frictional Materials 2: 279-299.
56. Wichtmann T, Niemunis A, Triantafyllidis T (2010) On the determination of a set of material constants for a high-cycle accumulation model for non-cohesive soils. Int J Anal Meth Geomech 34(4): 409-440.
57. Bi ZQ, Gong QM, Kang Z, Wang LS (2017) An Implicit-Explicit Transition Method for Settlement Prediction of High-Speed Railway Subgrade Under High Cycle Load. In Bian X, Chen Y, Ye X, Environmental Vibrations and Transportation Geodynamics, pp. 785-800.
58. Amrane M, Messat S (2017) Modeling the behavior of geotechnical constructions under cyclic loading with a numerical approach based on J Lemaitre model. J Indian Geotech 47(3): 1-9.
59. Machaček J, Wichtmann T, Zachert H, Triantafyllidis Th (2018) Long-term settlements of a ship lock: Measurement vs. FE-prediction using a high cycle accumulation model. J Comput Geotech 97: 222-232.
60. Chiou JS, Lin HS, Yeh FY, Sung YC (2016) Plastic settlement evaluation of embedded railroads under repeated train loading. J Geo Engineering 11(2): 97-107.
61. Gia Khanh N (2013) Efectos dinámicos debidos al tráfico de ferrocarril sobre la infraestructura de vía y las estructuras, Tesis Doctoral, Universidad Politécnica de Madrid, Madrid, Spain.
62. Ishikawa T, Miura S, Sekine E (2014) Simple plastic deformation analysis of ballasted track under repeated moving-wheel loads by cumulative damage model. J Transp Geotech 1(4): 157-170.
63. Cerni G, Cardone F, Virgili A, Camilli S (2012) Characterisation of permanent deformation behaviour of unbound granular materials under repeated triaxial loading. J Constr Build Mater 28(1): 79-87.
64. Cambou B, Hicher PY (2010) Elastoplastic Modeling of Soils: Cyclic Loading. In Hicher PY, Shao JF, Constitutive Modeling of Soils and Rocks John Wiley & Sons Inc, Hoboken, NJ, USA, pp. 143-185.
65. Hirano K, Jiang GL, Tateyama M, Chikuma S, Tatsuoka F (1997) Deformation and cumulative strain characteristics of sandy filling material [in Japanese]. Proceedings of the 52^nd annual conference of the Japan Society of Civil Engineers, pp. 146-147.
66. Office for Research and Experiments of the International Union of Railways (ORE) (1970) Repeated loading of clay and track foundation design Report no. D 71 / RP 12, Utrech, Netherlands.