 Review Article
Review Article
Solving the Non-Damped Oscillatory Problem with Random Loading Conditions using WHE Technique
Amnah S Al Juhani1* and Aisha M Al Hwiti2
1Tabuk University, Faculty of Science, Saudi Arabia
2Tabuk University, Faculty of Science, Saudi Arabia
Amnah S Al Juhani, Tabuk University Faculty of Science, Saudi Arabia.
Received Date: June 10 , 2019; Published Date: June 17 , 2019
Abstract
The spectral techniques for solving the stochastic differential equations (SDEs) are efficient compared with other techniques. They can be used to obtain analytical solutions specially in case of linear SDEs. Among which, the Wiener-Hermite expansion (WHE) and the Winer Chaos expansion (WCE) are the most common. WHE is more efficient as it depends directly on a basis that is directly dependent on the noise process. It can be used efficiently when the SDE is forced by additive and/or multiplicative noise.
In the current work, WHE is used to analyze the stochastic non-damped oscillatory equation. The corresponding deterministic system is obtained, and solution techniques are suggested and compared. The solution statistics are computed in analytical formulae and compared for different parameters. The efficiency of WHE is outlined as a reliable technique that can be used for any order of approximation in linear and nonlinear SDEs.
Keywords:Linear stochastic differential equations; Wiener-hermite expansion; Linear oscillatory; WHEP technique; Mathematical
Introduction
Since Meecham and his co-workers [1] developed a theory of turbulence involving a truncated Wiener-Hermite expansion (WHE) of the velocity field, many authors studied problems concerning turbulence. Various applications in fluid mechanics was also studied in [2-4]. Scattering problems attracted the WHE applications through many authors. The nonlinear oscillators were considered as an opened area for the applications of WHE as can be found in [5-10]. There are a lot of applications in boundary value problems and generally in different mathematical studies.
The Wiener Hermite Expansion (WHE) was originally developed by Norbert Wiener in 1938-1958 Wiener constructed an orthonormal random bases for expanding homogeneous chaos depending on white noise and used it to study problems in statistical mechanics]. In (WHE) approach, there is no randomness directly involved in the computations, one does not have to rely on pseudo random number generators, and there is no need to solve the stochastic DEs repeatedly for many realizations [11-20].
Instead, the deterministic system is solved only once by converting the problem to a system of deterministic equations that can be solved efficiently using the standard deterministic numerical methods. After that it is easy to determine mean, covariance, and higher order statistical moments, by using simple formulae involving only the deterministic Wiener-Hermite coefficients. The application of WHE aims at finding a truncated series solution of differential equations [21]. The truncated series composes of two major parts, the first is the Gaussian part which consists of the first two terms, while the rest of the series constitute the non-Gaussian part. When solving nonlinear stochastic integrodifferential equations using the WHE, the resultant set of deterministic integrodifferential equations obtained are quite complicated and it is not always possible to find an analytic solution.
Problem Formulation
The main objective of this paper is to solve the following linear oscillatory problem without damping with random loading condition [22].
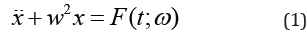
with deterministic initial conditions
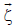
Where w: frequency of oscillation, and the stochastic excitation F (t, ω ) is defined as

where
ε is the deterministic nonlinearity scale,
ω ∈(Ω,σ , P) is the triple probability space with Ω as the sample space,
σ is a σ -algebra on the event space Ω ,
P is a probability measure, and
n (t;ω) is white noise with the following properties:
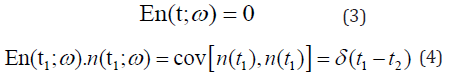
In the following section we will find the probability density function (p.d.f) average and the variance for x(t).
Finding the P.d.f, Average and Variance of x (t):
The general solution of equation (1) is,
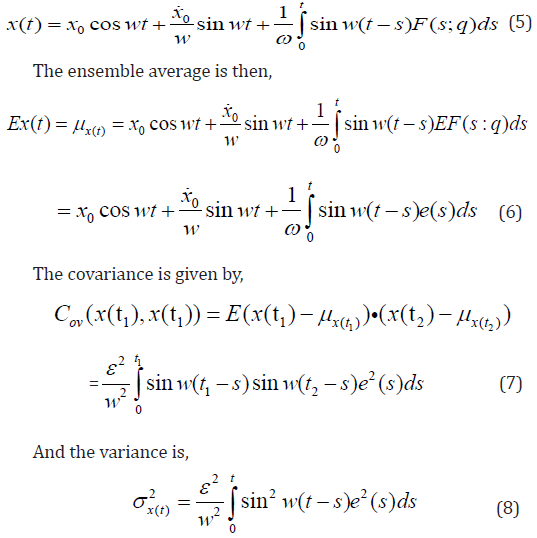
Due to linearity and the deterministic initial conditions we obtain the following Gaussian solution process:
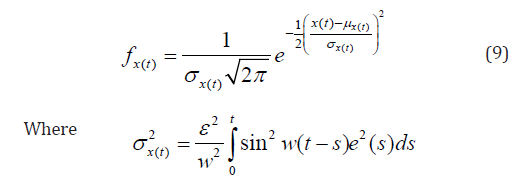
Equation (9) represent a closed form solution of problem (1) with random loading condition.
WHEP Technique
The application of the WHE aims at finding a truncated series solution to the solution process of differential equations. The truncated series composes of two major parts; the first is the Gaussian part which consists of the first two terms, while the rest of the series constitute the non-Gaussian part. In nonlinear cases, there exists always difficulties of solving the resultant set of deterministic integrodifferential equations got from the applications of a set of comprehensive averages on the stochastic integra-differential equation obtained after the direct application of WHE. Many authors introduced different methods to face these obstacles. Among them, the WHEP technique was introduced in [23] using the perturbation technique to solve perturbed nonlinear problems.
The WHE method utilizes the Wiener-Hermite polynomials which are the elements of a complete set of statistically orthogonal random functions [30]. The Wiener-Hermite polynomial H(i) (t1,t2,t3,…ti) satisfies the following recurrence relation:

in which n(t) is the white noise with the following statistical properties
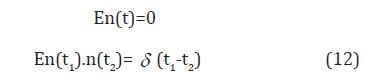
where δ (-) is the Dirac delta function and E denotes the ensemble average operator
The Wiener-Hermite set is a statistically orthogonal set, i.e.

The average of almost all H functions vanishes, particularly,

Due to the completeness of the Wiener-Hermite set, any random function G(t;ω ) can be expanded as
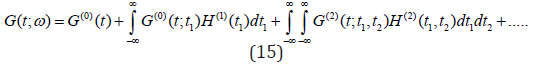
where the first two terms are the Gaussian part of G(t;ω ). The rest of the terms in the expansion represent the non-Gaussian part of G(t;ω ). The average of G(t; ω ) is
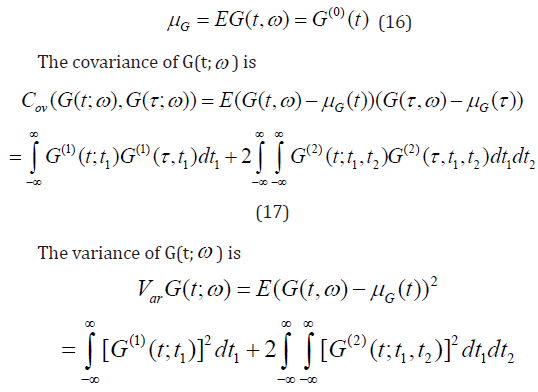
The WHEP technique can be applied to linear or nonlinear perturbed systems described by ordinary or partial differential equations. The solution can be modified in the sense that additional parts of the Wiener-Hermite expansion can always be taken into considerations and the required order of approximations can always be made depending on the computing tool. It can be even run through a package if it is coded in some sort of symbolic languages. The technique was successfully applied to several nonlinear stochastic equations, see [20-22].
Case Study [23-26]
In the previous case of study solve by using WHEP technique.
The following results are obtained:
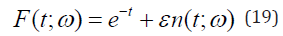
To compensate by the original formula of (10) we get:
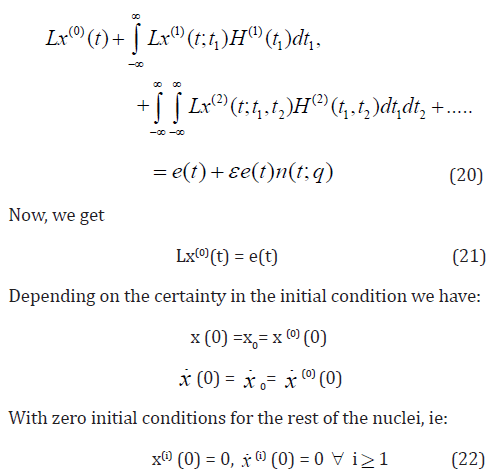
Accordingly, we obtain the following:

It can be show that:

This method is more reliable than others, since we do not have the perturbation problem because the Wiener-Hermite expansion belong to a complete space.
Example:
Consider the following

In the case-study presented in section 4, the following results are obtained (Figures 1-8):
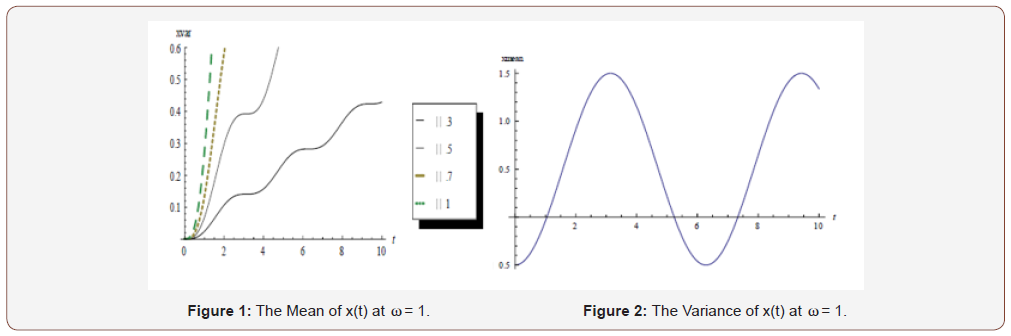
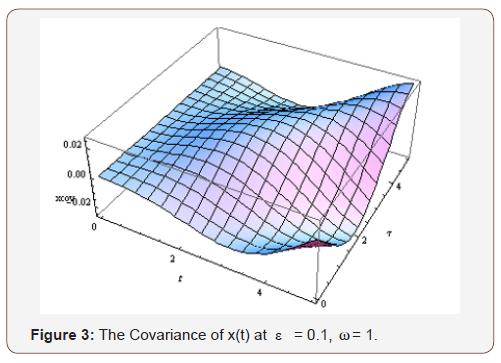
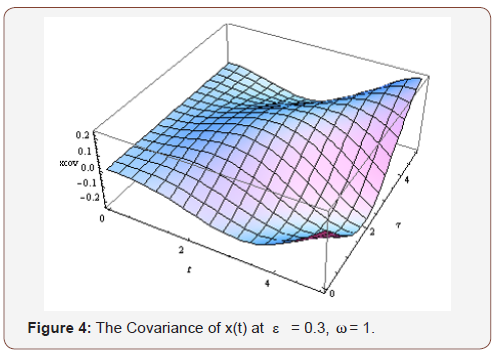
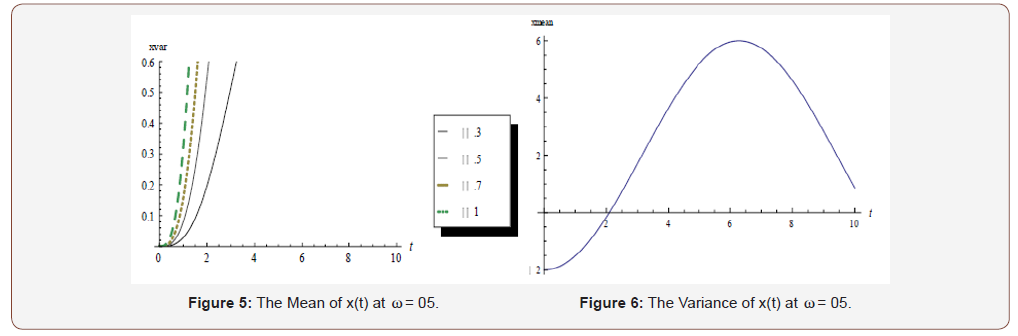
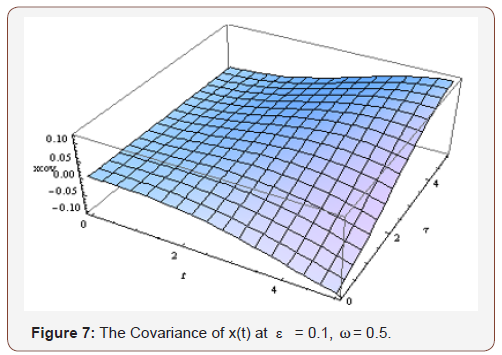
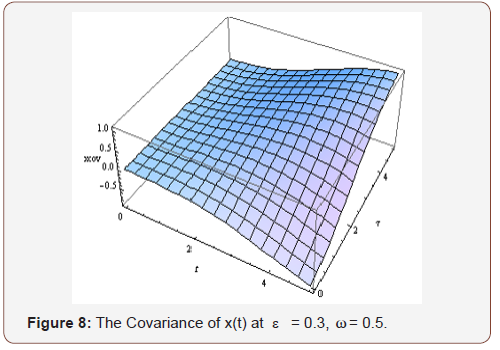
Conclusion
By comparing the solution that we get using this method with the one obtained using the WHEP technique, we found that the two solutions are identical. Where we have considered the Gaussian part only in this comparison. The WHEP technique is a combination of the homotropy perturbation method and the wiener-Hermite technique.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Nayfeh A (1993) Problems in perturbation. Wiley, NY.
- Crow S, Canavan G (1970) Relationship between a Wiener-Hermite expansion and an energy cascade. J of fluid mechanics 41(2): 387-403.
- Saffman P (1969) Application of Wiener-Hermite expansion to the diffusion of a passive scalar in a homogeneous turbulent flow. Physics of fluids 12(9): 1786-1798.
- Kahan W, Siegel A (1970) Cameron-Martin-Wiener method in turbulence and in Burger’s model: General formulae and application to late decay. J of fluid mechanics 41(3): 593-618.
- Wang J, Shu S (1974) Wiener-Hermite expansion and the inertial subrange of a homogeneous isotropic turbulence. physics of fluids 17(6): 1130.
- Hogge H, Meecham W (1978) Wiener-Hermite expansion applied to decaying isotropic turbulence using a renormalized time-dependent base. J of fluid of mechanics 85(2): 325-347.
- Doi, Masaaki, Imamura, Tsutomu (1979) Exact Gaussian solution for two-dimensional incompressible inviscid turbulent flow. J of the physical society of Japan 46(4): 1358-1359.
- Kambe, Ryouichi, Doi, Masaaki, Imamura, Tsutomu (1980) Turbulent flows near flat plates. J of the physical society of Japan 49(2): 763-778.
- Chorin, Alexandre J (1974) Gaussian fields and random flow. J of fluid of mechanics 63(1): 21- 32.
- Kayanuma, Yosuka (1985) Stochastic theory for non-adiabatic crossing with fluctuating off-diagonal coupling. J of the physical society of Japan 54(5): 2037-2046.
- Joelson M, Ramamonjiarisoa A (2003) Random fields of water surface waves using Wiener-Hermite functional series expansions. J of fluid of mechanics 496: 313-334.
- Eftimiu, Cornel (1988) First-order Wiener-Hermite expansion in the electromagnetic scattering by conducting rough surfaces. Radio science 23(5): 769-779.
- Gaol, Nakayama J (1999) Scattering of a TM plane wave from periodic random surfaces. waves random media 9(11): 53-67.
- Tamura Y, Nakayama J (2005) Enhanced scattering from a thin film with one-dimensional disorder. waves in random and complex media 15(2): 269-295.
- Tamura Y, Nakayama J (2005) TE plane wave reflection and transmission from one-dimensional random slab. IEICE transactions on electronics, E88-C (4): 713-720.
- Skaropoulos N, Chrissoulidis D (1999) Rigorous application of the stochastic functional method to plane wave scattering from a random cylindrical surface, J of mathematical physics 40(1): 156- 168.
- Jahedi A, Ahmadi G (1983) Application of Wiener-Hermite expansion to non-stationary random vibration of a Duffing oscillator, J. of applied mechanics, Transactions ASME 50(2): 436- 442.
- Orabi, Ismail I, Ahmadi A, Goodarz (1987) Functional series expansion method for response analysis of nonlinear systems subjected to ransom excitations. Int J of nonlinear mechanics 22(6): 451- 465.
- Orabi, Ismail I (1988) Response of the Duffing oscillator to a non- Gaussian random excitation. J of applied mechanics, Transaction of ASME 55(3): 740-743.
- Abdel Gawad E, El-Tawil M, Nassar MA (1989) Nonlinear oscillatory systems with random excitation. Modeling, Simulation and Control –B 23(1): 55-63.
- Orabi, Ismail I, Ahmadi A, Goodarz (1991) New approach for response analysis of nonlinear systems under random excitation, American society of mechanical engineers, design engineering division (publication) DE 37: 147-151.
- Gawad E, El Tawil M (1993) General stochastic oscillatory systems. Applied Mathematical Modelling 17(6): 329-335.
- El Tawil M, Mahmoud G (1999) The solvability of parametrically forced oscillators using WHEP technique, Mechanics and mechanical engineering 3(2): 181-188.
- Tamura Y, Nakayama J (2003) A formula on the Hermite expansion and its application to a random boundary value problem. IEICE Transactions on electronics E86-C (8): 1743-1748.
- El Tawil M (2003) The application of WHEP technique on stochastic partial differential equations. Int J of differential equations and applications 7(3): 325-337.
- Kayanuma Y, Noba K (2001) Wiener-Hermite expansion formalism for the stochastic model of a driven quantum system. Chemical physics 268(1-3): 177-188.
-
Amnah S Al Juhani, Aisha M Al Hwiti. Solving the Non-Damped Oscillatory Problem with Random Loading Conditions using WHE Technique. Glob J Eng Sci. 2(4): 2019. GJES.MS.ID.000544.
-
Linear stochastic differential equations; Wiener-Hermite expansion; Linear oscillatory; WHEP technique; Mathematica
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






