Numerical Computation of Separation Events

Impact oscillators give rise to nonlinear behavior through the abrupt, impulsive interaction between the distinct, interacting bodies. Modeling this behavior accurately is a challenge because the instant of impact is not known a-priori. Moreover, capturing the instant of impact is crucial because nonlinear systems can display an extreme sensitivity to initial conditions, i.e., an impact event can be viewed as an initial condition for a new trajectory. For cases where the motion is found numerically via a time-stepping algorithm, Henon [1] developed a simple numerical technique for ascertaining this instant of impact. This method has been used effectively in a number of impact problems and produces results that agree with other techniques and, more importantly, with independent experimental observations. It has also been incorporated into commercial software packages.

One common model for an impact oscillator uses the coefficient of restitution (CoR) [2]. Here, the normal component of the rebound velocity is given as a percent of the inbound (pre-collision) velocity. It is assumed that, provided e≠0, the interacting bodies come into contact and then immediately separate. When numerically timestepping a solution, Henon’s method is invaluable because it clearly indicates the instant when the impact event occurs, i.e., when the CoR model should be applied.

Another class problem that comes up from time to time is that of separation. One can imagine two (or more) contacting bodies moving together; in this case, the system can be modeled as a single degree of freedom problem with one combined mass. As the motion evolves, these bodies may separate. This requires a sudden change in the model from one degree of freedom to multiple degrees of freedom. Therefore, like the impact problem, determining the moment of separation is critical in order to generate the response accurately. However, unlike the impact problem, the separation event is more subtle. It is not dictated by a condition placed on one of the state variables. Instead, the system must be unpacked a bit before a Henon-like approach may be taken (Figure 1).

In this paper a numerical technique is developed to determine this instant of separation for these systems. This method takes its inspiration from Henon’s method. Consequently, Henon’s method is briefly reviewed. Next, the separation problem is described and a numerical technique for the instant of separation is developed. A number of examples are provided, which demonstrate the utility of the method.

The numerical solution of nonlinear ordinary differential equations involves time-stepping. This process begins by writing the set of equations in first order form: ẋ = f(x(t), t). x is the unknown state vector and t is the independent variable. Solutions are obtained by starting at some initial condition and integrating the state variables through some discrete time step △t from to t0 to t1. This integration is accomplished by some numerical scheme, such as Runge-Kutta, Geer’s method, etc. [3]. Using x(t1) as a new initial condition, another time integration step △t may be taken to t2. This gives x(t2). This process continues and gives the timediscretized trajectory of the system.

As will be described, both of the impact and separation problems are nonlinear in the sense that there is a model change at the impact/separation event. So, it is critical to ascertain the instant of these events or else the computed trajectories will not faithfully reflect the system response. As motivation, the impact problem is outlined and a brief description of the Henon technique [1] is given in the next section. This is followed, in the subsequent section, by a description of the separation problem and the new numerical technique for handling that problem.

Impact events

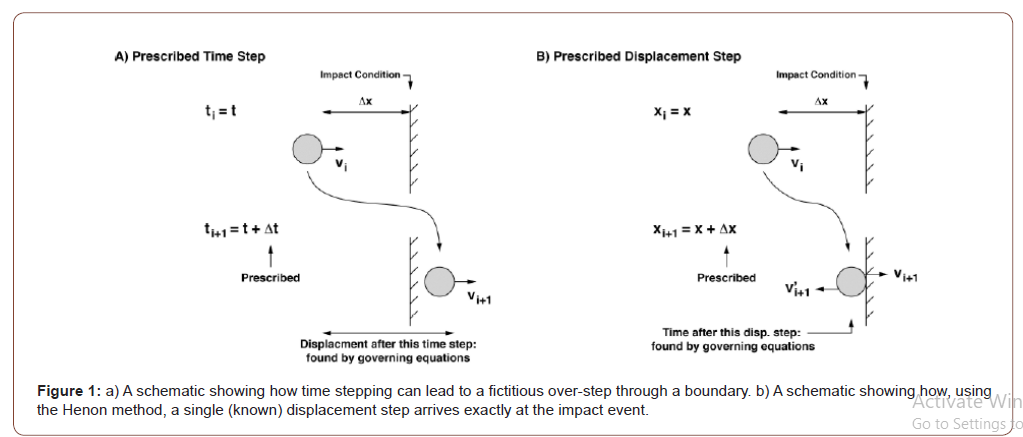
For the moment, consider a single mass approaching a rigid wall along its normal direction; this is shown schematically in Figure (1a). The equations of motion for the ball may be integrated until the mass impacts the wall. At the moment of impact, the velocity is instantaneously changed. The post-impact velocity υ’ (which serves as the new initial condition for the next step in the integration) is found by reversing the direction of the pre-impact velocity v and multiplying it by the coefficient of restitution: υ’= -eυ. However, to apply this condition, it is assumed that the integration routine will land exactly at the impact event (the wall). In general, this does not happen.

To demonstrate this, again consider Figure (1a). The equations of motion for the mass have been integrated through i time steps to ti. This leaves the mass very near the wall, △x away from an impact. The integration routine steps to ti+1; the updated position of the mass is determined by the governing differential equations. This turns out to be on the other side of the impact condition, which is physically meaningless since the mass can’t penetrate the wall. Traditional routines would return to t_i and proceed to take smaller time steps, in the hope of landing “close enough” to the impact condition. But this process of refining the time step is computationally laborious. Moreover, it won’t effectively find the moment of impact because the same issue will continue to crop up, just at smaller spatial and temporal scales (Figure 2).

Henon [1] came up with a practical and easy-to-implement technique to circumvent this problem. Here is an overview. Consider Figure (1b). The problem begins at the same instant t_i and position xi as before. Because the distance to the wall is well known (but the time needed to get there is not), the problem is recast. Specifically, the equations are rewritten with x as the independent variable and ẋ and t as the dependent variables. Then, rather than taking a time step, the system undertakes a single displacement step of △x. This, by definition, lands the mass at the impact condition. The associated velocity and time are determined by the recast differential equations. At this instant, the velocity is changed to the post-impact value: υ’ = -eυ. Then the equations are returned to their original form (with t as the independent variable) and the time stepping algorithm is continued until the next impact event.

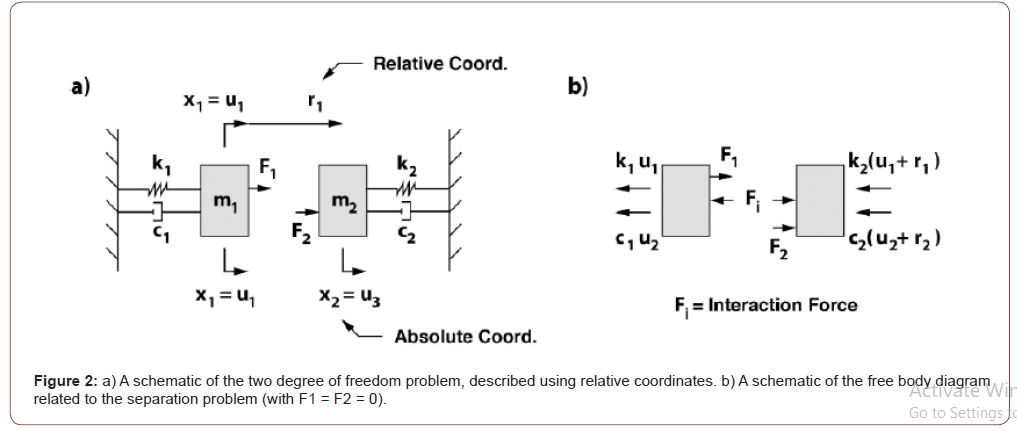
As a specific example, consider the two linear, forced massspring- dampers, shown in Figure (2a). The equations of motion may be expressed in first order form with {u₁, u₂}t being the absolute displacement and velocity of the first mass. Similarly, {u₃, u₄}t are the absolute displacement and velocity of the second mass. With no coupling between the two masses the equations of motion are:

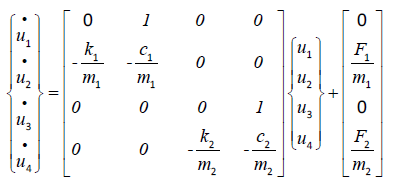
These equations are only valid in the free-play region, when the masses are not in contact. To find the instant of impact, the equations are first rewritten in terms of the absolute displacement and velocity for mass one (u₁; u₂) and the relative displacement and velocity of mass two (r₁; r₂). See Figure (2a). In terms of these coordinates, Eq. (1) takes the form:

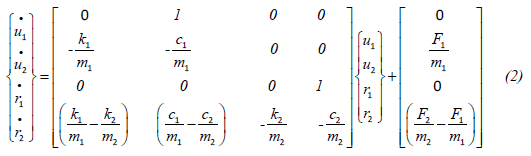
The relative coordinate r₁ provides direct access to the gap between the masses; contact is indicated by the condition r₁ = 0. Next, r₁ replaces t is as the independent variable. This is accomplished

To integrate the system through an impact event, Eqs. (2) are time integrated until the position violates the impact condition (i.e., the two bodies pass through one another, similar to Figure (1a)). Taking a time step back, one then switches to Eq. (3) and takes a prescribed relative displacement step (r1) to the impact condition. The other dependent variables (including time, t) are obtained through the integration process. Once at the impact condition, the velocities are changed using the CoR model and time stepping may resume using Eq. (2).

Separation events

Various conditions may cause two (or more) bodies to move together. Initial conditions could be such that they all begin together. Or two objects may approach one another, and their velocities coalesce at impact, causing them to move together afterwards. Regardless of the cause, consider two contacting bodies that are moving together. This scenario opens the door to the possibility that they may separate. Normal time integration of the governing equations will typically step through the separation event - just as time integration usually steps through an impact event (see Figure (1a)). Now the parallel question is asked: can the equations be recast in such a way as to end up at the moment of separation? As a specific example, recall the two degree of freedom model of Figure (2a) with u1 = u2 (or r1 = 0). There is an interaction force Fi between the bodies, as shown in Figure (2b). Applying Newton’s law to each mass and ignoring the external forces (for the moment) gives:

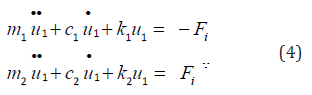
Summing these equations eliminates the unknown, time dependent force Fi and leaves a single, second order ODE for the system motion:

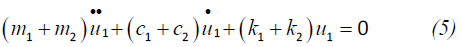
In other words, the system may be viewed as a single degree of freedom, equivalent system. Once u₁ is determined by integration, the interaction force may easily be found at each time step by the above equation(s).

Separation occurs when the interaction force F_i is reduced to zero. At that instant, the system reverts to a two degree of freedom model, Eq. (1) (or, alternatively, Eq. (2)). The challenge here is to find the moment when F → 0 and the masses separate. In this problem, one must take a force step to zero (F_i = 0), rather than a displacement step, as was done in the impact problem. Hence, the governing equations must be re-cast so that the independent variable is changed from t to F_i.

In the impact problem, it was easy to switch the independent variable to the relative position (r₁) because the set of ODE’s

So, in summary, as the masses move together, Eq. (11) is integrated forward in time. Once a separation event is detected

( i F ≤ 0 ), the system is taken back one-time step to its prior state. Then Eq. (12) is integrated with a single interaction force step, which takes Fi from its current value to zero. After separation the system reverts to the free-play equations, either Eq. (1) or Eq. (2).

The utility of these methods are demonstrated using the same simple two degree of freedom system shown in Figure (2). All of the mechanical elements are linear. The system is governed by Eq. (2) when the masses are apart and by Eq. (11) when the masses move together. Impact and separation events are identified by Eqs. (3) and (12), respectively. Both numerical and analytical solutions are sought.

Numerical solutions

All numerical solutions are obtained by a standard fourth order Runge-Kutta algorithm [3]. The numerical techniques for impact and separation, described in the previous section, are employed. No numerical stability issues were encountered in these simulations.

Analytical solutions

The governing equations are all linear and can be solved analytically. However, the time when a transition (impact/ separation) occurs is unknown a-priori but may be determined numerically, as described previously. Also see reference [4].

The solution for motion in the free play region is trivial since the state matrix is at full rank. For brevity sake, that solution is not presented here. When the masses move together, the situation changes: Eq. (11) contains two zero columns and, hence, is rank deficient. These equations may be written in matrix form: V=AV. In this case,

The first and second eigenvectors are acceptable because the first and fourth columns of A are zeros, meaning that the first and fourth elements of q₁ and q₂ are arbitrary and are selected to be one. The second and third elements of these two vectors must be zero because the second and third columns are nonzero. The other two eigenvectors, q3 and q4, are found in the usual way. Provided these vectors are linearly independent (see appendix), the solution takes the form:

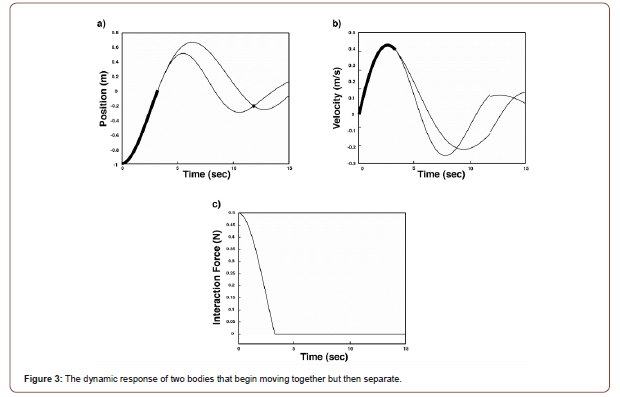
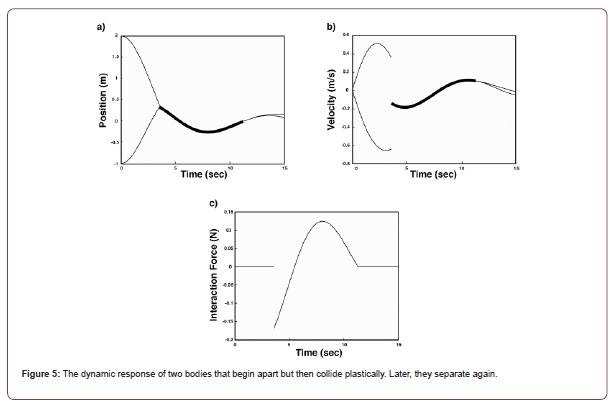
The absolute positions of the two masses are shown in Figure (3a). The analytical and numerical solutions are shown and are coincident. Initially, the two masses move together until approximately 3.26s where they experience a separation event. The contacting portion of the motion is indicated in the figure with a thicker line. Using the force step algorithm, this event is captured at the moment when Fi → 0. After this, the masses are in the free play region. And then at approximately 11.83s, the masses impact one another. Here, the moment of this impact is captured using the displacement step algorithm. But because the velocities are not equal just prior to the impact (i.e., the trajectories don’t approach one another tangentially) and the coefficient of restitution is sufficiently large, the masses rebound off of one another. This is clear from Figure (3b), which shows the associated velocities. Had the trajectories approached one another tangentially or had e been sufficiently small, they may have started moving together. This will be demonstrated in the next example. Figure (3c) shows the interaction force as a function of time. Note that the impact force (at t ≈ 11.83s) is not included here. This figure highlights the fact that the moments of separation and impact are faithfully described (Figure 4).

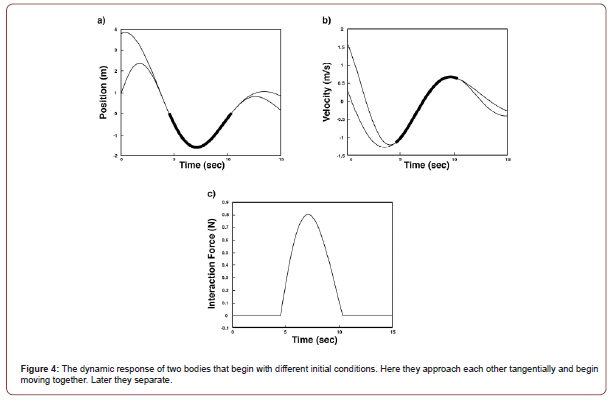
Grazing impact and separation: In this case, the two masses start out with different initial conditions. However, the initial conditions are chosen such that the trajectories approach one another tangentially. In other words, the two masses graze one another, allowing for a collision with equal outgoing velocities. So, the masses begin to move together. The initial conditions for the two

As before, Figures (4a,4b,4c) show the system displacement, velocity and interaction force, respectively, for these initial conditions. The numeric and analytic solutions are plotted and are coincident. Figure (4a) shows the trajectories approaching one another tangentially. The displacement step algorithm determines the moment of contact at approximately t = 4.53s where the masses being moving together, shown by the thicker line. At that same instant, the interaction force ((4c)c) becomes nonzero. This contacting motion persists until approximately t = 10.s36s, when the two masses experience a separation event. This can be seen in Figures (4a) and (4b) but is perhaps most obvious in Figure (4c), where the interaction force clearly goes to zero.

This work presents a new technique for calculating numerically the moment of separation of two moving, contacting bodies. This approach builds off of the technique developed by Henon [1] for determining numerically the moment of impact for two moving bodies. Specifically, the governing equations are integrated numerically until the impact condition is violated (i.e., the last time step went beyond the impact condition, allowing the bodies to partially pass through one another). The system then goes back one-time step, where the distance to impact is known. The governing equations are recast so with the relative position of the two bodies being the independent variable.

Time t is a dependent variable to be determined by the integration routine. A single displacement step is taken exactly to the condition of first contact. The associated time is then computed from the recast equations, along with the other state variables. In a similar way, the onset of separation of two contacting bodies may be identified. The system may be integrated forward in time until a separation event takes place. Going back one-time step, the governing equations may be recast so that the independent variable is the interaction force between the two bodies. Then a single force step may be taken to the exact moment of separation (F → 0). The process of recasting the equations is demonstrated with a simple two mass problem. To highlight the implementation, a number of impact/separation cases are considered both numerically and analytically. In each scenario, the instant of contact/separation are precisely identified, and the ensuing motion found. In general, the method developed here is straightforward and effective. And it may be easily extended for systems containing more degrees of freedom.

The authors would like to thank Quentin Pollett and Paul Davis for their valued input.

There are no conflicts of interest related to this work.