Journal Flyer

Global Journal of Engineering Sciences - GJES

ISSN: 2641-2039

Managing Editor: Lisa Debora

Contact us at:

Open Access Mini Review

Nonlinear Mechanics of Microstructures

Ali Farajpour1, Mergen H Ghayesh1 and Hamed Farokhi2*

1Department of Mechanical Engineering, University of Adelaide, Australia

2Department of Mechanical and Construction Engineering, Northumbria University, UK

Corresponding Author

Received Date: February 12, 2019;  Published Date: February 21, 2019

Abstract

In this paper, a brief review is presented on the influence of nonlinearity on the mechanics of microscale structures. The constitutive equations of size-dependent elasticity-based theories such as the couple stress are presented. The linear size-dependent elasticity-based models of microscale structures are discussed. Furthermore, the effects of different types of nonlinearity on the static stability, oscillation and static deformation of microscale structures are reviewed.

Keywords: Microstructures; Modified elasticity; Geometrical nonlinearity; Size effects

Introduction

The mechanical behaviour of microscale structures such as microscale beams and plates are highly nonlinear in many practical cases due to large applied forces as well as strong interactions between different parts at microscales. In applications such as resonators, sensors and generators, in which the mechanical behaviour plays a crucial role, understanding the nonlinear response becomes important [1-5]. In recent years, a number of size-dependent elasticity-based models have been used to analyze the static stability, time-dependent deformation and static deformation of the structural components of microscale and nanoscale systems [6-9]. The appropriate elasticity-based model is selected according to the size of the structural component. The couple stress and strain gradient theories as well as their modified versions are mainly utilised for structures at microscales [10-15]. However, the nonlocal elasticity-based models such as the pure nonlocal elasticity [16-23] and nonlocal strain gradient elasticity [24-28] are reasonable for nanoscale structures.

Linear Analysis of Microscale Structures

To analyse the linear mechanics of microscale structures, modified couple stress models have extensively been employed. According to this theory, one can write [4,32].

irispublishers-openaccess-engineering-sciences


irispublishers-openaccess-engineering-sciences


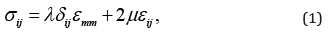
in which λ and μ are employed to represent the Lamé constants; γ is the size parameter; δij , mij and χij denote the Dirac delta function, deviatoric couple stress and symmetric curvature, respectively[33]. Equations (1) and (2) have extensively been utilised for examining the linear [15,34] and nonlinear [35- 37] mechanical behaviour of microscale structural components.

Stretching-Type Nonlinearity

In large deformations, due to the stretch of the middle surface of plates and the center line of tubes, the effects of nonlinear strains become significant. The effects of stretching-type nonlinearity on the mechanics of microstructures have been analyzed [10,36,38- 43]. Size-dependent models incorporating stretching-type nonlinearity have been developed for various microscale structures such as beams [39,44,45], plates [10,41,46] and shells [40,47]. For the formulation of mechanical behaviour, the couple stress model is used for structural components at microscales [11,35,36,48- 50]. More recently, an elasticity-based model with consideration of both strain gradient and nonlocal effects has been proposed for the large-amplitude dynamics of ultrasmall tubes incorporating the stretching-type nonlinearity [25,26,51].

Curvature-Type Nonlinearity

For particular types of microscale structures such as microcantilevers, the curvature-type nonlinearity becomes important. Taking into account this type of geometrical nonlinearity in these systems yields a more reliable continuum model for investigating the static and dynamic responses. Size-dependent continuum models incorporating curvature-type nonlinearity have been developed for the large-amplitude vibration [52], dynamics [53,54], stability [55] and modal interaction [56] of ultra-small cantilevers. In addition, the effects of curvature-type nonlinearity on the nonlinear mechanics of functionally graded microcantilevers have lately been analyzed [56-58].

Conclusion

A brief review was presented in this paper for the nonlinear analysis of microscale structural components including microscale beams and plates. It was concluded that for microscale beams with clamped-free boundary conditions (i.e. cantilevers), both types of geometrical nonlinearity are important while for microscale beams with pinned-pinned and clamped-clamped boundary conditions, the stretching-type nonlinearity is dominant. Although a few nonlinear models have been proposed for the large deformation of microscale structures, more investigation is required to better understand the effect of different types of nonlinearity on the mechanical behavior at microscale levels.

Acknowledgement

None.

Conflict of Interests

No Conflict of Interest.

References
  1. M Şimşek (2016) Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel Hamiltonian approach. International Journal of Engineering Science 105: 12-27.
  2. H Farokhi, MH Ghayesh (2018) Nonlinear mechanics of electrically actuated microplates. International Journal of Engineering Science 123: 197-213.
  3. MH Ghayesh (2018) Nonlinear vibrations of axially functionally graded Timoshenko tapered beams. Journal of Computational and Nonlinear Dynamics 13(4): 041002.
  4. MH Ghayesh (2018) Mechanics of tapered AFG shear-deformable microbeams. Microsystem Technologies 24: 1743-1754.
  5. MH Ghayesh (2018) Functionally graded microbeams: Simultaneous presence of imperfection and viscoelasticity. International Journal of Mechanical Sciences 140: 339-350.
  6. AG Shenas, S Ziaee, P Malekzadeh (2017) Nonlinear vibration analysis of pre-twisted functionally graded microbeams in thermal environment. Thin-Walled Structures 118: 87-104.
  7. T Murmu, M McCarthy, S Adhikari (2012) Vibration response of doublewalled carbon nanotubes subjected to an externally applied longitudinal magnetic field: a nonlocal elasticity approach. Journal of Sound and Vibration 331: 5069-5086.
  8. MH Ghayesh, H Farokhi, A Gholipour, S Hussain (2017) Complex motion characteristics of three-layered Timoshenko microarches. Microsystem Technologies 23: 3731-3744.
  9. MH Ghayesh, H Farokhi (2018) Nonlinear behaviour of electrically actuated microplate-based MEMS resonators. Mechanical Systems and Signal Processing 109: 220-234.
  10. H Farokhi, MH Ghayesh (2018) On the dynamics of imperfect shear deformable microplates. International Journal of Engineering Science 133: 264-283.
  11. MH Ghayesh (2018) Dynamics of functionally graded viscoelastic microbeams. International Journal of Engineering Science 124: 115-131.
  12. MH Ghayesh, H Farokhi (2018) On the viscoelastic dynamics of fluidconveying microtubes. International Journal of Engineering Science 127: 186-200.
  13. MH Ghayesh, H Farokhi, A Gholipour, M Tavallaeinejad (2018) Nonlinear oscillations of functionally graded microplates. International Journal of Engineering Science 122: 56-72.
  14. Ç Demir, Ö Civalek (2017) On the analysis of microbeams. International Journal of Engineering Science 121: 14-33.
  15. MZ Nejad, A Hadi, A Farajpour (2017) Consistent couple-stress theory for free vibration analysis of Euler-Bernoulli nano-beams made of arbitrary bi-directional functionally graded materials. Structural Engineering and Mechanics 63: 161-169.
  16. D Karličić, M Cajić, T Murmu, S Adhikari (2015) Nonlocal longitudinal vibration of viscoelastic coupled double-nanorod systems. European Journal of Mechanics-A/Solids 49: 183-196.
  17. M Farajpour, A Shahidi, A Farajpour (2018) A nonlocal continuum model for the biaxial buckling analysis of composite nanoplates with shape memory alloy nanowires. Materials Research Express 5: 035026.
  18. M Farajpour, A Shahidi, A Hadi, A Farajpour (2018) Influence of initial edge displacement on the nonlinear vibration, electrical and magnetic instabilities of magneto-electro-elastic nanofilms. Mechanics of Advanced Materials and Structures.
  19. MR Farajpour, A Shahidi, A Farajpour (2018) Resonant frequency tuning of nanobeams by piezoelectric nanowires under thermo-electromagnetic field: a theoretical study. Micro & Nano Letters 13: 1627-1632.
  20. SR Asemi, A Farajpour (2014) Vibration characteristics of doublepiezoelectric- nanoplate-systems. IET Micro & Nano Letters 9: 280-285.
  21. Farajpour, A Rastgoo, M Farajpour (2017) Nonlinear buckling analysis of magneto-electro-elastic CNT-MT hybrid nanoshells based on the nonlocal continuum mechanics. Composite Structures 180: 179-191.
  22. Farajpour, MH Ghayesh, H Farokhi (2018) A review on the mechanics of nanostructures. International Journal of Engineering Science 133: 231- 263.
  23. MH Ghayesh, A Farajpour (2019) A review on the mechanics of functionally graded nanoscale and microscale structures. International Journal of Engineering Science 137: 8-36.
  24. M Farajpour, A Shahidi, F Tabataba’i-Nasab, A Farajpour (2018) Vibration of initially stressed carbon nanotubes under magneto-thermal environment for nanoparticle delivery via higher-order nonlocal strain gradient theory. The European Physical Journal Plus 133: 219.
  25. Farajpour, H Farokhi, MH Ghayesh, S Hussain (2018) Nonlinear mechanics of nanotubes conveying fluid. International Journal of Engineering Science 133: 132-143.
  26. Farajpour, H Farokhi, MH Ghayesh (2019) Chaotic motion analysis of fluid-conveying viscoelastic nanotubes. European Journal of Mechanics-A/Solids 74: 281-296.
  27. MH Ghayesh, H Farokhi, A Farajpour (2019) Global dynamics of fluid conveying nanotubes. International Journal of Engineering Science 135: 37-57.
  28. MH Ghayesh, A Farajpour (2018) Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. International Journal of Engineering Science 129: 84-95.
  29. M Aydogdu, I Elisha off (2014) On the vibration of nanorods restrained by a linear spring in-span. Mechanics Research Communications 57: 90- 96.
  30. Farajpour, A Rastgoo, M Mohammadi (2017) Vibration, buckling and smart control of microtubules using piezoelectric nanoshells under electric voltage in thermal environment. Physica B Condensed Matter 509: 100-114.
  31. P Malekzadeh, M Shojaee (2015) A two-variable first-order shear deformation theory coupled with surface and nonlocal effects for free vibration of nanoplates. Journal of Vibration and Control 21: 2755-2772.
  32. H Farokhi, MH Ghayesh, A Gholipour, S Hussain (2018) Resonant responses of three-layered shear-deformable microbeams. Microsystem Technologies 24: 2123-2136.
  33. MH Ghayesh, H Farokhi (2015) Coupled longitudinal-transverserotational behaviour of shear deformable microbeams. Composites Part B: Engineering 77: 319-328.
  34. Y Li, Es Pan (2015) Static bending and free vibration of a functionally graded piezoelectric microplate based on the modified couple-stress theory. International Journal of Engineering Science 97: 40-59.
  35. MH Ghayesh, H Farokhi (2015) Chaotic motion of a parametrically excited microbeam. International Journal of Engineering Science 96: 34- 45.
  36. MH Ghayesh, H Farokhi, G Alici (2016) Size-dependent performance of micro gyroscopes. International Journal of Engineering Science 100: 99- 111.
  37. Gholipour, H Farokhi, MH Ghayesh (2015) In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dynamics 79: 1771-1785.
  38. H Farokhi, MH Ghayesh (2017) Nonlinear resonant response of imperfect extensible Timoshenko microbeams. International Journal of Mechanics and Materials in Design 13: 43-55.
  39. H Farokhi, MH Ghayesh (2017) Viscoelastic resonant responses of shear deformable imperfect microbeams. Journal of Vibration and Control 1077546317699345.
  40. H Farokhi, MH Ghayesh (2018) Nonlinear mechanical behaviour of micro shells. International Journal of Engineering Science 127: 127-144.
  41. H Farokhi, MH Ghayesh (2019) Viscoelastic shear deformable microplates: Nonlinear forced resonant characteristics. Mechanical Systems and Signal Processing 118: 742-756.
  42. H Farokhi, MH Ghayesh, S Hussain (2016) Dynamic stability in parametric resonance of axially excited Timoshenko microbeams. Meccanica 51: 2459-2472.
  43. MH Ghayesh, H Farokhi (2016) Parametric instability of microbeams in supercritical regime. Nonlinear Dynamics 83: 1171-1183.
  44. MH Ghayesh, H Farokhi, G Alici (2015) Subcritical parametric dynamics of microbeams. International Journal of Engineering Science 95: 36-48.
  45. H Farokhi, MH Ghayesh, A Gholipour, S Hussain (2017) Motion characteristics of bilayered extensible Timoshenko microbeams. International Journal of Engineering Science 112: 1-17.
  46. H Farokhi, MH Ghayesh, A Gholipour, M Tavallaeinejad (2017) Nonlinear oscillations of viscoelastic microplates. International Journal of Engineering Science 118: 56-69.
  47. MH Ghayesh, H Farokhi (2017) Nonlinear mechanics of doubly curved shallow microcells. International Journal of Engineering Science 119: 288-304.
  48. MH Ghayesh (2019) Viscoelastic dynamics of axially FG microbeams. International Journal of Engineering Science 135: 75-85.
  49. MH Ghayesh, M Amabili, H Farokhi (2013) Three-dimensional nonlinear size-dependent behaviour of Timoshenko microbeams. International Journal of Engineering Science 71: 1-14.
  50. 50. MH Ghayesh, A Farajpour (2018) Vibrations of shear deformable FG viscoelastic microbeams. Microsystem Technologies.
  51. Farajpour, MH Ghayesh, H Farokhi (2018) Large-amplitude coupled scale-dependent behaviour of geometrically imperfect NSGT nanotubes. International Journal of Mechanical Sciences.
  52. MH Ghayesh, H Farokhi, A Gholipour, S Hussain (2017) On the nonlinear mechanics of layered microcantilevers. International Journal of Engineering Science 120: 1-14.
  53. H Farokhi, MH Ghayesh, S Hussain (2016) Large-amplitude dynamical behaviour of microcantilevers. International Journal of Engineering Science 106: 29-41.
  54. H Farokhi, MH Ghayesh (2015) Dynamical behaviour of electrically actuated microcantilevers. Coupled systems mechanics 4: 251-262.
  55. MH Ghayesh (2018) Stability and bifurcation characteristics of viscoelastic microcantilevers. Microsystem Technologies 1-8.
  56. H Farokhi, MH Ghayesh, A Gholipour, S Hussain (2018) Modal interactions and energy transfers in large-amplitude vibrations of functionally graded microcantilevers. Journal of Vibration and Control 24: 3882-3893.
  57. H Farokhi, MH Ghayesh, A Gholipour (2017) Dynamics of functionally graded micro-cantilevers. International Journal of Engineering Science 115: 117-130.
  58. MH Ghayesh (2019) Mechanics of viscoelastic functionally graded microcantilevers. European Journal of Mechanics-A/Solids 73: 492-499.
Article Details
Citation

  • Ali Farajpour, Mergen H Ghayesh, Hamed Farokhi. Nonlinear Mechanics of Microstructures. Glob J Eng Sci. 1(4): 2019. GJES. MS.ID.000518.

Keywords

  • Microstructures, Modified elasticity, Geometrical nonlinearity, Size effects, Microscale Structures, Microcantilevers, Cantilevers, Static stability

Signup for Newsletter
  • irispublishers-openaccess-engineering-sciences
Scroll to
© 2018 Iris Publishers LLC, All rights reserved. No part of this content may be reproduced or transmitted in any form or by any means as per the standard guidelines of fair use. Creative Commons License Open Access by
Iris Publishers LLC is licensed under Creative Commons License a Creative Commons Attribution 4.0 International License. Based on a work at www.irispublishers.com. Best viewed in browser_icons browser_icons | Above IE 9.0 version | Privacy Policy
Scroll to Top