Investigation of Shock-Boundary Layer Interaction in a Ramp Flow with MVG Under Different Turbulent Inflows

Shock-boundary layer interactions (SBLI) in high-speed flows can significantly reduce the quality of the flow field by inducing large flow separation, causing flow unsteadiness and total pressure loss. The performance and the overall propulsive efficiency of the engine of a high-speed vehicle will be degraded [1-3].

MVG is a potentially new device which can alleviate or overcome the adverse effects of SBLI and, therefore, to improve the “health” of the boundary layer [4-9]. The height of MVGs are usually less than the boundary layer thickness (20-90% of the boundary layer thickness). The small size of the MVGs allows them to be embedded inside the boundary layer, hence reducing the parasitic drag relative to the conventional full size vortex generator. The improved physical understanding of how MVGs reduce shock-induced boundary layer separation will add significantly to the understanding of SBLI that dominate high-speed aerodynamics. In addition, optimized MVG configurations that destabilize the wake and improve the “health” of the boundary layer more efficiently should be studied [10-12].

In previous work [13-15], we performed numerical simulations of supersonic ramp flow with MVG control at M=2.5 and Re=5760 to understand the flow structures, especially the 3D vortex structures, behind the MVG. The flow field around the MVG and surrounding areas have been studied in detail. According to the analysis, a dynamic vortex model was provided. The results of our LES also showed that there exist a series of ring-like (or Ω shaped) vortices [13,14,16] which are formed behind MVG and then travel downstream. Furthermore, it is pointed out that the shock waves at the ramp corner are weaken substantially under the interaction of boundary layer contains ring-like vortices at the upper bound [17].

To confirm that the series of ring-like vortices generated by MVG is the major mechanism of flow separation reduction at the ramp corner, the influence on SBLI under turbulent inflows with different boundary layer thickness (or different relative heights between the MVG and the inlet turbulent boundary layer) are studied. The rest of the paper is organized as follows: In Sec.2, the numerical methods we used are briefly introduced. In Sec. 3, the flow structures especially the ring-like vortices are introduced. The influence on the ring-like vortical structure with different inlet flows are discussed; in Sec. 4. The special SBLI between the ringlike vortices and ramp shock wave under different inlet flows are studied; in Sec. 5. A summary of the present study is provided.

Numerical Methods, Grids and Turbulent Inflows

To reveal the mechanism and get deep understanding of the mechanism of MVG, high order DNS/LES is necessary. Our LES solved the unfiltered form of the Navier-Stokes equations with the 5th order bandwidth-optimized WENO scheme at M=2.5 and Re=5760.

The governing equations are the non-dimensional Navier- Stokes equations in conservative form as follows:

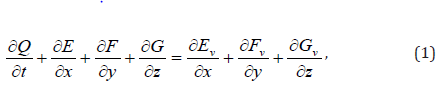
where

in which p denotes the pressure, e is the inner energy and T represents the temperature. The dynamic viscosity is given by Sutherland’s equation [19].

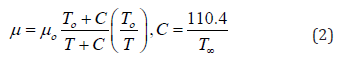
Non-dimensional variables are defined as follows:

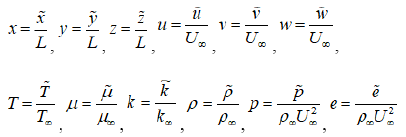
where the variables with ‘∼’ are the dimensional counterparts.

Since the domain is not regular, the Navier-Stokes equations in curvilinear coordinate system are actually solved. Considering the following grid transformation,

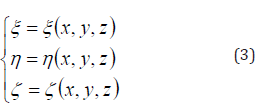
the Navier-Stokes equations can be transformed in generalized coordinates

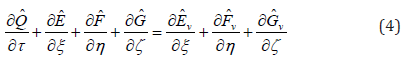
where 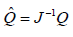and

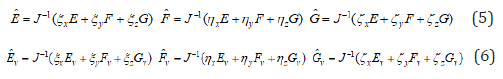
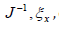etc., are grid metrics 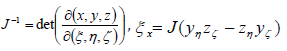, etc.

The domain of the fluid flow with the MVG is illustrated in Figure 1. The grid numbers for the whole system is 137(spanwise) × 192(normal) × 1600(streamwise). Parallel computing is used for this 3D LES [20]. Detail configurations of MVG and the grids can be found in [13].

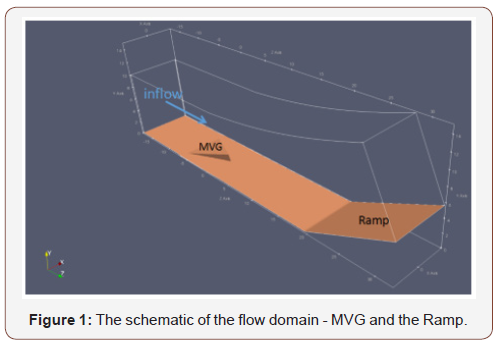
The adiabatic, zero-gradient of pressure and non-slipping conditions are adopted at the wall. To avoid possible wave reflection, the non-reflecting boundary conditions are used on the upper boundary. The boundary conditions at the front and back boundary surfaces in the spanwise direction are treated as the periodic condition. The outflow boundary conditions are specified as a kind of characteristic-based condition, which can handle the outgoing flow without reflection.

To generate the true turbulent inlet, turbulent profiles are obtained from previous DNS simulation and used as the time dependent inflow [21]. After a short range of development, the inflows generated in the upstream of the MVG are fully developed turbulent flows.

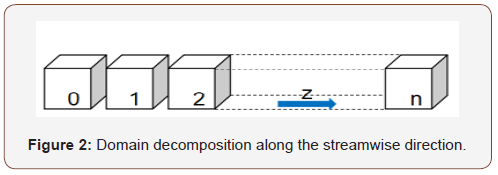
The parallel computation is accomplished through the Message Passing Interface (MPI) together with domain decomposition in the streamwise direction (Figure 2).

In the downstream, there exists a chain of ring-like vortices behind the trailing-edge of MVG. The mechanism of these ring-like vortices was investigated both numerically and analytically [14,15]. The boundary layer shed from the MVG causes momentum deficit. The momentum deficit forms a cylindrical high-shear (HS) layer behind the MVG. The HS layer has inflection surfaces which cause Kelvin-Helmholtz (KH) like instability which generates the ring-like vortices [15]. The existence of the ring-like vortices was verified by Lu’s and Sun’s experiments [13] recently.

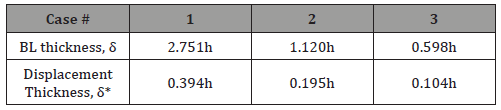
In this work, three simulations are conducted with the different turbulent inflows described above. The boundary layer thicknesses of the inflows obtained in this study are given in Table 1. The shape factors of the boundary layers in front of MVG are 1.33, 1.42, 1.46 respectively, which indicate that the inflows evolve to fully developed turbulent flows. The vortex structures around the MVG in all the three cases are given in Figure 3. Ring-like vortical structure is observed in all cases.

Table 1: flow parameters of the three inlet flows (h is the height of MVG).

To visualize the vortex structures in the field, the λ₂ method [22,23] is used to capture the iso-surfaces of vortices. In this method, λ₂ is the second eigenvalue of the 3 × 3 matrix comprised of velocity gradient, i.e.,

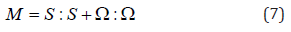
where the 3 × 3 tensors

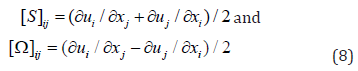
Once the ring-like vortices are generated, they will be continuously distorted and enlarged due to complicated interaction within the boundary layer. Although the difference among the turbulent inflows does not give different mechanisms on the generation of the ring-like vortices [16], the ring-like vortex structures are significantly influenced when they travel to the ramp corner. Figure 3 shows the ring-like vortex structures at the ramp’s corner in the three cases. It shows that the ring-like vortices line up regularly when the boundary layer thickness of inflow is smaller. With smaller inflow boundary layer thickness, there is less distortion applied on the vortex structure so that the ring-like vortices are relatively regular.

Figure 4 also shows that the ring-like vortices are much stronger when they travel to the ramp corner where involves the interaction with the ramp shock. It is normal since less interaction with the lower boundary layer has made the ring-like vortices in case 3 less distorted and remain more stronger. In [12] we already showed that when strong ring-like vortex penetrate the shock wave, the shock wave will be cut off at the location where it meets the ring-like vortex. Although the heights of the ring-like vortices in the three cases are almost the same at the ramp corner, the more regular and stronger ring-like vortices have more ability to reduce the ramp shock.

When the ring-like vortices travel downstream, they will eventually interact with the ramp shock wave. The influence of interaction on ring-like vortices and ramp shock wave were investigated carefully. In the three cases, the ring-like vortical structures are quite robust. They never break down during the interaction. Moreover, they are influenced marginally by the strong shock wave. The interaction is a smooth process to the ring-like vortex structure which is generated by MVG.

However, the 3D ramp shock wave in every case is blurred at the ramp corner substantially. During the interaction with ring-like vortices, the ramp shock wave is badly distorted. In Figure 5, we can see that the quantity of the shock wave is reduced substantially at the region where the interaction happens. The upper part of the shock wave keeps well in the shape. However, the bottom part suffers severe interaction. With the existence of ring-like vortices at upper boundary layer, the separation is reduced due to the interaction.

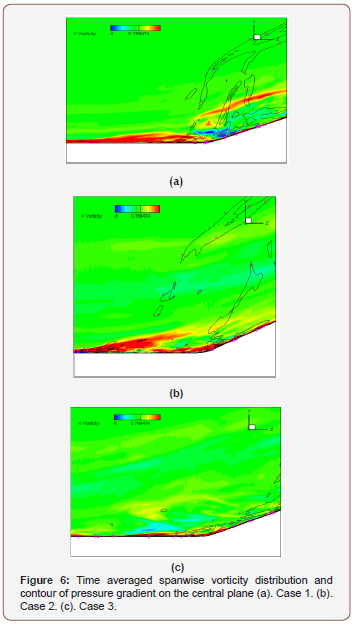
The different turbulent inflows with different boundary layer thickness do bring difference on the interaction between the ringlike vortices and the ramp shock. With lower inflow boundary layer thickness (or relative higher MVG), the ramp shock wave is more reduced by the ring-like vortices. In Figure 6, the time averaged spanwise vorticity distributions and the contour of pressure gradient on the central spanwise plane(x=0) from all the 3 cases are given. The ramp shock wave can be captured by those contour lines of pressure gradient. It can be found that in case 3, the shock wave is almost eliminated at the corner. As a result, there will be less resistance to the separation induced by the ramp shock and the separation zone at the ramp’s corner in case 3 is reduced the most.

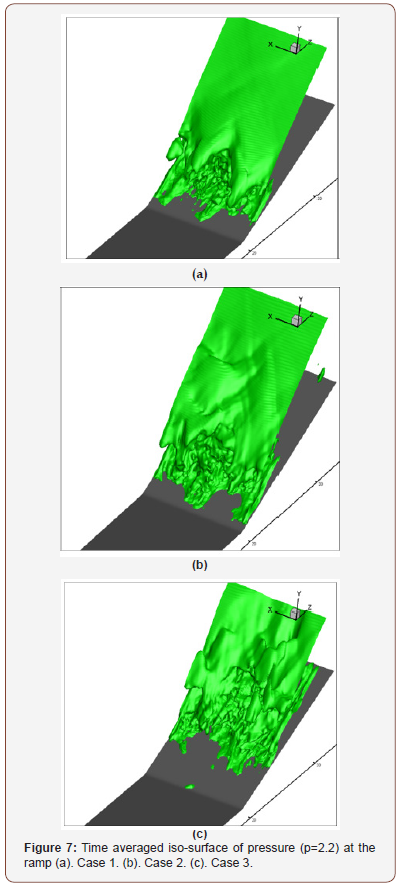
Figure 7 gives the iso-surface of pressure at p=2.2 from the time averaged data of the cases. In Figure 6a, it shows clearly that the ramp’s shock wave is badly distorted and reduced where the interaction with ring-like vortices happens. Furthermore, when the boundary layer thickness of the inflow is lower, the ramp shock wave is more distorted and weakened.

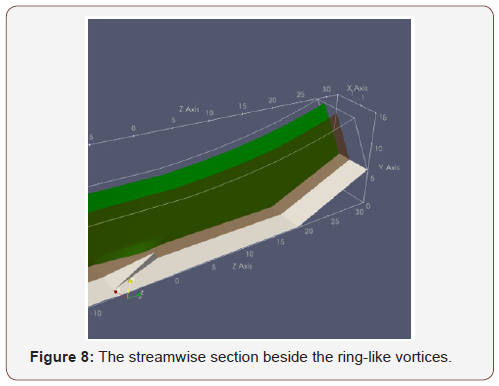
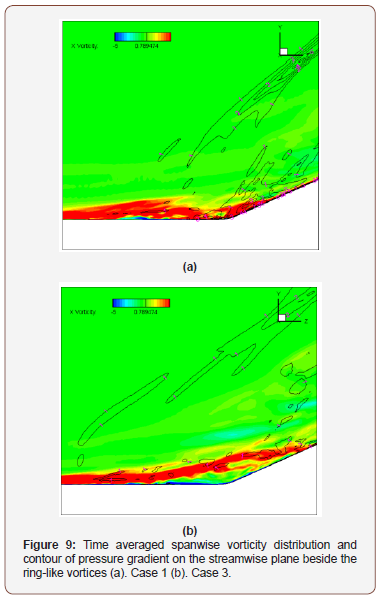
For comparison, time averaged spanwise vorticity distributions and contour of pressure gradient on the streamwise plane beside the ring-like vortices (see Figure 8, the plane in green) of case 1 and case 3 are given in Figure 9. On this streamwise plane, without the interaction between ring-like vortices and shock wave, the shock wave in case 3 is less distorted and the separation zone becomes larger than that in case 1. It’s normal for the larger separation zone in case 3 on that plane since the inlet turbulence intensity is lower. However, it strongly emphasized the role of ring-like vortices on the flow separation reduction in the MVG controlled supersonic ramp flow. With lower inflow boundary layer thickness, the ring-like vortices will be less distorted and thus become stronger when they travel to the ramp corner. The stronger and more regular ring-like vortices have more potential to eliminate the ramp shock wave and reduce the corresponding flow separation induced by the shock wave.

LES (large eddy simulation) is conducted on the MVG controlled supersonic ramp flow under the influence of different inflow conditions. Three turbulent inflows with different boundary layer thickness are generated in front of the MVG. The different inflow conditions do not influence the mechanism of the generation of vortical structures in downstream of MVG but have significant influences on the topology and intensity of the ring-like vortical structure generated by MVG. More important, it is found that the interaction between ring-like vortices and the shock wave at the ramp corner which controls the boundary layer separation is also influenced. With lower boundary layer, the ring-like vortices are less distorted and remain stronger when they propagate to the ramp shock wave. The stronger ring-like vortices thus have more capability to eliminate or distort the strong ramp shock wave. Accordingly, the induced separation zone is more reduced.

This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562.

The authors declare that they have no conflict of interest.

1. in JC (2002) Review of Research on Low-Profile Vortex Generators to Control Boundary-Layer Separation. Progress in Aerospace Sciences 38(4-5): 389-420.
2. Ashill PR, Fulker JL, Hackett KC (2005) A Review of Recent Developments in Flow Control. The Aeronautical Journal 109(1095): 205-232.
3. Dussauge JP, Dupont P, Debieve JF (2006) Unsteadiness in Shock Wave Boundary Layer Interaction with Separation. Aerospace Science and Technology 10(2): 85-91.
4. Estruch Samper D, Vanstone L, Hillier R, Ganapathisubramani B (2015) Micro vortex generator control of axisymmetric high-speed laminar boundary layer separation. Shock Waves 25(5): 521-533.
5. Babinsky H, Li Y, Ford CWP (2009) Microramp Control of Supersonic Oblique Shock-Wave/Boundary-Layer Interactions. AIAA J 47(3): 668- 675.
6. Zhang B, Zhao Q, Xiang X, Xu J (2015) An improved micro-vortex generator in supersonic flows. Aerospace Science and Technology 47: 210–215.
7. Saad MR, Zare Behtash H, Che Idris A, Kontis K (2012) Micro-Ramps for Hypersonic Flow Control. Micromachines 3(2): 364-378.
8. Jeong J, Hussain F (2006) On the identification of a vortex. Journal of Fluid Mechanics 285: 69-94.
9. Tufo HM, Fischer PF, Papka ME, Blom K (1999) Numerical simulation and immersive visualization of hairpin vortices. (Argonne National Lab, IL (US).
10. Li Q, liu C (2010) in 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Aerospace Sciences Meetings (American Institute of Aeronautics and Astronautics).
11. Heinbockel JH (1996) Introduction to Tensor Calculus and Continuum Mechanics.
12. Luo H, Bewley TR (2004) On the contravariant form of the Navier–Stokes equations in time-dependent curvilinear coordinate systems. Journal of Computational Physics 199: 355-375.
13. Yonghua Yan, Qin li, Chaoqun Liu, Adam Pierce, Frank Lu (2012) Numerical Discovery and Experimental Confirmation of Vortex Ring Generation by Microramp Vortex Generator. Applied Mathematical Modelling 36(11): 5700–5708.
14. Yan Y, Liu C (2013) Study on the Initial Evolution of Ring-like Vortices Generated by MVG. CEAS Aeronautical Journal 4(4): 433-442.
15. Yan Y, Liu C (2013) Shear Layer Stability Analysis in Boundary Layer Transition and MVG controlled Ramp Flow. AIAA paper, pp. 1-12.
16. Yan Y, Liu C (2014) Study on the Ring-like Vortical Structure in MVG Controlled Supersonic Ramp Flow with Different Inflow Conditions. Aerospace Science and Technology 35: 106-115.
17. Yonghua Yan, Caixia Chen, Ping Lu, Chaoqun Liu (2013) Study on Shock Wave-Vortex Ring Interaction by the Micro Vortex Generator Controlled Ramp Flow with Turbulent Inflow. Aerospace Science and Technology 30(1): 226–231.
18. Weirs VG, Candler GV (1997) Optimization of weighted ENO schemes for DNS of compressible turbulence. AIAA Paper, pp. 528-538.
19. Sutherland W (1893) LII. The viscosity of gases and molecular force. The London, Edinburgh, and Dublin Philosophical Magazin and Journal of Science 36(223): 507-531.
20. John Towns, Timothy Cockerill, Maytal Dhana, Ian Foster, Kelly Gaither et al. (2014) XSEDE: Accelerating Scientific Discovery. Computing in Science & Engineering 16(5): 62-74.
21. Yonghua Yan, Jie Tang, Chaoqun Liu, Fan Yang (2016) DNS Study on the Formation of Lambda Rotational Core and the Role of TS Wave in Boundary Layer Transition. Journal of Turbulence 17(6): 572-601.
22. Guarini SE, Moser RD, Shariff K, Wray A (2000) Direct numerical simulation of a supersonic turbulent boundary layer at Mach 2.5. Journal of Fluid Mechanics 414(1): 1-33.
23. Yinlin Dong, Yonghua Yan, Chaoqun Liu (2016) New visualization method for vortex structure in turbulence by lambda2 and vortex filaments. Applied Mathematical Modelling 40(1): 500–509.