 Research Article
Research Article
In-Plane Free Vibration of Functionally Graded Rectangular Plates with Elastic Restraint
Changjian Ji1, Linquan Yao1, Jiping Shen*1, Tonghao Hu1 and Cheng Li1
1School of Rail Transportation, Soochow University, China
Jiping Shen, School of Rail Transportation, Soochow University, Suzhou 215131, China.
Received Date: May 08, 2019; Published Date: May 17, 2019
Abstract
The in-plane free vibration of a rectangular plate made of functional graded materials (FGM) is studied based on the two-dimensional linear elasticity theory. The material parameters of FGM rectangular plates are assumed to vary along with the length and width directions according to an exponential law. The governing equation of motion for the FGM rectangular plate is derived using the D’Alembert principle. Subsequently, the equation of motion is solved by the Differential Quadrature Method (DQM), and the natural frequencies for in-plane free vibration of FGM rectangular plate are obtained accordingly. The effects of gradient index, length-width ratio and stiffness of elastic boundary on the natural frequency of FGM rectangular plates are discussed, and the modes for in-plane free vibration are provided.
Keywords:Functionally graded rectangular plates; Elastic restraint; In-plane free vibration; Differential Quadrature Method
Introduction
The vibration and stability of engineering structures play significant roles in structural mechanics. The related research on free vibration, forced vibration, dynamical buckling and stability responses is one of the most important subjects in engineering. The one-dimensional structures, e.g. strings, rods, beams, have been studied sufficiently, especially in recent years [1-5]. The research results provide important reference for the analysis and design of one-dimensional engineering structures including the traveling strings, beams, viscoelastic belts and so on [1-5]. On the other hand, for two-dimensional plate structures, the free vibrations include the out-of-plane vibration (or called transverse vibration) and in-plane vibration, in which the out-of-plane vibration plays a dominant role in energy conversion due to its good coupling properties between frequency band and sound field. Many investigators have carried out a lot of research work on the out-of-plane vibration of plates using different methods. However, more and more experiments have proved that besides the out-of-plane vibration, the in-plane vibration acting as a high frequency component also affects the energy conversion [6]. Therefore, it is also indispensable to study the in-plane vibration of plate structures, and it has attracted much research attention [7-28].
For examples, Kobayashi et al. [7] researched the in-plane vibration behavior of rectangular plate by Ritz method. The inplane vibration frequencies of rectangular plate under different boundary conditions were solved. Moreover, four modal forms were defined according to the order of power series, and the modal characteristics of rectangular plate under different support conditions were analyzed. Gutierrez and Laura [8] studied the in-plane vibration characteristic of rectangular plate with normal elastic constraints by Ritz method. It was assumed that the displacement of in-plane vibration is the superposition of triangular function modes, and the effects of elastic constraints stiffness on the frequency were discussed. Based on thin plate theory and hysteretic damping model, Farag and Pan [9] investigated the resonant characteristics for the in-plane vibration behavior of finite flat plates. The mode shapes of the inplane vibration were depicted for frequencies below and above the first resonance frequency. On this basis, Farag and Pan [10] analyzed the propagation characteristics of in-plane waves, considering the longitudinal and shear waves. The frequency bands for attenuation and propagation of the waves are identified. Based on Kantorovich- Krylov variational method, Wang and Wereley [11] analyzed the in-plane free vibration characteristics and modal characteristics of rectangular plates under three boundary conditions. The modal response functions of rectangular plates under in-plane excitation are given, and the modal characteristics of rectangular plates are discussed. Xing and Liu [18] used the direct separation of variables method to obtain the exact solutions for the free inplane vibrations of rectangular plates under all classical boundary conditions. The frequency and modal characteristics of rectangular plates are discussed, and the problems of frequency loss and repetition are solved. A Ritz method using a set of trigonometric functions is developed to obtain accurate in-plane modal properties of rectangular plates with arbitrary non-uniform elastic edge restraints [21].
All the above papers are concerned with in-plane vibration of rectangular plates with uniform materials. However, there are also many studies on in-plane vibration of rectangular plates with inhomogeneous materials [22-28]. Gorman [22] obtained the accurate solutions analytical type solutions are obtained for the free in-plane vibration frequencies and mode shapes of fully clamped orthotropic rectangular plates by the method of superposition. Based on Reddy’s third-order shear deformation theory, Hosseini Hashemi et al. [23] solved the exact analytical approach for in-plane and out-of-plane free vibration analysis of thick laminated transversely isotropic plates. The in-plane and out-of-plane deformed mode shapes are plotted for different boundary conditions. Shi et al. [25] studied the free in-plane vibration analysis of orthotropic rectangular plates with nonuniform boundary conditions and internal line supports using a modified Fourier solution. Rostami and Ranji [26] provided the results for in-plane vibrations of rotating orthotropic cantilever plates. The equations of motion are derived by Hamilton’s principle and solved by the Extended Kantorovich Method (EKM). The effects of the dimensionless parameters on the natural frequency were investigated, and the resonant frequencies and tune speeds were also discussed. Papkov [27] obtained a new method for in-plane free vibration analysis of rectangular orthotropic plate under the completely clamped or completely free boundary condition. The boundary value problem was assumed to essentially reduce to infinite systems of linear algebraic equations. The accuracy and computational efficiency of the method were demonstrated by examples.
In recent years, a new type of FGM composite material has emerged. FGM has excellent physical and chemical properties, and it has been extensively studied. Therefore, this paper presents the inplane free vibration behaviors of FGM rectangular plates with elastic restraints. It is assumed that the material physical parameters vary along with two directions according to the exponential law. The equation of motion is solved by DQM, and the natural frequencies are thus obtained. Through numerical examples, the effects of gradient index, length-width ratio, and stiffness of elastic boundary on in-plane free vibration frequency and modes are discussed in detail.
Mechanical Model and Governing Equations
For an in-plane functionally graded rectangular plates as shown in Figure 1, the length and width of thin plates are a and b respectively, and the thickness is d (much less than a and b). Springs are evenly distributed along the normal and tangent directions on the boundary of rectangular plates, and the stiffness of springs are n K and Kτ respectively. The subscript n represents the normal direction, and the subscript τ represents the tangent direction.
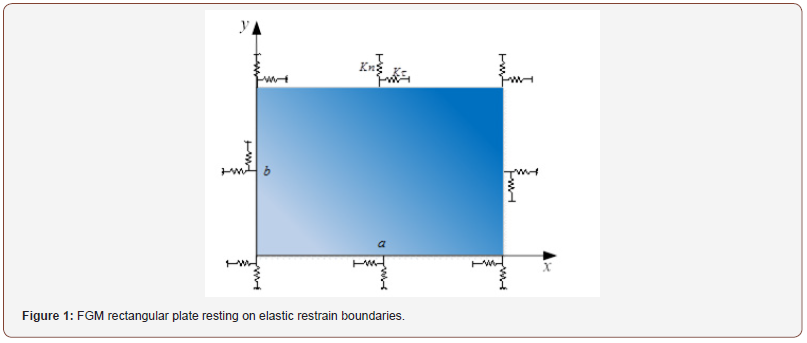
The material parameters of functionally graded plates are assumed to vary along the length and width direction according to exponential law, and the material parameters can be described by
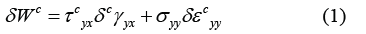
where P(x, y) represents the modulus of elasticity E and density ρ . 0 P stands for the material parameters at (0, 0), and 1 P stands for the material parameters at (a, b). α and β are the gradient index.
According to the two-dimensional linear elasticity theory, the geometric equations of rectangular plate can be expressed as
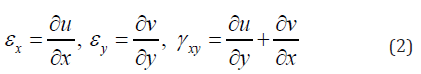
Where ( , , ) x u = u x y t and ( , , ) y u = v x y t stand for the transverse and longitudinal displacement component of FGM rectangular plate, respectively. xx ε and yy ε represent the normal strain in x and y directions, respectively. xy γ is the shear strain.
The constitutive equation of functionally graded rectangular plates is
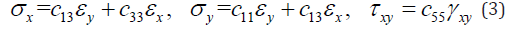
where x σ and y σ represent the normal stress in x and y directions, respectively. xy τ is the shear stress. ij c represents the elastic modulus coefficients, and these coefficients are functions of position (x, y).
According to D’Alembert principle, the equations of motion for in-plane vibration of rectangular plates can be obtained as

where u and v represent the second derivative of displacement component u and v for time, ρ is density of rectangular plates.
For rectangular plates with quadrilateral elastic constraints, the boundary conditions are as follows
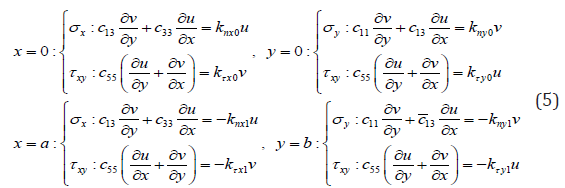
where nx0 k and x0 kτ represent the stiffness coefficients at x=0, ny0 k and y0 kτ represent the stiffness coefficients at y=0, nx1 k and x1 kτ represent the stiffness coefficients at x=a, ny1 k and y1 kτ represent the stiffness coefficients at y=b.
By introducing the following non-dimensional terms:
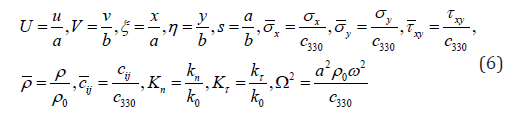
in which 0 330 k = c b , i, j =1,3,5 . 330 c and 0 ρ represent the elastic modulus and density of materials at (0,0), respectively. Ω stands for the non-dimensional natural frequency.
Substituting Eq. (6) into Eq. (4), the non-dimensional equations of motion can be established as
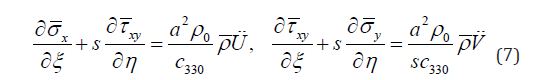
Since the mode of FGM plate is harmonic to time, the displacement can be assumed to be as
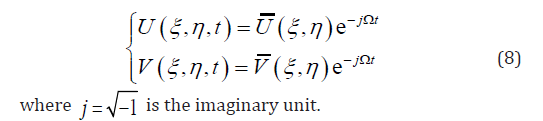
Substituting Eq. (8) into Eq. (7), the non-dimensional characteristic equations of in-plane free vibration of functionally graded rectangular plates are obtained as
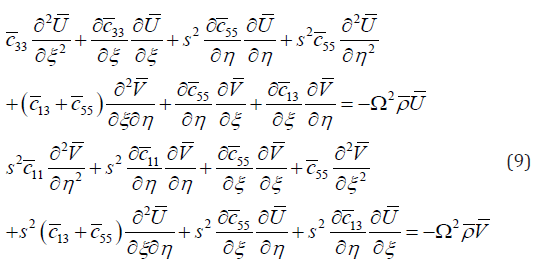
Substituting Eqs. (6) and (8) into Eq. (5), the boundary conditions expressed by mode shapes can be expressed as
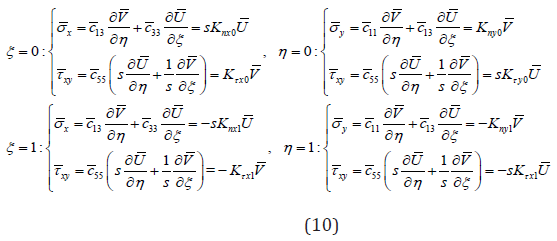
When n K and Kτ take different values, different boundary conditions can be obtained as
Clamped boundary(C): nx0 x0 K Kτ = = ∞ , Free boundary(F): 0 0 0 nx x K Kτ = = ,
Special boundary 1(S1):Knx0 =0, Kτx0 = ∞ ,
Special boundary 2(S2):Knx0 =∞, Kτx0 = 0 ,
As can be seen, equation (9) is a second order coupled differential equation with variable coefficients. It is very difficult to solve it directly, so the differential quadrature method (DQM) is used to solve it.
Method of Solution
In this section, the DQM is used to solve the equations. In DQM, we can express the derivative of a function at a given point as a weighted linear summation of the values of the function at all the points in the domain [29]. Therefore, the differential equation can be transformed into a set of algebraic equations expressed by the value of the function at the node. When using this method, there are two questions to be determined:
Selection of node
A well accepted kind of sampling points in the DQM is the socalled Gauss-Lobatto-Chebyshev points [21]:
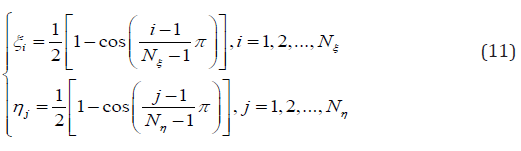
where Nξ and Nη represent the number of nodes selected in the direction of ξ and η , respectively.
Determination of weight coefficient
By introducing Lagrange interpolation function, the weight coefficient of first derivative for ξ is expressed as [30]
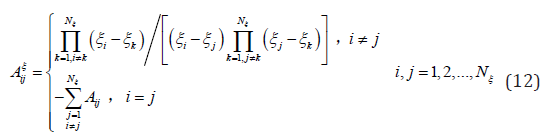
According to formula (12), the weight coefficients of second derivative can be obtained as
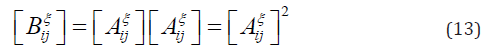
The weight coefficient for η is similar to that for ξ , and the specific expression is omitted.
Using DQM to discretize the equations of motion (9), the discretized equations of motion are obtained as follows
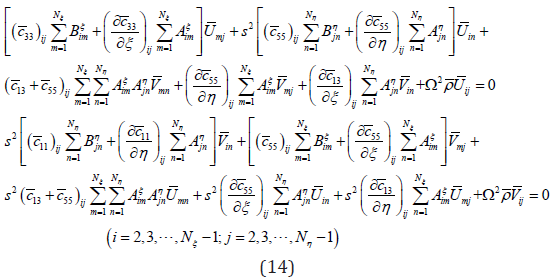
Using DQM to discretize the boundary conditions (10), the discretized boundary conditions are obtained as follows
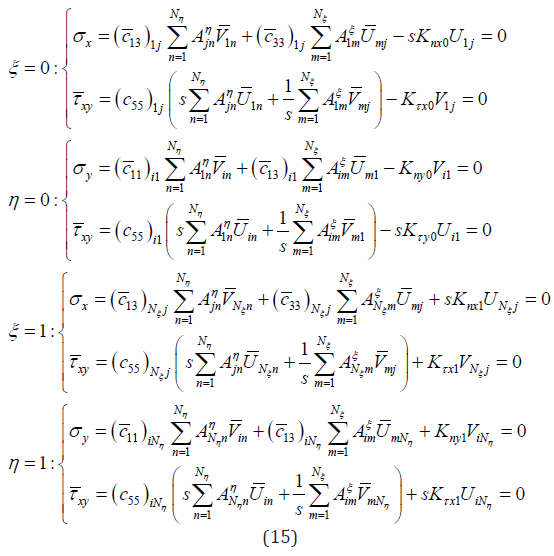
Combining differential equation (14) and boundary condition (15), the matrix form of motion equations for free vibration of rectangular plate with elastically constrained boundary is expressed as

where bb K and bd K represent the stiffness matrix of motion equations, db K and dd K stand for the stiffness matrix of boundary conditions. b q and d q represent the Column vectors of nodal displacements at the interior and boundary, respectively, expressed as
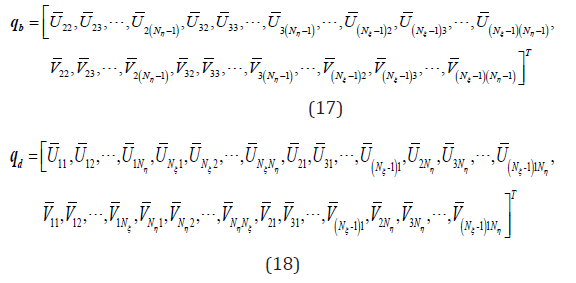
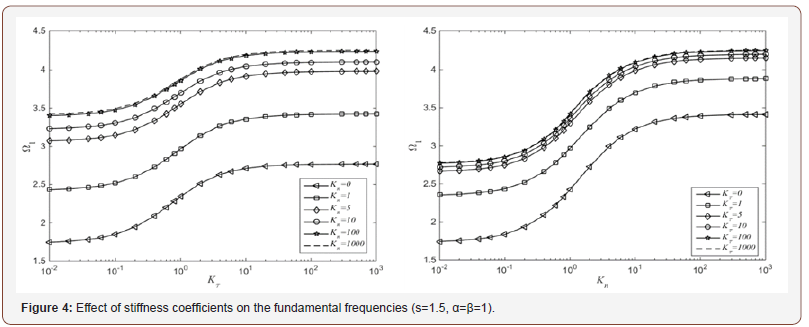
By eliminating the d q in formula (16), the eigenvalue equation of free vibration for a functionally graded rectangular plate can be obtained as
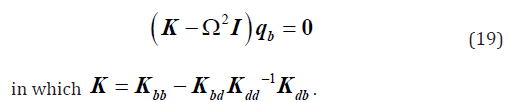
Numerical Examples and Analysis
Frequency characteristics for in-plane free vibration of FGM rectangular plate
In this section, the frequency characteristics for in-plane free vibration of FGM rectangular plate are studied. In the examples, it is assumed that the material at coordinate (0, 0) is pure metal Ti-6Al-4V, and the material at coordinates (a, b) is pure ceramics ZrO2. Their physical parameters are 0 0 E =132.2Gpa, μ = 0.3, 3 3 0 1 1 1 ρ = 3657kg/m , E =122.7Gpa, μ = 0.288, ρ = 4420kg/m . The number of nodes Nξ and Nη are assumed to be 17.
Effect of gradient indexes on frequency: Figure 2 shows the effect of gradient indexes α and β on the fundamental frequency 1 Ω of FGM rectangular plate under various boundary conditions, in which the length-width ratio s is equal to 1 and the gradient indexes vary from 0 to 4. In Figure 2(a), when α and β are both equal to zero, the first-order frequency 1 Ω of FGM rectangular plate under the four-sided clamped boundary condition (C-C-C-C) is 3.55. In reference [2], the analytical solution of the first-order frequency is equal to 3.51. It can be seen that DQM has high accuracy and good astringency and stability. From Figure 2(a) to Figure 2(i), it can be seen that with the increase of gradient indexes, the fundamental frequency increases gradually and then tends to the constant.
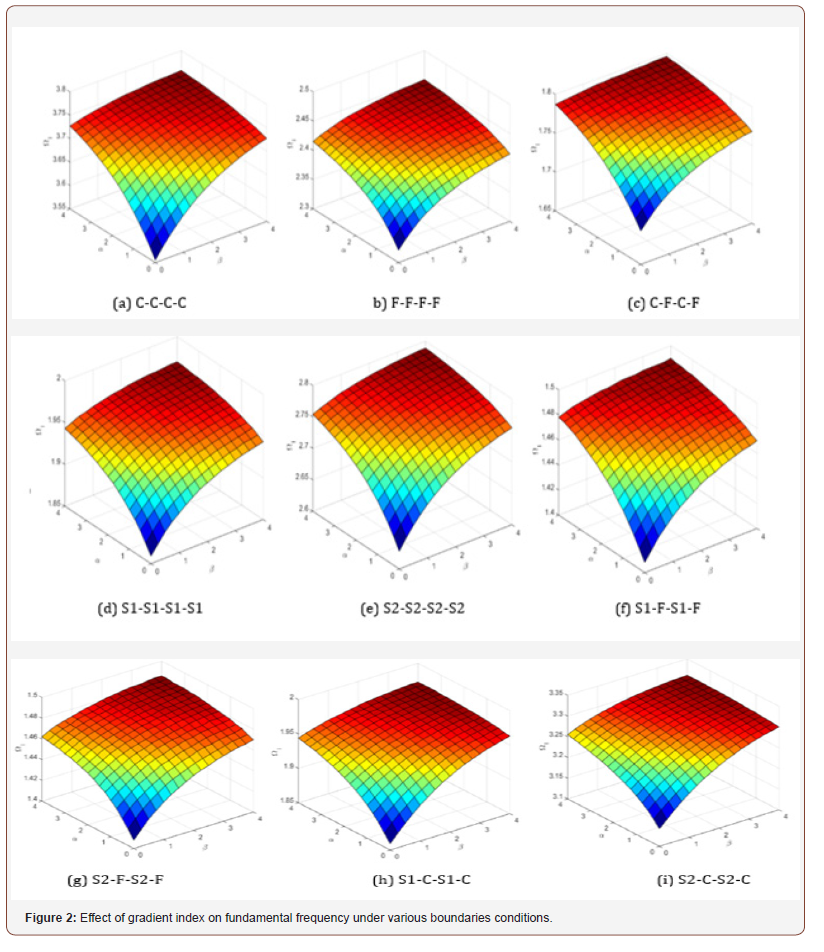
Effect of length-width ratio on fundamental frequency: Figure 3 shows the effect of length-width ratio s on the fundamental frequency 1 Ω of FGM rectangular plate under various boundary conditions, in which the gradient indexes are assumed to be α = β =1 and length-width ratio s varies from 1 to 3. It can be seen from Fig. 3 that the influence of length-width ratio on fundamental frequency plate is different for different boundary conditions. In detail, The fundamental frequencies of FGM rectangular plate under C-C-C-C and S1-C-S1-C boundary conditions increase with the increase of length-width ratio, while those under C-F-S1-F, C-FS2- F, C-F-C-F and S1-F-S1-F boundary conditions decrease with the increase of length-width ratio, and those under S1-S1-S1-S1 boundary condition remain unchanged with the increase of lengthwidth ratio. Therefore, we should pay particular attention to the specific boundary constraints when designing an FGM rectangular plate especially when the in-plane vibration cannot be neglected.
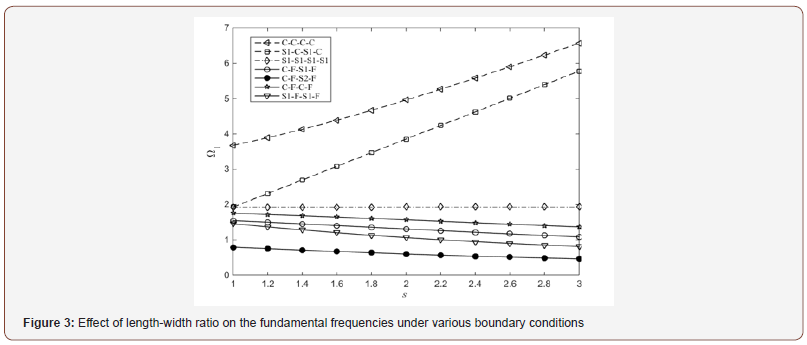
Effect of stiffness of elastic boundary on frequency: Figure 4 shows the relationship between the stiffness coefficient and the fundamental frequency under a special boundary condition (S1-S1-S2-S2). It is assumed that the normal stiffness coefficient nx0 K and ny0 K are both expressed as n K , the tangential stiffness coefficient x1 Kτ and y1 Kτ are both expressed as Kτ , and other stiffness coefficients 1 1 0 0 , , , nx ny x y K K K K τ τ are equal to ∞ . n K and Kτ vary from 0.01 to 103, and logarithmic coordinates are used in abscissa. Figure 4(a) shows the effect of tangential stiffness coefficient Kτ on the fundamental frequencies with different normal stiffness coefficients. It can be seen that with the increase of tangential stiffness coefficient, the fundamental frequency increases, especially when Kτ varies from 1 to 10. From another angle, increasing the n K leads to the increase of 1 Ω .
Figure 4(b) shows the effect of normal stiffness coefficient n K on the fundamental frequencies with different tangential stiffness coefficients. It can be seen that the effect of normal stiffness coefficient n K on the fundamental frequencies is the same as the effect of tangential stiffness coefficient Kτ on the fundamental frequencies. However, comparing Figures 4(a) & 4(b), it can be seen that the influence of normal stiffness coefficients on fundamental frequency is more remarkable than that of tangential stiffness coefficients.
Modal characteristics for in-plane free vibration of FGM rectangular plate
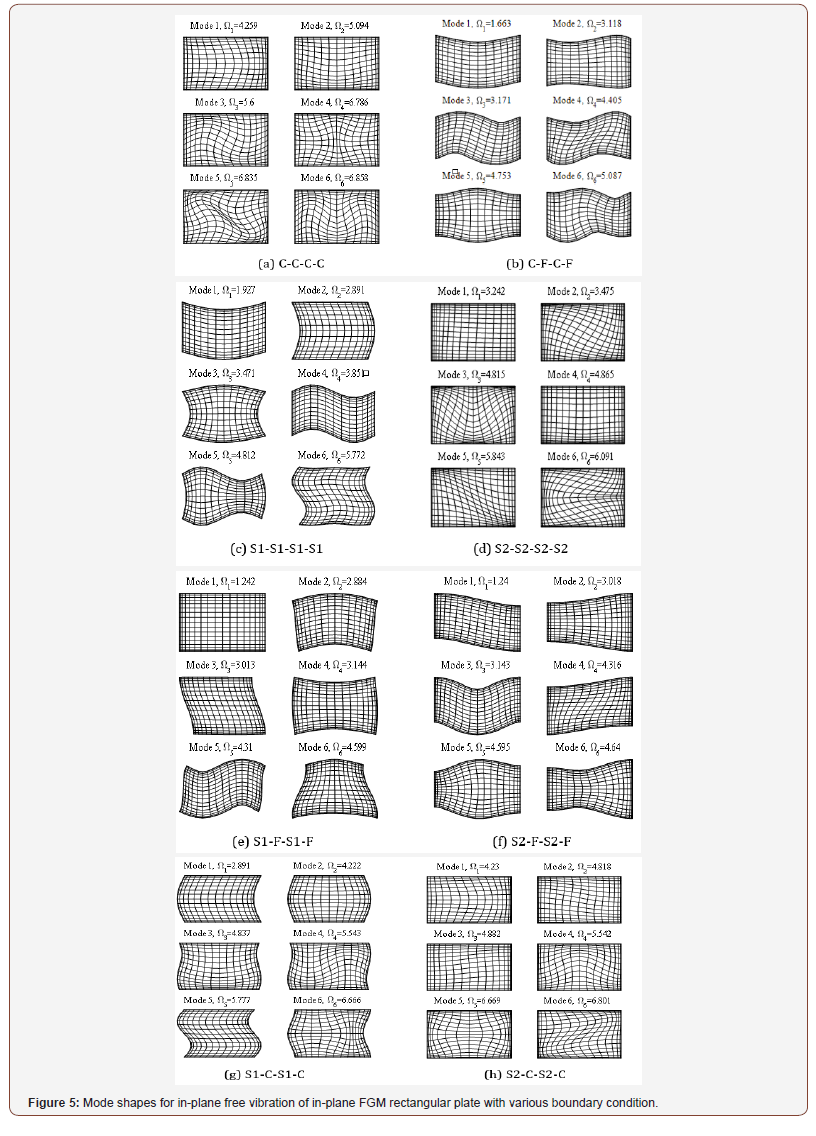
In order to reveal the in-plane vibration mechanism of FGM rectangular plates, it is necessary to study the modal characteristics of them. Figure 5 shows the first six order modal diagrams of rectangular plates under various boundary conditions when s is equal to 1.5, α and β are both equal to 1. From Figure 5, it can be seen that the vibration frequency of four-sided clamped(C-C-C-C) FGM plates is the largest, and the vibration frequency of S1-F-S1-F FGM plates is the smallest. Moreover, for the clamped boundary, symmetric or antisymmetric modes will appear at the interior points of FGM rectangular plate, and this property is also suitable for the S1 and S2 boundaries. For the free boundary, symmetric or antisymmetric modes will appear at the interior points and boundaries of FGM rectangular plate, and coupled vibration occurs at normal and tangential directions.
Conclusion
The in-plane free vibration of FGM rectangular plate is studied based on the two-dimensional linear elasticity theory. The equation of motion is established, and the natural frequencies are determined. The variations of natural frequencies concerning the gradient index, length-width ratio and stiffness of elastic boundary are obtained. It is found that DQM has better accuracy in analyzing the in-plane vibration of FGM rectangular plates. Moreover, with the increase of gradient index, the fundamental frequency increases gradually and then tends to a constant, the influence of length-width ratio on fundamental frequency is different for different boundary conditions, and with the increase of stiffness coefficient, the fundamental frequency increases. Finally, the modal characteristics of FGM rectangular plates are studied. It is found that symmetric or antisymmetric modes appear at the interior points of FGM rectangular plate for the clamped, S1 and S2 boundaries. For the free boundary, symmetric or antisymmetric modes appear at the interior points and boundaries, and coupled vibration occurs at normal and tangential directions. According to the above characteristics, the frequency required in a certain range can be obtained by changing these parameters of FGM rectangular plates. Therefore, this study can provide a reference for the twodimensional FGM rectangular plate structural engineering where the in-plane free vibration plays a remarkable role.
Acknowledgement
This work is supported by the National Natural Science Foundation of China (No. 11572210) and the Postgraduate Research and Practice Innovation Program of Jiangsu province (No. KYCX17_1983).
Conflict of Interest
No conflict of interest.
References
- Chen LQ, Zhang GC, Ding H (2015) Internal resonance in forced vibration of coupled cantilevers subjected to magnetic interaction. Journal of Vibration and Control 354: 196-218.
- Mao XY, Ding H, Chen LQ (2017) Dynamics of a super-critically axially moving beam with parametric and forced resonance. Nonlinear Dynamics 89(2): 1475–1487.
- Ding H, Dowell EH, Chen LQ (2018) Transmissibility of bending vibration of an elastic beam. AMSE Journal of Vibration and Acoustics 140(3): 031007.
- Ding H, Lim CW, Chen LQ (2018) Nonlinear vibration of a traveling belt with non-homogeneous boundaries. Journal of Sound and Vibration 424(23): 78-93.
- Ding H, Lu ZQ, Chen LQ (2019) Nonlinear isolation of transverse vibration of pre-pressure beams. Journal of Sound and Vibration 442: 738-751.
- Lyon RH (1986) In-plane Contribution to Structural Noise Transmission. Noise Control Engineering Journal 26(1): 22.
- Kobayashi Y, Yamada G, Honma S (1988) In-plane vibration of pointsupported rectangular plates. Journal of sound and vibration 126(3): 545-549.
- Gutierrez RH, Laura PAA (1989) In-plane vibrations of thin, elastic, rectangular plates elastically restrained against translation along the edges. Journal of sound and vibration 132(3): 512-515.
- Farag NH, Pan J (1998) Free and forced in-plane vibration of rectangular plates. The Journal of the Acoustical Society of America 103(1): 408-413.
- Farag NH, Pan J (1999) Modal characteristics of in-plane vibration of rectangular plates. The Journal of the Acoustical Society of America 105(6): 3295-3310.
- Wang G, Wereley NM (2002) Free in-plane vibration of rectangular plates. AIAA journal 40(5): 953-959.
- Seok J, Tiersten HF, Scarton HA (2004) Free vibrations of rectangular cantilever plates. Part 2: in-plane motion. Journal of sound and vibration 271(1): 147-158.
- Gorman DJ (2004) Free in-plane vibration analysis of rectangular plates by the method of superposition. Journal of Sound and Vibration 272(3): 831-851.
- Gorman DJ (2004) Accurate analytical type solutions for the free inplane vibration of clamped and simply supported rectangular plates. Journal of Sound and Vibration 276(1): 311-333.
- Gorman DJ (2005) Free in-plane vibration analysis of rectangular plates with elastic support normal to the boundaries. Journal of sound and vibration 285(4): 941-966.
- Gorman DJ (2006) Exact solutions for the free in-plane vibration of rectangular plates with two opposite edges simply supported. Journal of Sound and Vibration 294(1): 131-161.
- Du J, Li WL, Jin G, Yang T, Liu Z (2007) An analytical method for the inplane vibration analysis of rectangular plates with elastically restrained edges. Journal of Sound and Vibration 306(3): 908-927.
- Xing YF, Liu B (2009) Exact solutions for the free in-plane vibrations of rectangular plates. International Journal of Mechanical Sciences 51(3): 246-255.
- Chen LQ, Lim CW, Hu QQ, Ding H (2009) Asymptotic analysis of a vibrating cantilever with a nonlinear boundary. Science in China G 59(2): 1414-1422
- Du JT, Liu ZG, Li WL, Zhang XF, Li WF (2010) Free in-plane vibration analysis of rectangular plates with elastically point-supported edges. Journal of Vibration and Acoustics 132(3): 031002.
- Dozio L (2010) Free in-plane vibration analysis of rectangular plates with arbitrary elastic boundaries. Mechanics Research Communications 37(7): 627-635.
- Gorman DJ (2009) Accurate in-plane free vibration analysis of rectangular orthotropic plates. Journal of Sound and Vibration 323(1): 426-443.
- Hosseini Hashemi S, Atashipour SR, Fadaee M (2012) An exact analytical approach for in-plane and out-of-plane free vibration analysis of thick laminated transversely isotropic plates. Archive of Applied Mechanics 82(5): 677-698.
- Ding H (2015) Periodic Responses of a pulley-belt system with one-way clutch under inertia excitation. Journal of Sound and Vibration 353: 308-326.
- Shi DY, Wang QS, Shi XJ, Pang FZ (2015) A series solution for the inplane vibration analysis of orthotropic rectangular plates with non-uniform elastic boundary constraints and internal line supports. Archive of Applied Mechanics 85(1):51-73.
- Rostami H, Ranji AR, Bakhtiari-Nejad F (2016) Free in-plane vibration analysis of rotating rectangular orthotropic cantilever plates. International Journal of Mechanical Sciences 115: 438-456.
- Papkov SO (2016) A new method for analytical solution of inplane free vibration of rectangular orthotropic plates based on the analysis of infinite systems. Journal of Sound and Vibration 369: 228-245.
- ERT CW, MALIK M (1996) Differential quadrature method in computational mechanics: a review. Applied Mechanics Reviews 49(1): 1-28.
- Mao XY, Ding H, Chen LQ (2017) Vibration of flexible structures under nonlinear boundary conditions. ASME Journal of Applied Mechanics 84(11): 111006.
- Zeighampour H, Beni YT (2015) Free vibration analysis of axially functionally graded nanobeam with radius varies along the length based on strain gradient theory. Applied Mathematical Modelling 39(18): 5354-5369.
-
Jiping Shen, Changjian Ji, Linquan Yao, Tonghao Hu, Cheng Li. In-Plane Free Vibration of Functionally Graded Rectangular Plates with Elastic Restraint. Glob J Eng Sci. 2(3): 2019. GJES.MS.ID.000537.
-
Functionally graded rectangular plates, Elastic restraint, In-plane free vibration, Differential Quadrature Method
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






