 Research Article
Research Article
Effect of Boundary Conditions on Buckling Load for Laminated Composite Plates
Osama Mohammed Elmardi Suleiman1*, Mahmoud Yassin Osman2 and Tagelsir Hassan3
1Federal University of Technology, Akure, Nigeria
2Department of Mechanical Engineering, Kassala University, Sudan
1Department of Mechanical Engineering, Omdurman Islamic University, Sudan
Osama Mohammed Elmardi Suleiman, Department of Mechanical Engineering, Nile Valley University, Atbara, River Nile, Sudan.
Received Date: March 27, 2019; Published Date: April 30, 2019
Abstract
It is observed that, for all cases the buckling load increases with the mode number but at different rates depending on whether the plate is simply supported, clamped or clamped – simply supported. The buckling load is a minimum when the plate is simply supported and a maximum when the plate is clamped. Because of the rigidity of clamped boundary condition, the buckling load is higher than in simply supported boundary condition. It is also observed that as the mode number increases, the plate needs additional support.
Keywords: Boundary conditions; Biaxial buckling; Classical laminated plate theory; Finite element; Fortran program; Composite laminated decks plates
Introduction
The objective of this research paper is to present a complete and up to date treatment of uniform cross section rectangular laminated decks plates on buckling. Finite element (FE) method is used for solving governing equations of thin laminated composite plates and their solution using classical laminated plate theory (CLPT). Plates are common structural elements of most engineering structures, including aerospace, automotive, and civil engineering structures, and their study from theoretical and experimental analyses points of view are fundamental to the understanding of the behavior of such structures.
The motivation that led to the carrying out of the present study has come from many years of studying classical laminated plate theory (CLPT) and its analysis by the finite element (FE) method, and also from the fact that there does not exist a publication that contains a detailed coverage of classical laminated plate theory and finite element method in one volume. The present study is an attempt to fulfill the need for a complete treatment of classical laminated theory of plates and its solution by a numerical solution.
The material presented is intended to serve as a basis for a critical study of the fundamentals of elasticity and several branches of solid mechanics including advanced mechanics of materials, theories of plates, composite materials and numerical methods.
Geophysics is the application of physics principles to the study of the Earth. The Earth is comprised of materials that have different physical properties. Geophysical instruments are designed to map spatial variations in the physical properties of the Earth. Geophysicists interpret these measured variations and use them to generate geologic models of varying sophistication. If the subsurface target of interest can be differentiated from the encompassing strata on the basis of contrasting physical properties, the output geologic model can be of great utility to a geotechnical engineer.
The problem of critical buckling loads of laminated composite plates is analyzed and solved using the energy method which is formulated by a finite element model. In that model, four nodded rectangular elements of a plate is considered. Each element has three degrees of freedom at each node. The degrees of freedom are the lateral displacement w, and the rotations ϕ and ψ about the y and x axes respectively.
The effects of lamination scheme on the non – dimensional critical buckling loads of laminated composite plates are investigated.
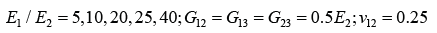
Several numerical methods could be used in this study, but the main ones are finite difference method (FDM), dynamic relaxation coupled with finite difference method (DR) as is shown in references [1-8], and finite element method (FEM).
In the present work, a numerical method known as finite element method (FEM) is used. It is a numerical procedure for obtaining solutions to many of the problems encountered in engineering analysis. It has two primary subdivisions. The first utilizes discrete elements to obtain the joint displacements and member forces of a structural framework. The second uses the continuum elements to obtain approximate solutions to heat transfer, fluid mechanics, and solid mechanics problem. The formulation using the discrete element is referred to as matrix analysis of structures and yields results identical with the classical analysis of structural frameworks. The second approach is the true finite element method. It yields approximate values of the desired parameters at specific points called nodes. A general finite element computers program, however, is capable of solving both types of problems and the name” finite element method” is often used to denote both the discrete element and the continuum element formulations.
The finite element method combines several mathematical concepts to produce a system of linear and non – linear equations. The number of equations is usually very large, anywhere from 20 to 20,000 or more and requires the computational power of the digital computer.
It is impossible to document the exact origin of the finite element method because the basic concepts have evolved over a period of 150 or more years. The method as we know it today is an outgrowth of several papers published in the 1950th that extended the matrix analysis of structures to continuum bodies. The space exploration of the 1960th provided money for basic research, which placed the method of a firm mathematical foundation and stimulated the development of multi-purpose computer programs that implemented the method. The design of airplanes, unmanned drones, missiles, space capsules, and the like, provided application areas.
The finite element method (FEM) is a powerful numerical method, which is used as a computational technique for the solution of differential equations that arise in various fields of engineering and applied sciences. The finite element method is based on the concept that one can replace any continuum by an assemblage of simply shaped elements, called finite elements with well-defined force, displacement, and material relationships. While one may not be able to derive a closed – form solution for the continuum, one can derive approximate solutions for the element assemblage that replaces it. The approximate solutions or approximation functions are often constructed using ideas from interpolation theory, and hence they are also called interpolation functions. For more details refer to References [9-11].
Mathematical Formulations
Introduction
The following assumptions were made in developing the mathematical formulations of laminated plates:
1. All layers behave elastically;
2. Displacements are small compared with the plate thickness;
3. Perfect bonding exists between layers;
4. The laminate is equivalent to a single anisotropic layer;
5. The plate is flat and has a constant thickness;
6. The plate buckles in a vacuum and all kinds of damping are neglected.
Unlike homogeneous plates, where the coordinates are chosen solely based on the plate shape, coordinates for laminated plates should be chosen carefully. There are two main factors for the choice of the coordinate system. The first factor is the shape of the plate. Where rectangular plates will be best represented by the choice of rectangular (i.e. Cartesian) coordinates. It will be relatively easy to represent the boundaries of such plates with coordinates. The second factor is the fiber orientation or orthotropic. If the fibers are set straight within each lamina, then rectangular orthotropic would result. It is possible to set the fibers in a radial and circular fashion, which would result in circular orthotropic. Indeed, the fibers can also be set in elliptical directions, which would result in elliptical orthotropic.
The choice of the coordinate system is of critical importance for laminated plates. This is because plates with rectangular orthotropic could be set on rectangular, triangular, circular or other boundaries. Composite materials with rectangular orthotropic are the most popular, mainly because of their ease in design and manufacturing. The equations that follow are developed for materials with rectangular orthotropic.
Figure 1 shows the geometry of a plate with rectangular orthotropic drawn in the Cartesian coordinates X, Y, and Z or 1, 2, and 3. The parameters used in such a plate are: (1) the length in the X-direction, (a); (2) the length in the Y – direction (i.e. breadth), (b); and (3) the length in the Z – direction (i.e. thickness), (h).
Fundamental equations of elasticity
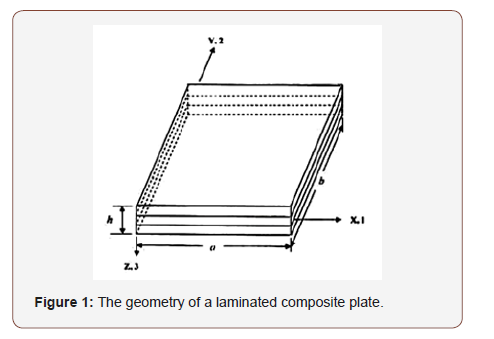
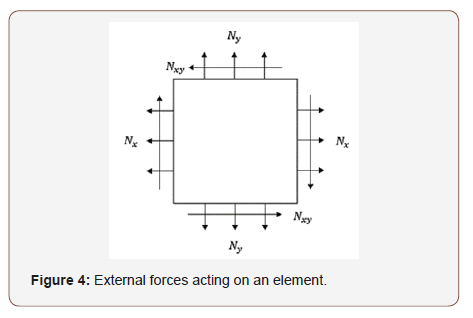
Classical laminated plate theory (CLPT) is selected to formulate the problem. Consider a thin plate of length a, breadth b, and thickness h as shown in Figure 2(a), subjected to in – plane loads Rx, Ry and Rxy as shown in Figure 2(b). The in-plane displacements u(x,y,z) and v(x,y,z) can be expressed in terms of the out of plane displacement w(x,y) as shown below:
The displacements are:

Where , and are mid – plane displacements in the direction of the x, y and z axes respectively; z is the perpendicular distance from mid – plane to the layer plane.
The plate shown in Figure 2(a) is constructed of an arbitrary number of orthotropic layers bonded together as in Figure 3.
The strains are:
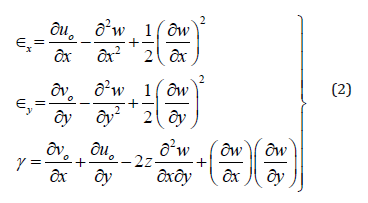
The virtual strains:
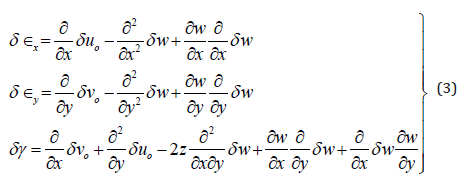
The virtual strain energy:
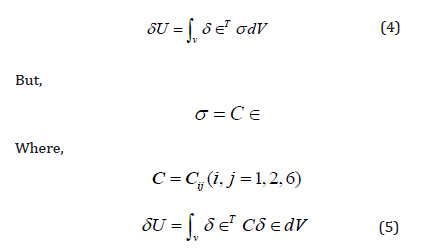
If we neglect the in-plane displacements and and considering only the linear terms in the strain-displacement equations, we write:
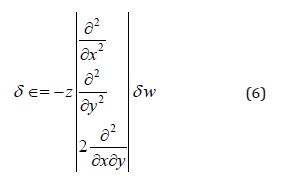
The Numerical Method
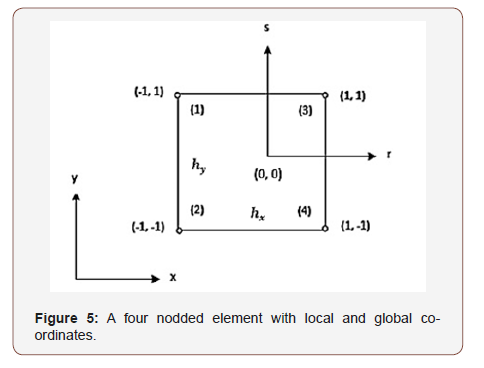
The finite element is used in this analysis as a numerical method to predict the buckling loads and shape modes of buckling of laminated rectangular plates [12,13]. In this method of analysis, four – nodded type of elements is chosen. These elements are the four – nodded bilinear rectangular elements of a plate. Each element has three degrees of freedom at each node. The degrees of freedom are the lateral displacement (w), and the rotations (ϕ) and (ψ) about the (X) and (Y) axes respectively.
The finite element method is formulated by the energy method. The numerical method can be summarized in the following procedures:
• The choice of the element and its shape functions.
• Formulation of finite element model by the energy approach to develop both element stiffness and differential matrices.
• Employment of the principles of non – dimensionality to convert the element matrices to their non – dimensional forms.
• Assembly of both element stiffness and differential matrices to obtain the corresponding global matrices.
• Introduction of boundary conditions as required for the plate edges.
• Suitable software can be used to solve the problem.
• For an n nodded element, and 3 degrees of freedom at each node.
Now express w in terms of the shape functions N (given in Appendix (B)) and nodded displacements , equation (6) can be written as:
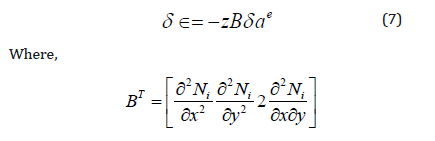
The stress – strain relation is:
σ = C∈
Where C are the material properties which could be written as follows:
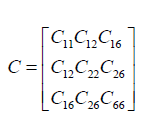
Where are given in Appendix (A).
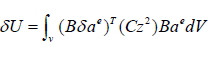
Where V denotes volume.
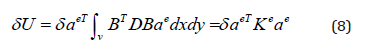
Where
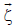 is the bending stiffness, and Ke
is the element stiffness matrix which could be written as follows:
is the bending stiffness, and Ke
is the element stiffness matrix which could be written as follows:
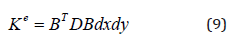
Denoting the nonlinear part of strain by

This can be written as:
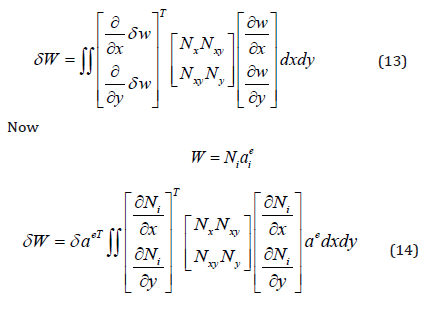
Substitute Px = −Nx , Py = −Ny , Pxy = −Nxy
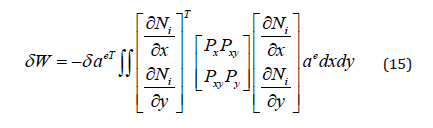
Therefore, equation (15) could be written in the following form:
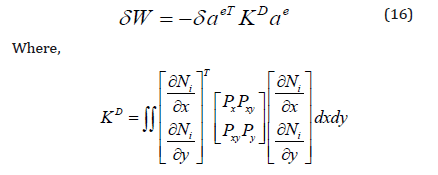
is the differential stiffness matrix known also as geometric stiffness matrix, initial stress matrix, and initial load matrix.
The total energy:
δU +δW = 0 (17)
Since δae is an arbitrary displacement which is not zero, then
Keae − KDae = 0 (18)
Now let us compute the elements stiffness and the differential matrices.
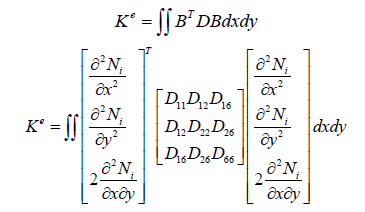
The elements stiffness matrix can be expressed as follows:
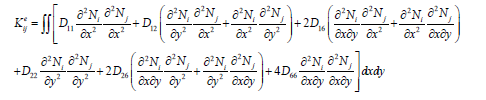
The elements differential stiffness matrix can be expressed as follows;
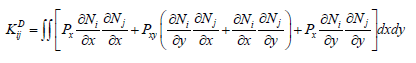
The integrals in equations (19) and (20) are given in Appendix (C).
The shape local co-ordinate for a 4-nodded element is shown below in Figure 5.
The shape functions for the 4-nodded element expressed in global co-ordinates (x,y) are as follows:
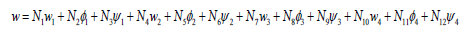
Where,
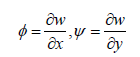
The shape functions in local co – ordinates are as follows:
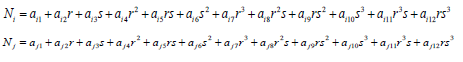
The integrals of the shape functions in local co – ordinates are as follows:

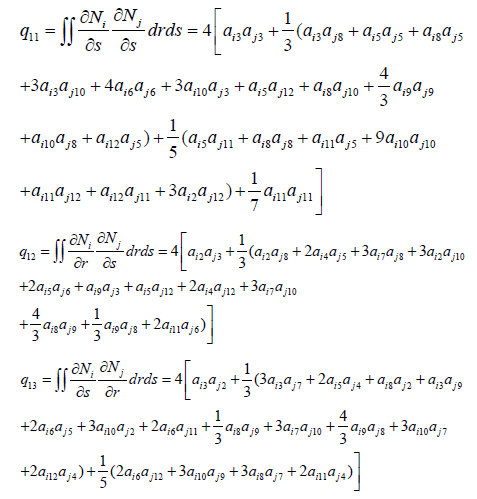
The integrals of the shape functions in global co – ordinates are as follows:
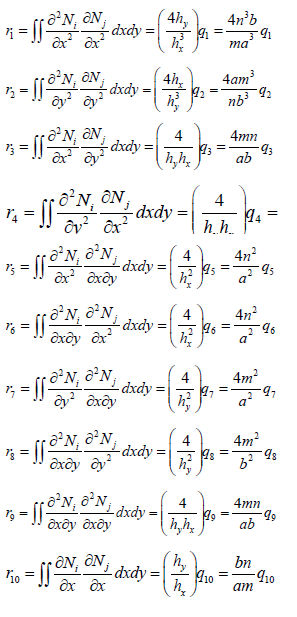
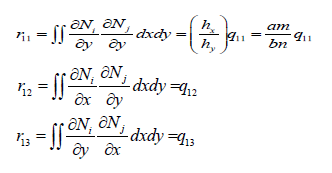
In the previous equations 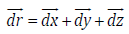 where a and b are the
lengths of the plate along the x – and y – axis respectively. n and m
are the number of elements in the x – and y – directions respectively.
where a and b are the
lengths of the plate along the x – and y – axis respectively. n and m
are the number of elements in the x – and y – directions respectively.
The elements of the stiffness matrix and the differential matrix can be written as follows:
or in the non – dimensional form:
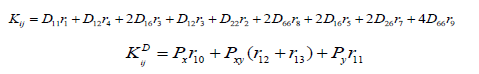
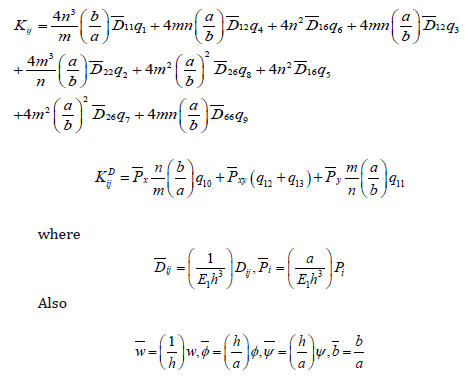
The transformed stiffnesses are as follows:
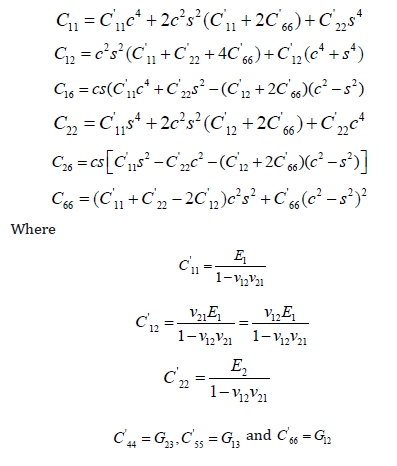
E1 and E2 are the elastic moduli in the direction of the fiber and the transverse directions respectively, v is the Poisson’s ratio. G12, G13, and G23 are the shear moduli in the x – y plane, y – z plane, and x – z plane respectively, and the subscripts 1 and 2 refer to the direction of fiber and the transverse direction respectively.
Effect of Boundary Conditions
The type of boundary support is an important factor in determining the buckling loads of a plate along with other factors such as aspect ratio, modulus ratio, … etc.
Three sets of boundary conditions, namely simply – simply supported (SS), clamped – clamped (CC), and clamped – simply supported (CS) were considered in this study.
The variations of buckling load, with the mode number for thin (a/h=20) symmetrically loaded laminated cross – ply (0/90/90/0) plate with modulus ratio (E1/E2=5) were computed and the results are given in Table 1 and Figure 6.
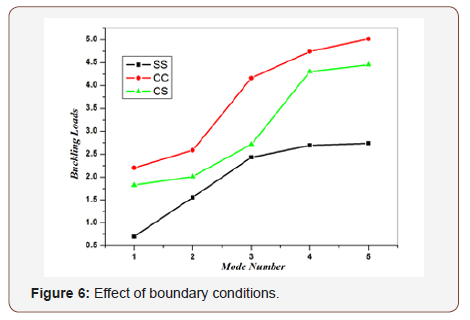
Table 1:The first five non – dimensional buckling loads 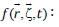 of symmetric (0/90/90/0) square laminated plates with a / h = 20 , and
E1 / E2 = 5 .
of symmetric (0/90/90/0) square laminated plates with a / h = 20 , and
E1 / E2 = 5 .

It is observed that, for all cases the buckling load increases with the mode number but at different rates depending on whether the plate is simply supported, clamped or clamped – simply supported. The buckling load is a minimum when the plate is simply supported and a maximum when the plate is clamped. Because of the rigidity of clamped boundary condition, the buckling load is higher than in simply supported boundary condition. It is also observed that as the mode number increases, the plate needs additional support.
Conclusion
of the rigidity of clamped boundary condition, the buckling load is higher than in simply supported boundary condition. It is also observed that as the mode number increases, the plate needs additional support.
Acknowledgement
None.
Conflict of Interests
No Conflict of Interest.
Author
Atbara, Sudan in 1966. He received his diploma degree in mechanical engineering from Mechanical Engineering College, Atbara, Sudan in 1990. He also received a bachelor’s degree in mechanical engineering from Sudan University of science and technology – Faculty of engineering in 1998, and a master’s degree in solid mechanics from Nile valley university (Atbara, Sudan) in 2003, and a PhD in structural engineering in 2017. He contributed in teaching some subjects in other universities such as Red Sea University (Port Sudan, Sudan), Kordofan University (Obayed, Sudan), Sudan University of Science and Technology (Khartoum, Sudan), Blue Nile University (Damazin, Sudan) and Kassala University (Kassala, Sudan). In addition, he supervised more than hundred and fifty under graduate studies in diploma and B.Sc. levels and about fifteen master theses. The author wrote about thirty-five engineering books written in Arabic language, and fifteen books written in English language and more than hundred research papers in fluid mechanics, thermodynamics, internal combustion engines and analysis of composite structures. He is currently an associated professor in Department of Mechanical Engineering, Faculty of Engineering and Technology, Nile Valley University Atbara, Sudan. His research interest and favorite subjects include structural mechanics, applied mechanics, control engineering and instrumentation, computer aided design, design of mechanical elements, fluid mechanics and dynamics, heat and mass transfer and hydraulic machinery. The author also works as a technical manager and superintendent of Al – Kamali mechanical and production workshops group which specializes in small, medium and large automotive overhaul maintenance and which situated in Atbara town in the north part of Sudan, River Nile State.

References
- Turvey GJ, Osman MY (1990) Elastic large deflection analysis of isotropic rectangular Mindlin plates. International Journal of mechanical sciences 32(4): 315-328.
- Turvey GJ, Osman MY (1989) Large deflection analysis of orthotropic Mindlin plates. proceedings of the 12th Energy resource technology conference and exhibition, Houston, Texas, pp. 163-172.
- Turvey GJ, Osman MY (1991) Large deflection effects in anti-symmetric cross-ply laminated strips and plates. I.H. Marshall, composite structures 6: 397-413.
- Osama Mohammed Elmardi (2014) Verification of dynamic relaxation (DR) method in isotropic, orthotropic and laminated plates using small deflection theory. International Journal of Advanced Science and Technology 72: 37-48.
- Osama Mohammed Elmardi Suleiman (2015) Nonlinear analysis of rectangular laminated plates using large deflection theory. International Journal of Emerging Technology and Research 2(5): 26-48.
- Osama Mohammed Elmardi Suleiman (2015) Validation of Dynamic Relaxation (DR) Method in Rectangular Laminates using Large Deflection Theory. International Journal of Advanced Research in Computer Science and Software Engineering 5(9): 137-144.
- Osama Mohammed Elmardi Suleiman(2015) Nonlinear analysis of rectangular laminated plates. Lap Lambert Academic Publishing, Germany and ISBN: (978-3-659-76787-6) .
- Osama Mohammed Elmardi Suleiman (2016) Text Book on Dynamic Relaxation Method. Lap Lambert Academic Publishing, Germany.
- Larry J Segelind (1984) Applied finite element analyses. Agricultural engineering department, Michigan state University, John Wiley and sons’ publishers.
- Amir Wadi Al Khafaji, John R Tooley (1986) Numerical methods in engineering practice. University of Evansville, CBS publishing Japan Ltd.
- Eastop TD, Mc Conkey A (1993) Applied thermodynamics for engineering technologists. fifth edition, John wiley and sons, New York.
- Osama Mohammed Elmardi Suleiman (2016) Introduction and Literature Review on Buckling of Composite Laminated Plates. Lap Lambert Academic Publishing, Germany.
- Osama Mohammed Elmardi Suleiman (2016) Bibliography and Literature Review on Buckling of Laminated Plates. International Journal of Science and Engineering 2(8): 104-112.
-
Osama Mohammed Elmardi Suleiman, Mahmoud Yassin Osman, Tagelsir Hassan. Effect of Boundary Conditions on Buckling Load for Laminated Composite Plates. Glob J Eng Sci. 2(1): 2019. GJES.MS.ID.000527.
-
Boundary conditions, Biaxial buckling, Classical laminated plate theory, Finite element, Fortran program, Composite laminated decks plates
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






