 Research Article
Research Article
Darcy Convection Anisotropic Problem with Multi Stability of Stationary Motions for Rectangle
Abdelhafez MA1,2* and Tsybulin VG1
1Southern Federal University, Russia
2Sohag University, Sohag, Egypt
Mostafa Abdallah Ahmed, Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt.
Received Date: May 23, 2019; Published Date: May 31, 2019
Abstract
Based on the Darcy model, fluid convection in a porous rectangle is analyzed taking into account anisotropy of thermal characteristics and permeability. Relations between parameters for which the problem belongs to the class of co-sssymmetric systems are derived. For this case explicit formulas for the critical numbers of the loss of stability of mechanical equilibrium are found. Using a finite-difference method that preserves the cosymmetry of the problem, family of stationary convective regimes is computed. Through the computational experiment the destruction of families is demonstrated in the case of violation of the conditions of co-symmetry. As result the appearance of a finite number of stationary regimes are obtained.
Keywords:Landslide; Erosion; Environmental disaster; Southeastern nigeria
Convection Equations of Heat-Conducting Fluid in A Porous Anisotropic Medium Based on Darcy’s Law
The plane problem of heating a rectangular container is considered Ω = [0, a] × [0, b], on the boundary of which the conditions of impermeability and temperature pro le linear in height are given T∗(y) = T2 − y(T2 − T1)/b, Where T1 И T2 temperature at the top (y = b) and bottom (y = 0) boundaries, respectively, the force of gravity acts in the direction opposite to the coordinate y. Next, a perturbation of the temperature field is introduced T (x, y, t) = T∗(y) + θ (x, y, t) and a transition is made to dimensionless quantities [1]. For stream function ψ and temperature deviations θ the following initial-boundary problem is obtained with respect to the linear profile:
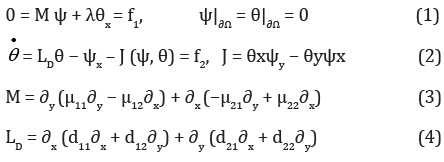
Here t - time, μij - the components of the tensor of dimensionless coefficients of reverse permeability, dij - coefficients thermal conductivity, λ - Rayleigh filtration number.
Equations (1)-(4) supplemented with initial conditions θ (x, y, 0) = θ0(0, y).
With μ11 = μ22 = d11 = d22 = 1 И μ12 = μ21 = d12 = d21 = 0 from (1)-(2) equations are obtained that correspond to the isotropic problem. In this case, the system of equations is co-symmetric according to [2], those there is a vector field L, which is orthogonal to the vector field of the problem and does not vanish on a nontrivial stationary solution. IN [1] set the conditions under which the task (1)-(4) is cosymmetric, these conditions are clarified by the following lemma.
Lemma
Under the conditions
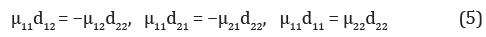
co-symmetry of the system (1)-(4) is a vector function L = (d22θ ,−μ11ψ
Mechanical Equilibrium Stability Analysis
Equations (1)-(4) satisfies zero solution θ = ψ = 0, corresponding to mechanical equilibrium. In the case of μ12 = μ21 = d12 = d21 = 0 from (1)-(4) for perturbations, a linear system is obtained
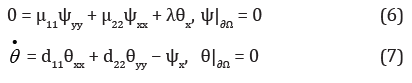
It turns out that critical Rayleigh numbers λ, corresponding to the monotonic instability of mechanical equilibrium, are given by the formula
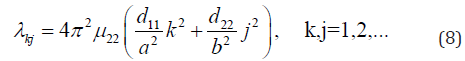
The emergence of the instability of mechanical equilibrium corresponds to the eigenvalue λ11. Critical values of the Rayleigh filtration number λ for isotropic case follow from (8) at μ22 = d 11 = d22 = 1. In [2] for the isotropic Darcy problem, it is shown that the first critical value λ11 twice for an arbitrary region, and when the transition parameter λ through λ11 from a state of mechanical equilibrium a family of stationary modes branches o (equilibria). The calculations performed in this paper showed that a similar scenario is realized for the Darcy anisotropic problem. The equilibrium family for the plane problem of filtration convection has a variable spectrum, this distinguishes the co-symmetric situation from the symmetric one. Every transition λ through subsequent critical values λkj corresponds to the bifurcation of the birth of a family of unstable stationary modes.
In case of violation of conditions (5) vector function L = (d22θ, -μ11ψ) is not a problem co-symmetry. In this case, instead of a oneparameter family, a finite number of convective regimes are formed. (stationary or non-stationary) [3-5].
Further numerical research is carried out for the case μij = dij = 0, (i ≠ j). Following [3], it turns out selective (selection) function
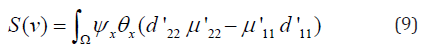
Here ψ and θ are the solution to the problem (1)-(4) on condition μ11d11 = μ22 d22 (case of co-symmetry) belonging to the family of stationary modes. Parameter ν sets parametrization on the family, ν ∈ [0, 1]. symbols 'ii μ И 'ij d denoted parameter values that differ from those for which the family is calculated. At μ'ii = μ'ii , d'ii = d'ii , (i = 1, 2) selective function S(ν) = 0. If a μ'ii ≠ μ'ii and/ or d'ii ≠ d'ii , (i = 1, 2), then there are modes corresponding to the solutions of the equation S(ν) = 0. If one parameter is disturbed d’11 = d11 + ε selective equation (9) will take the following form
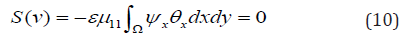
Numerical Study
In the case of anisotropy, the Darcy problem with co-symmetry in the [1] an analysis of the occurrence of stationary convective regimes, branching o from the loss of stability of mechanical equilibrium, is given. The conditions on the coefficients of the system under which the problem has co-symmetry and the branching of the continuous family of stationary modes are analytically determined. In this paper, the results of calculations of the families themselves are presented on the basis of the scheme [6], and the study of their destruction under violation of the conditions. Table 1 presents the results of calculations of the critical Rayleigh numbers depending on combinations of parameters of reverse permeability μii and thermal conductivity d22 ΠpИ d11 = 1, a = 2.5, b = 1. The value λ11, λ21 is calculated by the formula (8), and the quantities λh1 , λh2 , λh3 h meet the first three critical values on the grid 36 × 12. In the last column ⪡KOC⪢ notes the fulfillment of the conditions of co-symmetry (5).
Table 1:
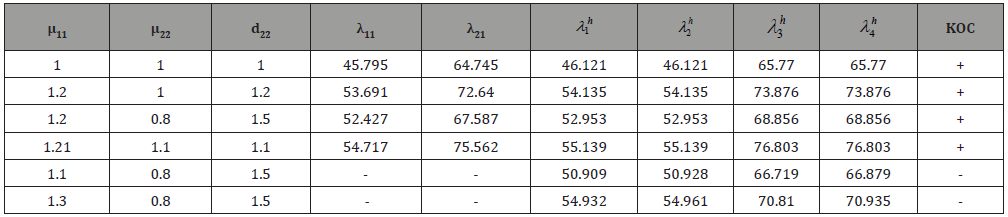
The first row of the table answers the isotropic problem [4], the next three lines are co-symmetries in the anisotropic case. The second line corresponds to the conditions given in [1], and the third and fourth conditions (5). Thus, the conditions for the existence of co-symmetry (5) allow you to expand the set of values of the coefficients for which you can apply the formula for calculating the critical Rayleigh numbers [1]. Critical numbers characterize the occurrence of convection as a result of monotonous loss of stability of mechanical equilibrium. The last two lines of the Table 1 present the results of calculating the critical numbers when the condition for the existence of co-symmetry is violated. It can be seen that the duplicity of the eigenvalues of the corresponding spectral problem disappears.
In Figure 1 calculated families of stationary modes are presented in coordinates Nuh
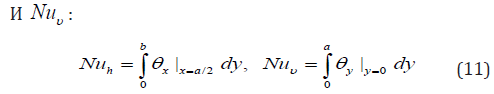
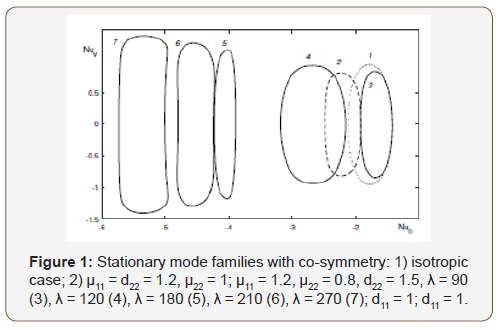
Isotropic case corresponds to the curve 1. With changing parameters μ11, d22, μ22, according to the formula (5), co-symmetry is preserved, while the family shifts, see curves 2 И 3. With the growth of the Rayleigh number λ the family increases in size and shifts towards negative values Nuh.
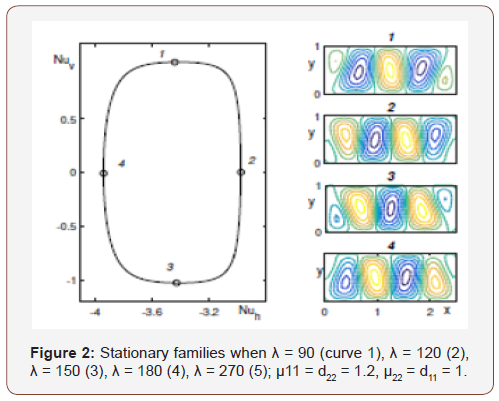
In Figure 2 on the left is a family curve calculated at λ = 150. The dots mark the stationary modes, the stream functions of which are given on the right. Depending on the position of the point on the family, the resulting mode consists of four shafts (points 2, 4) or three main and two angular shafts (points 1,3).
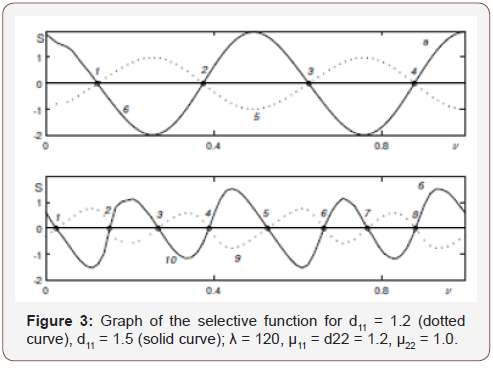
In Figure 3 graphs of discrete analogue of the selective function are presented (10) for μ11 = d22 = 1.2, μ22 = 1.0 and various meanings d11. When the perturbation of the parameter d11 = d11 + ε grid analog of the selective equation (10) has the following form:
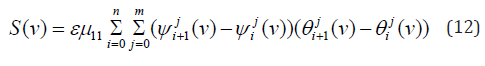
Here through j ( ) ψij(v),θij(v) marked temperature and current function corresponding to the point family of stationary modes with number ν.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Abdelhafez MA, Tsybulin VG (2017) Anisotropy effect on the convection of a heat-conducting fluid in a porous medium and cosymmetry of the darcy problem. Fluid Dynamics 52(1): 49-57.
- Yudovich VI (1991) Cosymmetry, degeneration of solutions of operator equations, and onset of a filtration convection. Mathematical Notes of the Academy of Sciences of the USSR 49(5): 540-545.
- Yudovich VI (2004) Bifurcations for Perturbations Violating Cosymmetry. Dokl Ross Akad Nauk 398: 57-61.
- Tsybulin V, Karas ozen B (2008) Destruction of the family of steady states in the planar problem of Darcy convection. Phys Lett A 372(35): 5639-5643.
- Govorukhin VN, Shevchenko IV (2017) Multiple equilibria, bifurcations and selection scenarios in cosymmetric problem of thermal convection in porous medium. Phys D 361: 42-58.
- Abdelhafez MA, Tsybulin VG (2017) Nuumerical simulation of convective motion in an anisotropic porous medium and cosymmetry conservation. Computational Mathematics and Mathematical Physics 57(10): 1706- 1719.
-
Boniface CE Egboka, Akudo Ernest Orji, Hycienth O Nwankwoala. Gully Erosion and Landslides in Southeastern Nigeria: Causes, Consequences and Control Measures. Glob J Eng Sci. 2(4): 2019. GJES.MS.ID.000542.
-
Heat-Conducting Fluid, Darcy Convection, Anisotropic Problem, Stationary Motions, Rectangle
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






