Cross-correlation based Underwater Node Estimation Technique and a Concise Summary of Different Effects on It

Use of protocol-based techniques for node estimation in in underwater wireless communication network (UWCN) is very difficult because of the propagation characteristics of underwater environment. Hence, in this thesis, a statistical tool-based estimation process is implemented, and this tool is called crosscorrelation. However, a matter is greatly important that the nodes can the distributed according to different types of distributions. Six different types of distributions called exponential distribution, normal distribution, Rayleigh distribution, gamma distribution, Weibull distribution and chi-squire distribution, are considered with respect to two sensors, as the distribution of numerous nodes. The estimation of nodes at each of these distribution cases is the key work in this thesis. Though the thesis is performed for underwater environment, it can be equally implemented to other network environments such as space communication networks (SCNs), terrestrial communication networks (TCNs), and underground communication networks (UGCNs). In ad hoc type of networks, number of active nodes can vary with time and that’s why counting the number of active nodes is very useful for proper operation and maintenance of the networks. The key importance of node estimation of different types of network is given bellow [1].

• Maintaining coverage area in wireless sensor network (WSN)

• Providing proper identification of tagged body in RFID system. To count speakers in multi-speaker teleconferencing system

• To regain network topology

• Assisting traffic management in mobile ad hoc network

• Background noise calculation

In the recent advancement of underwater communication, the underwater wireless sensor networks become one of the most effective areas due to its importance. Both acoustic waves [2,3] and magnetic waves [4,5] are used here. However, Underwater acoustic sensor networks (UASN) are more flexible form of communication in underwater environment, which have several applications, such as monitoring daily ocean life, seismic and volcanic prediction, oceanographic data collection, pollution monitoring, deep-sea archaeology, seawater data collection [6], offshore exploration, climatic data collection, disaster alleviation [7], environmental research, oil/gas spills keeping track of, tactical surveillance.

In UWCNs, the signal propagation is completely different than the signal propagation in TCNs because of changing of medium. Relative to TCNs, more challenges are faced at UWCNs for signal propagation due to its water-medium. There are three possible physical waves used in UWCNs as underwater communication carriers, electromagnetic (EM) wave, optical wave and acoustic wave. Because of being high frequency of EM wave, it suffers from very high absorption in underwater environment, therefore, can only propagate extremely short distances [8]. Optical waves have a rapid attenuation in water due to absorption and backscattering [9]. Underwater acoustic communication poses the limitation of long and variable delays, high path losses, strong background noises and multipath of signal propagation [10]. Despite of these limitations acoustic waves are commonly used in UWCNs, as they can propagate over long distances [11]. In this thesis, the proposed node estimation technique is performed in underwater wireless acoustic sensor networks (UWASNs).

Node estimation of underwater network is difficult using terrestrial node estimation methods because there are some characteristics of underwater environment such as large propagation latency, node mobility, non-negligible capture effect, and high error rate which creates problem in estimation. For this reason, node estimation method based on cross- correlation of Gaussian signals is used for underwater network. In this process different estimation parameters can be formulated from the crosscorrelation function (CCF). However, cross-correlation is a novel signal processing tool which is used in fish estimation to node estimation [12-18]. Cross-correlation based node estimation using mean and standard deviation is the main goal of this paper. We have used three sensors straight line case in this paper.

There have been many investigations regarding the use of the ambient noise cross-correlation to extract the time-domain GF in various environments and frequency ranges of interest, for example, underwater acoustics. The procedural steps for determining the noise CCF are similar for all the above-mentioned environments. In brief, the procedure is as follows: firstly, the signals from a number of different noise sources are collected by two sensors separated by a certain distance in the region of interest; secondly, the received signals are summed at each of the two sensor locations; and, finally, these two noise signals are cross-correlated.

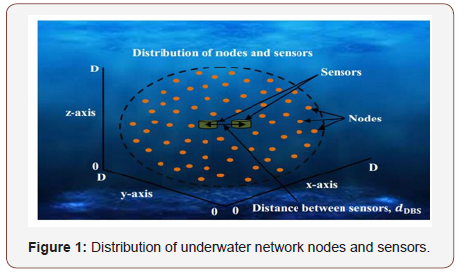
Gaussian signal has a certain property that, cross-correlation of two Gaussian signals results a delta function, which is the basic idea of this estimation method and also the reason of using Gaussian signals as transmitted signals. The propagation velocity is assumed to be constant, which is the sound velocity ‘Sp’ in the medium (Figure 1).

Most researchers have only tried to retrieve an estimate of the GF; for example, it has been shown theoretically that the GF can be obtained with ambient noise cross-correlation in the simple case of a homogeneous medium with attenuation.

Two sensors in line

To estimate the number of nodes we use CCF formulation. For this formulation, a 3D spherical region is considered as network, which contains N evenly distributed nodes. Two sensors send probe request and every node in the network transmit Gaussian signals at the same time in respond to that probe request using acoustic wave as the underwater communication carrier. Simultaneously transmitted Gaussian signals form N nodes summed at each sensor location with different delay differences to form composite Gaussian signals and these composite signals are then received by the sensors.

Bins, b in the CCF (Figure 2) is defined as a place occupied by a delta inside a space of a width twice the distance between sensors and that place is determined by the delay difference of the signal coming to the sensors [13,16-20]. The deltas of equal delay differences are placed in that particular bin.

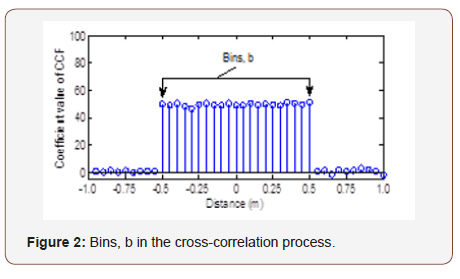
Different cardinality estimation parameters can be obtained from this CCF. Network cardinality can be estimated using these parameters.

Three sensors in line (SL)

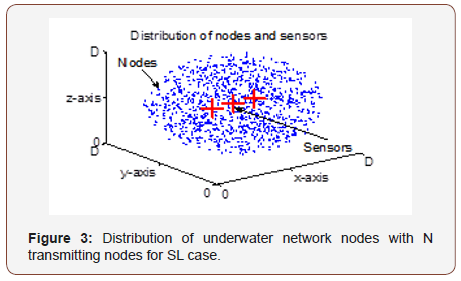
For three sensors let us consider a 3D network containing N nodes, where the nodes are evenly distributed over the dimensions of a large sphere. In SL case, three sensors are located in a line inside the network, where the middle sensor lies on the center of the 26 spheres. The other two probing nodes are placed on both sides of and at equal distances from the middle one along a line as shown in Figure 3. Simultaneous transmission of Gaussian signals from N nodes is initiated after receiving probe request from the probing nodes (sensors). These Gaussian signals form composite Gaussian signals at three sensor locations. CCFs are formulated from the cross-correlation of these three composite signals.

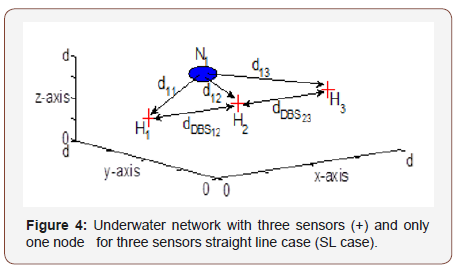
The 3D space is considered as a cube such that the dimension of the cube is equal to the diameter of the sphere and three sensors, H1, H2 and H3, and a node N1, are placed at locations (x₁,y₁,z₁), (x₂,y₂,z₂), (x₃,y₃,z₃) respectively, inside the sphere as shown in the Figure 4. The distance between sensors, then

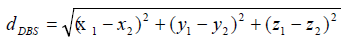
Mean of CCF, μ

Mean of CCF increases with the increase of signal strength and decreases with the decrease of signal strength. It is expressed as

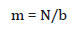
where, bin, b can be expresses as [1,13,19,20]. NSBS means number of samples between sensors. Standard deviation of CCF can be expressed as,

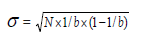
Standard Deviation is also affected by signal strength.

The ratio of standard deviation to the mean is:

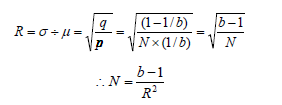
This is not affected by signal length as it is the ratio of two independent parameter.

Review stage

Submit your manuscript electronically for review.

Final stage

When you submit your final version, after your paper has been accepted, prepare it in two-column format, including figures and tables.

Figures

As said, to insert images in Word, position the cursor at the insertion point and either use Insert | Picture | From File or copy the image to the Windows clipboard and then Edit | Paste Special | Picture (with “Float over text” unchecked).

The authors of the accepted manuscripts will be given a copyright form and the form should accompany your final submission.

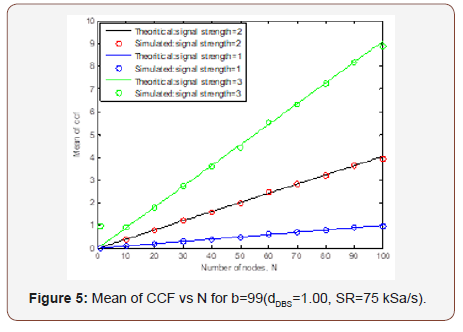
Simulations are performed using MATLAB as the programming tool. We take three values of signal strength 1,2, 3 for b=99 (d_DBS=1.00, SR=75 kSa/s) to get the results for Mean of CCF vs. N which is shown in Figure 5.

Similarly, we take three values of signal strength 1, 2, 3 for b=49(d_DBS=0.5, SR=75 kSa/s) to get the results for mean of CCF vs. N which is shown in Figure 6.

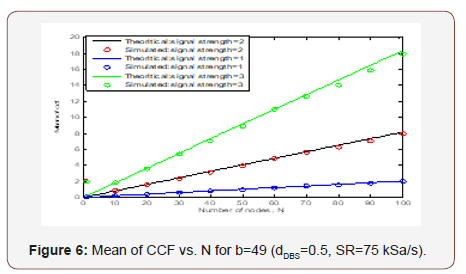
From above figures it is shown that the mean of CCF is closely attached with the theoretical line. This means our estimation is accurate. To estimate with Standard deviation, we take three values of signal strength 1, 2, 3 for b=149 (d_DBS=1.5, SR=75 kSa/s) to get the results for Standard Deviation of CCF vs. N which is shown in Figure 7.

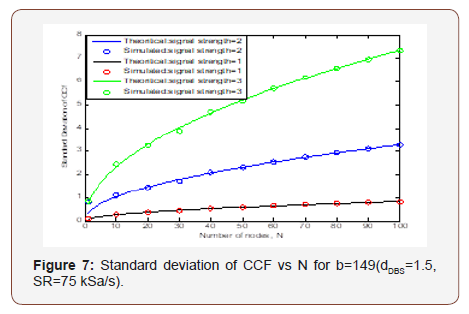
The simulation result for Standard deviation of CCF vs N with three values of signal strength 1,2, 3 for b=199 (d_DBS=2.00, SR=75 kSa/s) is shown in Figure 8.

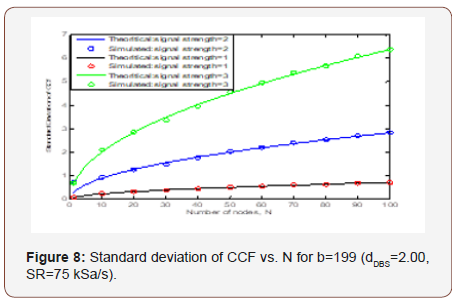
From the above figure we can say that by using standard deviation as estimation parameter we can properly estimate nodes. We see that the theoretical results and simulated results match appropriately.

Different effects on cross-correlation based node estimation technique are discussed in this section.

Effect on signal strength

The estimation parameters derived from the CCF are affected from signal strength Ss. Cross correlation of two Gaussian signals with unity signal strength results a delta function of strength one. It is the basic idea of this estimation approach and also the reason of using Gaussian signals as transmitted signals. If Gaussian signals are correlated with signal strength 2 then a delta of strength four is obtained. Similarly, for the half signal strength of the Gaussian signals, the strength of the delta is one-quarter. So, strength of the deltas in the bins of the CCF is affected by Ss and the strength of the deltas is proportional to the square of Ss. The strength of deltas in the bins of CCF is affected by signal strength and the strength of deltas are proportional to signal strength. signal strength dependency of the strength of deltas in the bins of the CCF, coefficient values of CCF vary with Ss, which means sum, mean and standard deviation of those coefficient values also vary with Ss. With this finding we can say that, three estimation parameters: sum, mean and standard deviation of CCF are affected by Ss.

So, the estimation parameters which are derived from CCF mean, sum and standard deviation are also proportional to the square of Ss. The modified versions of sum, mean and standard deviation are expressed as

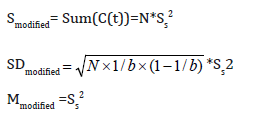
No modifications are required for these two parameters, which suggest that, R_msd and R_sdm of CCF are independent of Ss and the expressions of these two estimation parameters.

Use of non-gaussian signals

Non-Gaussian signals can be used as the transmitting signals to provide a useful alternative of the Gaussian signals. If Non-Gaussian signals are used, the CCFs will contain some undesired peaks. These undesired peaks can be removed using proper manipulation of the CCFs. The cross-correlation of Non-Gaussian signals can be used for node estimation.

Dopler effect

In underwater acoustic networks the Doppler Effect is one of the important practical issues. The frequency of the received signal sometimes compresses and sometimes spreads according to the movement of the source and receiver moving towards or away from each other. Spreading of a signal requires more time to reach the sensors. So, it requires more time and energy for estimation. To investigate the estimation performance with Doppler Effect, the frequency of the received signal has to be adjusted.

Effect of bandwidth

Limited bandwidth gives sinc function instead of delta function of infinite band signal. Channel bandwidth restricts the signal bandwidth which might affect the estimation performance. It is proved that the scaling is good enough to get estimation in finite BW case as in infinite BW case. As the R_finiteBW is a constant multiple of R_infiniteB, the power which affects the CV of R_finiteBW in estimation expression is not changed. So, the CV is not affected by the BW (10 kHz). So, from these we can say that no problem will occur with the BW greater than 10 kHz but whether it is affected or not with the BW less than 10 kHz should have to be checked.

Estimation of nonuniformity

Different distribution of nodes will change the shape of the CCFs, and it will affect the estimation performance. It is required to investigate the performance of the proposed methods with various types of distributed nodes. To estimate the number of nodes with different node distribution modified estimation parameters are needed.

Unequal sensor distance (USD)

Unequal distances between the sensors without affecting the estimation performance are possible. We used equal distances between the sensors in the proposed techniques, which might be difficult in some practical cases. For both SL and TS cases it is possible to estimate the number of nodes with unequal distances between the sensors.

In this paper, we have measured the performance of standard deviation and mean of CCF as estimation parameter using crosscorrelation based node estimation technique. We have used three sensors SL case here. In future, we will investigate three sensors case for TS case of node estimation similarly. We will also take different number of bins and different signal strengths to compare the results. Our findings will assist the future researchers.

None.

No Conflict of Interest.

1. ANOWER MS (2011) Estimation using cross-correlation in a communications network (Doctoral dissertation, Australian Defence Force Academy). Pp. 1-308.
2. Chitre M, Shahabudeen S, Freitag L, Stojanovic M (2008) Recent advances in underwater acoustic communications & networking. In OCEANS, IEEE, pp. 1-10.
3. Jiang Z (2008) Underwater acoustic networks–issues and solutions. International journal of intelligent control and systems 13(3): 152-161.
4. Abdou AA, Shaw A, Mason A, Al Shammaa, A, Cullen J, et al. (2011) Electromagnetic (EM) wave propagation for the development of an Underwater Wireless Sensor Network (WSN). In Sensors, IEEE, pp. 1571-1574.
5. Elrashidi A, Elleithy A, Albogame M, Elleithy K (2012) Underwater wireless sensor network communication using electromagnetic waves at resonance frequency 2.4 GHz. In Proceedings of the 15th Communications and Networking Simulation Symposium. Society for Computer Simulation International, pp. 1-13.
6. Baronti F, Fantechi G, Roncella R, Saletti R (2012) Wireless sensor node for surface seawater density measurements. Sensors (Basel) 12(3): 2954-2968.
7. Soreide NN, Woody CE, Holt SM (2001) Overview of ocean based buoys and drifters: Present applications and future needs. In OCEANS, 2001. MTS/IEEE Conference and Exhibition 4: 2470-2472.
8. Che X, Wells I, Dickers G, Kear P, Gong X (2010) Re-evaluation of RF electromagnetic communication in underwater sensor networks. Communications Magazine, IEEE 48(12): 143-151.
9. Liu L, Zhou S, Cui JH (2008) Prospects and problems of wireless communication for underwater sensor networks. Wireless Communications and Mobile Computing 8(8): 977-994.
10. Akyildiz IF, Pompili D, Melodia T (2004) Challenges for efficient communication in underwater acoustic sensor networks. ACM Sigbed Review 1(2): 3-8.
11. Sozer EM, Stojanovic M, Proakis JG (2000) Underwater acoustic networks. Oceanic Engineering, IEEE Journal of 25(1): 72-83.
12. Schaff DP, Waldhauser F (2005) Waveform cross-correlation-based differential travel-time measurements at the Northern California Seismic Network. Bulletin of the Seismological Society of America 95(6): 2446-2461.
13. Hossain SA, Mallik A, Arefin M (2017) A Signal Processing Approach to Estimate Underwater Network Cardinalities with Lower Complexity. Journal of Electrical and Computer Engineering Innovations 5(2): 131- 138.
14. Anower MS, Frater MR, Ryan MJ (2009) Estimation by cross-correlation of the number of nodes in underwater networks. In Telecommunication Networks and Applications Conference (ATNAC), Australasian, pp. 1-6.
15. Hossain SA, Hossen M, Anower S (2018) Estimation of damselfish biomass using an acoustic signal processing technique. Journal of Ocean Technology 13(2).
16. Rana MS, Anower MS, Siraj SN, Haque MI (2014) A signal processing approach of fish abundance estimation in the sea. In Strategic Technology (IFOST), 9th International Forum on pp. 87-90.
17. Hossain SA, Hossen M (2018) Abundance estimation from different distribution of damselfish using cross-correlation and three sensors. New Zealand Acoustics 31(3).
18. Hossain SA, Hossen M (2018) Biomass Estimation of a Popular Aquarium Fish Using an Acoustic Signal Processing Technique with Three Acoustic Sensors. In Advancement in Electrical & Electronic Engineering (ICAEE), 2015, International Conference on. IEEE.
19. Hossain SA, Anower MS, Halder A (2015) A cross-correlation based signal processing approach to determine number and distance of objects in the sea using CHIRP signal. In Electrical & Electronic Engineering (ICEEE), International Conference on pp. 177-180.
20. Hossain SA, Ali MF, Akif MI, Islam R, Paul AK, et al. (2016) A determination process of the number and distance of sea objects using CHIRP signal in a three sensors based underwater network. In Electrical Engineering and Information Communication Technology (ICEEICT), 3rd International Conference on pp. 1-6.