Artificial Neural Networks and Hopfield Type Modeling

From the mathematical point of view, an artificial neural network corresponds to a non- linear transformation of some inputs into certain outputs. Many types of neural networks have been proposed and studied in the literature and the Hopfield-type network has be- come an important one due to its potential for applications in various fields of daily life.

A neural network is a network that performs computational tasks such as associative memory, pattern recognition, optimization, model identification, signal processing, etc. on a given pattern via interaction between a number of interconnected units characterized by simple functions. From the mathematical point of view, an artificial neural network corresponds to a nonlinear transformation of some inputs into certain outputs. There are a number of terminologies commonly used for describing neural networks. Neural networks can be characterized by an architecture or topology, node characteristics, and a learning mechanism [1]. The interconnection topology consists of a set of processing elements arranged in a particular fashion. The processing elements are connected by links and have weights associated with them. Each processing elements is associated with:

• A state of activation (state variable)

• An output function (transfer function)

• A propagation rule for transfer of activation between processing elements

• An activation rule, which determines the new state of activation of a processing element from its inputs weight associated with the inputs, and current activation.

Neural networks may also be classified based on the type of input, which is either binary or continuous valued, or whether the networks are trained with or without supervision. There are many different types of network structures, but the main types are feed-forward networks and recurrent networks. Feed-forward networks have unidirectional links, usually from input layers to output layers, and there are no cycles or feedback connections. In recurrent networks, links can form arbitrary topologies and there may be arbitrary feed- back connections. Recurrent neural networks have been very successful in time series prediction. Hopfield networks are a special case of recurrent networks. These networks have feedback connections, have no hidden layers, and the weight matrix is symmetric.

Neural networks are analytic techniques capable of predicting new observations from other observations after executing a process of so-called learning from existing data. Neural network techniques can also be used as a component of analysis designed to build explanatory models. Now there is neural network software that uses sophisticated algorithms directly contributing to the model building process.

In 1943, neuro physiologist Warren McCulloch and mathematician Walter Pitts [2] wrote a paper on how neurons might work. In order to describe how neurons in the brain might work, they modeled a simple neural network using electrical circuits. As computers be- came more advanced in the 1950’s, it was possible to simulate a hypothetical neural net- work. In 1982, John Hopfield presented a paper [3]. His approach was to create more useful machines by using bidirectional lines. The model proposed by Hopfield, also known as Hopfield’s graded response neural network, is based on an analogue circuit consisting of capacitors, resistors and amplifiers. Previously, the connections between neurons was only one way. At the same years, scientist introduced a “Hybrid network” with multiple layers, each layer using a different problem-solving strategy.

Now, neural networks are used in several applications. The fundamental idea behind the nature of neural networks is that if it works in nature, it must be able to work in computers. The future of neural networks, though, lies in the development of hardware. Research that concentrates on developing neural networks is relatively slow. Due to the limitations of processors, neural networks take weeks to learn. Nowadays trying to create what is called a “silicon compiler”, “organic compiler” to generate a specific type of integrated circuit that is optimized for the application of neural networks. Digital, analog, and optical chips are the different types of chips being developed.

The brain manages to perform extremely complex tasks. The brain is principally com- posed of about 10 billion neurons, each connected to about 10,000 other neurons. Each neuronal cell bodies (soma) are connect with the input and output channels (dendrites and axons). Each neuron receives electrochemical inputs from other neurons at the dendrites. If the sum of these electrical inputs is sufficiently powerful to activate the neuron, it transmits an electrochemical signal along the axon, and passes this signal to the other neurons whose dendrites are attached at any of the axon terminals. These attached neurons may then fire. It is important to note that a neuron fires only if the total signal received at the cell body exceeds a certain level. The neuron either fires or it doesn’t, there aren’t different grades of firing. So, our entire brain is composed of these interconnected electro- chemical transmitting neurons. This is the model on which artificial neural networks are based. Thus for, artificial neural networks haven’t even come close to modeling the complexity of the brain, but they have shown to be good at problems which are easy for a human but difficult for a traditional computer, such as image recognition and predictions based on past knowledge.

Fundamental difference between traditional computers and artificial neural networks is the way in which they function. One of the major advantages of the neural network is its ability to do many things at once. With traditional computers, processing is sequential– one task, then the next, then the next, and so on. While computers function logically with a set of rules and calculations, artificial neural networks can function via Equation, pictures, and concepts. Based upon the way they function, traditional computers have to learn by rules, while artificial neural networks learn by example, by doing something and then learning from it.

Hopfield neural networks have found applications in a broad range of disciplines [3-5] and have been studied both in the continuous and discrete time cases by many researchers. Most neural networks can be classified as either continuous or discrete. In spite of this broad classification, there are many real-world systems and natural processes that behave in a piecewise continuous style interlaced with instantaneous and abrupt changes (impulses). Periodic dynamics of the Hopfield neural networks is one of the realistic and attractive modellings for the researchers. Hopfield networks are a special case of recurrent networks. These networks have feedback connections, have no hidden layers, and the weight matrix is symmetric. These networks are most appropriate when the input can be represented in exact binary form. Signal transmission between the neurons causes time delays. Therefore, the dynamics of Hopfield neural networks with discrete or distributed delays has a fundamental concern. Many neural networks today use less than 100 neurons and only need occasional training. In these situations, software simulation is usually found sufficient. Expected and optimistic development on all current neural network’s technologies will improve in very near future and researchers develop better methods and network architectures.

In the present paper, we briefly summarized historical background as well as developments of the artificial neural networks and present recent formulations of the continuous and discrete counterpart of a class of Hopfield-type neural networks modeling using functional differential equations in the presence of delay, periodicity, impulses and finite distributed delays. Combining some ideas of [4,6-10] and [11], we obtain a sufficient condition for the existence and global exponential stability of a unique periodic solution of the discrete system considered.

An artificial neural network (ANN) is an information processing paradigm that is in- spired by the way biological nervous systems, such as the brain, process information sees more details [12] and references given therein. The key element of this paradigm is the novel structure of the information processing system. It is composed of a large number of highly interconnected processing elements (neurons) working in unison to solve specific problems. ANNs, like people, learn by example. An ANN is configured for a specific application, such as pattern recognition or data classification, through a learning process. Learning in biological systems involves adjustments to the synaptic connections that exist between the neurons. This is true of ANNs as well.

The first artificial neuron was produced in 1943 by the neurophysiologist Warren McCulloch and the logician Walter Pitts [2]. But the technology available at that time did not allow them to do too much. Neural networks process information in a similar way the human brain does. The network is composed of a large number of highly interconnected processing elements (neurons) working in parallel to solve a specific problem. Neural net- works learn by example. Much is still unknown about how the brain trains itself to process information, so theories abound.

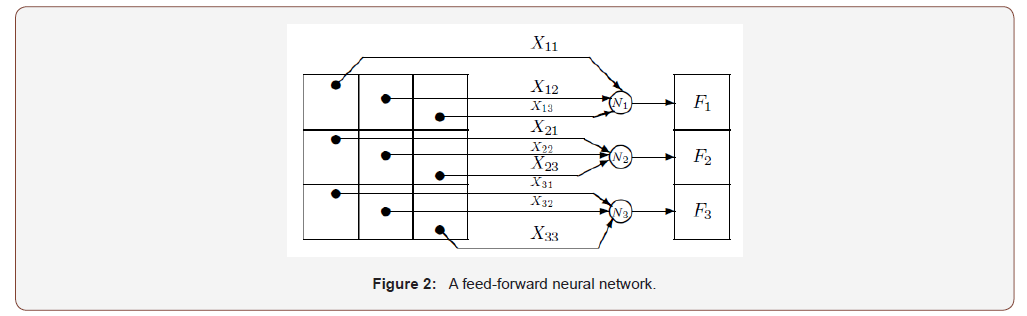
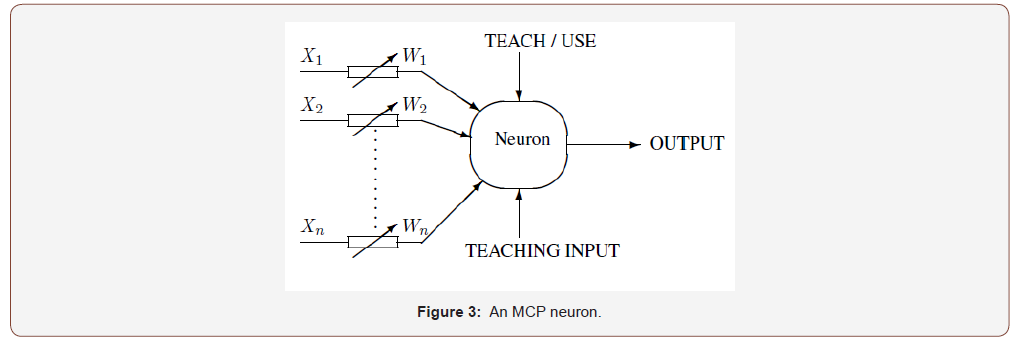
An artificial neuron is a device with many inputs and one output (Figure 1). The neuron has two modes of operation; the training mode and the using mode. In the training mode, the neuron can be trained to fire (or not), for particular input patterns. In the using mode, when a taught input pattern is detected at the input, its associated output becomes the current output. If the input pattern does not belong in the taught list of input patterns, the firing rule is used to determine whether to fire or not. An important application of neural networks is pattern recognition. Pattern recognition can be implemented by using a feed-forward (Figure 2) neural network that has been trained accordingly. During training, the network is trained to associate outputs with in- put patterns. When the network is used, it identifies the input pattern and tries to output the associated output pattern. The power of neural networks comes to life when a pattern that has no output associated with it, is given as an input. In this case, the network gives the output that corresponds to a taught input pattern that is least different from the given pat- tern. Hopfield-type neural networks are mainly applied either as associative memories or as optimization solvers. In both applications, the stability of the networks is prerequisite. The equilibrium points (stable states) of networks characterize all possible optimal solutions of the optimization problem, and stability of the network’s grantee the convergence to the optimal solutions. Therefore, the stability is fundamental for the network design. As a result of this fact the stability analysis of the Hopfield-type networks has received extensive attention from the many researchers, [4,6-9,11,13] and references given therein. The above neuron does not do anything that conventional computers do not already do. A more sophisticated neuron (Figure 3) is the McCulloch and Pitts model (MCP). The difference from the previous model is that the inputs are ‘weighted’, the effect that each input has at decision making is dependent on the weight of the particular input. The weight of an input is a number which when multiplied with the input gives the weighted input. These weighted inputs are then added together and if they exceed a pre-set threshold value, the neuron fires. In any other case the neuron does not fire. In mathematical terms, the neuron fires if and only if

X₁W1 + X₂₂ + X₃W₃ + …. > T,

where W_i, i = 1, 2, . . ., are weights, Xi, i = 1, 2, . . ., inputs, and T a threshold. The addition of input weights and of the threshold makes this neuron a very flexible and powerful one. The MCP neuron has the ability to adapt to a particular situation by changing its weights and/or threshold. Various algorithms exist that cause the neuron to ‘adapt’; the most used ones are the Delta rule and the back-error propagation. The former is used in feed-forward networks and the latter in feedback networks.

Neural networks have wide applicability to real world business problems. In fact, they have already been successfully applied in many industries. Since neural networks are best at identifying patterns or trends in data, they are well suited for prediction or forecasting needs including sales forecasting, industrial process control, customer research, data validation, risk management, target marketing.

ANN are also used in the following specific paradigms: recognition of speakers in communications; diagnosis of hepatitis; recovery of telecommunications from faulty software; interpretation of multi-meaning Chinese words; undersea mine detection; texture analysis; three-dimensional object recognition; hand-written word recognition; and facial recognition.

Hopfield-type (additive) networks have been studied intensively during the last two decades and have been applied to optimization problems [3-10,14-18]. Their starting point was marked by the publication of two papers [9, 10] by Hopfield. The original model used two-state threshold ‘neurons’ that followed a stochastic algorithm: each model neuron i had two states, characterized by the values (which may often be taken as 0 and 1, or 1 and 1, respectively). The input of each neuron came from two sources, external inputs I_i and inputs from other neurons. The total input to neuron i is then

where T_ij can be biologically viewed as a description of the synaptic interconnection strength from neuron j to neuron i. The motion of the state of a system of N neurons in state space describes the computation that the set of neurons is performing. A model therefore must describe how the state evolves in time, and the original model describes this in terms of a stochastic evolution. Each neuron samples its input at random times. It changes the value of its output or leaves it fixed according to a threshold rule with thresholds Ui [3,5]:

The simplest continuous Hopfield network is described by the differential equation

where x(t) is the state vector of the network, W represents the parametric weights, and f is a nonlinearity acting on the states x(t), usually called activation or transfer function.

In order to solve problems in the fields of optimization, neural control and signal processing, neural networks have to be designed such that there is only one equilibrium point and this equilibrium point is globally asymptotically stable so as to avoid the risk of having spurious equilibria and local minima. In the case of global stability, there is no need to be specific about the initial conditions for the neural circuits since all trajectories starting from anywhere settle down at the same unique equilibrium. If the equilibrium is exponentially asymptotically stable, the convergence is fast for real- time computations. The unique equilibrium depends on the external stimulus. The nonlinear neural activation functions are usually chosen to be continuous and differentiable nonlinear sigmoid functions satisfying the following conditions:

Some examples of activation functions are

where sgn (•) is a signum function and all the above nonlinear functions are bounded, monotonic and nondecreasing functions. It has been shown that the absolute capacity of an associative memory network can be improved by replacing the usual sigmoid activation functions. There, it seems appropriate that nonmonotonic functions might be better candidates for neuron activation in designing and implementing an artificial neural net- work.

One of the most widely used techniques in the study of models involving ordinary differential equations is to approximate the system by means of a system of difference equations, whose solutions are expected to be samples of the solutions of differential equations at discrete instants of time as in the case of Euler-type methods and Runge-Kutta methods. It has been shown by several authors [4,8] that the dynamics of numerical discretization’s of differential equations can differ significantly from those of the original differential equations. Consider for example the simple scalar differential equations [9].

A Euler-type discretization of equation (2) leads to a discrete version of the form

where denotes the discretization step size and y(n) denotes the value of y(t) for t = nh. Solutions of (2) and (3) are, respectively, given by

where y(t) → 0 as t → ∞ and the convergence is monotonic. However, y(n) of (3) for various values of h > 0 has the following Behaviours:

• 0 < h < 1: y(n) → 0 as n → ∞ — monotonic convergence.

• h = 1: y(n) = 0 for all n = 1, 2, 3, . . . and any choice of y (0).

• 1 < h < 2: y(n) oscillatory with y(n) →0 n→ ∞— oscillatory convergence.

• h = 2: y(n) is periodic with period p = 2.

• h > 2: y(n) is oscillatory and y(n) →∞ as n → ∞.

This example demonstrates the possibility that the standard Euler method produces spurious dynamics which certainly are not present in the original continuous-time version. See more detail [4,8,9] and references therein.

The global stability characteristics of the systems supplemented with impulses conditions in the continuous-time case one of the interesting and simple modeling. The presence of impulses requires some modifications and the imposing of additional conditions on the systems. Dynamical systems are often classified into two categories:

Continuous-time or discrete-time systems. In recent studies [4,6-10,19] there has been introduced a new category of dynamical systems, which is neither purely continuous- time nor purely discrete- time ones; these are called dynamical systems with impulses. Impulsive category of dynamical systems are combination of characteristics of both the continuous-time and discrete-time systems.

Sufficient conditions for global stability and exponential stability of equilibria of continuous-time Hopfield-type network with impulses studied by number of researchers [4,6-10] and references therein. Following Hopfield-type model of neural net- work with impulses [6-7] studied in the various form of formulations such as inserting time delays and modifying the system to a system of integra- differential equations.

where are the impulses at moments t_k and t₁ < t₂ < . . . is a strictly increasing sequence such that corresponds to the membrane potential of the unit i at time denotes a measure of response or activation to its incoming potentials; bij denotes the synaptic connection weight of the unit j on the unit i; the constants ci correspond to the external bias or input from outside the network to the unit i; the coefficient ai is the rate with which the unit self-regulates or resets its potential when isolated from other units and inputs.

As usual in the theory of impulsive differential equations, at the points of discontinuity t_k of the solution we assume It is clear that, in general, the derivatives do not exist. On the other hand, according to the first equality of (4) there exist the limitsAccording to the above convention, we assume that

The generalization of the system (4) such as introducing time delays, impulses and so on has been studied by many researchers [1,2]. For example;

This system is supplemented with initial functions of the form

where is continuous for s ∈ [−τ, 0].

At the beginning mostly assumed that the time delays are discrete. While this assumption is not unreasonable, a more satisfactory hypothesis is that the time delays are continuously distributed over a certain duration of time. Subject to the introduced conditions, modification of the system (4) to a system of integra-differential equations is investigated with the following systems [6]:

For an integra-differential equation an impulsive condition including both the functional value and its integral also seems natural. We take the impulse conditions in the form

where are measurable functions, essentially bounded on the respective interval, B_ik and α_ik are some real constants. For more details about impulse conditions of this and more general form see [4,6,8-10,13,20] and reference therein.

The recent work [17] deals with a family of sufficient conditions that govern the net- work parameters and the activation functions is established for the existence of a unique equilibrium state of the network. It has been shown by number of researchers [9,21] and references therein that; the capacity of an associative memory network can be significantly improved if the sigmoidal functions are replaced by non-monotonic activation functions. This is the one of the main major advances in the area of artificial neural networks.

Rearranging the network described by (15)

in which the sequence of times

where the value θ > 0 denotes the minimum time of interval between successive impulses. A sufficiently large value of θ ensures that impulses do not occur too frequently, but θ → ∞ means that the network becomes impulse free.

The vector solution x(t) = has components xi(t) piecewise continuous on (0, β) for some β > 0, such that the limits for i ∈ I, k ∈ N exist and x(t) is differentiable on the open intervals The functions I_k : R → R that characterize the impulsive jumps are continuous; the initial function φi : ( , 0] R is piecewise continuous and bounded in the sense of either

and the self-regulating parameter ai has a positive value, the synaptic connection weights bij are real constants, and the external biases ci denote real numbers. The delay kernels K_ij : [0, ∞) → R are piecewise continuous and satisfy

in which κ (•) corresponds to some nonnegative function defined on [0, ∞) and the constant μ0 denotes some positive number ; and also, the activation function fj : R→R is globally Lipschitz continuous with a Lipschitz constant Lj > 0 – namely

An equilibrium state of the impulsive network denoted by the constant vector where the components are governed by the algebraic system

Here, it is assumed that the impulse functions (•) k I satisfy I_kx = 0 for all i ∈ I, k ∈ N. The existence and stability of a unique equilibrium state is usually a requirement in the design of artificial neural networks for various applications, particularly when there are destabilizing agents such as delays and impulses. However, even if the unique stable state exists, these agents may affect the convergence speed of the network, which in turn can downgrade the performance of the network in applications that demand fast computation in real-time mode.

Thus, exponential stability is usually desirable for an impulsive network, and sufficient conditions for the global exponential stability of the unique equilibrium state x* of the impulsive network. The impulsive state displacements characterized by Ik : R → R at fixed instants of time t = t_k, k ∈ N are defined by

where dik denote real numbers. This type of impulses has been considered previously in stability investigations of impulsive delayed neural networks [4,6-11,13,21].

For convenience, let

so that the system can be rewritten as

where and the activation functions inherit inheritingsatisfy the properties of

To establish the stability of an impulsive neural network, it has been customary to seek for conditions that govern the network parameters and the impulse magnitude so that both parts – i.e. the continuous-time and the discrete-time equations, of the impulsive network become convergent. Particularly, the requirement imposed on the discrete-time equation as a result of assuming

0 < γ_ik < 1 (or equivalently, 0 < d_ik < 2) has appeared in number of papers studies [4,6-10,13] and references given therein. Although the results provide some insights on the exponential convergence dynamics of impulsive neural networks, their practical use for potential applications of the networks might be limited. Discrete counterparts of continuous-time additive Hopfield- type neural networks with impulses is also investigated by number of researchers in detail [4,7,9,18] and references given therein.

Consider following illustrative example [18]

While the network parameters satisfy existence and uniqueness conditions under appropriate choices of the constants αi > 0, δij, σij∈R and the number p ≥ 1, in order to demonstrate the effect of the impulses towards the convergence of the given systems. Here, we choose μ = 0.4 and see that

Cellular Neural Networks (CNN) is a massive parallel computing paradigm defined in discrete N-dimensional spaces. One can roughly describe basic properties of the (CNN) in the following way:

• A CNN is an N-dimensional regular array of elements (cells);

• The cell grid can be for example a planar array with rectangular, triangular or hexagonal geometry, a 2-D or 3-D torus, a 3-D finite array, or a 3-D sequence of 2-D arrays (layers);

• Cells are multiple input-single output processors, all described by one or just some few parametric functionals;

• A cell is characterized by an internal state variable, sometimes not directly observable from outside the cell itself;

• More than one connection network can be present, with different neighborhood sizes;

• A CNN dynamical system can operate both in continuous (CT-CNN) or discrete time (DT-CNN);

• CNN data and parameters are typically continuous values;

• CNN operate typically with more than one iteration, i.e. they are recurrent networks.

The main characteristic of CNN is the locality of the connections between the units: in fact, the main difference between CNN and other Neural Networks paradigms is the fact that information’s are directly exchanged just between neighboring units. Of course, this characteristic allows also to obtain global processing. Communications between non directly (remote) connected units are obtained passing through other units. It is possible to consider the CNN paradigm as an evolution of Cellular Automata Paradigm. Moreover, it has been demonstrated that CNN paradigm is universal, being equivalent to the Turing Machine.

Like its counterparts Hopfield neural networks and cellular neural networks (CNN) is a massive parallel computing paradigm defined in discrete N-dimensional spaces, each processing unit within a bidirectional associative memory (BAM) network consists of electronic elements such as resistors, capacitors and amplifiers. The finite switching speed of amplifiers has been regarded as a possible factor for causing time delays in the trans- mission of signals among the individual units. Such delays, undoubtedly, can cause in- stability to an otherwise convergent network. To overcome this shortcoming, a number of researchers have incorporated time delays such as discrete delays, variable delays and distributed delays among others into the processing part of the network architecture, and obtained results which can be used for designing the circuit of the delayed BAM network in order to achieve convergence [4,8,20,23,24] and references therein.

It is possible that such convergence could still be affected by another type of destabilization which appears in the form impulsive state displacements. The effects resulting from these impulses can be detected when there are abrupt changes occurring in the voltages of the unit’s states at certain moments of time. If the abrupt changes occur quite frequently with sufficiently large magnitude, then it is possible for the delayed BAM network to lose its convergence. Otherwise, convergence can still be achieved by the network, and this has been reported in a number of investigations on delayed BAM networks that are subject to impulsive state displacements at fixed moments of time [4,6,9,20,].

Following an impulsive BAM network consisting of m processing units on the I - layer and n processing units on the J layer whose neural states

The convergence of a BAM network that is subject to time delays distributed over unbounded intervals and nonlinear impulses with large magnitude towards a unique equilibrium state governed by the systems [24].

Here the analyzes are provided in a unified manner, as such the results yield Lyapunov exponents of the convergent impulsive network. The exponents are typified by a relation involving parameters which are determined from the sufficient conditions governing the network parameters, and also the size of the impulses and the inter-impulse intervals. From these exponents, one can readily establishes special cases the exponential stability of BAM networks with distributed delays and linear impulses of the contraction type, and also the exponential stability of non-impulsive BAM networks with distributed delays.

Consider following discrete class of Hopfield neural networks with periodic impulses and finite distributed delays, which are formulated in the form of a system of impulsive delay differential equations (see more detail [12,13] and references given therein).

where m is the number of neurons in the network, xi(t) is the state of the i-th neuron at time t, ai > 0 is the rate at which the i-th neuron resets the state when isolated from the system, bij is the connection strength from the j-th neuron to the i-th one, gj(.) are the transfer functions, ω is the maximum transmission delay from one neuron to another, cij(.) is the delayed connection strength function from the j-th neuron to the i-th one, di(t) is the ω-periodic external input to the i-th neuron, Z+ is the set of all positive integers, tk ( k ∈z+ ) are the instants of impulse effect, β_ikare constants. Let us assume that:

The solution of the initial value problem (23), (24) is denoted by x (t, ψ). Under the assumption that and k =1, p , making use of the Contraction mapping principle in a suitable Banach space, in [23] it is proved that system (23) is globally exponentially periodic, that is, it possesses a periodic solution x(t, ψ*) and there exist positive constants α and β such that every solution x(t, ψ) of (23) satisfies

In this case each interval [nh, (n + 1) h] contains at most one instant of impulse effect t_k.

Then we have following result

Theorem 3.1: Let system (25), (26) satisfy the conditions H1, H3, H4. Then there exists a number N0 such that for each integer N N0 system (25), (26) is globally exponentially periodic. That is, there exists an N -periodic solution x(n, ψ*) of system (25), (26) and positive constants α and q < 1 such that every solution x(n, ψ) of (25), (26) satisfies

The proof of the result shows that any solution x(n, ψ) exponentially tends to the periodic solution x(n, ψ*) as n → +∞ see more detail [5] and references given therein.

In recent years considerable effort and intensive interest has been shown for the analysis and synthesis of the global asymptotic stability (GAS) and global exponential stability (GES) for the neural networks, as well as the neural approach for solving optimization.

Consider following Hopfield neural networks, described by the nonlinear system:

where x= (x₁, x₂, . . . , x_n)T , and D = dig(d₁, d₂, . . . , d_n) is n × n constant diagonal matrix with diagonal entries di > 0, i = 1, 2, . . . , n and I is the constant external current input to the neuron. The matrix A = Aij is the n × n constant network interconnection matrix. And similarly g(x) = (g₁(x₁), g₂(x₂),..., g_n(x_n))T is a diagonal mapping satisfying the conditions:

The equilibrium x* of the system (34) is said to be globally asymptotically stable; if it is locally stable in the sense of Lyapunov and globally attractive [25,26]. The meaning of global attractivity is every trajectory tend to x∗ as t. The equilibrium x∗ is said to be globally exponential stable if there exist α ≥ 1 and β ≥ 0 such that ∀x0 ∈xR_n ; solution of the system (34) satisfies

This talk covers the general neural networks dynamical systems with various form of the Hopfield type modeling. The results obtained in this paper extend and generalize the corresponding results existing in previous literature. One of the most widely used techniques in the study of models involving ordinary differential equations. It has been shown by several authors that the dynamics of numerical discretization’s of differential equations can differ significantly from those of the original differential equations. In the modelling and analysis of dynamical phenomena various types of systems ranging downward in complexity from partial differential equations, functional differential equations, integra- differential equations, stochastic differential equations with hereditary term, difference equations and algebraic equations have been used. It is common to approximate models of higher levels of complexity by models of lower levels of complexity.

None.

No conflict of interest.

1. S Sitharama Lyengar, EC Cho, Vir V Phoha (2002) Foundations of Wavelet Networks and Applications, Chapman & Hall/CRC, Paris.
2. W Mc Culloch, W Pitts (1943) A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophysics 9: 127-147.
3. JJ Hopfield (1982) Neural networks and physical systems with emergent collective computational abilities. Proc National Acad Sci 79(8): 2554-2558.
4. K Gopalsamy (2004) Stability of artificial neural networks with impulses. Appl Math Comput 154(3): 783-813.
5. JJ Hopfield (1984) Neurons with graded response have collective computational proper- ties like those of two-state neurons. Proc National Acad Sci 81: 3088-3092.
6. H Akca, R Alassar, V Covachev, Z Covacheva, EA Al-Zahrani (2004) Continuous- time additive Hopfield-type neural networks with impulses. J Math Anal Appl 290(2): 436-451.
7. H Akca, R Alassar, V Covachev, Z Covacheva (2004) Discrete counterparts of continuous-time additive Hopfield-type neural networks with impulses. Dyn Syst Appl 13: 75-90.
8. K Gopalsamy, XZ He (1994) Stability in asymmetric Hopfield nets with transmision delays. Physica D 76(4): 344-358.
9. S Mohamad (2000) Continuous and Discrete Dynamical Systems with Applications, Ph. D. Thesis, The Flinders University of South Australia.
10. S Mohamad, K Gopalsamy (2000) Dynamics of a class of discrete-time neural net- works and their continuous-time counterparts. Math Comput Simul 53(1-2): 1-39.
11. X Yang, X Liao, GM Megson, DJ Evans (2005) Global exponential periodicity of a class of neural networks with recent history distributed delays. Chaos, Solutions and Fractals 25(2): 441-447.
12. H Akca, R Alassar, V Covachev, H Ali Yurtsever (2007) Discrete-Time Impulsive Hopfield Neural Networks with Finite Distributed Delays.
13. X Yang, X Liao, DJ Evans, Y Tang (2005) Existence and stability of periodic solution in impulsive Hopfield neural networks with finite distributed delays. Physics Letters A 343(1-3): 108-116.
14. H Akca, V Covachev, Z Covacheva, S Mohamad (2009) Global exponential period- icity for discrete-time Hopfield neural networks with finite distributed delays and impulses. pp. 635-644.
15. K Gopalsamy, KC Issic, IKC Leung, P Liu (1998) Global Hopf-bifurcation in a neural netlet. Appl Math Comput 94(2-3): 171-192.
16. JJ Hopfield, DW Tank (1986) Computing with neural circuits; a model. Science 233: 625-633.
17. S Mohamad, K Gopalsamy (2000) Neuronal dynamics in time varying environments: Continuous and discrete time models. Discrete and Continuous Dynamical Systems 6(4): 841-860.
18. S Mohamad, K Gopalsamy, Haydar Akca (2008) Exponential stability of artificial neural networks with distributed delays and large impulses. Nonlinear Analysis: Real World Applications 9(3): 872-888.
19. H Akca, V Covachev, K Singh Altmayer (2009) Exponential stability of neural net- works with time-varying delays and impulses. pp 153-163.
20. Y Li, L Lu (2004) Global exponential stability and existence of periodic solutions of Hopfield-type neural networks with impulses. Physics Letters A 333: 62-71.
21. P Van Den Driessch, X Zhou (1998) Global attractivity in delayed Hopfield neural networks model. SIAM J Applied Math 58: 1878-1890.
22. Y Li, W Xing, L Lu (2006) Existence and global exponential stability of periodic solutions of a class of neural networks with impulses. Chaos, Solitons & Fractals 27(2): 437-445.
23. Y Li, C Yang (2006) Global exponential stability on impulsive BAM neural networks with distributed delays. J Math Anal Appl 324(2): 1125-1139.
24. S Mohamad, H Akca, Abby Tan, (2008) Lyapunov exponents of convergent impulsive BAM networks with distributed delays.
25. Xu Daoyi, Zhao Hongyong, Zhu Hong (2001) Global dynamics of Hopfield neural networks involving variable delays. Computers & Mathematics with Applications 42(1-2): 39-45.
26. Zhong Shou-Ming, Yang Jin-Xiang, Yan Ke-Yu, Li Jian-Ping (2004) Global asymptotic stability and global exponential stability of Hopfield neural networks. The Proceedings of the International Computer Congress 2004 on Wavelet Analysis and its Applications, and Active Media Technology 2: 1081-1087.