Analytical Description of Fibre Reinforced Sand Shear Strength

Mixing sands with randomly distributed discrete flexible fibers has the potential to increase soil strength and possibly alter their deformation characteristics. Fibre reinforced sand composites of this type are gaining acceptance by engineers as a cost-effective reinforced technique for geotechnical system applications.

Most of the research in this area has focused on the experimental behaviour of the composites ([1-5], among others). Concerning the modelling of the behaviour of fibre reinforced soils, the approaches that have been proposed so far focused on the prediction of the contribution of fibers to the shear strength increase based either on force equilibrium [6-9], energy dissipation [10-12] or superposition of the sand and fibre effects [13] approaches. Recently, a continuum constitutive model based on the rule of mixture of composites has been proposed for both drained and undrained triaxial loading conditions [14-15].

This communication presents an analytical description of the overall stress response at failure (peak strength) of a fibre reinforced sand under the particular case of a direct shear loading. The direct shear conditions are directly applicable to the deformation and sliding of a long slope. An energy-based homogenization technique is used to calculate the failure strength of the fibre-soil composite.

The deformation process of the composite material during shearing involves energy dissipation. The energy dissipation rate during this deformation process in the soil and fibers can be evaluated and this should equate the work rate of the macroscopic stresses.

In the specific case of a direct shear test, the rate of the network input per unit volume of sand/fibre composite (c) of the macroscopic stresses during incremental shear, 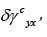and vertical, 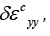strains is:

where are the average horizontal shear and vertical normal stresses, respectively.

Assuming that all of the network input is dissipated in friction [16] - no energy is stored in elastic deformation it is further considered that one part of the work input is absorbed by the sand matrix, 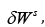and the other part is dissipated at the fibre/grains interface, 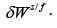Therefore, the fibre-sand interaction process is predominantly frictional in such way that:

With relation (1), then (2) becomes:

If no fibers are present in the composite, relationship (3) reduces to:

where 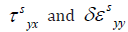would also represent the shear stress and the incremental normal strain, respectively, of an unreinforced equivalent sand matrix system under direct shear conditions. Further developments of (4) should lead to the flow rule as originally proposed by [16]. Assuming that the rate of energy dissipation per unit volume of the soil, 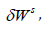the rate of change of horizontal displacement and the thickness of the simple shear zone are all identical in both fibre reinforced and unreinforced specimens, subtracting (4) from (3) and dividing the relationships by 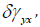one obtains the expression of the shear stress contribution of fiber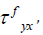s , as:

which considers that

with 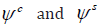representing the dilation angle of the composite and sand, respectively.

If 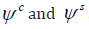are known variables, then the net shear stress contribution of fibers (3) can be predicted once the energy dissipation rate per unit volume due to the interaction between the fibers and the sand matrix,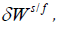, estimated.

The fibers are assumed to be distributed uniformly in space with a random distribution of orientation.

The fibre concentration throughout the entire specimen is defined by:

where V_f represents the volume of fibers and V the volume of the entire specimen.

The fibers are considered to be straight, cylindrical in shape with the length l and radius r. The slenderness of the fibre is described by the aspect ratio η = l / 2r .

In direct shear test, the deformation process is assumed to occur only within the simple shear zone across the sample center with the upper and lower parts of the specimen considered rigid blocks. All the fibers contained in the middle layer are assumed to intersect the shear zone, and as the deformation process advances, the fibers slip and friction between the fibers and the sand will also develop beyond this area. The frictional shear stresses generated between the sand and fibers, 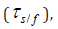is assumed to be uniformly distributed along the fibre and it depends on the magnitude of the stress normal to the fibre surface, 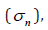and the friction angle of the sand-fibre interface 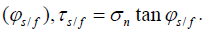. For simplicity, the fibre normal stress, 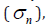is taken to be the same for all the fibers irrespective of their orientation, and equal to the mean of the vertical specimen stress, 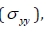and horizontal stresses, 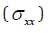and 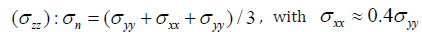σ for direct shear test conditions. However, the amount of the fibers involved in the process is associated with the particular kinematics which develops within the shear zone and it is assumed that only those fibers oriented in the direction of the tensile composite strain will finally contribute to the overall strength increase.

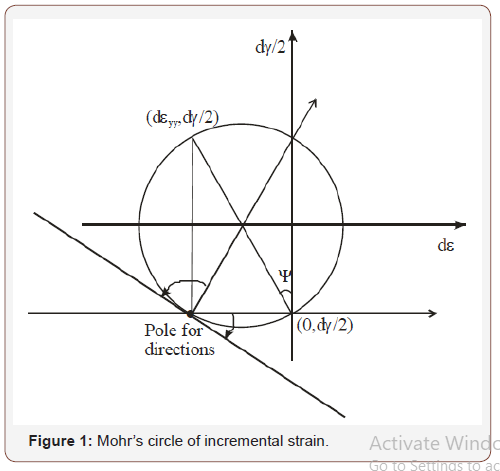
Experimental data presented by [7] on direct shear test showed that at peak stresses, within the deforming shear zone, there was good uniformity of strain, and the horizontal direction was a plane of zero linear extension. Based on this evidence, the Mohr’s circle of incremental strain is constructed (Figure 1) and it can be observed that all the directions between 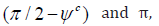represent directions of extension linear incremental strain.

As proposed by [10], a space with ordered fibers can be further introduced; all fibers contained within the middle layer of the specimen are moved in a parallel manner to the origin of that space. In this way, all the fibers are contained by a sphere with radius 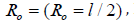Figure 2. Such transformation is admissible since the energy dissipation rate in fibers is dependent only on their orientation, being independent on their location in the sample [10].

The energy dissipation rate due to the slip along its length for a single fibre oriented in the direction α (Figure 2) is:

where δε ^cα is the strain increment along α direction of the fibre-sand composite material given by:

Due to the symmetry of the deformation pattern and random distribution of the fibers, the energy dissipation rate in fibers can be integrated only over one-quarter of the sphere (ABCD, Figure 2) and as the deformation takes place on the (xOy) plane (plane strain deformation), for those fibers located on this vertical plane, l in (8) will be equal to Ro while for all the other fibers, a reduced fibre length with sinγ (Figure 2) will apply, in which case (8) becomes:

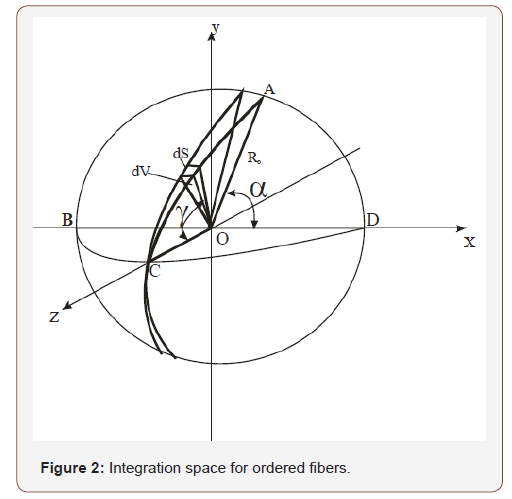
As the number of fibers per unit volume of comp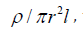osite is the energy dissipation rate in fibers per unit volume of the composite is:

With the infinitesimal volume dV=1/3R_odS (Figure 2 and given notations), and considering (9), (10) and the fact that the regions of fibers in tension and compression are separated by the plane (AOC) of inclination 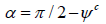(Figure 2), the integration in (11) is performed only over the fibers subjected to tension:

Introducing (13) into (5), the final expression of the shear strength increases due to the contribution of fibers becomes:

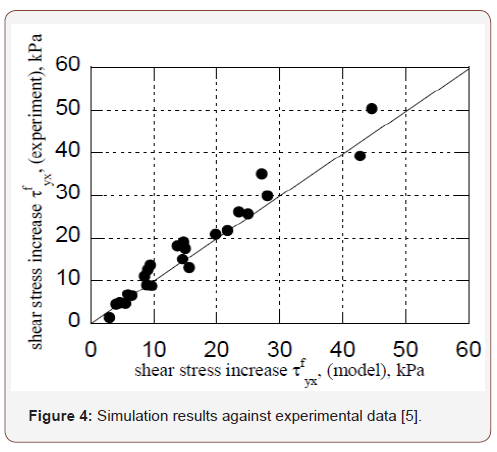
The results provided by relationship (14) are compared with the experimental direct shear data by [5] in Figure 3. Information on sand type, fibers (polypropylene l = 35 mm, r = 0.05mm), test conditions including normal stress, 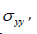fibre concentration are given in [5]. Values of have been considered based on the experimental test results. The friction angle of the sandfibre interface, was assumed to be 18°. As can be observed, the agreement between the experimental results and the values predicted by the model is satisfactory.

An analytical model for fibre reinforced sand peak shear strength in direct shear test conditions has been presented based on an energy-based homogenization technique. The simulated results are in a good agreement

with the experimental results obtained in direct shear tests on sand reinforced with polypropylene fibers. While these developments consider the fibre orientation as randomly distributed, further improvements can be considered in a future work by introducing a fibre orientation function as proposed by [15-18].

None.

No conflict of interest.

1. Al Refeai TO (1991) Behaviour of granular soils reinforced with discrete randomly oriented inclusions. Geotexiles and Geomembranes 10(4): 319-333.
2. Maher MH, Ho YC (1994) Mechanical properties of kaolinite/fiber soil composite. Journal of Geotechnical Engineering Division, ASCE 120(8): 1381–1393.
3. Yetimoglu T, Salbas M (2003) A study on the shear strength of sands reinforced with randomly distributed discrete fibres. Geotextiles and Geomembranes 21(2): 103-110.
4. Tang C, Shi B, Gao W, Chen F, Cai Y (2007) Strength and mechanical behaviour of short polypropylene fiber reinforced and cement stabilized clayey soil. Geotextiles and Geomembranes 25(3): 194-202.
5. Ibraim E, Fourmont S (2006) Behaviour of sand reinforced with fibres. Soil stress-strain behaviour: Measurement, Modelling and Analysis, Solid Mechanics and its Applications 146: 807-818.
6. Gray DH, Ohashi H (1983) Mechanics of fiber reinforcement in sands. Journal of Geotechnical Engineering 109(3): 335-353.
7. Jewell R, Wroth CP (1987) Direct shear tests on reinforced sand. Géotechnique 37(1): 53-68.
8. Maher MH, Gray DH (1990) Static response of sand reinforced with fibres. Journal of Geotechnical Engineering 116(11): 1661–1677.
9. Ranjan G, Vasan RM, Charan HD (1996) Probabilistic analysis of randomly distributed fiber-reinforced soil, Journal of Geotechnical Engineering, ASCE 122(6): 419-426.
10. Michałowski RL, Zhao A (1996) Failure of fiber-reinforced granular soils. J of Geotech Eng, ASCE 122(3): 226-234.
11. Michałowski RL, Čermák J (2002) Strength anisotropy of fiber-reinforced sand. Computers and Geotechnics 29(4): 279-299.
12. Michałowski RL (2008) Limit analysis with anisotropic fibre-reinforced soil. Géotechnique 58(6): 489–501.
13. Zornberg JG (2002) Discrete framework for equilibrium analysis of fibre-reinforced soil. Géotechnique 52(8):593-604.
14. Diambra A, Ibraim E, Muir Wood D, Russell AR (2010) Fibre Reinforced Sands: Experiments and Modelling. Geotextiles and Geomembranes 28(3): 238-250.
15. Diambra A, Ibraim E, Russell AR, Muir Wood D (2011) Modelling the undrained response of fibre reinforced sands. Soils and Foundations 51(4): 625-636.
16. Taylor DW (1948) Fundamentals of soil mechanics. NY Wiley & Sons, pp. 711.
17. Diambra A, Russell AR, Ibraim E, Muir Wood D (2007) Determination of fibre orientation distribution in reinforced sand. Géotechnique 57(7): 623–628.
18. Ibraim E, Diambra A, Russell AR, Muir Wood D (2012) Assessment of laboratory sample preparation for fibre reinforced sands. Geotextiles and Geomembranes 34: 69-79.