 Mini Review
Mini Review
An Understanding The Application Of Helly Theorem For A Topology Of R2
Kyuson Lim*
Department of Mathematics & Statistics, McMaster University, Canada
Kyuson Lim, Department of Mathematics & Statistics, Mc- Master University, Canada.
Received Date: February 21, 2022; Published Date: February 25, 2022
Abstract
In this article, the topological Helly theorem is proven by using Molnar’s theorem and the main theorem from a Helly-type theorem for simple polygons. First, the description of relevant theorem used is introduced. Then, we describe similarities and differences of theorems and theorems are related to prove the goal that the intersection is a simple polygon. The below described is the topological Helly’s theorem.
Introduction
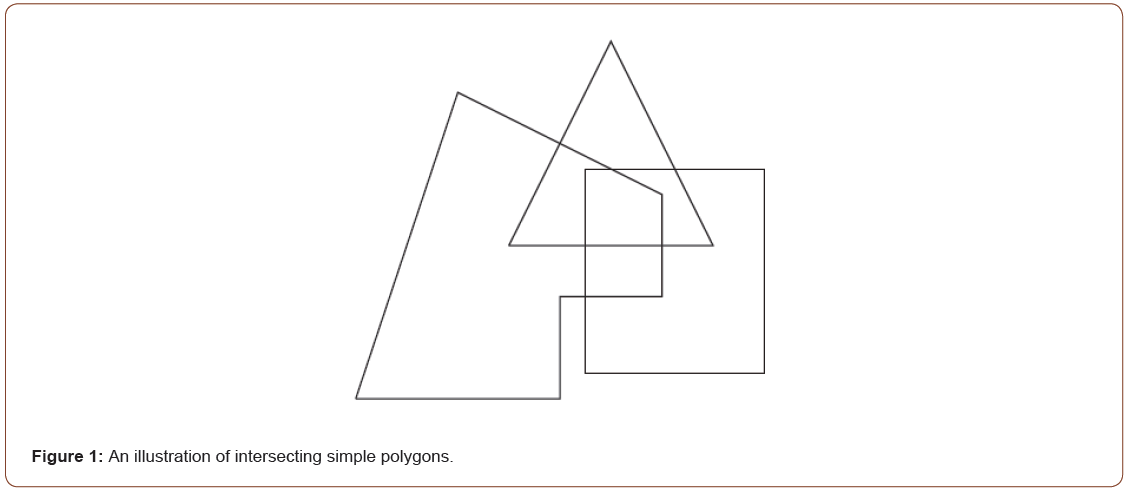
Let  to be simple polygons in the plane. If all double
and triple intersections of Xi are also simple polygons and non
empty, then the intersection of all Xi is also a simple polygon [3]
(Figure 1).
to be simple polygons in the plane. If all double
and triple intersections of Xi are also simple polygons and non
empty, then the intersection of all Xi is also a simple polygon [3]
(Figure 1).
Definition
A simple polygon is defined to be connected without holes, simply connected finite union of convex polygons.
A Description of Theorem
The definition and description are based on “A Helly-type Theorem for simple polygons” and “A Helly-type theorem for Intersections of compact connected sets in the plane” by Marilyn Breen [1,2].
Definition
A planar set S is simply connected if for every simple closed curve λ in S and every point q in the bounded region determined by the λ, q belongs to S (Figure 2).

While the convex set allows only straight lines, the path connected in the simple polygon can be any curves for two distinct points. As simple polygons are not necessarily convex sets, the classic Helly theorem is not applicable. However, we proceed to use compact sets and theorems to show for the intersection of simple polygons.
Theorem: (Molnar’s theorem) If C = {C1...,Cn} is a family of
simply connected compact sets in the plane such that every two (not
necessarily distinct) sets of C have a nonempty intersection, then
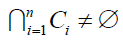 and simply connected.
and simply connected.
Theorem: (98’) ⇔ (the main theorem)
• Every two (not necessarily distinct) sets of C have a connected
union and every three (not necessarily distinct) sets of C have
a simply connected union.
• C is a family of simply connected sets such that every two (not
necessarily distinct) sets of C have a connected intersection and
every three (not necessarily distinct) sets of C have a nonempty
intersection.
Part (1) implies (2) using Lemma 1 and Lemma 2. Part (2) implies (1) using Proposition 1 applied by the Lemma 3.
a. Lemma 1: Let C1 and C2 to be compact connected sets in the
plane. If C1 ∪C2 is simply connected.
b. Lemma 2: For C1, C2, C3 nonempty compact connected sets
in the plane, if every two of these sets have a connected
union and all three sets have a simply connected union, then
C1 ∩C2 ∩C3 ≠ ∅.
c. Lemma 3: Let λ be a simple closed curve in the plane, with
point q in the bounded region determined by λ and point r in
the unbounded region determined by λ.
Let μ1, μ2, μ3 be simple closed curves from q to r, with λ ∩μi finite for 1≤ i ≤ 3 and λ ∩μi ∩μj ≠ ∅ , for 1≤ i ≤ j ≤ 3 . Then, for some point b1 ∈μ1 ∩λ is in a bounded region determined by μ2 ∪μ3
In summary, for three different closed curve connecting points q∈λ to r we are able to find a point b1 that is the intersection of μ1 and λ bounded inside the connected region of λi ∪λj . Note that the point bi from λ ∩μi does not belong to λ ∩μi ∩μj ≠ ∅ . This means there are three cases to find the point bi from μi ∩λ defined in μ2 ∪μ3 or μ2 ∩λ defined in μ1 ∪μ3 or μ3 ∩λ defined in μ1 ∪μ2
d. Proposition 1: For family of set C of n ≥ 2 in the plane, if
every two sets of C have a connected, simply connected union and
 is simply connected.
is simply connected.
The goal of Proposition 1 with Lemma 3 is to show for three sets with Part (2) to be simply connected union of Part (1).
Theorem: (An intersection theorem)
Let P be the family of simply polygons P1,…, Pn in the plane. If
every three (not necessarily distinct) polygons of P have a simply
connected union and every two polygons of P have a nonempty intersection,
the 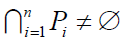 .
.
The intersection theorem could not directly apply to simple polygons to derive a common intersection as every three polygons are simply connected union for a given condition.
A Relationship of Theorem
Difference
While the Molnar’s theorem applicable for compact connected sets and an intersection theorem is applicable for simple polygons. Generally, simple polygons in the plane are identified to be compact connected sets.
While the Molnar’s theorem is conditioned for triple intersection of sets to be nonempty, the intersection theorem is conditioned for triple sets to be simply connected union.
In the Molnar’s theorem,  is simply connected, the intersection
theorem does not support
is simply connected, the intersection
theorem does not support 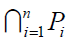 to be simply connected.
to be simply connected.
Similarity
Using the induction, both theorems resulted in the common intersection of finitely many sets to be non-empty. Note that the intersection theorem is a strong version of theorem 1 with the same conclusion for Molnar’s theorem of common intersection for finitely many sets.
With loss of generality, the intersection theorem where all triples polygons have simply connected union is stronger than Part (2) with a condition that all triple sets of intersection is nonempty.
Corollary
Based on the Molnar’s theorem and theorem 1 of part (1),
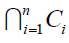 is nonempty, connected and simply connected and
is nonempty, connected and simply connected and
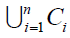 is simply connected.
is simply connected.
Basis
The conclusion that  , is supported by the Molnar’s
theorem as
, is supported by the Molnar’s
theorem as  is nonempty, simply connected, which is
based on the induction. However,
is nonempty, simply connected, which is
based on the induction. However, 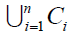 is connected, simply connected
is supported by the theorem 1 of part (1) for induction with
proposition 1 to be applied with.
is connected, simply connected
is supported by the theorem 1 of part (1) for induction with
proposition 1 to be applied with.
Consequence
This corollary proves that 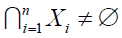 , is a finite union of
convex sets for simple polygons of X1,…,Xn. This fact that
, is a finite union of
convex sets for simple polygons of X1,…,Xn. This fact that 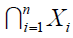 is a simple polygon is supported by the corollary only for the basis
of main theorem and Molnar’s theorem where a simple polygon consists
of finite union of convex polygons.
is a simple polygon is supported by the corollary only for the basis
of main theorem and Molnar’s theorem where a simple polygon consists
of finite union of convex polygons.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Breen M (1998) A Helly-type theorem for intersections of compact connected sets in the plane. Ge-ometriae Dedicata 71(2): 111-117.
- Breen M (1996) A Helly-type theorem for simple polygons. Geometriae Dedicata 60(3): 283-288.
- Pak I, Wilson S (2013) A quantitative Steinitz theorem for plane triangulations. arXiv preprint arXiv, 1311.0558.
-
Kyuson Lim. An Understanding The Application Of Helly Theorem For A Topology Of R2. Glob J Eng Sci. 9(1): 2022. GJES. MS.ID.000708.
-
Helly theorem Molnar's theorem, polygons, simply connected union
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






