A Strategy With Master-Slave Mechanism Dominates in Spatial Iterated Prisoner’s Dilemma

The Prisoner’s Dilemma is a two-player non-zero-sum game in which two players try to maximize their payoffs by cooperating with or betraying the other player. In the classical version of prisoner’s dilemma, each player chooses between two strategies, Cooperate (C) and Defect (D). Their payoffs can be represented by the matrix shown in Figure 1.

In the payoff matrix, R, S, T, and P denote Reward for mutual cooperation, Sucker’s payoff, Temptation to defect, and Punishment for mutual defection respectively, and T > R > P > S. The constraint motivates each player to play non-cooperatively [1,2].

In the Iterated Prisoner’s Dilemma (IPD), two players have to choose their mutual strategy repeatedly, and they also have memory of their previous behaviors and the behaviors of the opponents. There is R > 1/2(S +T), which is set to prevent any incentive to alternate between cooperation and defection.

Axelrod started studying efficient IPD strategies by means of competitions and found the winner of his competitions, Tit For Tat (TFT) [3,4]. TFT always cooperates in the first move and then mimics whatever the opponent did in the previous move. According to Axelrod, several characteristics make TFT successful: TFT is Nice, Retaliating and Forgiving. Since then, researchers are attempting to develop novel strategies that can outperform TFT either in roundrobin tournaments or in evolutionary dynamics.

A strategy with a simple identification mechanism, named ‘handshake’ [5-8], appeared in evolutionary IPD. This strategy defects at the first move and cooperates on the second move. If the opponent behaves in the same way, it will keep cooperating in the following moves. Otherwise, it will always defect. By means of a mechanism like ‘handshake’, a group of strategies are able to recognize each other and then behave collectively [7-11].

In this paper, we show that a novel strategy, which we call it Collective Strategy with Master-Slave Mechanism (CSMSM), dominates in spatial IPD. CSMSM outperforms other IPD strategies when they form clusters. Simulation results show that CSMSM always outperforms non-collective opponents once they form a cluster in the initial population.

Based on handshaking, a group of strategies can recognize each other and deal with group members and non-members differently.A handshake in IPD is a predefined sequence of moves for two interacting players. If both players play the same sequence of moves, they recognize each other as group members. Otherwise, they identify the opponent as non-kin.

In this paper, the handshake of CSMSM is a sequence of ‘CDCCD’. When two CSMSMs meet, they will play this sequence in the first five moves and then recognize each other as a group member. If the opponent has played a different sequence, this immediately triggers defection and a CSMSM will always defect against the opponent from that point on.

As long as two CSMSMs have identified each other, they will play either a master or a slave role. Every CSMSM behaves as a master originally. In each generation, a master CSMSM may change to a slave with a predefined probability, which makes sure that there is always a ratio of slaves in the CSMSM group. A slave will always be a slave. Because the slaves are designed to sacrifice them in order to maximize the masters’ payoffs, they are likely to receive lower payoff than the average of the population and then they die out in each generation. Thus, the percentage of slaves in CSMSM will be approximately 70% when the probability of a master changing to a slave is set to be 0.7.

As long as two CSMSMs have identified each other, a master will act as a Grim trigger (it chooses ‘C’ as long as the opponent chooses ‘C’. Once the opponent has chosen ‘D’, it always defects) and a slave will act as a reverse TFT (it chooses ‘D’ first and then chooses the reverse of the opponent’s previous choice). When a master and a slave meet, the master chooses ‘C’ and the slave chooses ‘D’ in the sixth move, and then the master will always play ‘D’ and the slave will always play ‘C’ so that the master’s payoff in the following rounds is maximized.

When two masters meet, they will cooperate with each other except handshaking in the first five moves. When two slaves meet, they will play a sequence of alternate defection and cooperation after handshaking.

As an example, let’s consider how a CSMSM interacts with a TFT. Both strategies play ‘C’ in the first move. Then TFT plays ‘C’ and CSMSM plays ‘D’ in the second move. Since TFT has not played the handshaking sequence, CSMSM will play ‘D’ thereafter. They will keep defecting after the third move.

When CSMSM forms a cluster in the population, they outperform any individual strategy. In the next section, we analyze the performance of CSMSM in spatial IPD game.

As a collective strategy, the performance of CSMSM in a spatial IPD depends on the size of the clusters they form. Whenever CSMSM has formed a cluster of significant size, they will outperform their competitors.

CSMSM vs TFT

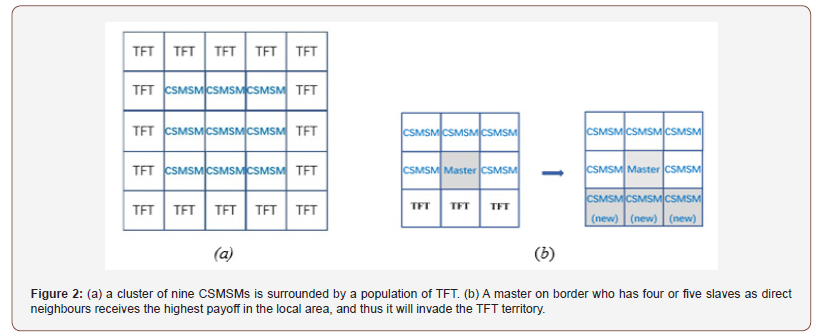
Let’s first consider a typical scenario that a cluster of nine CSMSM is surrounded by TFTs, as shown in Figure 2a. The minimum size of a cluster for CSMSM to survive in a population of TFT is nine. Let n (n>6) denote the number of iterations in the IPD.

A TFT receives R+(n-2)P+S in interacting with a CSMSM and receives nR against another TFT. A master CSMSM receives T+R+(n-2)P against a TFT, (n-2)R+2P against a master, and (n-6) T+3R+2P+S against a slave.

Without self-interaction, each strategy plays eight IPDs with its direct neighbours. A TFT may have zero, one, two, or three CSMSM neighbours depending on its position. With zero CSMSM and eight TFT neighbours, a TFT receives T₀ = 8nR payoff. With one, two, or three CSMSM neighbours, the payoff of a TFT is T₁ = 7nR +(R+(n- 2)P+S), T₂ = 6nR +2×(R+(n-2)P+S), or T₃ = 5nR +3×(R+(n-2)P+S) respectively. There are T₁ >T₂ >T₃ since R >P >S.

For CSMSM, we only need to consider the payoffs of the masters because the slaves generally receive lower payoffs than TFTs. Depending on the position of a master, it may have three, five, or eight CSMSM neighbours.

a) First, let’s consider the scenario that the center of the cluster of nine CSMSM is a master. Let m (8≥ m ≥0) denote the number of slaves in the cluster. The payoff of the master can be computed by C0 = m((n-6)T+3R+2P+S)+(8-m)((n- 2)R+2P). We have

when n 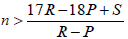and whatever value of m is. The payoff of the central master is the highest within the 5x5 area when the number of iterations is long enough, for example n>16 when R=3, P=1, S=0. Thus, the cluster of CSMSM cannot be invaded by TFT if the central strategy is a master.

b) Second, let’s consider the scenario that a master is located on one side border of the cluster (with five CSMSM neighbours). Let l (5 ≥ l ≥0) denote the number of slaves in the five CSMSM neighbours. The payoff can be computed as C1 = l((n-6)T+3R+2P+S)+(5-l) ((n-2) R+2P)+3×(T+R+(n-2)P). In order that C₁ > T₀, we have

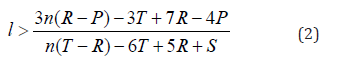
In the case that T=5, R=3, P=1, S=0 and n=50, (2) can be computed as l>3.55. It means that the master receives greater payoff than the highest payoff of TFT if l=4 or 5. The three TFT neighbours will be replaced by CSMSM, as shown in Figure 2b.

In the case that n is far greater than T, n>50 for example, (2) can be simplified to (3).

Under the condition of (2) or (3), the cluster of CSMSM grows in size.

In the case that T₀ > C₁ > T₁, we have,

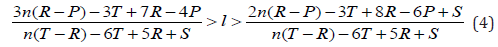
It can be simplified to (5) when n is a relatively large value.

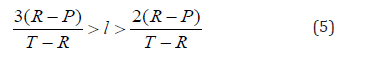
Under the condition of (4) or (5), the payoff of the master is higher than its TFT neighbours and lower than the highest payoff of TFT. Thus, the cluster of CSMSM will maintain the current size.

c) Third, when a master locates on one corner of the cluster (with three CSMSM neighbours), the payoff is C₂ = q((n-6) T+3R+2P+S)+(3-q)((n-2)R+2P)+ 5×(T+R+(n-2)P), where q (3 ≥ q ≥0) is the number of slaves in the three CSMSM neighbours. It can be verified that C2 is always smaller than T₂ . Thus, a master on the corner always receives lower payoff than its TFT neighbours.

In summary, if there is a master on the border and the number of its slave neighbours satisfies (2) or (3), the neighbour TFTs will be replaced by CSMSM and the cluster of CSMSM grows. Otherwise, if the center of the cluster is a master, or there is a master on the border and (4) or (5) satisfies, the cluster will maintain the current size. In other situations, the cluster of CSMSM may be invaded by TFT.

In the case that T=5, R=3, P=1, S=0 and n=50, the ratio of slaves in CSMSM should be at least 30% so that there are approximately three slaves in the neighbourhood of a master on border, which makes sure that the border cannot be invaded by TFT. If the ratio of slaves can be maintained higher than 30%, CSMSM outperforms TFT in spatial IPD.

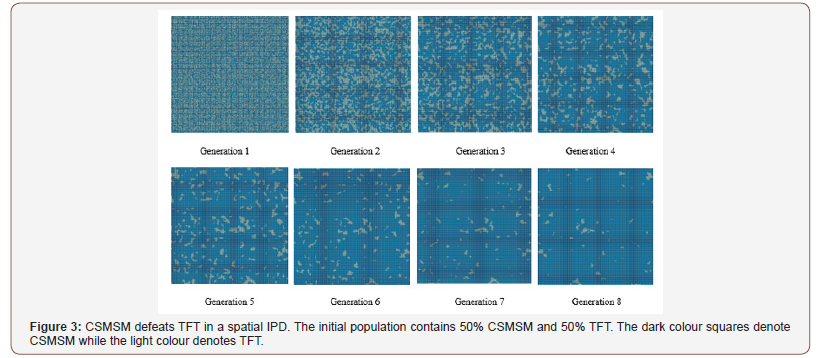
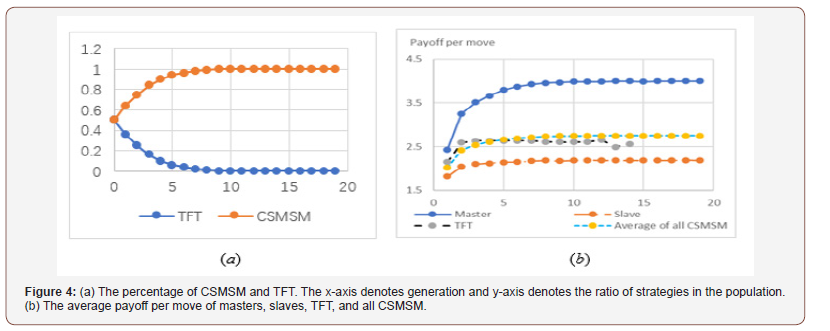
The result of a simulation of CSMSM competing against TFT is shown in Figure 3, where the initial population is 50% TFT and 50% CSMSM, randomly allocated on a 200×200 grid. The changes of the percentages of two strategies in the population and average payoffs are illustrated in Figure 4(a) and (b) respectively. It shows that the masters outperform TFT decreases rapidly and it dies out after 13 generations (Figure 3&4).

SMSM vs AllD

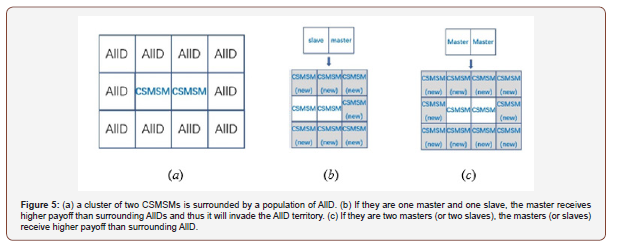
surrounded by AllDs, as shown in Fig. 5a. Each CSMSM has seven AllD and one CSMSM neighbours. An AllD may have zero, one, or two CSMSM neighbours (Figure 5).

An AllD receives T+(n-1)P in interacting with a CSMSM and receives nP against another AllD. A master CSMSM receives (n-1)P+S against an AllD, (n-2)R+2P against a master, and (n-6) T+3R+2P+S against a slave. A slave receives (n-1)P+S against an AllD, T+3R+2P+(n-6)S against a master, and (nR+nP)/2 against a slave.

With zero, one, and two CSMSM neighbours, the payoff of an AllD are 8nP, 7nP +(T+(n-1)P), and 6nP +2×(T+(n-1)P) respectively. The greatest of three values is D2 = 8nP+2T-2P.

If two CSMSMs are a master and a slave, the master receives 7×((n-1)P+S)+ ((n-6)T+3R +2P+S) and the slave receives 7×((n-1) P+S)+ (T+3R+2P+(n-6)S). The payoff of the master is higher than D2, the highest payoff of AllD, when there is

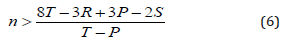
In the case that T=5, R=3, P=1, S=0 for example, there is n > 8.5. Under this condition, the AllD neighbours around the master will be replaced by CSMSM, as shown in Figure 5b.

If both CSMSMs are masters, their payoff is 7×((n-1)P+S)+ ((n-2)R+2P) and it is higher than D2 when (6) is satisfied. If both CSMSMs are slaves, their payoff is 7×((n-1)P+S)+ (nR+nP)/2 and it is higher than D2 as well. Thus, the AllDs in the neighbourhood of the two CSMSMs will be replaced, as shown in Figure 5c. Thus, a cluster of two or more CSMSM outperforms AllD in spatial IPD.

CSMSM invades a population of another strategy

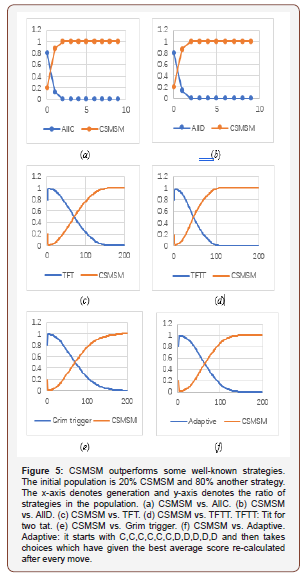
We have simulated CSMSM competing against some wellknown strategies in spatial IPD. The results are given in Figure 6. The initial population in each simulation contains 20% CSMSM and 80% another strategy, randomly mixed and allocated on a 200×200 grid. In all simulations, CSMSM outperforms the opponent strategy in 200 generations.

For some naive strategies like AllC, AllD, and Random player, CSMSM expels them in 3-5 generations because it does not need clusters of significant size to invade the territory of those strategies.

We have presented a CSMSM strategy that outperforms well-known strategies such as TFT in spatial IPD. By means of a handshaking and a master-slave mechanism, CSMSM manages to maximize the masters’ payoffs and minimize the opponents’ payoffs. Spatial IPD simulations show that CSMSM outperforms non-collective strategies even if it is minority in the initial population. Once CSMSM has formed a cluster of significant size, it will dominate in the evolution as a result.

Existence of strategies like CSMSM suggests that cooperation first appears in a group of agents who cooperates with group members and defects against non-members. Once those agents form a small cluster, they outperform defective neighbours and their percentage grows steadily in the population.

None.

No conflict of interest.

1. J Nash (1951) Non-cooperative Games. The Annals of Mathematics 54(2): 286-295.
2. S Chong, J Humble, G Kendall, J Li, X Yao (2007) Iterated prisoner’s dilemma and evolutionary game theory. In: The iterated prisoners’ dilemma: 20 years on. Singapore: World Scientific. Advances in Natural Computation 4: 23-62.
3. R Axelrod (1984) The Evolution of Cooperation. BASIC Books, New York./li>
4. R Axelrod (1980) Effective choice in the prisoner’s dilemma. Journal of Conflict Resolution 24(1): 3-25.
5. J Li (2007) How to design a strategy to win an IPD tournament. in G Kendall, X Yao and S Chong (eds) The iterated prisoner’s dilemma: 20 years on. World Scientific 4: 89-104.
6. J Li, G Kendall, R John (2015) Computing Nash Equilibria and evolutionary stable states of evolutionary games. IEEE Transactions on Evolutionary Computation 20(3): 460-469.
7. J Li, G Kendall (2009) A strategy with novel evolutionary features for the iterated prisoner’s dilemma. Evolutionary Computation 17(2): 257-274.
8. A Robson (1990) Efficiency in evolutionary games: Darwin, Nash, and the secret handshake. Journal of Theoretical Biology 144(3): 379-396.
9. M Doebeli, C Hauert (2005) Models of cooperation based on the Prisoner's Dilemma and the Snowdrift game. Ecology Letters 8(7): 748-766.
10. D Ashlock, E Kim, W Ashlock (2009) Fingerprint analysis of the noisy prisoner’s dilemma using a finite-state representation. IEEE Trans on Computational Intelligence and AI in Games 1(2): 154-167.
11. A Rogers, R Dash, S Ramchurn, P Vytelingum, N Jennings (2007) Coordinating team players within a noisy iterated Prisoner’s Dilemma tournament. Theoretical Computer Science 377(1-3): 243-259.