 Review Article
Review Article
Usage of Optimization Techniques in Civil Engineering During the Last Two Decades
Tayfun Dede1*, Moacir Kripka2, Vedat Togan3, Victor Yepes4 and R Venkata Rao5
1,3Department of Civil Engineering, Karadeniz Technical University, Turkey
2Department of Civil Engineering, Universidade de Passo Fundo, Brazil
4ICITECH (Institute of Concrete Science and Technology). Department of Construction Engineering, Universidad Politécnica de Valencia, Spain
5Department of Mechanical Engineering, Sardar Vallabhbhai National Institute of Technology, India
Tayfun Dede, Department of Civil Engineering, Karadeniz Technical University, Turkey.
Received Date: March 25, 2019; Published Date: April 15, 2019
Abstract
In the real world, there are many problems in which it is desirable to optimize one or more objective functions at the same time. These are known as single and multi-objective optimization problems respectively and continuous research is being conducted in this field and nature inspired heuristic optimization methods (also called advanced optimization algorithms) are proving to be better than the classical deterministic methods and thus are widely used. These algorithms have been applied to many engineering optimization problems and proved effective for solving some specific kinds of problems. In this paper, a review of the most popular optimization algorithms used in different problems related to the civil engineering during the last two decades is presented. It is hoped that this work will be useful to researchers involved in optimization.
Keywords:Optimization algorithms; Civil engineering; Review
Introduction
Optimization problem is defined as finding the best solution from the feasible solution in a pool which contains all solutions. In many engineering problems, the optimal solution can be the minimum or maximum value of the objective function of the problem. Sometimes, the optimization problem might have multiple objective functions and multiple solutions. Also, the optimization problems can be classified as size, shape, and topology, discrete, continuous, single or multi-objective optimization. The application of optimization to real word engineering problems is quite recent, mainly due to the complexity of mathematical models, described by non-linear functions and generating a non-convex space of solutions. With the advent of advanced optimization methods, last decades have witnessed a growing application of optimization to a wide range of engineering problems, from automotive to biomedicine, and of course, to civil engineering. Applications of optimization techniques are most exciting, challenging, and of truly large scale when it comes to the problems of civil engineering in terms of both quality and quantity. In order to overcome the difficulties, researchers are interested in advanced optimization techniques. In the recent literature, researchers have applied the advanced optimization techniques to different purposes. The aim of this paper is to collect the studies using optimization algorithms in different divisions of civil engineering problems in such as structural engineering, construction management, mechanics, transportation and geotechnical engineering. This paper consists of two main sections. The first one is the optimization algorithms which have been used to solve civil engineering problems. The other one is the application of the optimization algorithms on different divisions of the civil engineering problem presented in last decades. Then, the conclusions and the references are given as last sections.
Optimization Algorithms
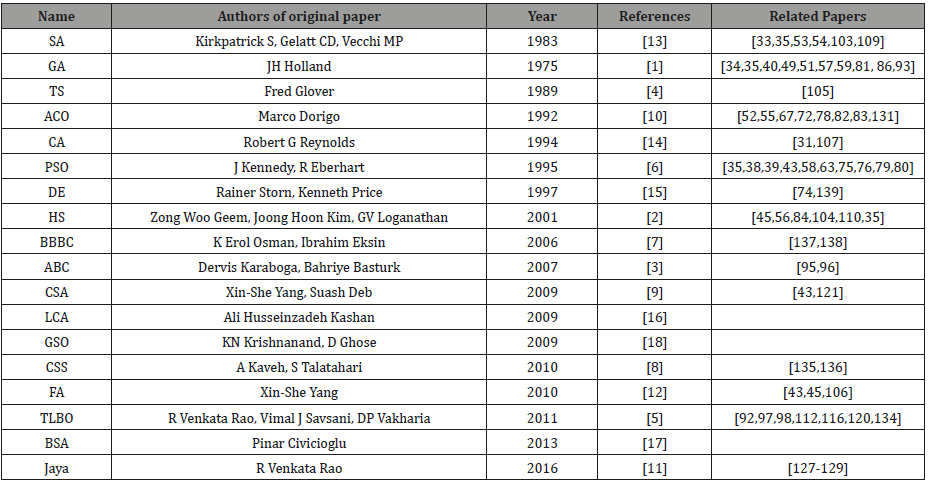
The optimization algorithms have been introduced in this section. These algorithms are; Genetic Algorithms (GA), Harmony search (HS), Artificial Bee Colony (ABC), Tabu Search (TS), Teaching– Learning-Based Optimization (TLBO), Particle Swarm Optimization (PSO), Big bang – big crunch (BBBC), Charged System Search (CSS), Cuckoo Search Algorithm (CSA), Ant Colony Optimization (ACO), Jaya, Firefly algorithm (FA), Simulated Annealing (SA), Cultural Algorithm (CA), Differential Evolution (DE), League championship algorithm (LCA), Backtracking Search Algorithm (BSA),Glowworm Swarm Optimization (GSO), Memetic Algorithm (MA), Greedy Randomized Adaptive Search Procedure (GRASP), etc. In addition to these algorithms, similar algorithms derived from these algorithms have been developed by the researchers such as elitist TLBO and intelligent GA. In the multi-objective optimization problem, the name of the existing optimization algorithm may be changed as NDS-GA (non-dominated sorting genetic algorithm). In the Table 1, the optimization algorithm and their first original papers are given. Genetic algorithms based on the Darwin’s theory about evolution [1]. These algorithms start with a randomly generated initial population which is a set of possible solutions related to the problem. In each generation of the optimization process, the biological operators are used to create next population by the hope that the new population will be better the old one. The main operators used in this algorithm are selection, encoding, crossover and mutations. The new solutions are selected from the current populations according to their value fitness functions (Table1).
Table:Optimization algorithms.
Harmony search was firstly proposed in the dissertation by Geem [19], then presented in a journal paper by the Geem et al. [2]. It is derived from an artificial phenomenon found in musical performance namely the process of searching for better harmony. Musical performances seek a best state determined by aesthetic estimation, as the optimization algorithms seek a best state determined by objective function evaluation. This algorithm stars an initial harmony memory (solutions sets) and used some parameter such as harmony memory considering rate (HMCR) to improve the next harmony memory. Artificial Bee Colony simulates the intelligent foraging behavior of honey bee swarm. Employed bees, unemployed bees, and scout bees are the type of bee defined in this algorithm. Employed bees search food around the food source and they store the nectar. Unemployed bees choose the source of food with certain probability by following the dances of the employed bees. The unemployed bees turn to the source of the selected food and begin to store nectar as employed bees. Employed bees who consume food sources become scout bees to search for new sources [20]. Tabu Search algorithm explores the search space by a sequence of movies. To escape the local optimum, the certain movies are listed in a memory called forbidden (tabu) search. This algorithm contains some elements: tabu list, neighborhood, aspiration criterion, termination criterion and cost function. Among from these elements, the aspiration criterion is used to determine the best search movie. The new solutions are chosen from the neighborhood of the current solution and the solution which has the minimum cost becomes the new current solution [21]. Teaching–Learning-Based Optimization consists of two phases: Teacher Phase and Learner Phase. In the first phase, the best solution which has the minimum objective function is defined as a teacher. By using the mean solution and the teaching factor, the new solutions are created in the neighborhood of the teacher. If the new solution is better than the old one, the new solution is replaced with the old one. In the learner phase, the solutions obtained from the learner phase are called as student. Randomly select two students are compared with each other. The new solution is created in the neighborhood of the better student. In this way all students are compared to each other. The new solution obtained from the learner phase is replaced the old one if it is better than the old one. So, the solutions are updated in the TLBO algorithm to find global solution [22]. Particle Swarm Optimization is an optimization method based on the using a population of particles to find the optimal solution [6,23]. In this algorithm, swarm is consisted of particles which are the individuals (feasible solutions). This algorithm does not require derivative information and has an easy implementation in searching the optimal solutions. To find best position (optimal solutions) each particle cooperates with each other by moving according to their velocity [24].
Big Bang–Big Crunch uses a randomly created initial population as in the other population-based optimization algorithms. Initial population is called Big bang phase in this algorithm. The individuals (candidate solutions) of Big bang phase are dispersed to the search space in a uniform manner [7]. The other phase is the Big Crunch for this algorithm. This phase has a convergence operator to obtain only one output from the feasible inputs. After the implementation of these phases, the new population is created to find optimal solutions. Charged System Search is a populationbased optimization method. It is established on the physics laws. Each solution sets are considered as a charged particle. This particle is affected by the electrical fields of the other agents. Each particle has a magnitude of charge and as a result creates an electrical field around its space. The magnitude of the charge is calculated according to the quality of its solution [8,25]. This algorithm uses a memory to save a number of first charged particles and their values of objective functions. This memory is called as charged memory. The updated charged particles are compared with the old ones, and the better ones are stored in the charged memories [26]. The procedure is repeated by the hope that the optimal solutions will be reached. Cuckoo Search Algorithm is based on the obligate brood parasitic behavior of some cuckoo species in combination with the Levy flight behavior of some birds and fruit flies [9]. There are three rules to implement this algorithm: each cuckoo lay one egg at a time and dump its egg in randomly chosen nest. The egg in a nest represents a solution and cuckoo egg represents a new solution for the process of the optimization problem. Like the other methods, the best solution (best nest) is transferred to the next generations. The number of available host nests is fixed, and the egg laid by a cuckoo is discovered by the host bird with a probability. Ant Colony Optimization mimics the behavior of ants to find shortest paths between their colony and food sources. The main parameters of this algorithm are: ant, pheromone, daemon action, and decentralized control. The pheromones are dropped by the ants traveling for food. The path marked by the high intensity of the trail which is the global memory of the system is chosen by ants. Daemon actions are used to gather global and the decentralized control is used in order to make the algorithm robust and flexible within a dynamic environment [10,27].
Jaya is a new optimization algorithm. This algorithm starts an initial randomly created population (feasible solution sets). The best and the worst solutions are determined based on the objective function. The new individuals (solution) are generated in the neighborhood of the best solution by avoiding the worst solution. The implementation of this algorithm is so easy. The algorithm strives to become victorious by reaching the best solution and hence it is named as Jaya (a Sanskrit word meaning victory) [11]. Firefly algorithm is based on the idealized behavior of the flashing characteristics of fireflies [12]. In nature, the firefly flashes as a signal to affect the others firefly. In FA, this natural phenomenon of firefly is formulated as a meta-heuristic algorithm depending on following three rules [28,29]: 1-All fireflies are affected by each other without respect to their sex.2- Attractiveness is proportional to its brightness. 3- If there are no brighter fireflies than a particular firefly, it will move randomly in the space. The light absorption coefficient the randomization control factor and the size of population are the main control parameter of this algorithm. Simulated Annealing mimics the random behavior of molecules during an annealing process, which involves slow cooling from a high temperature [13,30]. SA starts an initial solution called parent. This parent is updated by some manner in the optimization process to set of offspring. Among the offspring the best one can be a candidate to challenge its parent. According to the objective function, if the candidate is better than its parent, the parent is replaced by the candidate. That is, the candidate has a minimum value of objective function. Thus, the best solution is always kept along the optimization process. Cultural Algorithm is inspired by the principle of cultural evolution. A set of traits and generalized description of individual’s experiences are used to describe the individuals. There are some parameters such as outlining, dominant belief, acceptance and selection to update the individual for the next generation in CA [14]. For example, through an acceptance function, the experiences of individuals in the population space are used to generate problem solving knowledge that is to be stored in the belief space [31]. Differential Evolution is a parallel direct search [15]. Like the other evolution algorithms, DE uses an initial population. There are two main components in the optimization process of CA: mutation and crossover. Through mutation operator DE generates new parameter vectors by adding the weighted difference between two population vectors to a third vector. Parameter mixing is called as crossover. The feasible solution is generated by two components for the next generation.
League championship algorithm is based on the championship process in a sport league. The terms “league” represents the population, “team” represents the individual, “team formation” represents a solution, “week” represents the iteration, and “playing strength” represents the value of objective function in the process of the optimization problem [16]. In LCA, there are six rules to implement the algorithms. Like other population-based algorithms. This algorithm uses an initial process ad update the population in each week to reach the optimal solutions. Backtracking Search Algorithm have five main components to find optimal solutions. These are initialization, selection-I, mutation, crossover and selection-II [17]. In the initialization phase, the size and dimensions of the optimization problem are created. Selection-I phase determines the historical population using the memory. Initial and final form of the trial population is generated by the mutation process and crossover process, respectively. In the Selection-II phase, the best individual is accepted as global solution if its value of objective function is better than the one obtained throughout optimization process. Glowworm Swarm Optimization mimics the behavior of glowworms which are represented by a feasible solution set (individual of population). These are randomly placed in the solution space [18,32]. Glowworms contain a luminescent quantity called luciferin. The intensity of luciferin determines the value of the objective function of the optimization problem. So, the individual with highest density of luciferin can be defined as the best solution in GSO. In GSO, the glowworms are in interaction with their neighbors and move toward the brighter glowworm using a probabilistic mechanism. According to the value of the objective function, the individuals are updated to create new individuals by the hope that to find global solutions.
Application of Optimization Algorithm for Civil Engineering Problems
In this section, the literature review related to the optimization problems on the different divisions of the civil engineering in last decades is presented. These problems are categorized as Structural, Mechanical, Hydraulics, Construction Management, Transportation, and Geotechnical.
Optimization in geotechnical problems
Optimization problem was carried out in many fields of geotechnical engineering such as, earth-retaining walls, reinforced concrete shear-walls, and slope stability prediction. The studies presented in recent years using different optimization algorithms for this field are given below. Yepes et al. [33] presented a parametric study on optimization of earth-retaining walls. They used SA algorithm to optimize the walls from 4 to 10 m in height for different fills and bearing conditions. The design variables of their problem are the geometrical properties of the wall, material types and the reinforcement set-up. The cost function is considered as the objective function. In the structural analysis of the wall overturning, sliding and ground stresses are taken into account as structural limit. Their study estimates the relative importance of factors such as the limitation of kerb deflections and base friction coefficient. At the end of their study, the authors reported the upper bound of 50 kg/m3 of reinforcement in the kerb and 60 kg/m3 for the overall wall. Atabay [34] used the GA to optimize 3D-dimensional beamless reinforced concrete shearwall systems. In this study, the total material cost function is used as the objective function and constraints of structural optimization problem are taken into account according to the requirements of the reinforcement concrete specification (TS500) and the seismic code of Turkey which is put into effect on 1998. Structural system is analyzed by GENOPT which was developed by the author. By using this program, 13-floored beamless structure was optimized. In the conclusion of the study, the author stated that the GENOPT not only valid for the cost optimization of shear-wall reinforced concrete structure sys but also is valid for the many reinforced concrete structure systems. Pei & Xia [35] presented a study on the design of reinforced cantilever retaining walls using heuristic optimization algorithms which are the genetic algorithm (GA), particle swarm optimization (PSO) and simulated annealing (SA). The constraints of this optimization problem are the design requirements and geometrical constraints. To carry out the optimization process 25 constraints are established, and 9 parameters are selected by the authors. The objective function of the problem is the cost function of the cantilever retaining wall including the cost of concrete and reinforcement per linear meter. This study was previously presented in the International Conference on Structural Computation and Geotechnical Mechanics in 2012.
Hosseinzadeh & Joosse [36] reported the design optimization of the retaining walls in narrow trenches. The authors developed an environmentally-friendly method for economic design and optimization of retaining wall. Their study includes both analytical and numerical methods. To investigate the behavior of overlapping passive zones and its impact on the passive soil resistance capacity are the main purpose of this study. In the finite element analysis, the Plaxis programme is preferred by the authors. The author is also carried out the sensitivity analyses with respect to prescribed displacement, interface geometry, soil/wall friction, mesh refinement, boundary conditions, unloading–reloading Poisson’s ratio and soil stiffness. At the end of their study, the authors point out that the developed model can be used as reference for reproducing the results for homogeneous soil layering in fully drained conditions. Sadoglu [37] examined the design optimization of symmetrical gravity retaining walls. The design of the wall was carried according to the Building Code Requirements for Structural Concrete (ACI 318-99). To reduce the costs of the total wall, the cross-sections area of the wall is selected as an objective function by the author. The problem is solved by developing computer program-based interior point method. The constraint of this optimization problem are design constraints, bending verification constraints, bearing capacity constraint, shear verification constraints, total vertical forces within the middle third of the base constraint, sliding constraint and the overturning constraint. Khajehzadeh et al. [38] presented a study on the economic design of retaining wall using particle swarm optimization with passive congregation. The authors developed a computer program in MATLAB using PSOPC (particle swarm optimization with passive congregation which was proposed originally by He et al. [39]). This program is only required to feed the input parameters like soil and material properties and safety factors. They used the cost of the retaining wall as an objective function and taken into account the penalty function method to applying the constraints which are the geotechnical and structural design limits. The cost of the total wall consists of the unit price of concrete, excavation, backfill, formwork, and reinforcement. Das et al. [40] used the elitist non-dominated sorting genetic algorithm (NSGA-II) for the optimum design of retaining wall. They considered both cost and the factor of safety at the same time in the optimization process of the wall and carried out the multi-objective optimization approach. So, they obtained of effective Pareto optimal solutions instead of a single solution. The structural stability is the constraint of the optimization process for this study. The authors obtained both suitable FOS and the corresponding cost the corresponding footing dimensions and percentage of reinforcement.
Tonne & Mohite [41] optimized the counterfort retaining wall with relief shelf. In generally, height of 6 m is suitable and economic for the cantilever retaining wall. But it becomes uneconomical above this height. To support more height of earth mass advancement is done in cantilever retaining wall by adding relief shelf in it. In the view of this idea, the authors realized an optimization process. They point out that counterfort retaining wall of heights 10 m, 12 m, and 15 m with relief shelf at h/2 (h: height of stem) gets minimum earth pressure, minimum overturning moment and better stability. Thus, the cost function of the related problem will be reduced. Singla & Gupta [42] studied on three types of the wall which are cantilever retaining wall, counterfort retaining wall and retaining wall with relieving platforms. They used cost function as an objective function of the optimized problem. The cost function consists of the volume of concrete and the amount of steel. The constraints of the problem are eccentricity, factor of safety against overturning and sliding, the maximum and minimum bearing pressure, maximum and minimum reinforcement percentage, reinforcement spacing and maximum shear stress. The authors concluded that among all the cases the optimal cost required is least in case of retaining wall with relieving platform. Gandomi et al. [43] presented a study by using some resent optimization techniques: These are the accelerated particle swarm optimization (APSO), firefly algorithm (FA), and cuckoo search (CS). The authors aimed to optimize the cantilever retaining wall based on the ACI 318-05 procedure. The design variables are continuous for wall geometry and discrete for steel reinforcement. The overturning, sliding, and bearing capacity failure modes are the geometrical constraint and the shear and moment failure at the stem, heel, toe, and shear key are the structural design constraint of the optimization problem. Sable and Archana [44] used the “optimtool” in MATLAB to find the minimum cost and weight for concrete retaining walls. The overturning, sliding, and bearing stress are the constraint of the problem. The authors categorized to the design variables in two groups: geometric dimensions of wall cross-section and steel reinforcement. Geometric design variables can be continuous or discrete values. But steel reinforcement variables are discrete. Sheikholeslami et al. [45] combined the firefly algorithm (FA) and harmony search (HS) technique (IFA–HS) to solve design problems of reinforced concrete retaining walls. In this new technique, the HS operators are integrated into the FA. The authors used the IFA–HS to optimize the reinforced concrete retaining walls. The costs of concrete and steel reinforcement are taken into account as an objective function. Factor of safety, stability, and material properties of the wall are the constraints of the optimization problem carried out by the authors. At the end of the study, the authors concluded that the IFA–HS algorithm was both computationally efficient and capable of generating least–cost retaining wall designs.
Babu & Basha [46] studied on the optimum design of cantilever retaining walls using target reliability approach. To design the wall the overturning, sliding, eccentricity, bearing, shear and moment capacity of toe slab, heel slab, and stem are taken into account the limit parameters of the problem. In this study, the authors gave detailed information about the structural analysis of the retaining wall. The authors of this paper stated that if the backfill material is well engineered and if the coefficient of variation is less, then a considerable amount of savings in concrete can be achieved. Babu and Basha [47] presented another study on the optimum design of cantilever sheet pile walls in sandy soils using inverse reliability approach. Al-Shukur & Al-Rammahi [48] presented a study on the optimum design of semi-gravity retaining wall subjected to static and seismic loads. They used the ANSYS to realize the finite element modeling of the wall‒backfill‒foundation interaction model. The objective function of the problem is the minimization of the crosssectional area of the retaining wall. The geometric properties of the wall are selected as design variables. The authors compared the results obtained by using zero-order optimization method in ANSYS with the results obtained by using the optimization techniques GA, PSO, and CSS. Deb & Dhar [49] used multi-objective optimization technique to design stone column-improved soft soil. The Non- Dominated Sorting Genetic Algorithm II (NSGA-II) is carried out by the authors. NSGA-II was firstly proposed by the Deb [50]. The authors presented two models named as OMF-I and OMF-II. In OMF-I, there were two objectives; the minimization of maximum settlement over space and the minimization of differential settlement over space. In OMF-II, the objective function is the same with the OMF-II, but there is an additional objective function which is maximization of the average degree of consolidation. Jasim & Al-Yaqoobi [51] made a study on Optimum Design of Tied Back Retaining Wall. The authors used the GA in the optimtool of Matlab to design the wall. The design variables of this study are the geometric dimensions and the amounts of reinforcement. The bending moment and shear force capacities, and some of the other measures are taken into account the constraint of the problem. At the end of the study, the authors concluded that the increase of the allowable stress of tie steel leads to the decrease of the minimum cost.
Optimization in transportation Problems
Transportation becomes possible the communication between and within towns, cities or communities to develop of the civilization. It deals with the planning, designing, constructing, operating of the road, highway, railway, traffic, infrastructures and so on. Sustainability concept considering economic, social and environmental factors together has been also recently implemented in this area. Optimization defined as finding of the optimal solution satisfying some criterion has been also carried out in the transportation. In this subsection, it is presented some research papers which were studied in this engineering field. Putha et al. [52] applied ACO algorithm to solve the oversaturated network traffic signal coordination problem. They identified timing strategies of two example network using the proposed algorithm. One of two models networks examined in [52] was taken from the technical literature while other was an actual traffic network model of the City of Fort Worth traffic signal network. And the obtained results were compared with the previous studies which were employed GA to solve the oversaturated signal coordination problem. Finally, it was concluded that for the higher number of model executions, ACO become a good alternative to solve the problem of signal coordination for oversaturated traffic networks. Marti et al. [53] described a procedure to obtain the economic cost of pre-stressed concrete precast road bridges. Their algorithm employed a variant of SA as a solver. Optimization problem of double U-shaped crosssection and isosatic spans bridges was described with 59 discrete design variables including the geometry of the beam and the slab, materials in the two elements, as well as active and passive reinforcement. Depending on the results obtained in [53], it was expressed that different economic scenarios for steel and concrete costs affect the properties of the cost-optimized bridges. Carbonell et al. [54] handled cost minimization problem of reinforced concrete vaults in road construction. Three heuristic optimization methods were implemented to conduct optimization process. One of three methods is SA. For the optimization problem, the cost of the vaults was taken as objective function while 49 discrete design variables were considered. Applying the three optimization algorithms, 10% cost saving was obtained for the vault of 12.40 m of horizontal free span, 3.00 m of vertical height of the lateral walls and 1.00 m of earth cover with respect to its traditional design. Among the applied optimization algorithms, SA outperformed over others in terms of best results.
Martinez et al. [55] described a methodology to determine the most economical tall bridge piers used in deep valley bridge viaducts. For the economical design, three different types of rectangular hollow tall piers were examined for road piers of 90.0m in height. To solve the combinatorial problem, a variant of ACO was carried out. Numerical results obtained by implementing ACO algorithm indicated that the unit price of the internal formwork influenced by the cost of piers, and a type of pier denoted as RTRA90 was found the most economic pier satisfying the design constraints. Garcia-Segura et al. [56] considered the effects of the cost, the safety, and the corrosion initiation time together to optimally design post-tensioned concrete box-girder road bridges. The cross-section geometry, the concrete grade, and the reinforcing and post-tensioning steel of the deck were adopted as design variables. To decrease the computational effort taking more time for the finite-element analysis of the bridge and also to attain an increment of evaluating the conflicting objectives an integrated multi objective HS with artificial neural networks was proposed. The proposed methodology offers trade-off solutions that satisfy comparatively each need for the decision maker. Stevanovic et al. [57] addressed the importance of reducing excessive fuel consumption and vehicular emission on urban streets. To handle this problem traditionally signal timing is optimized. They proposed a tool based on integrating of three previously developed tools called as VISSIM, CMEM, and VISGAOST to optimize signal timings and minimizing fuel consumption and CO2 emission. A 14-intersection network in Park City, Utah was considered as a case study and two major objectives; i) comparison of estimated of the fuel consumption, and ii) minimize vehicular emissions were taken into consideration for the VISGAOST optimization of signal timing. Numerical results demonstrated that the commonly used formula to estimate fuel consumption has not produced a reliable objective function value for the signal timing optimization. Lhee et al. [58] proposed a new approach to predict the owner’s cost contingency, which has a significant impact on project financial success and other organizational activities critical, on transportation construction projects. To accomplish this, aim an optimization algorithm based on PSO was used. Evaluation of the PSO-based prediction model was tested on data collected from 492 Florida Department of Transportation projects completed from 2004 to 2006. Its performance was compared with an existing ANN-based approach. The PSO-based prediction model developed in this study has potential for forecasting problems such as estimating cost contingency.
Sabatino et al. [59] proposed a framework to eliminate the effect of structural failure of highway bridges on the economy, society, and the environment. Sustainability and maintenance in the optimization model were treated to provide decision-support framework to decision makers in order to balance conflicting objectives. GA based optimization procedure was used to reach the optimal solution in terms of maintenance interventions. The validity of the proposed approach was tested on an existing highway bridge located in Colorado. The framework is able to aid decision making concerning maintenance actions of highway bridges. Barone et al. [60] addressed deterioration process resulting from multiple mechanical and environmental conditions for civil infrastructures and indicated the proposal of life-cycle optimization techniques supply a rational approach to manage these structure systems. To this end, they developed a novel optimization procedure for lifecycle inspection and maintenance planning of aging structures. Bi-objective optimization procedure defining as minimization the maximum expected annual system failure and expected total cost of inspection and maintenance plans solved by means of GA. Findings obtained demonstrated that the proposed approach is efficient for the optimal life-cycle maintenance scheduling of deteriorating systems. Cai and Aref [61] stated some technical cumbersome resulting from increasing span of cable-stayed bridge and using traditional materials have not produced satisfactorily results to relieve these technical challenges. They developed a GA-based optimization procedure to cope with this problem. The proposed procedure was able to find the optimal distribution of fiber reinforced polymeric composites for the deck and cable system of cable-stayed bridges. Numerical experiments shown that optimal combination of hybrid glass FRP-concrete deck and carbon FRPsteel cable systems offers 33 and 12% performance improvement on the static and aerodynamic behavior of cable-stayed bridges. Cai and Aref [62] addressed usage of carbon fiber reinforced polymeric (CFRP) materials as an alternative to the traditional materials for long-span cable-stayed bridges. As in [61], they also implemented a GA-based optimization procedure to find optimal combination of CFRP composites with steel. Unlike [61] which were carried out a multi-objective optimization, single objective being maximization of the critical flutter velocity was adopted in [62] for the optimization process. It was concluded that optimal combination of CFRP and steel caused to maximize the flutter performance of cable-stayed bridges. Chen et al. [63] applied IPSO and GA-based algorithm to determine the form-finding analysis of a suspension bridge installation. A form-finding analysis for the main span of the Yingwuzhou Yangtze River Bridge was conducted employing the stated optimization algorithms, and the proposed a novel IPSO-based form-finding method for suspension bridge design and construction overcomes shortcomings of the conventional formfinding methods.
Silva et al. [64] addressed the importance of the environmental and operational effects on the structures, which result in some deterioration of structures. They proposed a novel damage detection method based on unsupervised and nonparametric GA to specify the damage in bridges arising from the presence of environmental and operational influences. The GA was also strengthened by a novel concentric hyper sphere algorithm. The capabilities of the method were investigated on the structural damage detection process of two ridges: Z-24 Bridge and Tamar Bridge. Findings showed the robustness and effectiveness of the proposed approach on detecting the damage on bridge system. Liu & Chang [65] presented a GA-based solution procedure to optimize an arterial signal problem. According to the traffic patterns obtained from the end of the optimization procedure, one of two alternatives indicating as either minimizing the total travel time or maximizing the total throughput over the target area for the control objective can be chosen. Experimental analyses carried out an example arterial of four intersections by using the GA-based solution approach demonstrated the effectiveness of it in design of arterial signals, especially under congested, high demand traffic conditions. Hu & Liu [66] proposed offset optimization model based on GA and objective of which was to minimize total delay for the main coordinated direction and to consider the performance of the opposite direction at the same time. The proposed methodology was examined on a main arterial (TH55) in Minessota, and it was able to achieve decreasing the travel delay of coordinated direction significantly without compromising the performance of the opposite approach. Sharma & Kumari [67] conducted a literature survey regarding the utilization of the ACO, BFO, and PSO algorithms in traffic route optimization. ACO was employed in generally traffic controlling and reducing vehicle collisions, optimization of a rail vehicle floor sandwich panel, and vehicle routing design. On the other hands, as comparing the other techniques PSO was able to decrease the computational complexity, and to increase the convergence of the traffic path and more complex path choice models.
Xiao et al. [68] investigated the optimal adjustments of gradation, method of composite modification, and compaction checking in order to enhance the high-temperature performance of the asphalt–rubber mixture. Through these optimal adjustments, they reached improvement considerably on the dynamic stability and relative deformation indices of the asphalt–rubber mixture. The numerical examples demonstrated that the optimal adjustment was for 12 round-trip for the rolling time and 180-190 °C for the compaction temperature of the asphalt-rubber mixture. Ghanizadeh [69] developed an optimization model to specify the optimal combination and thickness of different pavement layers that is one of the costly parts of transportation infrastructures. The implementations obtained from the use of proposed optimization model address that application of asphalt treated layer in pavement structure was not cost effective, and also with increasing the strength of subgrade soil, the subbase layer might be taken out from the optimum structure of pavement. Santos & Ferreira [70] programmed an optimization model allowing pavement performance for Life Cycle Cost Analysis (LCCA) to offer the best pavement structure for a road or highway for the designers. OPTIPAV developed tool for this aim was utilized for obtaining LCCA solution of flexible pavements under the serviceability conditions adopted in AASHTO. The applications of the new system indicated that it is satisfactorily alternative tool for the road engineer’s toolbox.
Optimization in construction managements problems
Construction engineering and management as field of engineering might be summarily defined as planning projects, estimating and controlling costs, administering contracts, organizing construction sites, managing construction process, optimizing site activities. In order to respond to this need, the professionals use advanced management techniques. Generally speaking, it might be stated for this engineering field that optimization models were developed and applied to determine the optimal adjustment of time, cost, quality, environment, safety, and so on. Some of these implementations are addressed in this subsection as follow. Koo et al. [71] expressed difficulty of making decision under the diverse conditions, like time, cost, quality, etc. in case of the construction projects getting larger. They developed an integrated Multi-Objective Optimization (iMOO) model employing GA as an optimization algorithm. The robustness and reliability of the proposed model were evaluated on the construction timecost trade-off problem. The model is capable of handling of more than two objectives and using four types of fitness evaluation functions. It might be applied in other areas, i.e. energy use. Azeez & Alsaffar [72] utilized ACO algorithm as an optimizer for the timecost optimization problem encountered in the field of construction project management in order to obtain a balance between two complex objectives (cost and time). The created model applied on a construction project including 7 activities which contains 4860 possible solutions. By means of optimization process, they obtained 54.4% and 15% reduction on time and cost, respectively for the tested example. Aziz et al. [73] suggested a model to the construction planners to find an optimal adjustment to resource allocation in order to minimize project duration and its cost. The model is also capable of taking for the maximization of quality. It integrates the features of CPM and GA to optimize the construction total time, total cost, and total quality. Model validation was examined on a case study including 18 construction activities, and the created model enables satisfactorily decrease in three main tasks (time, cost and quality) considered simultaneously for a construction project. Narayanan & Suribabu [74] used DE algorithm to reach a solution among the challenging alternatives of time, cost and quality for construction project. The suggested approach was implemented for two multi-objective time-cost-quality problems. First one consists of seven while other 18 construction activities. Comparing with existing ones, the presented approach was able to generate best optimal solution for construction multi-objective optimization problems that minimize time and cost of the projects while maximizing quality
Zhang & Li [75] emphasized significance tradeoff between time and cost mutually linked for a construction project. They developed a PSO-based multi-objective optimization to determine an optimal set of activity methods with the objectives of minimizing project duration and total cost. To verify the performance of the proposed model two examples previously introduced were adopted. Solution of these 7 and 18 activities demonstrated that the developed model provides an alternative solving methodology for time-cost tradeoff problem. Elbeltagi et al. [76] aimed to optimize a project scheduling problem including all design criteria such as time, cost, resource, and cash flow. For this purpose, they developed a multiobjectives overall optimization model based on PSO for project scheduling problem. The model was corrected on project divided in to 24 major activities. Numerical experiments carried out for a real-life case study construction example demonstrated that multi-objectvie PSO technique was able to produce results each of all offers satisfactory alternative solution for multi-objective optimization of construction projects. Bettemir & Birgönül [77] discussed advantage and disadvantages of heuristic, meta-heuristic algorithms and exact method used for solving time-cost trade-off problem. They proposed a network analysis algorithm based on minimum cost-slope concept to optimize discrete time-cost tradeoff problem. The network analysis algorithm was examined on 18 and 63 activity projects, and it was concluded that computational demand of the proposed approach to find the optimum or nearoptimum solution is significantly lower than the meta-heuristic algorithms. Afshar et al. [78] introduced a new multi-colony ACO algorithm to tackle the time-cost trade-off problems. They embedded an innovative solution exchange strategy in their model in order to suggest more alternative solutions concerning in timecost trade-off problems for the decision makers. The proposed algorithm was tested on an 18-activity time-cost problem, and it outperformed over the weighted approach to determine the nondominated solutions in a combinatorial optimization problem. Aminbakhsh & Sonmez [79,80] developed a novel PSO-based multi-objective optimization environment enhanced with some novel principles such as particle representation, position-updating to solve the discrete time-cost trade-off problem for medium and large-scale construction projects. Some computational experiments were conducted on different construction projects varying from 18 to 630 activities, and the results shown that the new method outperforms the state-of-the-art methods, both in terms of the solution quality and computation time. Sonmez & Bettemir [81] introduced a hybrid strategy combined useful features of GA, SA, and QSA for the discrete time-cost trade-off problem. Hybridization scheme takes advantage of SA for enhancing hill-climbing ability of GA, while QSA is used to improve local search capability. The hybrid algorithm was proved on test problems with a range of 18 to 630 activities. Based on the numerical results, it might be expressed that the hybrid strategy is a good option to be employed for the solution of discrete time-cost trade-off problem.
Zhang & Ng [82,83] developed an ACO based decision support system to solve the Multiobjective time-cost optimization problems. They linked ACO algorithm to Microsoft Project via Visual Basic for Application, and a test project consisting of 18 activities was investigated to demonstrate the performance of the proposed model. ACO-based model finds better solution for the test study with less computational effort. Geem [84] utilized a HS algorithm to carry out bi-objective optimization problems, which take into account the relationship between time and cost being correlated. HS algorithm was applied two networks of up to 18-activities, and effectiveness of Pareto solutions obtained using HS were compared with those found by GA and ACO. Although the test cases were small scale projects, the implementation proposed model was anticipated that it can be used to solve the large-scale networks. Magalhaes-Mendes [85] proposed a hybrid GA to solve optimization problem including time, cost, and quality simultaneously as objectives. The robustness of the proposed model was tested on a small-scale test project consisting of 7-acticvity and compared with ACO and DE algorithms developed in advance to solve multi-objective optimization problems. The presented approach provided alternative for the solution of construction multi-objective optimization problems. Rostami et al. [86] stated that solution methods proposed for project scheduling problem lose their efficiencies as the dimension of the problem is getting bigger. They developed two algorithms, one of which is an enhanced GA, to tackle this mentioned loss of efficiency. The proposed models were employed in the solution of projects with 30, 60, 90 and 120 activities. Computational results indicated that the improved GA was capable of solving the majority of the problems investigated in their study with less error than other metaheuristic methods. Monghasemi et al. [87] applied an evidential reasoning approach for the first time in the field of project scheduling to determine the best solutions in the Pareto set for discrete time-cost-quality trade-off problems. The proposed model realized on a highway construction project and it shown efficiency in examining the performance of each scheduling option according to multiple time, cost, and quality criteria.
Choddousi et al. [88] addressed intercompabilities of the cost and duration of the activities and allocated resources and resource leveling. Therefore, they together adopted the problems known as resource-constrained project scheduling problem, discrete time–cost trade-off problem, and resource allocation and resource leveling problem in their optimization model. Application of the model demonstrated that model provides more practical solutions in terms of resource allocation and leveling. Tavana et al. [89] proposed a new multi-objective multi-mode model for solving discrete time-cost-quality trade-off problems with preemption and generalized precedence relations. Adding of preemption and generalized precedence relations in project scheduling problems made the problem investigated more appropriate with real-life projects. Zamarrón-Mieza et al. [90] recently reviewed the application of multi-criteria decision analysis for aging-dam management. Multi-Attribute Decision Making techniques had a major presence under the single approach, especially the Analytic Hierarchy Process, and its combination with Technique for Order of Preference by Similarity to Ideal Solution was prominent under the hybrid approach; while a high variety of complementary techniques was identified. A growing hybridization and fuzzification are the two most relevant trends observed. The integration of stakeholders within the decision-making process and the inclusion of trade-offs and interactions between components within the evaluation model must receive a deeper exploration. Despite the progressive consolidation of Multi-Criteria Decision Making in dam management, further research is required to differentiate between rational and intuitive decision processes. Additionally, the need to address benefits, opportunities, costs and risks related to repair, upgrading or removal measures in aging dams suggests the Analytic Network Process, not yet explored under this approach, as an interesting path worth investigating. Penadés-Plà et al. [91] examines 77 journal articles of multi-criteria decision-making methods at each life-cycle phase of a bridge, from design to recycling or demolition. This investigation showed the use of different methods in the decision-making phases of sustainable bridges. In addition, the differences between multi-attribute and multiobjective decision-making were explained, showing examples of multi-objective decision-making. The criteria and methods applied to each life-cycle phase, as described by the authors, are indicated. Finally, a statistical study was carried out to show trends between the methods and the life-cycle phases.
Optimization in hydraulic problems
Optimization of drinking water, water distribution system expansion, groundwater pollution source identification, reducing background leakage, estimates of energy consumption, designing water networks, modeling discharge–sediment relationship are the simple application of optimization on the hydraulic problems. The studies presented in recent years using optimization algorithms for hydraulic problems are given below. Bayram et al. [92] studied the viability of teaching–learning based optimization (TLBO) algorithm for the first time in the estimation of the stream dissolved oxygen (DO) concentration. They also compared the validity of TLBO algorithm with those of the artificial bee colony algorithm as well as the conventional regression analysis techniques. It was seen that the TLBO algorithm provided better estimation, with an improvement of nearly 20%. They deduced that the equations derived by using the TLBO algorithms estimate the stream DO concentration successfully. Morleya & Tricaricob [93] compared the population-based optimization techniques for water distribution system expansion and operation. They formulated the problem as single and multiple-objective optimization problems. For the multiple-objective optimization the Non-dominated Sorting–II (NDS-II) approach is preferred. The objectives functions of the problem are the total cost (pipe replacement and duplications, tank, pump and valve installation, and annual operational) and Leakage (the absolute annual volume of water lost as leakage). The authors compared the results obtained by NSGA-II (Non-dominated Sorting Genetic Algorithm) and Omni-Optimizer (OO). A similar study is made by Arandia et al. [94]. Irani & Nasimi [95] presented a study on the application of artificial bee colony-based neural network in bottom hole pressure prediction in underbalanced drilling. To improve the efficiency and prediction capability of artificial neural network the artificial bee colony is integrated to the ANN by the authors. The performance of the model proposed by the authors was evaluated using mean square error (MSE) and efficiency coefficient R2. When the authors compared the measured and predicted value for bottom hole circulating pressure (BHCP), a good agreement was obtained. A similar study using ANN with ABC is made by Kisi et al. [96]. They investigated the accuracy of artificial neural networks (ANN) with artificial bee colony (ABC) algorithm for modeling discharge-suspended sediment relationship.
Uzlu et al. [97] applied the ANN (artificial neural network) model with the teaching-learning-based optimization algorithm to estimate energy consumption in Turkey. The TLBO algorithm was first time applied such a study by the authors. The energy consumption of Turkey until 2020 was obtained by the ANN-TLBO model. The authors concluded that the future energy consumption of Turkey would vary between 142.65 and 158.00 Mtoe in 2020. Karbasi [98] investigated the applicability of TLBO algorithm for the modeling hydraulic jump length over a smooth horizontal bed. The author used linear, quadratic, power and exponential regression forms in the TLBO. The hydraulic jump data was taken from USBR reports. At the end of the study, the author concluded that the TLBO based models had good agreements with the measured experimental data. Blinco et al. [99] used the genetic algorithm optimization of operational costs and greenhouse gas emissions for water distribution systems. This study was previously presented in the 16th Conference on Water Distribution System Analysis, in 2014.The main purpose of the study is to minimize the operational greenhouse gas (GHG) emissions. The model prepared by the authors was linked to hydraulic simulation software EPANET and a Microsoft Excel interface. In this study there are more than one objective function such as cost, energy and GHG emissions. Quiniou et al. [100] dealt with optimization of drinking water and sewer hydraulic management. They used the non-dominated sorting genetic algorithm to solve multi-objective optimization problem. The objective functions of the authors’ problem are: “energy cost” and “water purchase and production cost”. The constraint of the problem are: Maximum water purchase capacity – purchase, Time of exceeding of minimum volume of storage in tanks, number of tanks without conservation of level on 24 hours and number of pumps over maximum frequency of starting/stopping pumps. Peralta et al. [101] made a study on the multi-objective genetic algorithm conjunctive use optimization for production, cost, and energy with dynamic return flow. The main objective functions used this study are: maximizing water provided from sources, maximizing hydropower production, and minimizing operation costs of transporting water from sources to destinations. The authors used the non-dominated sorting approach to find Pareto optimal solutions set for the multi-objective optimization problem and used substitute simulators during optimization to reduce computational effort.
Fayad et al. [102] presented a simulation/optimization (SO) model doing that via artificial neural network simulators and genetic algorithm optimizer for multi-objective conjunctive water use problems. The design variables of the optimization problem are spatially distributed groundwater pumping, reservoir diversion, stream diversion, and reservoir release rates. The upper and the lower bound of the design’s variables are taken into account as constraint of the optimization problem. There were two objective functions. The first one is the maximization of average water provided from pumping wells, stream diversions, and reservoir diversion. The second objective function is the maximization of hydropower production by maximizing reservoir releases thru the turbine. Bahrami et al. [103] used the simulated annealing and genetic algorithm to solve groundwater inflow problem to an advancing open pit mine. The authors developed a hybrid model by using artificial neural network (ANN) with the GA and SA. The authors used the MATLAB software to carry out their purpose and used the SEEP/W package to verify the accuracy of these hybrid models. At the end of their study, the authors concluded that the ANN–GA, ANN–SA and numerical models results all have a good fit with the field data, but the ANN–GA model shows the best correlation. Luo et al. [104] presented a study by using the harmony search for the optimal design of groundwater remediation system. They developed a new probabilistic multi-objective fast harmony search algorithm (PMOFHS). The objective functions of the study are: minimization of the total remediation cost through the engineering planning horizon, and minimization of the mass remaining in the aquifer at the end of the operational period. The authors also used the Monte Carlo (MC) analysis to evaluate the effectiveness of the proposed methodology. Yang et al. [105] examined the tabu search algorithm for the multi-objective optimal design of groundwater remediation systems. They developed a new multi-objective optimization method called the niched Pareto tabu search (NPTS). The objective functions of the problem are the minimizations of both remediation cost and contaminant mass remaining in the aquifer. The authors concluded that for a separate optimization model run, compared with the NSGA-II, the NPT S reduces the runtime by 21.5%. Yaseen et al. [106] used the firefly algorithm with the Adaptive Neuro-Fuzzy Inference Systems (ANFIS) for stream flow forecasting. The authors used the historical monthly stream flow data for Pahang River. The results of this study also show that the ANFIS-FFA is not only superior to the ANFIS model but also exhibits a parsimonious modeling framework for stream flow forecasting.
Optimization in structural problems
Structural optimization can be classified into three classes of problems, although some problems usually fall into more than one. The first is the dimensional optimization with consider as design variables the sizing of the elements, which can vary continuously or can be taken from a list of available cross-sectional dimensions (or profiles). The second is the geometric optimization, considering the nodal coordinates as variables. Finally, the number of elements characterizes the topology optimization. In general, minimization of cost or weight is the objectives to be achieved, and the constraints are related to design codes and requirements. Probably the first computer application of structural optimization was a study developed by Schmit in 1960 related to minimum weight of a three-node plane truss. From then, a big diversity of applications has been studied, such as trusses, grillages, beams, frames, building floors, bridges, transmission towers and guyed masts. Some of these recent applications are presented in the sequence. Jalili & Hosseinzadeh [107] used Culture Algorithm to obtain minimum weight of trusses under stress and deflection constraints. Cross sectional area of each member was taken as the design variables. In order to test the performance of the method, four trusses were analyzed. The obtained results showed the efficiency of the method in finding the optimal design, obtaining. When compared to other classical methods, Culture Algorithm conducted to lighter structural weights with less structural analyses. Cicconi et al. [108] studied a methodology to reduce the weight and the cost of big steel structures during the early design phase. A platform-tool was developed to support the automatic optimization of steel frames using genetic algorithms and SAP2000 software. A test case chosen was an oil & gas module of an existing onshore power plant. Two different studies were proposed: the first were focused on weight minimization and regarded only to static loading, while the second considered three loading cases (static, load transport and sea transport). Using the proposed optimization method, the mass was reduced between 5% and 15%. Medeiros & Kripka [109] applied optimization to minimize the cost of reinforced concrete beams in order to propose pre-sizing parameters. The cross-sectional height of each group of beams was taken as design variables. The constraints were related to flexural, shearing, torsion, web reinforcements and serviceability limit states. An optimization software was developed by the association of grillage analysis and simulated annealing optimization method. The influence of relative cost of steel, concrete and formwork on total cost was also investigated. According to authors, simulated annealing heuristic was efficient in minimizing structure costs, and the software can be an important tool for the pre-sizing of building floor grids and also for individual beams. Kaveh & Talatahari [110] combined a variant of Particle Swarm with Ant Colony and Harmony Search methods into a new method named discrete heuristic particle swarm ant colony optimization (DHPSACO). This method was then employed to discrete optimization of trusses. Four structures are tested to in order to verify the efficiency of the proposed method. According to authors, better solutions were obtained compared to other classical algorithms. These solutions were obtained with less computational time and high speed of convergence.
Souza et al [111] optimized transmission line towers, being the structure divided in modules, which can assume different pre established topologies. Simultaneously to topology, also shape and size were optimized. Two numerical examples were assessed, being the first a tower with eight different load cases and the second a self-supported tower subjected to a scenario of cable rupture and a wind load hypothesis. The obtained results indicated a reduction of up to 6.4% of the structural weight, when compared to a classical procedure of size optimization. Dede & Ayvaz [112] studied the optimization of plane and space trusses with a Teaching-learningbased optimization (TLBO). Cross-sectional areas of bars and nodal coordinates were considered as the design variables. The method was applied to five structures. When compared to results obtained by other studies, it was concluded by the authors that the algorithm can be effectively used to design truss structures. Pholdee & Bureerat [113] compared the performance of 24 metaheuristic methods for truss optimization with dynamic constraints. Established methods were used to minimize mass of five different trusses. Based on a statistic analysis, the authors concluded that the best performance optimizers were evolution strategy with covariance matrix adaptation and differential evolution. Alapati [114] used genetic algorithm (GA) to weight minimization of plane trusses. The stresses and deflections were considered as the constraints of the problem. The method was applied to a classical benchmark structure (ten-bar truss). Some conclusions regarding GA parameters were presented. Chowdhury et al. [115] modeled plain concrete and steel fiber reinforced concrete (SFRC) cylinder specimens numerically, with experimental validation. The experimental study evaluated the increase in capacity of cylinders of stone and brick concrete and SFRC. The numerical study aimed to optimize the main controlling parameters to model concrete and SFRC in finite element platform. The final results presented a good correlation among numerical and experimental results. Farshchin et al. [116] introduced a multi-class teaching–learning-based optimization technique (MC-TLBO) to structures optimization with frequency constraints. The algorithm was tested with several truss structures, and the results were compared to those obtained with a modified TLBO algorithm and with other methods. The results indicated that the method can lead to low cost designs. In addition, a statistic analysis indicated that MC-TLBO was more robust and efficient than other studied techniques. Talaslioglu [117] minimized weight and joint displacements of grid structures, being the constraints related to serviceability and ultimate strength. Four Multiobjective optimization algorithms were applied to three examples and compared using different combinations of optimizer related parameters. To the examples analyzed, Adapting Scatter Search showed the best performance.
Belevicius et al [118] presented a technique for simultaneous shape, sizing and topology optimization of tall guyed masts. The mast structure was optimized for self-weight and wind loading, considering strength, stability and slenderness constraints. The nonlinear behavior of the guyed mast is simplified idealizing the nonlinear guys as approximate boundary conditions for the mast. The genetic algorithm with preprocessor for genome repair was used as the primary optimization engine. After the best solution from the set of EA solutions is selected, the pattern search algorithm was employed to explore the neighborhood of the solution in depth. Using the proposed technique, a typical 96 m steel guyed mast carrying a standard antenna cluster was optimized. The optimization of the mast with different sets of design parameters showed that the most relevant schemes of the mast have three to five guys’ clusters, with the optimal scheme being the mast with five guys’ clusters. Poitras et al. [119] adopted Particle swarm optimization (PSO) for the minimum mass or cost design of composite and non-composite steel floor systems. The design variables were the size of girders and secondary beams, as well as the stud spacing and the concrete thickness. The performance of the algorithm was tested for three floor configurations. According to authors, PSO algorithm achieved the optimal results to all examples. Dede [120] used Teaching–Learning-Based Optimization algorithm (TLBO) for the minimum weight design of grillage systems. The design variables were the cross-sectional areas of W-shapes, considered as discrete variables. Several structures were optimized aiming to investigate the efficiency of the algorithm. The results were compared with those obtained from previous studies. According to the results, TLBO algorithm outperformed the other algorithms. Kaveh & Bakhshpoori [121] presented the application of the Cuckoo Search (CS) to weight minimization of truss structures, considering both discrete and continuous design variables. In order to investigate the performance of the algorithm, three examples were presented, consisting of two space trusses and a dome-shaped truss. The results, presented in terms of results and number of function evaluations, indicated the robustness of the algorithm. Hasançebi et al [122] compared the performance of seven techniques in optimum design of truss structures. First, a verification of the algorithms used to implement the techniques was carried out using a benchmark problem. Next, the techniques were compared in terms of solution accuracies, convergence rates and reliabilities using four real size design examples formulated according to the design limitations imposed by ASD-AISC. To the examples considered, the results revealed that simulated annealing and evolution strategies presented the best performance. Sharafi et al. [123] presented a procedure for the shape and sizing optimization of open and closed thin-walled steel sections using the graph theory. A multi-objective optimization problem aimed to minimize the mass and maximize the strength of the section. The problems were solved by the usage of multi-colony ant algorithms, and the Pareto-optimal set was obtained. The results showed the applicability of the proposed procedure to shape optimizations of steel sections and sizing optimization roof sheeting.
Fabeane et al. [124] studied the optimization of composite bridges, aiming to reduce the cost of bridge cross section by varying the dimensions of the steel girders. The specification used in the analysis and design of the girders was the AASHTO, and the cases studied were simple span bridges with different spans and a variable number of steel girders. The results obtained enabled the identification of parameters to optimize design of composite bridges, showing that the use of criteria based on optimization techniques can lead to a significant reduction in the cost of the structures. Majumdar et al [125] presented a method to detect and quantify structural damages from changes in modal parameters. Computer codes were developed and applied to beam and frame type structural systems. The structures were modeled with Euler- Bernoulli beam element and damage is represented in terms of SRF. The modal parameters were calculated numerically from eigen value analysis. An extended form of ant colony optimization technique called continuous ant colony optimization was used. The effectiveness of the algorithm was studied with cantilever beam model, a 3-bay 4-storey plane frame model, and a five-storey space frame model. The proposed damage detection method was found to be equally successful regardless of the damage location and extent of damage. Torres-Machi et al. [126] optimized the design of highperformance concrete for reinforced concrete beams, using three hybrid optimization strategies: Variable Neighborhood Descent (VND), Reduced Neighborhood Search (RNS) and Basic Variable Neighborhood Search (BVNS). The algorithms were applied to minimum cost and minimum embedded carbon dioxide emissions. The results indicated that the objective function, both to economic and ecological beams, increases parabolically with the span length.
Optimization in mechanical engineering problems
Optimization techniques are used in Mechanical Engineering in all of its important sub-fields, i.e. design of mechanical elements and systems, design of thermal devices and systems, and manufacturing process and systems. The researchers presented several type of mechanical optimization problems. Some of these problems are; optimizing the material costs and electric-thermal performance, optimal design of selected thermal, optimization aspects of four modern machining processes, optimization of the laminated composite plates, optimization for composite plates, stacking sequence optimization, etc. Rao & More [127] explored the use of an improved Jaya algorithm called self-adaptive Jaya algorithm for optimal design of selected thermal devices viz; heat pipe, cooling tower, honeycomb heat sink and thermo-acoustic prime mover. Four different optimization case studies of the selected thermal devices were presented. The researchers had attempted the same design problems in the past using niched pareto genetic algorithm (NPGA), response surface method (RSM), leap-frog optimization program with constraints (LFOPC) algorithm, teaching-learning based optimization (TLBO) algorithm, grenade explosion method (GEM) and multi-objective genetic algorithm (MOGA). The results achieved by using self-adaptive Jaya algorithm were compared with those achieved by using the NPGA, RSM, LFOPC, TLBO, GEM and MOGA algorithms. The self-adaptive Jaya algorithm was proved superior as compared to the other optimization methods in terms of the results, computational effort and function evaluations. Ocłoń et al. [128] presented a modified Jaya algorithm for optimizing the material costs and electric-thermal performance of an Underground Power Cable System (UPCS). A High Voltage (HV) underground cable line with three 400 kV AC cables arranged in flat formation in an exemplary case study was considered. The performance of the modified Jaya algorithm was compared with classical Jaya and PSO algorithms. The modified Jaya algorithm was reported to give lower values of the cost function.
Rao et al. [129] described multi-objective optimization aspects of four modern machining processes namely wire-electro discharge machining process, laser cutting process, electrochemical machining process and focused ion beam micro-milling process. In order to handle multiple objectives simultaneously a new posteriori multi-objective optimization algorithm named as multi-objective Jaya (MO-Jaya) algorithm was proposed which could provide multiple optimal solutions in a single simulation run. The results of MO-Jaya algorithm were compared with the results of GA, NSGA, NSGA-II, BBO, NSTLBO, PSO, SQP and Monte Carlo simulations. The results had shown the better performance of the MO-Jaya algorithm. Apalak et. al [130] presented a study related to the optimization of the laminated composite plates. They aimed to find maximum basic frequency for composite plates using genetic algorithm (GA). The finite element technique is used in the calculation of the fundamental frequency of the composite plates. The toolbox of the MATLAB programming was preferred by the authors to find maximum first frequency value of the laminated composite plates. The authors used the artificial neural network to reduce the time consuming which is necessary to handle finite element technique to calculate frequency of the model. That is, the neural network model is used as an alternative numerical analysis for calculation of the frequency. Koide et al. [131] optimized the laminated composite plate using ant colony algorithm (ACO). To demonstrate the efficiency of their program, the authors tested the developed algorithm on the four numerical examples. The design variables used in this study are the orientation of the fiber and he material. Cost of the material is selected as an objective function for the developed algorithm. Maximum weight of the structure and the buckling are the limitations of the optimization problem. The developed program based on the ACO showed an excellent performance. In the numerical example, the authors taken into account different type of mechanical problem. As many researchers, the authors used the MATLAB to develop their algorithm. Honda et al. [132] performed a discrete optimization for composite plates. The natural frequencies of the composite layers are the objective function of the optimization algorithm. They defined the best solution of the lamination specifications using gradient technique. In contrast to previous researchers using the genetic algorithm, the authors of this paper developed a simple process. By using different boundary in numerical examples, the correct optimal solutions can be obtained with this developed algorithm. Topal et al. [133] made a study on the stacking sequence optimization by using Teaching– Learning-Based Optimization algorithm. The authors also used the other optimization algorithms technique named Artifical Bee Colony (ABC). In the optimization process the maximum number of iteration and the population size are 100 and 30, respectively. The fiber angle of each layer are the design variables of the area bales of the proposed algorithms. The fundamental frequency of the laminated layer is the objective function of the program. The constraints are not taken into account, that is, this problem can be categorized as an unconstrained optimization problem.
Thamaraikannanand & Thirunavukkarasu [134] used the Teaching-Learning Based Optimization Algorithm (TLBO) for the mechanical optimization problems. They developed a new operator named “Differential Operator” to TLBO by the hope to find better solution than the traditional TLBO algorithm. They also made a statistical study using the maximum, minimum, average and mean value of the objective function to show the performance of the developed program. The objective functions of this developed program are minimum weight and the minimum volume for the related mechanical problem. Yusup et al. [140] addressed that cutting speed, depth of cut and radial rake angle are commonly adopted parameters as design variables in the optimization of machining process. They also stated that to solve this kind of optimization problem generally metaheuristic algorithms were utilized. They reviewed the application of Particle Swarm Optimization (PSO) on those problems related to the machining process, which were studied by the researchers from 2007 to 2011. Based on the review process, they argued that the optimization of machining process handled with PSO is usually associated with the multi-pass turning. On the other hand, they also expressed that the machining performance mostly adopted are the production costs. Apalak et al. [141] applied Artificial Bee Colony (ABC) algorithm as an optimizer in layer optimization of symmetrical laminated composite plates. The problem was examined under different boundary condition schemes, and the main purpose of this optimization process was to maximize the first natural frequency of the corresponding plates system. To fulfill this task the finite element method was employed to identify the first natural frequency of the laminated composite plates under varying stacking sequences. For the investigated problem, the results obtained by using ABC algorithm for the optimal stacking sequences indicated that those were also meaningful when comparing with the results obtained by implementing the genetic algorithm integrated with the finite element method. Karaya & Soykasap [142] highlighted some remarkable features of the composites and why the users utilize these materials in the design of distinct structures such as aircraft, spacecraft, marine vessels etc. They proposed a hybridization scheme to enhance the material properties of the composites. Two hybridization scheme, carbon/ epoxy and glass/epoxy hybrid plies, were exerted. The effect of these hybrid laminate on the cost of composite plates were investigated by employing two different metaheuristic optimization algorithms, GA and SA. Thanks to numerical investigations, they stated that both optimization algorithms implemented were capable of finding the optimal stacking sequences of hybrid composite plates subject to maximization of natural frequencies and buckling load. However, it was also outlined that the overall performance of GA was better than SA.
Sadr & Bargh [143] proposed two enhancements to improve the optimization process conducted to maximize the fundamental frequency of the symmetrically laminated plates. First one was made on the optimization algorithm, GA, through the elitist strategy while the latter was for the calculation of the objective function taken as the natural frequencies with the help of finite strip method. Taking the number of layers, the fiber orientation angles, edge conditions and plate length/width ratios as the design variables, the proposed optimization model was performed for laminated composite plates which have 0.01 length/width ratio and AS/3501 graphite/epoxy material. Consequently, based on the numerical experiments, they argued that the proposed model was able to produce better the results than that reported previously. Le-Anh et al. [144] performed two different optimization processes for the static and dynamic problems of folded laminated composite plates. In the former process, the aim was to decrease the strain energy while in the later one; the maximization of fundamental frequency was taken into account as objective. In both processes, discrete integer values varying from -90 to 90 were adopted as design variables for the fiber orientations. Search processes of the optimal solutions were utilized by the adjusted Differential Evolution (aDE) algorithm. It was a variant of classic DE strengthening with a new mutation operator and ability of handling discrete variables. Besides, corresponding processes also included a newly developed plate element called smoothed triangular plate element in order to simulate effectively the static and free vibration behaviors of folded laminated composite plates. The numerical results obtained by employing the proposed model demonstrated that aDE was capable of improving the rigidity of composite plate by determining the optimal number of layers and arrangement of them properly. Vosoughi & Nikoo [145] developed a Multiobjective optimization model based on the integration of differential quadrature method (DQM), NSGA-II, and Young bargaining model for simultaneous optimization of laminated composite plates. Both the fundamental frequency and thermal buckling temperature for those were tried to maximize in terms of the fiber’s orientations. Using the proposed hybrid method, optimal fibers orientations for laminated composite plates were determined under the varying conditions including boundary, thickness-to-length and aspect ratios.
Nourbakhsh et al. [146] studied multiobjective optimization of centrifugal pumps, which are widely used in process industries to lift fluid from one level to another. In the design of this class of pumps, it was tried to find a solution which satisfies two conflicting objectives; maximization of efficiency (η) and minimization of the required net positive suction head (NPSHr) in a set of centrifugal pumps. They modelled this design problem using group method of data handling (GMDH) type neural networks to map inputs and outputs. They also used a multi-objective particle swarm optimization method to obtain the optimal solutions for the optimization of centrifugal pumps considering two conflicting objectives, η and NPSHr. They concluded that thanks to Paretobased multi-objective optimization it could be outlined some useful optimal design alternatives to be able to improve the performance of centrifugal pumps. Rao & Waghmare [147] optimized the structure of a robot gripper finding the dimensions of elements of the gripper by satisfying the geometric and force constraints. To fulfill this purpose, five different objectives were considered to determine the optimal geometrical properties of robot gripper. To satisfy balances between these conflicted objective seven design variables associated with the geometrical dimension of gripper were taken. Teaching learning-based optimization (TLBO) algorithm based multiobjective model was developed to search the optimal solution. The numerical results obtained from the optimization process indicated that the performance of TLBO algorithm for the multiobjective design optimization of robot grippers was able to compete with those obtained by employing different multi-objective models like MOGA, NSGA-II, and MODE.
Conclusion
The potential and effectiveness of different advanced optimization algorithms are presented in this paper by reporting the works of various researchers in different divisions of civil engineering such as structural engineering, construction management, mechanics, transportation and geotechnical engineering during the last two decades. Approximately 20 optimization algorithms are introduced. The applications of advanced optimization algorithms in mechanical engineering are also presented. It is observed that different optimization algorithms are used for different applications, but one need not claim any particular optimization algorithm as the “best” algorithm among all the optimization algorithms available in the literature. In fact, there may not be any such ‘best’ algorithm existing! A particular algorithm may not be the “best” for all types of optimization problems. If any algorithm is found having certain limitations, then the efforts of the researchers should be to find the ways to overcome the limitations and to further strengthen the algorithm. Researchers are encouraged to make improvements to the existing optimization algorithms and/or to develop new optimization algorithms. Due to the length limitation of the text, other important works were not included in this selection. Anyway, it is remarkable the growing application of optimization to the resolution of real problems. It is concluded that this review paper will be helpful for the researchers related to the optimization technique.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Holland JH (1975) Adaptation in Natural and Artificial System. University of Michigan Press, Ann Arbor, USA.
- Geem ZW, Kim JH, Loganathan GV (2001) A new heuristic optimization algorithm: harmony search. Simulation,76(2): 60–68.
- Karaboga D, Basturk B (2007) A powerful and efficient algorithm for numerical function optimisation: artificial bee colony (ABC) algorithm. J Global Optim, 39: 459-471.
- Glover F (1989) Tabu Search-Part I. ORSA Journal on Computing, 1(3): 190-206.
- Rao RV, Savsani VJ, Vakharia DP (2011) Teaching–learning-based optimisation: a novel method for constrained mechanical design optimisation problems. Comput Aided Des, 43: 303-315.
- Kennedy J, Eberhart R (1995) Particle swarm optimization, Proceedings of the IEEE International Conference on Neural Networks. Perth, Australia, Oceania:1942–1948.
- Erol Osman K, Ibrahim Eksin (2006) New optimization method: Big Bang-Big Crunch. Advances in Engineering Software 37(2): 106-111.
- Kaveh A, Talatahari S (2010) A novel heuristic optimisation method: charged system search. Acta Mech 213: 267-289.
- Yang XS, Deb S (2009) Cuckoo search via levyflights, In: Nature & Biologically Inspired Computing, NaBIC, India:210-214.
- Dorigo M (1992) Optimization, learning and natural algorithms. PhD Thesis, Dept. of Electronics, Politecnico di Milano, Italy, Europe.
- Rao RV (2016) Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. International Journal of Industrial Engineering Computations 7:19-34.
- Yang XS (2010) Firefly Algorithm, Stochastic Test Functions and Design Optimisation. Int. J. Bio-Inspired Computation 2(2): 78–84.
- Kirkpatrick S, Gelatt CD Jr, Vecchi MP (1983) Optimization by simulated annealing. Science 220(4598): 671-680.
- Reynolds RG (1994) An introduction to cultural algorithms evolutionary programming. Proc. 3rd Ann. Conf, World Scientific, River Edge, NJ: 131- 139.
- Storn R, Price K (1997) Differential evolution –a simple and efficient heuristic for global optimisation over continuous spaces. J Global Optim 11: 341-359.
- Kashan AH (2009) League Championship Algorithm: A new algorithm for numerical function optimization. International Conference of Soft Computing and Pattern Recognition:43-48.
- Civicioglu P (2013) Backtracking search optimization algorithm for numerical optimization problems. Applied Mathematics and Computation 219(15): 8121–8144.
- Krishnanand KN, Ghose D (2009) Glowworm swarm optimization for simultaneous capture of multiple local optima of multimodal functions. Swarm Intelligence 3(2): 87-124.
- Geem ZW (2000) Optimalcostdesign of water distribution networks using harmony search. Dissertation, Korea University, South Korea.
- Karaboğa D (2010) Artificial Bee Colony. Scholarpedia 5(3).
- Behera S, Sahoob S, Pati BB (2015) A review on optimization algorithms and application to wind energy integration to grid. Renewable and Sustainable Energy Reviews 48: 214-227.
- Rao RV (2016) Chapter 2, Teaching Learning Based Optimization Algorithm. Springer International Publishing Switzerland: 9-39.
- Shi Y, Eberhart RC (1998) Parameter selection in particle swarm optimization. Evolutionary programming. vol. 1441 of Lecture Note in computers science. Springer, Berlin: 591-600.
- Esmin AAA, Coelho RA, S Matwin (2015) A review on particle swarm optimization algorithm and its variants to clustering high-dimensional data. ArtifIntell Rev, 44: 23-45.
- Lenin K, Reddy BR, Kalavathi MS (2014) A New charged system Search for Solving Optimal Reactive Power Dispatch Problem. International Journal of Computer14(1): 22-40.
- Pholdee N, Bureerat S (2014) Comparative performance of metaheuristic algorithms for mass minimisation of trusses with dynamic constraints. Advances in Engineering Software 75: 1-13.
- Wahab MNA, Meziani SN, A Atyabi (2015) A Comprehensive Review of Swarm Optimization Algorithms. Plos One:1-36.
- Yang XS (2008) Nature-Inspired Metaheuristic Algorithms. Luniver Press, United Kingdom.
- Cheung NJ, Ding XM, Shen HB (2014) AdaptiveFireflyAlgorithm: Parameter Analysis and its Application. Plos One, 9(11): 1-12.
- Bureerat S, Limtragool J (2008) Structural topology optimisation using simulated annealing with multiresolution design variables. Finite Elements in Analysis and Design 44: 738-747.
- Srinivasana S, RamakrishnanS (2012) Multi Objective Optimization of classification rules using Cultural Algorithms. Procedia Engineering 30: 457-465.
- Dogra R, Gupta N (2014) Glowworm Swarm Optimization Technique for Optimal Power Flow. Advance in Electronic and Electric Engineering 4(2): 155-160.
- Yepes V, Alcala J, Perea C, Vidosa FG (2008) A parametric study of optimum earth-retaining walls by simulated annealing. Engineering Structures 30: 821-830.
- Atabay Ş (2009) Cost optimization of three-dimensional beamless reinforced concrete shear-wall systems via genetic algorithm. Expert Systems with Applications 36: 3555-3561.
- Pei Y, Xia Y (2012) Design of Reinforced Cantilever Retaining Walls using Heuristic Optimization Algorithms. Procedia Earth and Planetary Science 5: 32-36.
- Hosseinzadeh S, Joosse JF (2015) Design optimisation of retaining walls in narrow trenches using both analytical and numerical methods. Computers and Geotechnics 69: 338–351.
- Sadoglu E (2014) Design Optimization for Symmetrical Gravity Retaining Walls. Acta Geotechnica Slovenica 2: 71-79.
- Khajehzadeh M, Taha MR, El-Shafie A, Eslami M (2010) Economic Design of Retaining Wall Using Particle Swarm Optimization with Passive Congregation. Australian Journal of Basic and Applied Sciences 4(11): 5500-5507.
- He S, Wu QH, JY Wen, JR Saunders, RC Paton (2004) A particle swarm optimizer with passive congregation. Biosystems 78(1-3): 135-147.
- Das MR, Purohit S, Das SK (2016) Multi-objective Optimization of Reinforced Cement Concrete Retaining Wall. Indian Geotech J 46(4): 354-368.
- VR Tonne, PM Mohite (2015) Optimization and Improvement in Stability of Counterfort Retaining Wall with Relief Shelf. IJRET: International Journal of Research in Engineering and Technology 4(4): 447-451.
- Singla S, Gupta S (2015) Optimization of Reinforced Concrete Retaining Walls of Varying Heights using Relieving Platforms International Journal of Engineering Research & Technology (IJERT) 4(6): 1071-1077.
- Gandomi AH, Kashani AR, Roke DA, Mousavi M (2015) Optimization of retaining wall design using recent swarm intelligence techniques. Engineering Structures 103: 72-84.
- Sable KS, Archana AP (2012) Optimization of Retaining Wall by Using Optimtool in Matlab. International Journal of Engineering Research & Technology (IJERT) 1(6):1-11.
- Sheikholeslami R, Khalili BG, Zahrai SM (2014) Optimum Cost Design of Reinforced Concrete Retaining Walls Using Hybrid Firefly Algorithm. IACSIT International Journal of Engineering and Technology 6(6): 465- 470.
- Babu GLS, Basha BM (2008) Optimum Design of Cantilever Retaining Walls Using Target Reliability Approach. International Journal of Geomechanics 8(4): 240-252.
- Babu GLS, Basha BM (2008) Optimum design of cantilever sheet pile walls in sandy soils using inverse reliability approach. Computers and Geotechnics 35: 134–143.
- Al-Shukur AHK, Al-Rammahi AMA (2017) Optimum Design of Semi- Gravity Retaining Wall Subjected to Static and Seismic Loads. Journal of Civil Engineering and Technology 8(1): 873–881.
- Deb K, Dhar A (2011) Optimum design of stone column-improved soft soil using multi-objective optimization technique. Computers and Geotechnics 38: 50–57.
- Deb K (2001) Multi-objective optimization using evolutionary algorithms. John Wiley & Sons Ltd.
- Jasim NA, Al-Yaqoobi AM (2016) Optimum Design of Tied Back Retaining Wall. Open Journal of Civil Engineering 6: 139-155.
- Putha R, Quadrifoglio L, Zechman E (2012) Comparing Ant Colony Optimization and Genetic Algorithm Approaches for Solving Traffic Signal Coordination under Oversaturation Conditions. Computer-Aided Civil and Infrastructure Engineering 27: 14-28.
- Marti JV, Gonzalez-Vidosa F, Yepes V, Alcala J (2013) Design of prestressed concrete precast road bridges with hybrid simulated annealing. Engineering Structures 48: 342-352.
- Marti JV, Gonzalez-Vidosa F, Yepes V, Alcala J (2013) Design of prestressed concrete precast road bridges with hybrid simulated annealing. Engineering Structures 48: 342-352.
- Martinez FJ, Gonzalez-Vidosa F, Hospitaler A, Alcala J (2011) Design of tall bridge piers by ant colony optimization. Engineering Structures 33(8): 2320-2329.
- Garcia-Segura T, Yepes V, Dan M Frangopol (2017) Multi-objective design of post-tensioned concrete road bridges using artificial neural networks. Structural Multidisciplinary Optimization 56: 139-150.
- Stevanovic, Stevanovic J, Zhang K, Batterman S (2009) Optimizing Traffic Control to Reduce Fuel Consumption and Vehicular Emissions. Transportation Research Record 2128: 105-113.
- Sang C Lhee, Raja RA Issa, Flood I (2016) Using Particle Swarm Optimization to Predict Cost Contingency on Transportation Construction Projects. Journal of Information Technology in Construction 21: 504- 516.
- Sabatino S, Dan M Frangopol, Dong Y (2015) Sustainability-informed maintenance optimization of highway bridges considering multiattribute utility and risk attitude. Engineering Structures 102(8): 310- 321.
- Barone G, Dan M Frangopol, Soliman M (2014) Optimization of Life- Cycle Maintenance of Deteriorating Bridges with Respect to Expected Annual System Failure Rate and Expected Cumulative Cost. Journal of Structural Engineering 140(2): 1-13.
- Cai H, Amjad A Aref (2015) A genetic algorithm-based multi-objective optimization for hybrid fiber reinforced polymeric deck and cable system of cable-stayed bridges. Structural Multidisciplinary Optimization 52: 583-594.
- Cai H, Amjad A Aref (2015) On the design and optimization of hybrid carbon fiber reinforced polymer-steel cable system for cable-stayed bridges. Composites: Part B 68: 146-152.
- Chen Z, Cao H, Ye K, Zhu H, Li S (2015) Improved Particle Swarm Optimization-Based Form-Finding Method for Suspension Bridge Installation Analysis. Journal of Computing in Civil Engineering 29(3): 1-13.
- Silva M, Santos A, Figueiredo E, Santos R, Sales C (2016) A novel unsupervised approach based on a genetic algorithm for structural damage detection in bridges. Engineering Applications of Artificial Intelligence 52: 168-180.
- Liu Y, Chang GL (2011) an arterial signal optimization model for intersections experiencing queue spillback and lane blockage. Transportation Research Part C 19: 130-144.
- Hu H, Henry X Liu (2013) Arterial offset optimization using archived high-resolution traffic signal data. Transportation Research Part C 37: 131-144.
- Sharma R, Kumari A, A Review on Traffic Route Optimizing by Using Different Swarm Intelligence Algorithm. International Journal of Computer Science and Mobile Computing 4 5: 271-277, 2015.
- Xiao C, Ling T, Qiu Y (2013) Optimization of technical measures for improving high-temperature performance of asphalt–rubber mixture. Journal of Modern Transportation 21(4): 273–280.
- Ghanizadeh AR (2016) An Optimization Model for Design of Asphalt Pavements Based on IHAP Code Number 234. Advances in Civil Engineering, pp.1-8.
- Santos J, Ferreira A (2012) Life-Cycle Cost Analysis System for Pavement Management. Procedia - Social and Behavioral Sciences 48: 331-340.
- Koo C, Hong T, Kim S (2015) An integrated multi-objective optimization model for solving the construction time-cost trade-off problem. Journal of Civil Engineering and Management 21(3): 323-333.
- Azeez MN, Alsaffar A (2014) Construction Time-Cost Optimization Modeling Using Ant Colony Optimization. Journal of Engineering 20(1): 114-131.
- Aziz RF, Hefez SM, Abuel-Magd YR (2014) Smart optimization for mega construction projects using artificial intelligence. Alexandria Engineering Journal 53: 591-606.
- Narayanan AS, Suribabu CR (2014) Multi-Objective Optimization of Construction Project Time-Cost-Quality Trade-off Using Differential Evolution Algorithm. Jordan Journal of Civil Engineering 8(4): 375-392.
- Zhang H, Li H (2010) Multi-objective particle swarm optimization for construction time-cost tradeoff problems. Construction Management and Economics 28(1): 75-88, 2010.
- Elbeltagi E, Ammar M, Sanad H, Kassab M (2016) Overall multiobjective optimization of construction projects scheduling using particle swarm. Engineering, Construction and Architectural Management 23(3): 265- 282.
- Bettemir ÖH, Birgönül MT (2017) Network Analysis Algorithm for the Solution of Discrete Time-Cost Trade-off Problem. KSCE Journal of Civil Engineering 21(4): 1047-1058.
- Afshar, Ziaraty AK, Kaveh A, Sharifi F (2009) Nondominated Archiving Multicolony Ant Algorithm in Time–Cost Trade-Off Optimization. Journal of Construction Engineering and Management 135(7): 668-374.
- Aminbakhsh S, Sönmez R (2016) Discrete particle swarm optimization method for the large-scale discrete time–cost trade-off problem. Expert Systems with Applications 51: 177–185.
- Aminbakhsh S, Sönmez R (2017) Pareto Front Particle Swarm Optimizer for Discrete Time-Cost Trade-Off Problem. Journal of Computing in Civil Engineering 31(1): 1-10.
- Sonmez R, Bettemir ÖH (2012) A hybrid genetic algorithm for the discrete time–cost trade-off problem. Expert Systems with Applications 39: 11428–11434.
- Zhang Y, Ng ST (2012) An ant colony system-based decision support system for construction time-cost optimization. Journal of Civil Engineering and Management 18(4): 580-589.
- Ng ST, zhang Y (2008) Optimizing Construction Time and Cost Using Ant Colony Optimization Approach. Journal of Construction Engineering and Management 134(9): 721-728.
- Geem ZW (2010) Multiobjective Optimization of Time-Cost Trade- Off Using Harmony Search. Journal of Construction Engineering and Management 136(6): 711-716.
- Magalhaes-Mendes J (2016) Multiobjective Optimization of Construction Project Time-Cost-Quality Trade-off Using a Genetic Algorithm. WSEAS Transactions on Computers 15: 310-318.
- Rostani M, Moradinezhad D, Soufipou A (2014) Improved and Competitive Algorithms for Large Scale Multiple Resource-Constrained Project-Scheduling Problems. KSCE Journal of Civil Engineering 18(8): 1261-1269.
- Monghasemi S, Nikoo MR, Fasaee MAK (2015) A novel multi criteria decision making model for optimizing time–cost–quality trade-off problems in construction projects. Expert Systems with Applications 42: 3089-3104.
- Choddousi P, Eshtehardian E, Jooybanpor S, Javanmardi A (2013) Multimode resource-constrained discrete time–cost-resource optimization in project scheduling using non-dominated sorting genetic algorithm. Automation in Construction 30: 216–227.
- Tavana M, abtahi AR, Khalili-Damghani K (2014) A new multi-objective multi-mode model for solving preemptive time–cost–quality trade-off project scheduling problems. Expert Systems with Applications 41: 1830-1846.
- Zamarrón-Mieza, V. Yepes, J.M. Moreno-Jiménez (2017) A Systematic Review of Application of Multi-Criteria Decision Analysis for Aging-Dam. Journal of Cleaner Production 147: 217-230.
- Penadés-Plà V, García-Segura T, Martí JV, Yepes V (2016) A Review of Multi-Criteria Decision-Making Methods Applied To The Sustainable Bridge Design. Sustainability 8: 12.
- Bayram A, UzluE, Kankal M, Dede T (2015) Modeling stream dissolved oxygen concentration using teaching–learning based optimization algorithm. Environ Earth Sci 73: 6565-6576.
- Morleya MS, Tricarico C (2014) A comparison of population-based optimization techniques for water distribution system expansion and operation. Procedia Engineering 89: 13-20.
- Eck BJ, Arandia E, Naoum-Sawaya J, Wirth F (2014) A Simulation- Optimization Approach for Reducing Background Leakage in Water Systems. Procedia Engineering 89: 59-68.
- IraniR, NasimiR (2011) Application of artificial bee colony-based neural network in bottom hole pressure prediction in underbalanced drilling. Journal of Petroleum Science and Engineering 78: 6–12.
- Kisi O, OzkanC, Akay B (2012) Modeling discharge–sediment relationship using neural networks with artificialbee colony algorithm. Journal of Hydrology 428–429: 94–103.
- Uzlu E, Kankal M, Akpınar A, Dede T (2014) Estimates of energy consumption in Turkey using neural Networks with the teaching learning-based optimization algorithm. Energy 75: 295-303.
- Karbasi M (2016) Estimation of classical hydraulic jump length using teaching–learning based optimization algorithm. J Mater Environ Sci 7(8): 2947-2954.
- Blinco LJ, Simpson AR, Lambert MF, Auricht CA, Hurr NE, et al. (2014) Genetic Algorithm Optimization of Operational Costs and Greenhouse Gas Emissions for Water Distribution Systems. Procedia Engineering 89: 509-516, 2014.
- Quiniou ML, Mandel P, Monier L (2014) Optimization of Drinking Water and Sewer Hydraulic Management: Coupling of a Genetic Algorithm and Two Network Hydraulic Tools. Procedia Engineering 89: 710 – 718.
- Peralta RC, Forghani A, Fayad H (2014) Multiobjective genetic algorithm conjunctive use optimization for production, cost, and energy with dynamic return flow. Journal of Hydrology 511: 776–785.
- Fayad H, Peralta RC, Forghani A (2012) Optimizing Reservoir-Stream- Aquifer Interactions for Conjunctive Use and Hydropower Production. Advances in Civil Engineering:1-10.
- Bahrami S, Ardejani FD, Baafi E (2016) Application of artificial neural network coupled with genetic algorithm and simulated annealing to solve groundwater inflow problem to an advancing open pit mine. Journal of Hydrology 536: 471–484.
- Luo Q, Wub J, Yang Y, Qian J, Wu J (2014) Optimal design of groundwater remediation system using a probabilistic multi-objective fast harmony search algorithm under uncertainty. Journal of Hydrology 519: 3305– 3315.
- Yang Y, Wu J, Sun X, Wu J (2013) Chunmiao Zheng, A niched Pareto tabu search for multi-objective optimal design of groundwater remediation systems. Journal of Hydrology 490: 56–73.
- Yaseen ZM, Ebtehaj I, Bonakdari H, Deo RC, Mehr AD, et al. (2017) Novel approach for streamflow forecasting using a hybrid ANFIS-FFA model. Journal of Hydrology 55: 4263–276.
- Jalili S, Hosseinzadeh Y (2015) A Cultural Algorithm for Optimal Design of Truss Structures. Latin American Journal of Solids and Structures 12: 1721-1747.
- Cicconi P, Germani M, Bondi S, Zuliani A, Cagnacci E (2016) A Design Methodology to Support the Optimization of Steel Structures. Procedia CIRP 50:58-64, 2016.
- Medeiros GF, Kripka M (2013) Structural optimization and proposition of pre-sizing parameters for beams in reinforced concrete buildings. Computers and Concrete 11(3): 253-270.
- Kaveh, Talatahari S (2009) A particle swarm ant colony optimization for truss structures with discrete variables. Journal of Constructional Steel Research 65(8–9): 1558-1568.
- Souza RR, Miguel LFF, Lopez RH, Miguel LFF, Torii AJ (2016) A procedure for the size, shape and topology optimization of transmission line tower structures. Engineering Structures 111: 162-184.
- Dede T, Ayvaz Y (2015) Combined size and shape optimization of structures with a new meta-heuristic algorithm. Applied Soft Computing 28: 250-258.
- Pholdee N, Bureerat S (2014) Comparative performance of metaheuristic algorithms for mass minimisation of trusses with dynamic constraints. Advances in Engineering Software 75:1-13.
- Alapati M (2014) Discrete Optimization of Truss Structure Using Genetic Algorithm. International Journal of Recent Development in Engineering and Technology 3: 105-111.
- Chowdhury MA, Islam MM, Zahid ZI (2016) Finite Element Modeling of Compressive and Splitting Tensile Behavior of Plain Concrete and Steel Fiber Reinforced Concrete Cylinder Specimens. Advances in Civil Engineering 2016: 1-11.
- Farshchin M, Camp CV, Maniat M (2016) Multi-class teaching–learningbased optimization for truss design with frequency constraints. Engineering Structures 106: 355-369.
- Talaslioglu T (2011) Multiobjective Design Optimization of Grillage Systems according to LRFD-AISC. Advances in Civil Engineering 211: 1-24.
- Belevicius R, Jatulis D, Rusakevicius D, Maciunas D (2017) Optimization of Rigidly Supported Guyed Masts. Advances in Civil Engineering 2017: 1-9.
- Poitras G, Lefrançois G (2011) Cormier Optimization of steel floor systems using particle swarm optimization. Journal of Constructional Steel Research 67(8): 1225-1231.
- Dede T (2013) Optimum design of grillage structures to LRFD-AISC with teaching-learning based optimization. Struct Multidisc Optim 48: 955-964.
- Kaveh, Bakhshpoori T (2013) Optimum Design of Space Trusses Using Cuckoo Search Algorithm with Lévy Flights. IJST, Transactions of Civil Engineering 37: 1-15.
- Hasançebi O, Çarbaş S, Doğan E, Erdal F, Saka MP (2009) Performance evaluation of metaheuristic search techniques in the optimum design of real size pin jointed structures. Computers & Structures 87(5-6): 284-302.
- Sharafi P, Lip H Teh, Muhammad, Hadi S (2014) Shape optimization of thin-walled steel sections using graph theory and ACO algorithm. Journal of Constructional Steel Research 101: 331-341.
- Fabeane R, Kripka M, Pravia ZMC (2017) Composite Bridges: Study of Parameters to Optimized Design. International Journal of Bridge Engineering 5(2): 1-20.
- Majumdar, Nanda B, Maiti DK, Maity D (2014) Structural Damage Detection Based on Modal Parameters Using Continuous Ant Colony Optimization. Advances in Civil Engineering 2014: 1-14.
- Torres-Machi, Yepes V, Alcalá J, Pellicer E (2013) Optimization of high-performance concrete structures by variable neighborhood search. International Journal of Civil Engineering, Transaction A: Civil Engineering 11(2): 90-99.
- Rao R, More KC (2017) Design optimization and analysis of selected thermal devices using self-adaptive Jaya algorithm. Energy Conversion and Management 140: 24-35.
- Oclon P, Cisek P, Rerak M, Taler D, Rao RV, et al. (2018) Thermal performance optimization of the underground power cable system by using a modified Jaya algorithm. International Journal of Thermal Sciences 123: 162-180.
- Rao RV, Rai DP, Balic J (2017) A multi-objective algorithm for optimization of modern machining processes. Engineering Applications of Artificial Intelligence 61: 103-125.
- Apalak MK, Yildirim M, Ekici R (2008) Layer optmisation for maximum fundamental frequency of laminated composite plates for different edge conditions. Composites Science and Technology 68(2): 537-550.
- Koide RM, von Z de França G, Luersen MA (2013) an ant colony algorithm applied to lay-up optimization of laminated composite plates. Latin American Journal of Solids and Structures 10: 491 – 504.
- Honda S, Narita Y, Sasaki K (2009) Discrete Optimization for Vibration Design of Composite Plates by Using Lamination Parameters. Advanced Composite Materials 18: 297–314.
- Topal U, DedeT, Öztürk HT (2017) Stacking Sequence Optimization for Maximum Fundamental Frequency of Simply Supported Antisymmetric Laminated Composite Plates using Teaching–Learning- Based Optimization. KSCE Journal of Civil Engineering 266: 2281- 2288.
- Thamaraikannan B, ThirunavukkarasV (2014) Design Optimization of Mechanical Component Using an Enhanced Teaching-Learning Based Optimization Algorithm with Differential Operator. Mathematical Problems in Engineering, Hindawi Publishing Corporation 2014:1-10.
- Kaveh A, Talatahari S (2010) Optimal design of skeletal structures via the charged system search algorithm. Structural and Multidisciplinary Optimization.
- Kaveh A, Talatahari S (2010) Charged system search for optimum grillage system design using the LRFDAISC code,Journal of Constructional Steel Research 66(6): 767-771.
- Kaveh and S Talatahari S (2010) Optimal design of Schwedler and ribbed domes via hybrid Big Bang-Big Crunch algorithm. Journal of Construction Steel Research 66(3): 412-419.
- Camp V (2007) Design of space trusses using big bang-big crunch optimization. Journal of Structural Engineering 133(7): 999-1008.
- Narayanan AS, Suribabu CR (2014) Multi-Objective Optimization of Construction Project Time-Cost-Quality Trade-off Using Differential Evolution Algorithm. Jordan Journal of Civil Engineering 8(4): 375- 392.
- Yusup N, Zain AM, Hashim SZM (2012) Overview of PSO for optimizing process parameters of machining. Procedia Engineering 29: 914-923.
- Apalak MK, Karaboğa D, Akay B (2014) The Artificial Bee Colony algorithm in layer optimization for the maximum fundamental frequency of symmetrical laminated composite plates. Engineering Optimization 46(3): 420-437.
- Karakaya Ş, Soykasap Ö (2011) Natural frequency and buckling optimization of laminated hybrid composite plates using genetic algorithm and simulated annealing. Structural Multidisciplinary Optimization 43: 61-72.
- Sadr MH, Bargh HG (2012) Optimization of laminated composite plates for maximum fundamental frequency using Elitist-Genetic algorithm and finite strip method. Journal of Global Optimization 54: 707-728.
- Anh LL, Thoi TN, Huu VH, Trung HD, Xuan TB (2015) Static and frequency optimization of folded laminated composite plates using an adjusted differential evolution algorithm and a smoothed triangular plate element. Composite Structures 127(1): 382-394.
- Vosoughi R, Nikoo MR (2015) Maximum fundamental frequency and thermal buckling temperature of laminated composite plates by a new hybrid multi objective optimization technique. Thin Walled Structures 95(32): 408-415.
- Nourbakhsh, Safikhani H, Derakhshan S (2011) The comparison of multi-objective particle swarm optimization and NSGA II algorithm: applications in centrifugal pumps. Engineering Optimization 43(10): 1095-1113.
- Venkata Rao R, Waghmare G (2015) Design optimization of robot grippers using teaching-learning-based optimization algorithm. Advanced Robotics 29(6): 431-447.
-
Tayfun Dede, Moacir Kripka, Vedat Togan, Victor Yepes, R Venkata Rao. Usage of Optimization Techniques in Civil Engineering During the Last Two Decades. Cur Trends Civil & Struct Eng. 2(1): 2019. CTCSE.MS.ID.000529.
-
Optimization techniques, Optimization algorithms, Civil engineering, Review, Topology, Discrete, Genetic algorithms, Particle swarm optimization, Temperature
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






