 Research Article
Research Article
Steel-Concrete Interface Influence on Chloride Threshold for Corrosion – Empirical Reinforcement to Theory
Amit Kenny1* and Amnon Katz2
1Current address: Civil engineering department, Shamoon College of engineering, 84 Jabotinski St. Ashdod 77245 Israel
2Faculty of civil and environmental engineering, Technion - IIT, Haifa, 32000 Israel; National Building Research Institute, Technion - IIT, Haifa, 32000 Israel
Amit Kenny, Shamoon College of engineering, 84 Jabotinski St. Ashdod, Israel.
Received Date: November 10, 2019; Published Date: November 18, 2019
Abstract
Reinforcement corrosion is a common cause for reinforced concrete structure deterioration. One of the main causes for reinforcement corrosion is chloride ingress to the concrete. Published work hints a relationship between the susceptibility to chloride induced corrosion, referred as the chloride threshold, which is the chloride concentration at corrosion initiation, and the interface between the concrete and the rebar, known as interfacial transition zone (ITZ). This paper presents an investigation of the relationship between the chloride threshold for chloride-induced corrosion and the properties of the ITZ around embedded rebar was investigated using 16 different concrete mixes. ITZ properties were extracted using automated image analysis. The chloride threshold was found to decrease with the distance between the rebar surface and the concrete solids. In the case of horizontal rebar, the chloride threshold decreases with ITZ thickness as well. These results agree with the theory of concentration polarization in localized corrosion and may explain the variety of chloride threshold values reported in the literature.
Keywords: Concrete; Chloride threshold; Rebar; Corrosion; Interfacial transition zone
Abbreviations: BSE: Back Scattered Electron Microscopy; CCCL: Chloride Corrosion Concentration Limit or Chloride Threshold; EIS: Electrochemical Impedance Spectroscopy; HRWR: High Range Water Reducer; ITZ: Interfacial Transition Zone; RC: Reinforced Concrete
Introduction
Corrosion damage is typically the biggest item on the maintenance bill of reinforced concrete (RC) structures. In the USA, direct costs due to corrosion of RC infrastructures are estimated at 0.25% of the GNP, which corresponds to $16.6 billion a year [1]. Chloride-induced corrosion is the main cause for corrosion damages in bridges in the USA [2]. When the chloride content near the rebar surface exceeds a certain limit, referred to as the chloride corrosion concentration limit (CCCL, also denoted as “threshold” in the followings), depassivation of the steel occurs and the steel is susceptible to corrosion; indeed, the corrosion hazard to the embedded reinforcement increases drastically above this level [3]. Most of the attention in research and practice is directed towards reducing the rate of chloride ingress into the concrete by reducing concrete permeability and increasing the transport length (increased concrete cover) [4-7]. A change in the chloride threshold can have a much larger effect on the lifetime of RC than do the transport properties of the concrete or the cover Crete thickness. Thus, for example, according to LIFE-365 model [8], a 20% increase in CCCL increases the time to initiation of corrosion by 28%, whereas a 20% reduction in the diffusion coefficient increases the time to initiation of corrosion by only 10%. The range of chloride threshold values presented in the literature is wide and includes [C-]/[OH-] ratio ranging from 0.12 to 3.0; 0.03% to 4% free chloride from cement mass; and 0.04% to 2.42% total chloride from cement mass [9-18]. It is difficult to compare the various results since it is not always possible to convert from one representation method to another due to missing data in the reported works. The considerable spread of chloride threshold values encountered in the literature may be the result of the high number of variables that influence the chloride threshold such as cement chemical composition, temperature, steel composition, to name but a few [16], [19]. Investigation of steel bars embedded in simulated pore solution containing various concentrations of chlorides offers a more reliable representation of the chemical processes that take place between the chloride ions and steel surface. This synthetic situation does not, however, represent the true situation that occurs in concrete that contains voids, aggregates, and chlorides of different availability (i.e. free and bound). Inconsistent investigation of the variables and published data make it difficult to extract reliable information about the influencing variables. Thus, determination of the most appropriate method to represent the chloride threshold value is, in itself, controversial. Angst and Vennesland [17] reviewed the pros and cons of several representation methods, namely free chlorides and total chlorides, and chloride concentration relative to cement, total binder, concrete and [OH-]. All methods are presented in the literature, but no conclusion is reached as to the preferred method.
Several authors emphasized surface voids on the steel as the main durability-related problem of reinforced concrete. Observations of corroding RC structures show that corrosion initiates at these voids and that good quality of the steel-concrete interface can delay initiation of corrosion [20-24]. Glass and Reddy [25] found that the chloride threshold rises sharply when the percent of voids drops below 2% of the interface surface. In their work, they intentionally created voids by applying insufficient vibration to low slump concrete. These voids were, however, macroscopic and do not offer a good simulation of the true situation in well-consolidated concrete. In addition to the void size itself, various solid precipitants are present on the steel surface. For example, Glass et al. [26] concluded that hydration products found on steel surface are similar to those in the bulk cement paste, whereas Horne et al. [27] concluded that these products are actually all calcium hydroxide, but at different concentrations that vary also between vertical or horizontal oriented bars. The influence of voids on the corrosion behavior of embedded steel can be understood through the localized corrosion mechanism. Galvele [28] proposed a model for the concentration polarization of pH between a metal surface within a pit and an aqueous buffer solution over the pit opening. For a specific corrosion rate, the pH at the metal-solution interface decreases as the distance between the metal and the buffer increases, and the metal is at greater risk for a higher corrosion rate. Since concrete is a strong buffer at high pH values, we can infer that the risk for corrosion increases with the distance between the steel and the concrete. Thus, for every single point on the steel surface, the distance to the closest concrete component determines its susceptibility to localized corrosion. The point at which this distance is maximal will be the most susceptible to corrosion and will determine the resistance to corrosion. Parameters of minimal distance between the steel and the concrete are, therefore, considered to be an important characteristic of the interfacial transition zone (ITZ) with respect to RC durability. The above short review demonstrates the difficulties involved in isolating the various parameters that affect the initiation of steel bar corrosion in reinforced concrete. This paper presents a statistical analysis of the relationships between the chloride threshold and ITZ properties, mix composition, and fresh mix properties. An unbiased statistical method was used to eliminate biased interpretation of the results. Sixteen different concrete mix compositions were prepared in which steel was embedded in two directions to produce a range of ITZ structures. Over 1,300 images were analyzed using an automated image analysis developed for this study [29]. The results were used to identify possible relationships between chloride threshold limit and ITZ parameters that are affected by mix composition and fresh mix properties as published in [30]. The model proposed by [28] was applied in a modified way, where the steel-concrete distance at the steel concrete interface represents the distance from a buffer in Galvele model and was used in the current work to explain the corrosion results.
Experimental
Mix preparation
Sixteen different concrete mixes were produced. Variations in mix properties were intended to create variety of rebar-concrete interface, while keeping constant chemistry. The mix variables were: (1) w/c ratios between 0.40 and 0.65; (2) water / powder ratios ranging from 0.91 to 1.36 at constant w/c ratios of either 0.45 or 0.52 where the powders include all the particles smaller than 0.15 mm, which makes part of the aggregates. The amount of powders was adjusted by adding fine lime powder. The mixes were designed to yield different ITZ properties. The composition of the concrete mixes is given in Table 1. The concrete was mixed according to the following procedure: coarse aggregates were premixed with 70% of total water for 1 min. and allowed to absorb water for an additional 5 min in rest. Fine aggregates, cement, powder, the rest of the water, and admixture were then added and mixed for an additional 3 min. Other mix properties are described in detail elsewhere [30]. Mix notation: The letter W followed by two digits represents the water to cement ratio; the letter C (in some mixes) followed by two digits represents addition of fine lime powder expressed as percent of cement weight. The letters H and V represent rebar orientation relative to cast direction-horizontal or vertical, respectively. Thus, for example, W45C16-H denotes a sample with a w/c ratio of 0.45, added lime powder at a ratio of 16% of cement weight, and horizontal rebars (relative to cast direction). Mix W40 was cast twice. The second cast was notated as W40B2.
Table 1: Concrete mix compositions per 1 m3.
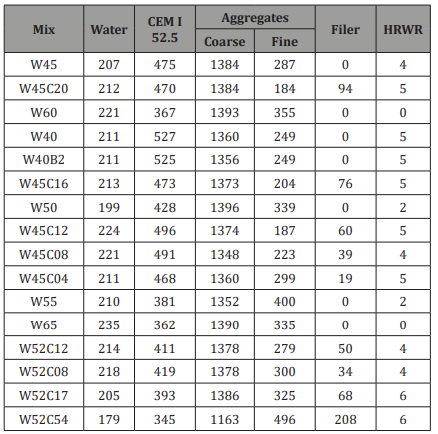
Specimen preparation
Special attention was taken to assure uniform rebar preparation. All rebars were treated similarly prior to casting, as follows: immersion in H3PO4SUB> 10% for two hours, washing and brushing under hot water, hot air drying, immersion in saturated Ca(OH)2 solution for 24 hours, drying, and positioning and fixing in molds. This procedure, which create different rebar surface than ribbed “as-received” condition, was used to reduce variability, to enable focusing on the research objective. To allow different types of ITZs to form, two types of molds were prepared for each concrete mix, with rebars in either horizontal or vertical orientation, with respect to cast direction. Specimen dimensions were 150 mm x 150 mm x 230 mm and net distance between rebars was 65mm (Figure 1).
Two duplicates were prepared for each rebar orientation. All specimens were cured in water at 20°C for one week and for an additional 21 days at 20°C, 100% RH. After casting and curing, the exposed rebar tips were protected against corrosion to a depth of 20mm into the concrete and wired for corrosion measurements. Scheme of rebar tip protection is shown in Figure 2 (Figure 2).
Uniform concrete cover was achieved by sectioning the concrete at a distance of 10±2mm from one of the rebars. This rebar was exposed to penetration of salt whereas the other rebar was used as reference. The side surface of the concrete close to the sectioned face was coated with room temperature vulcanization (RTV) silicone to ensure unidirectional penetration of the solution (Figure 1c).

Corrosion test
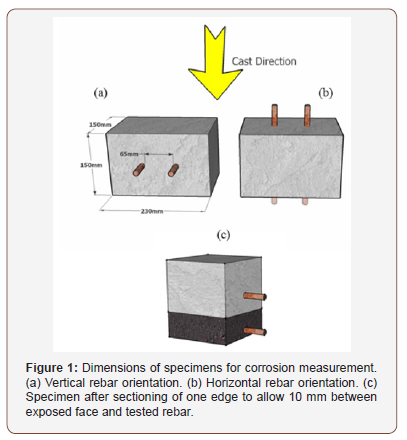
The sectioned face of the specimens was subjected to cycles consisting of two weeks immersion to a depth of 5 mm in a 6% (w/w) NaCl solution (Figure 3) followed by two weeks air-drying at 30°C, 30% RH. Corrosion initiation was monitored by measuring the potential difference between the upper and lower rebars of each concrete specimen. The lower rebar was closer to the chloride source and so corrosion was expected to initiate there. The upper rebar was used as an internal reference. Potential was measured against an Ag|AgCl half-cell for validation. A shift in potential of more than 100 mV in one day, relatively both to the internal reference and the Ag|AgCl half-cell, were taken to indicate the breakdown of the passivation layer protecting the steel. Samples for chloride measurements were taken at that time and immersion to chlorides has stopped. The potential shift indicating corrosion initiation was validated by analyzing several specimens using electrochemical impedance spectroscopy (EIS), which Ann and Song [16] considered to be the method that gives the most accurate information on corrosion. Good correlation was obtained between the two measuring methods, validating the potential shift results (Figure 3).
All the specimens were split for visual inspection and corrosion validation several months after corrosion initiation (Figure 4). Results from specimens that did not exhibit visible signs of corrosion during the visual inspection or that exhibited corrosion in the electrochemical tests shortly after the initiation of the corrosion test (<14 days) were omitted from the data analysis (Figure 4).

Chloride measurement
The following procedure was used to determine the free chloride concentration in the concrete. Free chloride was chosen since no carbonation or other acidification is involved in the research objective. Upon detection of active corrosion, sixteen 4 mm bores were drilled in each specimen, along a line parallel to the corroding rebar, 10mm from the exposed surface. Powder from the bores was collected and 2 g concrete powder was mixed with 40 ml distilled water, shaken for 2 hours, and allowed to settle for an additional 24 hours. Twenty ml of the supernatant fluid was acidified by adding 1 ml HNO3 1M and the chloride concentration of the solution was measured using an ion-selective electrode device. Free chloride content was determined first as ‰ (1/1000) of concrete weight, and later calculated as % cement based on the known mix composition. In addition, OH- concentration of the concrete pore-solution was calculated using the model proposed by Taylor [31], and the ratio [Cl-]/[OH-] was determined accordingly.
ITZ characterization
Back-scattered electron (BSE) images were taken from the areas all around the rebar of every mix and every rebar orientation. BSE images were analyzed automatically, as described in [29]. In short, two slices of 30 mm x 30 mm x 5 mm each were prepared for each mix/orientation. The slice prepared perpendicular to the rebar longitudinal axis to show its cross-section and the surrounding concrete. After epoxy impregnation and polishing, the entire perimeter was scanned at x 100 magnification to yield high-resolution image in which each pixel corresponds to ~0.65 mm. A total of ~1300 BSE images from 16 mixes and two rebar orientations were scanned and analyzed using the modified mean shift algorithm to properly cluster the pixels into the right phase (concrete, steel or air, Figure 5). The following ITZ properties were obtained for each image:
1. ITZ thickness: distance from rebar surface to the bulk matrix
2. Porosity: sum of pixels clustered as pores divided by the sum of pixels in the ITZ of a certain image.
3. Maximal porosity: the largest porosity value obtained from all the images around each rebar.
4. Steel-concrete distance: the distance from rebar surface to the nearest concrete particle. Note that steel-concrete distance represents the distance from the steel surface to the nearest concrete solid, including solid deposits on the steel surface, whereas ITZ thickness represents the thickness of the entire ITZ to the bulk concrete matrix. The statistical data (maximum value, average, and standard deviation) for each parameter were also recorded. The obtained data were aggregated by concrete mix and rebar orientation (Figure 5).

Data analysis
Data analysis was performed using an objective statistical tool to verify relationships between mix composition or fresh mix properties and ITZ variables. The two parameters calculated were correlation coefficient and p-value. The correlation coefficient, which reflects the noisiness and direction of a relationship between two parameters, or the explained variability, was used here to indicate the existence or absence of relationships between the investigated variables. No correlation exists when the coefficient equals or is close to zero, and good correlation is indicated when the coefficient is close to 1 or -1 for direct or inverse correlations, respectively. Although the correlation coefficient may clearly indicate a tendency, as long as the relationship is monotonous, it tells us nothing about the relationship type (e.g. linear or logarithmic). p-values were used here to validate the significance of the correlation coefficients. A p-value represents the probability of obtaining a correlation coefficient from random data that is at least as valid as the p-value calculated for experimental data. This method takes in account the number of observations, hence allow statistical analysis even with restricted number of observations. P-value smaller than 0.05 indicates that the correlation is statistically significant at a confidence level greater than 95%. Statistical methods are frequently used in concrete studies to determine the significance of correlations among variables that cannot be isolated and identified separately [32-34].
Results and Discussion
Table 2 presents average chloride threshold values obtained for specimens that exhibited both corrosion potential after more than two weeks and corrosion in the visual examination. Specimens that did not show these two signs of corrosion were excluded from the analysis. The chloride threshold ranged from 0.56‰ concrete to 7.98‰ concrete, or 0.28% to 5.12% cement (Table 2), values that are in agreement with published data. The highest chloride threshold was found in the concrete mix with the highest water to cement ratio. The average chloride threshold was 4.16‰ concrete, or 2.26% cement and the average threshold was 3.7‰ concrete for horizontal rebars and 4.2‰ concrete for vertical rebars. However, the t-test yielded a p-value of 0.40, indicating that the difference between the two rebar orientations is insignificant. Examination of the threshold values for the two rebar orientations in same-mix specimens failed to reveal a consistent trend, i.e. in some mixes the threshold value for vertical bars was higher than for horizontal bars, and in other mixes it was lower (Figure 6) (Table 2).
Table 2: Chloride threshold for the different mixes and rebar orientations (free chloride, only for specimens that exhibited corrosion).
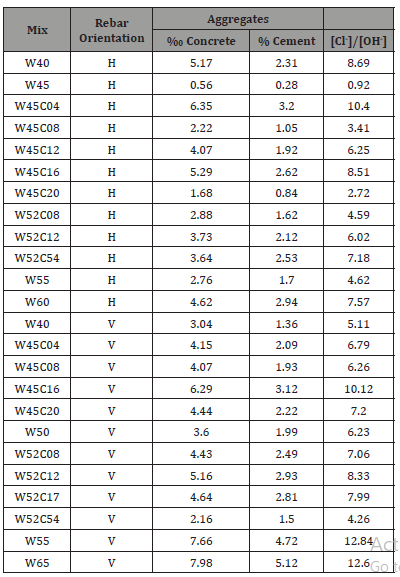
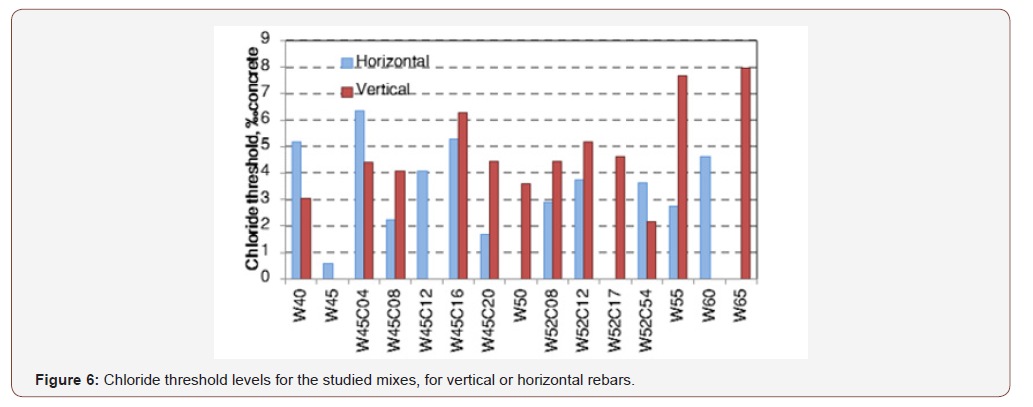
Relatively high values (up to 12.8) are obtained when the results are expressed as [Cl-]/[OH-]. Values reported in the literature (e.g. review in [16,17]) for the corrosion of steel rebars immersed in simulated pore solution were lower than 1.0. Low values were recorded also for rebars embedded in mortars in which chloride constituted part of the mixing water. Higher values were, however, obtained when the chlorides were not part of the mixing water but rather diffused into the concrete from the environment. Yonezawa et al. [35] presented ratio values as high as 60 for rebars embedded in mortar that had good contact with the steel, whereas
much smaller values were obtained in a simulated pore solution. The appropriate representation method of CCCL was addressed in detail in the literature and no consensus has been reached. The ratio [Cl-]/[OH-] represents the theoretical chemistry of steel embedded in a solution containing chloride ions, but the situation in real concrete is more complicated. Therefore, ‘percent of cement content’ is used more often and a CCCL value of ~0.2% cement is used widely in various standards as the limiting value for chlorides in new concrete. The determination of chlorides as % cement in concrete is done by measuring the chloride content of a concrete sample and calculating its percentage relative to the cement, where cement content is known or determined experimentally. The selection of the appropriate representation method is important for understanding the parameters that influence CCCL. CCCL was, therefore, calculated as % concrete (the initial measurement), % cement (calculated based on the known cement content) and [Cl-]/ [OH-] (calculated according to Taylor’s model [31] using the actual w/c and cement contents). Statistical analysis of the results yielded a correlation between CCCL, expressed by the three representation methods, and concrete mix variables such as water and cement, which determine the chemistry of pore water, and powder content, which affects the properties of the fresh mix. The following assumptions were tested:
1. If the ratio between CCCL and cement is constant, then CCCL values expressed as % concrete is expected to increase with the increase in cement content of the mix (positive correlation) while zero correlation is expected when CCCL is expressed as % cement. The opposite behavior is expected if the ratio between CCCL and concrete mass is constant, i.e. a negative correlation exists between CCCL and cement content when CCCL is expressed as % cement.
2. Calculation according to the critical [Cl-]/[OH-] is more complicated since lowering the w/c ratio or increasing the cement content increases OH- concentration in the pore water and so [Cl-] threshold is expected to increase as well, if [Cl-]/[OH- ] is assumed to be a constant value. When, however, concrete is prepared with a lower w/c ratio, the total amount of pore water is reduced, leading to a lower OH- content per concrete unit mass or volume, and to a reduced Cl- content accordingly, for a constant [Cl-]/[OH-] in the pore solution. According to Taylor’s model, OH- content falls within a narrow range, between ~39 and ~41 mole/(m3 concrete) for most of the mixes evaluated in this study. Therefore, correlations similar to those found for ‰ concrete are expected.
The results are presented in Table 3; correlations with p-values smaller than 0.05 are emphasized. Significant correlations (p-value<0.05) were found between mix ingredients and CCCL when specimens with both rebar orientations were analyzed together, but no significant correlation was found when specimens with horizontal rebars were analyzed separately (Table 3). Positive correlations between CCCL, expressed as % cement, and w/c and w/p ratios were observed in vertical rebars, and negative correlations were observed, accordingly, between CCCL and cement and powder contents. When CCCL was expressed as ‰ concrete, positive correlation was observed with water content and, accordingly, with w/c and w/p ratios. Negative correlation was exhibited between CCCL and powder content, but not with cement content, although cement constitutes a large share of the powders in the mix. For horizontal rebars no correlation was observed (Table 3).
Table 3: Correlation coefficients of the chloride threshold level with concrete (correlations with p-values below 0.05 are emphasized).
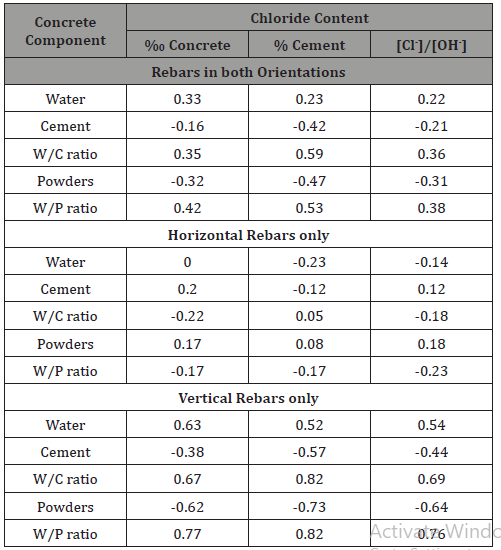
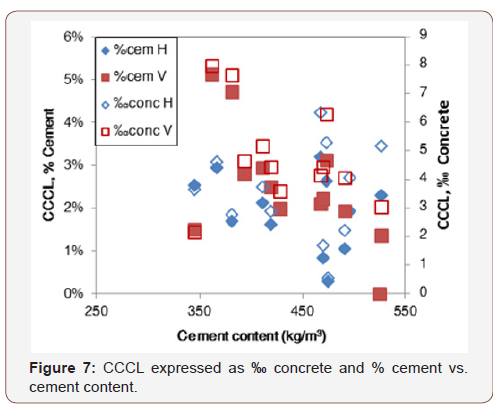
Two examples of such analyses are presented in Figures 7 & 8, for correlations with cement content and water-to-cement ratio, respectively. As can be seen in Figure 6, CCCL (in both expression forms) decreases when cement content increases in specimen with vertically oriented bars but not when bars are horizontal. Figure 8 displays a similar trend: CCCL values increase as w/c ratio increases (lower cement content) in specimen with vertical bars. The statistical analysis, however, yielded a correlation coefficient of -0.38 with a p-value of 0.20 for the correlation between CCCL (‰ concrete) and cement content, indicating that this correlation is insignificant, whereas a p-value of 0.01 was obtained for the correlation with w/c ratio, indicating a significant correlation (Figures 7 & 8).
The results for CCCL expressed as [Cl-]/[OH-] (Table 3) are similar to those obtained for ‰ concrete, indicating that when dealing with real concrete, results expressed in these two representation units are similar, as expected. Indeed, these results show that CCCL for horizontal rebars is not related to cement content or to w/c ratio and that other parameters probably control the chloride threshold for such rebars. The CCCL in specimen with vertical rebars decreases as cement or powder contents increase and when CCCL is expressed as % cement, contradicting the common conception that CCCL is a constant proportion of cement content. The correlations observed between CCCL (‰ concrete) and water and powder contents as well as with w/c and w/p ratios, together with the results discussed above, indicate that when rebars are embedded in real concrete, the corrosion mechanism is more complicated than that exhibited when rebars are immersed in a simulated pore solution containing chlorides or in neat cement paste. In addition, there is a significant difference between vertical and horizontal bars when the effect of w/c ratio is concerned. It is possible that the chemistry and microstructure of the concrete closest to the steel surface influence CCCL values, as will be discussed in the second part of this paper. In the following analysis and discussion, the chloride threshold is presented as permil (‰) of the concrete mass (g Cl-/kg concrete), unless otherwise noted (Table 3).
Correlation between CCCL and ITZ and other fresh mix properties
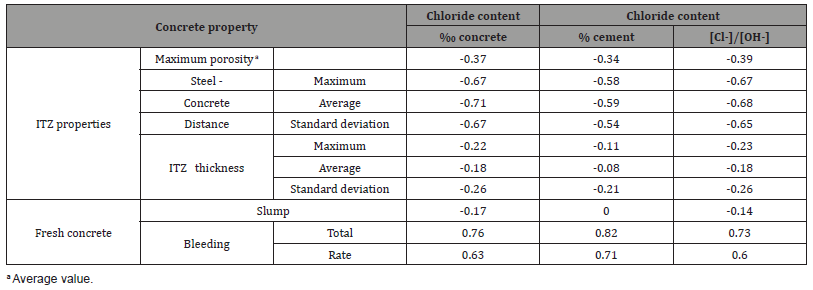
ITZ properties of the steel-concrete interface were determined for both rebar orientations in the various mixes. Following is a short summary of a comprehensive study [30] of the parameters of mix composition and fresh mix properties that affect the ITZ. Table 4 presents the ITZ properties of the mixes included in the corrosion study. Correlation analysis was performed between CCCL and these parameters to identify statistically based relationships and identify parameters that affect the CCCL. Table 5 presents results of this analysis for both rebar orientations, and Tables 6 and 7 present results for horizontal and vertical rebars, respectively (Tables 4-7).
Table 4: ITZ properties by concrete mix.

Table 5: Correlation coefficients for CCCL with respect to concrete and ITZ properties, for both rebar orientations (correlations with p-values below 0.05 are emphasized).
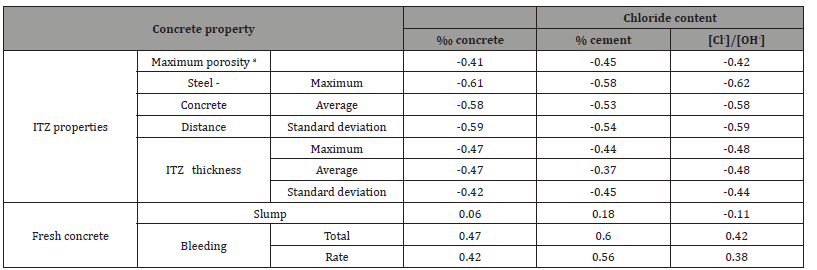
Table 6: Correlation coefficients of CCCL with respect to concrete and ITZ properties, for horizontal rebar (correlations with p-value below 0.07 are emphasized).
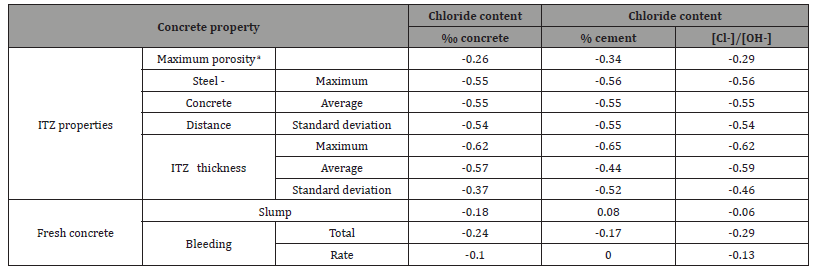
Table 7: Correlation coefficients of CCCL with respect to concrete and ITZ properties, for vertical rebar (correlations with p-value below 0.05 are emphasized).
ITZ properties from image analysis
Table 4 presents ITZ properties of the different concrete mixes and rebar orientations. The maximum porosity for all specimens with horizontal rebars is practically one, due to a large void located beneath the rebar. Average porosity, which was measured around the entire rebar perimeter, is lower since it includes also the areas above and below the rebar. ITZ thickness below horizontal rebars ranged between 186 μm and 320 μm and was not correlated with mix composition or any fresh mix properties. ITZ thickness variability, on the other hand, was correlated with parameters associated with bleeding. Average ITZ thickness around vertical rebars range from 85 μm to 141 μm, which is less than around horizontal rebars, and was not correlated with any of the mix parameters. Steel-concrete distance (from the steel surface to the nearest solid particle, which consists, usually, of various precipitants on the steel surface) was in the order of 10 μm and seems to be inuenced by processes related to hydration and adhesion of particles to the steel surface, thus not correlated to mix properties.
Influence of fresh mix properties on the CCCL
No correlation was found here between CCCL and the workability of fresh mix, i.e. controlling the workability of the fresh mix offers no advantage with respect to CCCL. This conclusion is valid for both rebar orientations (Tables 5-7, Figure 7, and Figure 8). Correlation between CCCL and the bleeding properties of the fresh mix, with p-value<0.05, was found only for the vertical rebar orientation. The correlation coefficient was 0.76 with respect to total bleeding and 0.63 with respect to bleeding rate, which means that CCCL increases when rebars are in vertical orientation and the fresh mix is characterized by greater bleeding. Bleeding parameters were found to be positively correlated with more workable concrete (slump) and water content, and inversely correlated with cement or powder contents. Positive correlation, between CCCL (‰ concrete) and water content for vertical rebars, was described before, and so it is not clear which of the two parameters (water content or bleeding) actually influences the CCCL.
Influence of steel-concrete distance on the CCCL
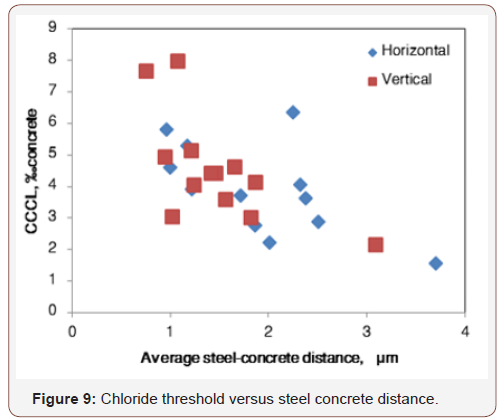
Correlation values for steel-concrete distance and chloride threshold were found to be the most significant compared with other concrete properties: they were high for each of the rebar orientations separately as well as when orientation was not taken into account , and for all chloride presentation methods (Tables 5-7 and Figure 9). The p-value for this correlation was 0.01 when calculated for vertical rebar and for both orientations together, and 0.07 when calculated for horizontal rebar separately; i.e. the probability that steel-concrete distance and chloride threshold are indeed correlated is 99% and 93%, respectively, and about 60% of the variation of the chloride threshold in this study may be attributed to variation in maximum steel-concrete distance . The correlation of CCCL with steel-concrete distance is negative; i.e. larger steel-concrete distance reduces the CCCL (Figure 9).
The correlation between the chloride threshold and the steelconcrete distance can be described by the localized corrosion model published by Galvele [28]. This model describes a pit that corrodes only at its bottom and has a constant chemical environment outside. In analogy to this model, the distance between the steel surface and the closest concrete solid particle (steel-concrete distance) can be considered as the pit depth, and the concrete solids as the phase that produces the constant chemical environment outside the pit (Figure 10).
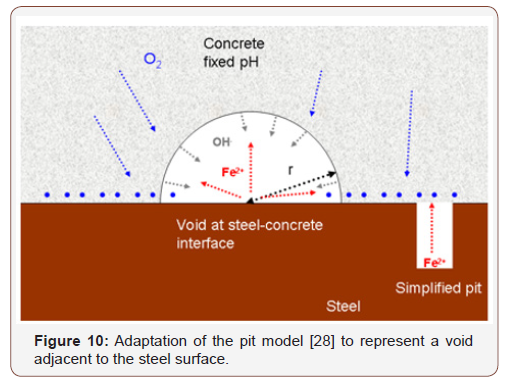
The pit is assumed to be saturated and ions can move freely from one side to the other thus it is reasonable to believe that it is valid for void size of up to some hundreds of microns or so. Based on Galvele’s model, Figure 11 shows the critical product of pit depth and current density for some pH values outside the pit that are typical to concrete phases. The critical product is defined as the point at which the pH value inside the pit drops below 10, i.e. the value at which iron begins to passivate [36]. The critical product of pit depth and current density were calculated as a function of the pH outside the pit (Figure 12). Table 9 presents the critical pH values of typical concrete phases that might be present on the steel surface [37]. It appears that this value changes by about one order of magnitude for any change of one pH unit above pH=10 (Figure 12), up to about 10-5 A/m for pH=13 outside the pit, which can be expected for cement paste [38] (Figures 11,12) (Table 9).
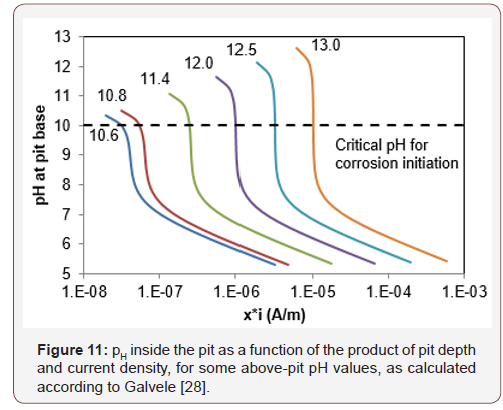
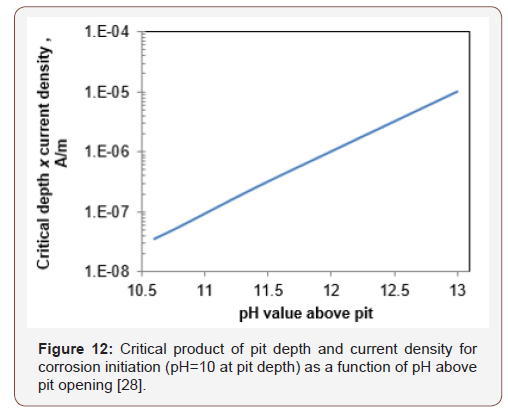
By fixing the pit depth at 10 μm, which is the order of magnitude of the steel-concrete distance, and calculating the current density at base of the pit, which is needed to obtain a pH of 10 at the pit base (critical current density), a result of 1 A/m2 is obtained. The maximal steel-concrete distance was found to vary from 9 to 97 μm and so for the same external pH, the steel-concrete distance at the expected corrosion initiation point, may be 10 times greater than the average distance. As a result, current density, for concentration polarization at a certain point, may be as low as 0.1A /m2 to preserve a constant depth-current density product.
Influence of ITZ thickness on the CCCL
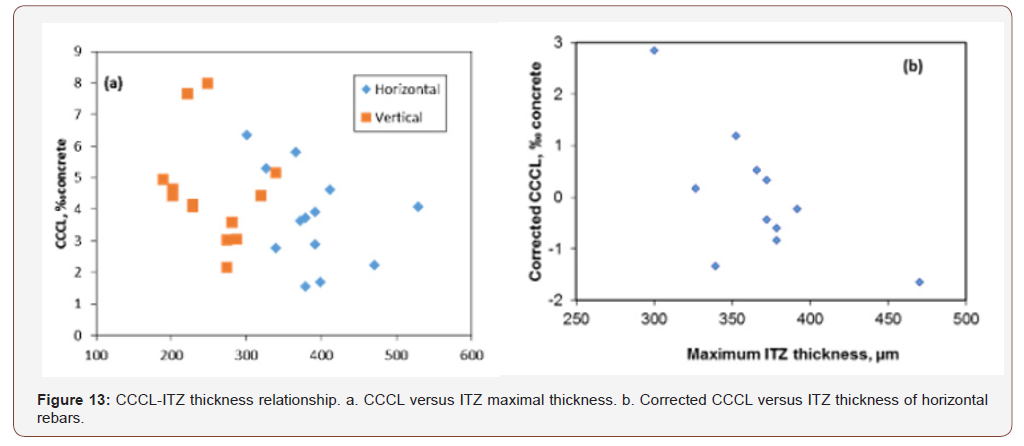
In addition to the correlation with steel-concrete distance, chloride threshold was also found to be correlated with ITZ thickness, for horizontal rebar orientation, especially with respect to its average value (Table 7 and Figure 13a).
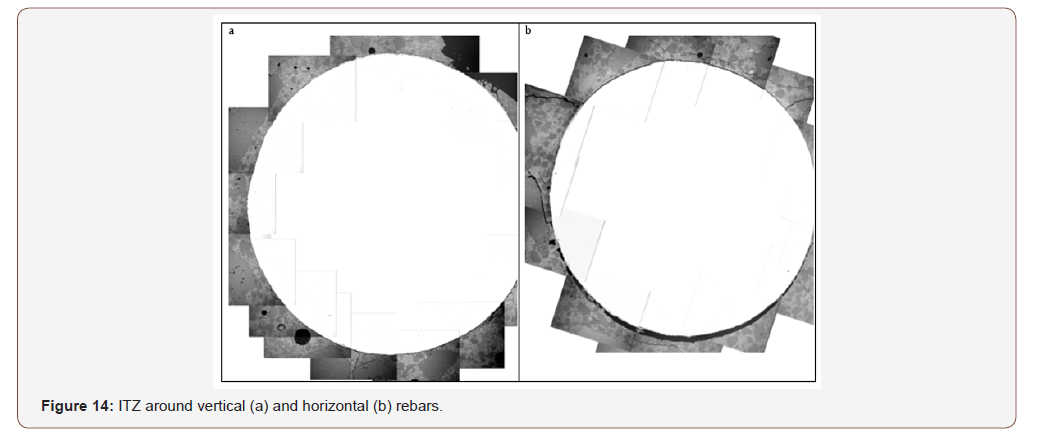
No significant correlation was found between chloride threshold and ITZ thickness for vertical rebars. The possibility that the good correlation identified for horizontal rebars is actually the result of inter-correlation between ITZ thickness and steel-concrete distance was examined. The correlation coefficient between ITZ thickness and steel-concrete distance was calculated and was found to be ~0.15, with a p-value of ~0.62, indicating that it is highly probable that the two are not correlated [39]. Hence, the correlation with ITZ thickness is a standalone correlation and not the result of interrelation between ITZ thickness and steelconcrete distance. To improve correlations with ITZ properties other than steel-concrete distance, a linear relationship between CCCL and steel-concrete distance was assumed following Figure 9. The threshold value for each steel-concrete distance was calculated and subtracted from the actual measurement, yielding the net correlation between CCCL and ITZ properties without the effect of steel-concrete distance. Figure 13b presents the net correlation between chloride threshold (without the influence of steelconcrete distance), and maximal ITZ thickness of horizontal rebar. Correlation value of -0.68 with a p-value of 0.02 was found (Table 8). The same calculation for vertical rebar yields a correlation coefficient of only -0.22 with a high p-value. No other significant correlations were found between the corrected CCCL and ITZ properties for either orientation. As before, good correlation was found between CCCL and w/c ratio and total bleeding for vertical rebars, but correlation with cement content was inverse, which again raises the question of accurate CCCL representation. If CCCL is indeed a fixed percentile of the cement content, then a direct relation with cement content is expected when CCCL is expressed as ‰ concrete, whereas an inverse relation was found indicating that the corrected CCCL decreases as cement content increases. The correlation between ITZ thickness and the chloride threshold for horizontal rebar only can be explained by the nature of the ITZ located below horizontal rebar. This ITZ is composed of one single void only (Figure 14). Hence, the ITZ thickness actually represents the distance of the bulk concrete from the steel. Close examination of the steel surface showed a thin layer of material adhered to the steel surface in the large pore located beneath the horizontal rebar [29]. This turns the problem into a two scale problem: a distance of a few microns from the steel to the nearest solid, which is in fact the thin layer, and a distance of several dozen to hundreds of microns from the steel to the bulk concrete, which is the ITZ thickness (Figure 13b,14) (Table 8).
Table 8: Correlations between corrected CCCL and ITZ and concrete parameters (correlations with p-value below 0.05 are emphasized).

In the absence of a thin layer, the maximum ITZ thickness around horizontal rebar represents the distance for diffusion from the pit opening to the pit bottom, buffered by concrete solids, as appears in the model described by Galvele [28]. According to this explanation, a clear correlation between ITZ thickness and chloride threshold is expected, if the void is saturated. The presence of a thin layer of solids in closer proximity to the steel surface and different degree of pore saturation can, however, obscure this correlation. The low, but significant correlation, may result from un uniform saturation rate of the pores during wetting and drying cycles, changing the physical conditions from the conditions in the model. This layer can have a lower pH buffering capacity than that of the bulk concrete, or a dissolution rate that is too low to retain the equilibrium pH. In both cases, the attained pH is lower. For example, using data from Table 9, we may calculate and see that the influence on the critical current density of a solid of pH 12 that is located 10 μm from the steel equals to that of other solid of pH 13 that is located 100 μm from the steel. Glass et al. [37] demonstrate different pH buffering capacities of the phases encountered in concrete. In their work, they titrated pulverized cement paste with acid, and measured the acid quantities needed for pH reduction. Every peak of acid consumption for pH reduction indicates a phase with a specific buffering capacity at this pH. A review of these results, for CEM I, reveals components with buffering capacities of pH 12.5 and 11.4 and another component with a buffering capacity that ranges from 10.6 to 10.8 (Table 9).
Table 9: Critical product of pit depth (x) and current density (i) for different pH values outside the pit.
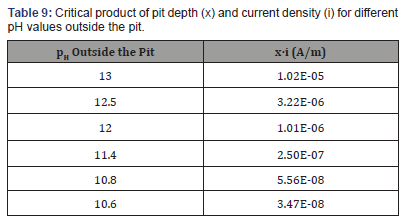
Figure 15 shows an example of the concentration polarization of hydroxide ions (pH) expected at the pit bases as a function of current density for two cases: i) a buffer of pH=12.5 located 146 mm from the steel surface; and ii) a buffer of pH=11.4 located 9.1 mm from the steel surface. These pH values correspond to the values reported in Glass et al. [37] for distances similar to the ones found in the current study. Figure 16 also reveals that the lines representing the concentration polarization are similar. Thus, due to variations in the chemical-physical environment of the actual concretesteel interface, the two effects may act simultaneously, indicating correlation with both properties (ITZ thickness and steel-concrete distance).
In the case of vertical rebars, the ITZ structure is different, exhibiting randomly varying thickness around the rebar rather than one single large void, as is found beneath the horizontal rebars. A two-scale effect can, therefore, explain the correlation with both ITZ thickness and steel-concrete distance in specimen with horizontal rebars, while in the case of vertical rebars, the only correlation observed is with steel-concrete distance. Researchers observed the different chemistry of the hydration products in the ITZ [40-43], which supports the assumption that various minerals precipitate on pore-paste and pore-steel interfaces, with a different pH value than other hydration products.
Conclusion
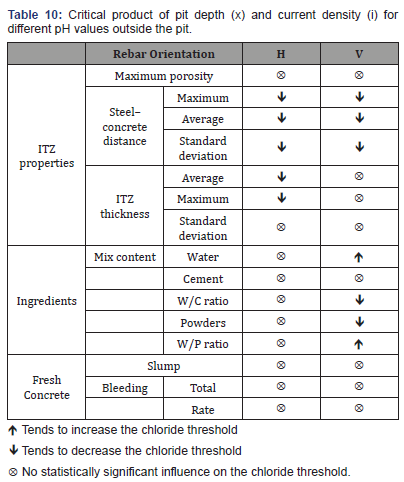
1. Statistical analysis was conducted to find correlations between CCCL and mix composition, fresh mix properties, and ITZ properties. Table 10 presents a summary of the influence of the tested parameters on the CCCL.
2. Chloride to concrete weight is the best representative form of the chloride threshold. The other methods examined (relative to cement content or [Cl-]/[OH-] in the pore solution) did not offer good representations of the threshold in actual concrete.
4. The model offered by Galvele [28] explains the above correlations when using the pH values of cement components and ITZ geometry found in the studied mixes. Concrete solids may have a different pH value and, according to the model, a change of one pH unit can change the calculated critical current density by an order of magnitude.
5. Deposits on the surface of the rebar may form a chemical environment that differs from the hydration product formed in the bulk concrete, farther from the rebar. Hence, two effects can be seen for horizontal rebar: the effect of deposits on the rebar (distance of a few microns) and the effect of the bulk concrete over a wide void (distance of ~100 mm and more). The second effect, however, may be irrelevant for most structures, because it may appear in saturated concrete only. The bulk concrete in specimens with vertical rebar is not separated by a clear void and so the effect of ITZ thickness is not as pronounced as in the case of horizontal rebars. The model presents high sensitivity to local pH values of the cementitious system surrounding the rebar. Therefore, different cement composition or using pozzolans may affect the chemical environment of the bulk concrete and of the deposits on the rebar, thus creating a different CCCL -ITZ relationships.
6. The variability of the microstructure chemical composition of the ITZ around reinforcing bars can explain the variation in the chloride thresholds found in laboratory and field research. It is clear that ideally, ITZ should be kept as small as possible. Yet, the techniques used to control the ITZ microstructure require further development in order to be useful in controlling the ITZ and to accurately determine the expected chloride threshold. They should start with a bullet. This is named conclusions.
Acknowledgement
Partial support by the Israel-Germany Foundation (GIF) grant number I–786-94.10 is gratefully acknowledged.
Conflicts of Interest
The authors and funding have no conflict of interests.
References
- Koch GH, Brongers MPH, Thompson NG, Virmani YP, Payer JH (2001) Corrosion Cost and Preventive Strategies in the United States.
- Pillai RG, Trejo D (2005) Surface condition effects on critical chloride threshold of steel reinforcement. ACI Mater J, pp.103-109.
- Schiessl P, Raupach M (1990) Influence of concrete composition and microclimate on the critical chloride content in concrete. In Proceedings of the Third International Symposium on Corrosion of Reinforcement in Concrete, p. 49.
- Luping T, Gulikers J (2007) On the mathematics of time-dependent apparent chloride diffusion coefficient in concrete. Cem Concr Res 37(4): 589-595.
- Medeiros MHF, Helene P (2009) Surface treatment of reinforced concrete in marine environment: Influence on chloride diffusion coefficient and capillary water absorption. Constr Build Mater.
- Oh BH, Jang SY (2007) Effects of material and environmental parameters on chloride penetration profiles in concrete structures. Cem Concr Res 37(1): 47-53.
- Song HW, Lee CH, Ann KY (2008) Factors influencing chloride transport in concrete structures exposed to marine environments. Cem Concr Compos 30(2): 113-121.
- Ehlen MA (2009) Life-365 Service Life Prediction Model and Computer Program for Predicting the Service Life and Life-Cycle Cost of Reinforced Concrete Exposed to Chlorides.
- Hussain SE, Rasheeduzzafar A, Al-Gahtani AS (1995) Factors affecting threshold chloride for reinforcement corrosion in concrete. Cem Concr Res 25(7): 1543-1555.
- Thomas M (1996) Chloride thresholds in marine concrete. Cem Concr Res 26(4): 513-519.
- Hope BB, Ip AKC (1987) Chloride Corrosion Threshold in Concrete. ACI Mater J 84(4): 306-314
- Oh BH, Jang SY, Shin YS () Experimental investigation of the threshold chloride concentration for corrosion initiation in reinforced concrete structures. Mag. Concr. Res 55(2): 117-124, 2003.
- Alonso C, Andrade C, Castellote M, Castro P (2000) Chloride threshold values to depassovate reinforcing bars embedded in a standardized OPC mortar. Cem Concr Res 30(7): 1047-1055.
- Alonso C, Castellote M, Andrade C (2002) Chloride threshold dependence of pitting potential of reinforcements. Electrochim Acta 47(21): 3469-3481.
- Kayyali OA, Haque MN (1995) The ratio of Cl$-$/OH$-$ in chloride contaminated concrete. A most important criterion. Mag Concr Res 47: 235-242.
- Ann KT, Song HW (2007) Chloride threshold level for corrosion of steel in concrete. Corros Scince 49(11): 4113-4133.
- Angst U, Vennesland Ø (2010) Critical chloride content in reinforced concrete-State of the art. in Concrete Repair, Rehabilitation and Retrofitting II.
- Cheewaket T, Jaturapitakkul C, Chalee W (2012) Initial corrosion presented by chloride threshold penetration of concrete up to 10 year-results under marine site. Constr Build Mater.
- Glass GK, Buenfeld NR (1997) The Presentation of the chloride level for corrosion of steel in concrete. Corros Sci 39(5): 1001-1013.
- Mohammed TU, Hamada H (2001) A discussion of the paper Chloride threshold values to depassivate reinforcing bars embedded in a standardized OPC mortar’ by Alonso C, Andrade C, Castellote M, Castro P. Cem Concr Res 31(5): 835-838.
- Zhang R, Xia Y, Xie L (2014) Effects of steel-concrete interface defects on corrosion cracking in chloride environment. in RQD 2014 - Proceedings - 20th ISSAT International Conference Reliability and Quality in Design.
- Uddin T, Otsuki N, Hisada M (1999) Corrosion of steel bars with respect to orientation in concrete. ACI Mater. J 96(2): 154-159.
- Mohammed TU, Otsuki N, Hamada H, Yamaji T (2002) Chloride-induced corrosion of steel bars in concrete with presence of gap at steel-concrete interface. ACI Mater J.
- Yu H, Shi X, Hartt WH, Lu B (2010) Laboratory investigation of reinforcement corrosion initiation and chloride threshold content for self-compacting concrete. Cem Concr Res 40(10): 1507-1516.
- Glass GK, Reddy B (2002) The Influence of the Steel Concrete Interface on the Risk of Chloride Induced Corrosion Initiation in COST 521, Final Workshop, Luxembourgh 18(19): 227-232.
- Glass GK, Yang R, Dickhaus T, and Buenfeld NR (2001) Backscattered electron imaging of the steel-concrete interface. Corros. Sci 43(4): 605-610.
- Horne T, Richardson IG, Brydson RMD (2007) Quantitative analysis of the microstructure of interfaces in steel reinforced concrete. Cem Concr Res 37(12): 1613-1623.
- Galvele JR (1976) Transport processes and the mechanism of pitting of metals. J Electrochem Soc 123(4): 464-474.
- Kenny, Katz A (2012) Characterization of the interfacial transition zone around steel rebar by means of the mean shift method. Mater. Struct. Constr 45(5).
- Kenny, Katz A (2015) Statistical relationship between mix properties and the interfacial transition zone around embedded rebar. Cem Concr Compos 60: 82-91.
- Taylor HFW (1987) A method for predicting alkazi ion concentrations in cement pore solutions. Adv Cem Res 1(1): 5-17.
- Ulloa VA, García-Taengua E, Pelufo MJ, Domingo A, Serna P (2013) New views on effect of recycled aggregates on concrete compressive strength. ACI Mater J 110(6): 687-696.
- Parsekian GA, Fonseca FS, Pinheiro GL, Camacho JS (2014) Properties of mortar using cubes, prism halves, and cylinder specimens. ACI Mater J 111(4): 443-454.
- Strauss A, Bergmeister K, Hoffmann S, Pukl R, Novák D (2008) Advanced Life-Cycle Analysis of Existing Concrete Bridges. J Mater Civ Eng.
- Yonezawa T, Ashworth V, Procter RPM (1988) Pore Solution Composition and Chloride Effects on The Corrosion of Steel in Concrete. Corrosion.
- Pourbaix M (1966) Atlas of Electrochemical Equilibria in Aqueous Solutions (2nd) Pergamon Press, Israel.
- Glass GK, Reddy B, Buenfeld NR (2000) Corrosion inhibition in concrete arising from its acid neutralisation capacity. Corros Sci 42: 1587-1598.
- Grubb JA, Hemant SL, Kakade AM (2007) Testing pH of Concrete, need for a standard procedure. Concr Int 29: 78-83.
- Kenny (2012) The microstructure of concrete around embedded steel influence on the chloride threshold for chloride induced corrosion. Technion - Israel Institute of Technology.
- Page L (2009) Initiation of chloride-induced corrosion of steel in concrete: role of the interfacial zone. Mater Corros 60(8): 586-592.
- Gallias L, Cabrillac R (1998) Action of chloride ions on the reactions in the corroded steel cement paste interfacial transition zone. in Proceeding of the international RILEM conference No. 35 The interfacial zone in cementitious composites pp.163-170.
- BelaId F, Arliguie G, François R (2001) Porous structure of the ITZ around galvanized and ordinary steel reinforcements. Cem Concr Res 31(11): 1561-1566.
- Gallias JL (1998) Microstructure of the interfacial transition zone around corroded reinforcement in the interfacial Transition Zone in Cementitious Composites. Pp.171-178.
-
Amit Kenny, Amnon Katz. Steel-Concrete Interface Influence on Chloride Threshold for Corrosion – Empirical Reinforcement to Theory. Cur Trends Civil & Struct Eng. 4(3): 2019. CTCSE.MS.ID.000586.
-
Concrete, Chloride threshold, Rebar, Corrosion, Interfacial transition zone, Back scattered electron microscopy, Water reducer, Reinforced concrete, Corrosion, Chloride
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






