Active Control of the Nonlinear Vibrations in Suspension Bridges due to Wind and Vertical Moving Loads

Long steel suspended cables such as those used in suspension bridges are prone to vibrations induced by wind and traffic moving loads. Suspended cables supporting bridge decks are tensioned due to their own weight, the weight of the bridge deck and the traffic loads. When the suspended cable is subjected to any disturbance due to wind or moving vertical loads, and because of the coupling between the motion of the bridge deck and the motion of the suspended cables, the system behaves nonlinearly due to the flexibility of the suspended cables. The nonlinear dynamic response affects the safety and serviceability of these flexible structures. Researchers have studied the nonlinear vibrations of a suspended cable due to wind or periodic excitations. Abdel- Rohman and Spencer [1] showed that introducing a small damping to the suspended cable improves tremendously its dynamic response. Passive control can provide, in some cases, a good control for the nonlinear vibrations response in the cable stayed bridges or suspension bridges [2-4]. Active control of flexible structures is a valuable new technology to enhance the flexible structures functionality and to ensure their safety. The control of the nonlinear vibrations response of the suspension and cablestayed bridges due to wind and/or traffic loading has attracted the interest of many researchers [5,6]. Because of the high cost of the active control technology, some attempts have been made to combine active and passive control, which is now called semiactive control [7,8]. Spencer & Nagarajaiah [9] reviewed the recent and rapid developments in the semi-active structural control and their implementation in full-scale structures. Benchmark control problems for cable-stayed bridges were studied [10]. The design of the active control actions can be achieved using the classical and modern control design methods [11]. A reliable active control system depends on using a feasible control mechanism and good design of the control actions to ensure the dynamic stability of the controlled structure.

In this paper, the responses of the nonlinear vibrations for the suspended cables and the suspension bridge deck due to wind and moving vertical loads are obtained. In order to introduce more damping to the bridge, two control mechanisms are proposed. The first control mechanism consists of a rigid vertical link or a pre-tensioned vertical cable connecting the bridge deck with the suspended cable by an electro-hydraulic actuator. The other control mechanism depend on using pre-tensioned cables and a rigid vertical link connected to the actuator to form a king-post truss [12]. The electro-hydraulic actuator response is designed to keep the controlled structure safe and serviceable at all times. The design of the actuator response utilizes the information received from the sensors, which are placed at specific locations on the bridge to measure the deflection, velocity and/or acceleration responses [11]. Since the design of the control forces for the nonlinear systems is more involved, this paper presents a simple design for the active control force to control the nonlinear dynamic response of the suspension bridges due to the wind and the moving vertical loads. The active control force is based on the velocity measurements taken at the control force location. The designed control force is first utilized on a linear structural model before applying it on the actual nonlinear structural model. Comparison between the controlled response using the suggested control mechanism and the uncontrolled response in addition to the assessment of the magnitude of the active control force will indicate the feasibility of the suggested control mechanism.

The basic equations of motion of the suspended cables are defined by Abdel-Rohman & Spencer [1], Irvine, 1992 [13] and Luongo & Piccardo [14]. According to the displacements directions defined in Figure 1, the general equations of the suspended cables motion are as follows:

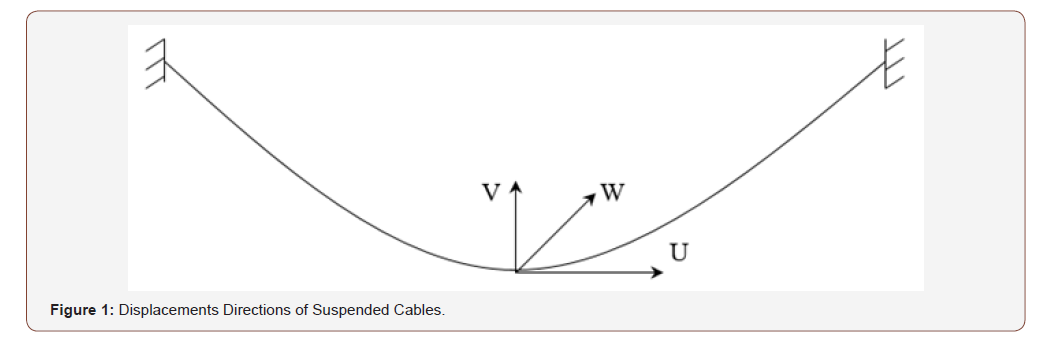
in which (s) is the spatial coordinate along the cable curved length. (t) is the time. (x) is the horizontal coordinate along the cable span. y(s) is the cable static profile. U(s, t), V(s, t) and W(s, t) are, respectively, the displacements in the tangential, vertical and transversal directions. (T0) is the static tension. (τ) is the additional dynamic tension in the cable. (c) is the damping coefficient. (m) is the mass of the cable per unit length. (g) is the acceleration of gravity. The applied loading per unit length in the vertical direction is fv(s, t) and in the transverse direction is fw(s, t). The nonlinear strain-displacement relationship during the deformation of the cable is given by:

where (E) is the modulus of elasticity and (A*) is the cross section area of the suspended cable.

The deformed cable segment (ds’) and the un-deformed cable segment (ds) are obtained from:

in which (x) and (y) are, respectively, the horizontal and vertical Cartesian dimensions.

A two-hinged bridge deck is supported by the suspended cables using vertical hangers located at (s = si) on the cable and at (x = xi) on the bridge deck. A control mechanism consists of a rigid vertical link or a pre-tensioned vertical cable connecting the bridge deck with the suspended cable using an electro-hydraulic actuator. The actuator is used to apply an active vertical control force u(t) at the mid-span of the bridge deck and at the mid-span of the suspended cables, as shown in Figure 2. The equations of motion for the suspension bridge model can be simplified based on the assumption of a small curvature regime and neglecting the tangential motion in the case of zero longitudinal loading to as follows:

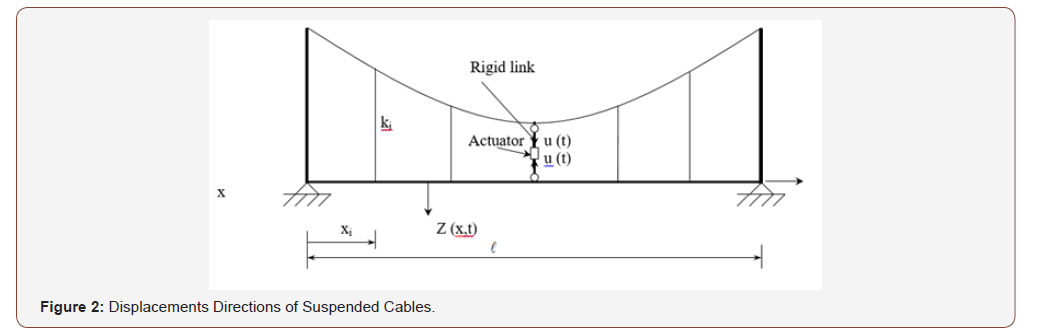
in which (EI) is the flexural rigidity of the bridge deck. (cb) and (mb) are, respectively, the damping and mass per unit length of the bridge deck. (P) is the magnitude of the vertical load which is assumed to be moving with a constant speed ( v ) and at any time (t) is located at (x = xp = vt ). (ki) is the stiffness of the vertical hanger (i) which is located at (x = xi) along the bridge deck of span and located at (s = si) along the suspended cable of span ( *). u(t) is the vertical concentrated active control force which is located at the mid-span, ( x = 0.5 ) and ( s = 0.5* ). Z(x, t) is the vertical response of the bridge deck.

The notations (Zi) and (Vi) indicate, respectively, the vertical deflection response of the bridge deck and the vertical deflection of the suspended cables at (x = xi) and (s = si). (δ) is the Dirac-delta function which is used to introduce the concentrated forces into the differential equations. The displacement functions W(s, t), V(s, t) and Z(x, t) are considered to be from the contribution of the first modes only. They are expressed as follows:

where λ (s) and φ (s)are, respectively, the first mode shape of the suspended cable in the transversal and vertical directions, which can be determined using the linear theory of cables to satisfy the boundary conditions [13]. For a hinged-hinged suspended cable, the first mode shapes for and which satisfy the boundary conditions are as follows:

For a simply supported bridge deck, the mode shape η(x) which satisfies the boundary conditions [Z(0, t) = 0 and Z = 0] is as follows:

Substituting equations (10) to (12) into equations (7) to (9) and applying an integral transformation, one obtains, respectively, the equations of motion of the suspended cable in the transverse direction, the vertical directions and the equation of motion of the bridge deck in the vertical direction as follows:

The aerodynamic forces on the suspended cables due to wind in the transverse direction can be estimated from the along-wind and across-wind forces Holmes [15] and Simiu & Scanlan [16] as follows:

where (ρ) is the air density, (D) is the cable diameter, (CD) is the drag coefficient, (CL) is the lift coefficient, (γ) is the angle of attack and (U_rel) is the relative wind speed with respect to the cable motion which is given by:

in which U (s, t) o is the mean wind speed, ( ) t , s W is the transverse velocity response of the cable in W-direction and ( ) t , s V is the vertical velocity response of the cable in V-direction.

From Figure 2, one obtains the following relationships:

The wind force functions and are usually obtained from the wind tunnel tests [17].

Curves that best fit the wind tunnel test data are used in the analysis. These functions can be expressed as polynomials in (tan γ) as follows:

where (N) is the degree of the polynomial, (ai) and (bi) are constants to be determined from the wind tunnel tests. Substituting equations (29) and (30) into equations (25) and (26), the expressions for F_w (t) and F_v (t) in equations (16) and (17) are determined from the integral transformations as follows:

Using equations (13), (14), (25) and (26) into equations (31) and (32), we obtain Fw(t) and Fv(t) in the following forms:

where the coefficients C_wi and C_vi are obtained from the equations shown in the appendix.

It is obvious from equations (33) and (34) the effect of the aerodynamic self-excited wind forces on the stability of the system. In order to determine the critical (onset) wind speed at which galloping starts for the bridge, one sets the determinant of the linear damping matrix equal to zero Abdel-Rohman & Spencer, [1] and Den Hartog [18] and solve for the critical wind speed from the following equation:

The design of the active control force u(t) can be obtained by several methods. The design method used here is to express u(t) as function of the output response of the system without the need to estimate the state variables of the higher order modes. Since the system is nonlinear, one can base the design on a linear system model. A linear system model can be obtained by ignoring the nonlinear terms because most of the civil engineering structures are usually weakly nonlinear. One can also linearize the nonlinear system around an equilibrium state. The linear system model considered for the sake of the design of the control force is defined as follows:

in which Fw*(t) and Fv*(t) contain the constant and the linear terms in Fw(t) and Fv(t) in equations (33) and (34). It is obvious from equation (36) that the linear time response L(t) in W- direction is uncontrollable due to locating the control force at the mid-span, which is the node of the mode shape λ(s). However, Abdel-Rohman and Spencer [1] have shown that the lateral response W(s, t) due to wind is very small as compared with the vertical response V (s, t). Therefore, the design of active the control force u(t) shall depend on the linear system defined only by equations (37) and (38) which can be expressed in a state matrix form as follows:

in which K is the general gain matrix of dimension (1×4).

The design of the elements of the gain matrix K requires the knowledge of the state variables (A, A ,B ,B ) , which represent the generalized coordinates of the first modes in V- and Z- directions. These state variables can be estimated using observers and filters and the design of the gain matrix K can be made by various methods such as the optimal control method or the pole-placement method [19]. The design method in this paper is based on the feedback of the measured velocity response at the same location of the control force [20]. The measured response shall include the contribution of all higher order modes. The design of the control force here depends on the assumption that the measured response are the contribution of the first modes only. In the case of using velocity feedback from velocity measurements collocated with the control forces locations, it has been proven by Balas [21] and was shown by Abdel-Rohman [22] that the higher order modes do not affect on the stability of the controlled linear system. The stability of a weakly nonlinear controlled system can be checked by studying the stability of a linearized system, which is obtained by perturbing the nonlinear controlled system about an equilibrium state [23].

The active control force is obtained from the following velocity feedback control law:

The gain factor (α) can be chosen to make the damping ratio of the first mode of the bridge deck reaches a certain value.

Numerical computations are made for an equivalent suspended cable (instead of two parallel suspended cables) of length ( * = 200 m), diameter (D =10 cm), mass (m =62 kg/m), tension in the cable (H = 2 × 106 N), axial stiffness (EA*= 1.57× 109 N), the damping ratio in the cable (ξ = 0.1%). The bridge deck parameters are: the span ( = 180 m), the mass (mb = 104 kg/m), the flexural rigidity (EI= 3.29×1010 N.m2), the damping ratio in the bridge deck is (ξ b = 0.01), the speed of the moving load is ( v = 27 m/sec). The active control force u(t) is applied at mid-span, ( x = 0.5 ) and at ( s = 0.5* ). The stiffness of the vertical hangers is assumed to be constant with (ki =107 N/m), and the spacing between the hangers is (10 meter) on the horizontal axis (i.e. x1 = 0, x2 = 10, x3 = 20, . . . to xN = 180 m). From these data, the natural frequencies for the cable and the bridge deck are determined from the expressions defined in the Appendix to be ( w ω ) = ( v ω ) = 2.8 r. p. s. and ( b ω ) = 0.552 r. p. s. The parameters defined in the appendix can then be calculated to obtain the following constants:

d₁ = 16163, d₂ = -16197, c_{1 = 1.2196, c2 = 0.41, c3 = 0.578, c4 = 0.565, c5 = 0.8015, c6 = 0.5634, c7 = 0.55, c8 = - 111.11, c9 =111.34, c10 = -1.11×10-6 and c11 = 0.00016129.}

For a moving load of (P = 9×104 N), the value of (P* = 0.10) and (Ω = 0.4712 r. p. s.).

The Uncontrolled Response

The uncontrolled response of the nonlinear system can be obtained from the numerical integration of equations (36) to (38) using the software (MATLAB) and considering the control force u(t) = 0 and assuming any assumed initial conditions. The uncontrolled response of the linear system model is obtained by solving equation (36) to (38) with neglecting the nonlinear terms in Fw(t) and Fv (t) and considering u(t) = 0 for the same assumed initial conditions. The initial condition for the displacement was considered equals (0.01 m) and for the velocity equals (0.01 m/sec). The response of the linear system model at the mid-span was found to be close from the response of the nonlinear system model, as shown in Figures 3 and 4.

The following performance indices were used to compare, the displacement responses of W(s, t), V(s, t) and Z(x, t) at the mid-span for the linear and nonlinear systems models:

The response indices for the uncontrolled linear system model are obtained for (T = 200 seconds) and compared with the response indices of the uncontrolled nonlinear system model as shown in Table 1. It is clear that the responses of the linear and nonlinear models are close to each other. One can then design the active control force for the linear system model and apply it to the nonlinear system model in order to obtain the controlled response of the nonlinear system model [24-28] (Table1).

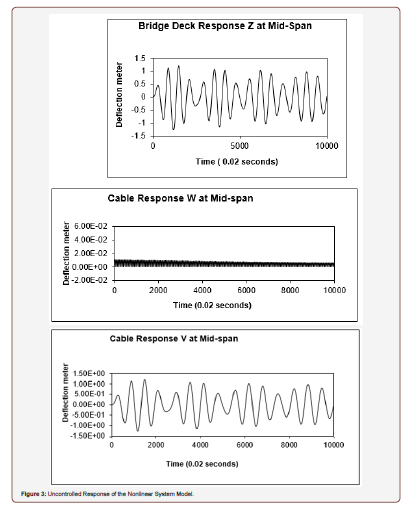
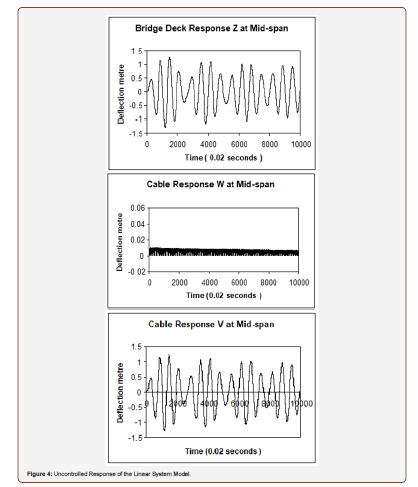
Table 1:Comparison of the Uncontrolled Response Indices for Time Period T = 200 seconds.

The controlled response using the proposed control mechanism (1)

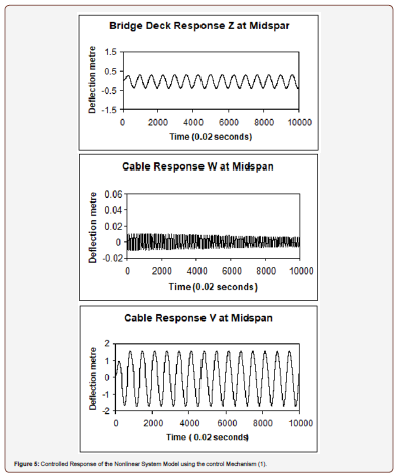
One may consider the control objective is to select a value for the gain factor (α) in equation (42) to make the damping ratio in the bridge deck equal certain value. For a damping ratio 90% and using equation (38), one determines the gain factor (α) to be (α = 109). Applying this control law to equations (36) to (38), the controlled responses of the nonlinear system model are obtained as shown in Figure 5. The increase in the cable vertical response, V(s, t), is due to the action of the active control force u(t) on the cable. Table 2 shows the comparison between the response indices of the uncontrolled nonlinear system and the controlled nonlinear system using the control mechanism (1). The response index for the bridge deck (JZ) was decreased by more than 80%, but the vertical response index for the cable (JV) has increased by more than 275%. The active control force response for the control mechanism (1) is shown in Figure 6. In order to have favorable controlled responses for both the bridge deck and the suspended cable, the control mechanism (2) of Figure 7 is considered. In this mechanism, the active control force is applied on the bridge deck alone and the coefficient (c11) becomes (c11= 0) and is taken out of equations (37) and (40) (Figures 5,6,7) (Tables 2,3).

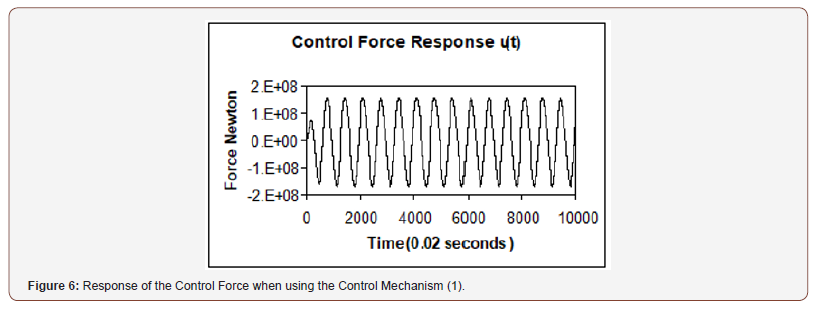
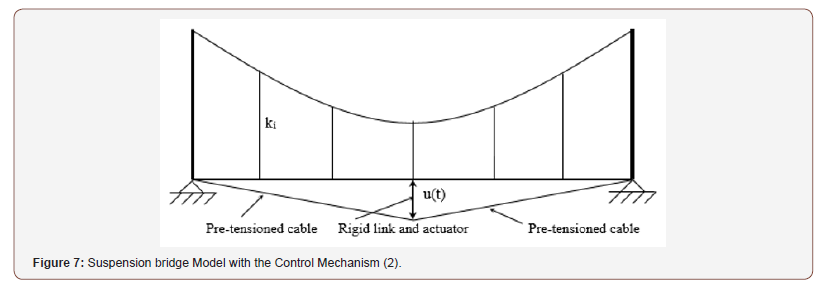
Table 2:Comparison of the Controlled and Uncontrolled Response Indices for Time Period T = 200 seconds and using the Control Mechanism (1).

Table 3:Comparison of the Controlled and Uncontrolled Response Indices for Time Period T = 200 seconds and using the Control Mechanism (2).

The control law for the control force u (t), is given by equation (42), where the gain factor (α = 0.58×106) is determined from equation (18) to have a damping ratio in the bridge deck equal (50%). The responses of the controlled nonlinear system model are obtained as shown in Figure 8 and the control force response is obtained as shown in Figure 9. Table 3 shows the comparison of the response indices, when using the control mechanism (2), with the uncontrolled nonlinear system response. It is shown that the response index for the bridge deck was decreased by more than 85% and the vertical response index for the suspended cable has decreased by more than 85% as compared with the response indices of the uncontrolled nonlinear response. To compare the magnitude of active control forces of the two proposed control mechanisms, the following control force index is used:

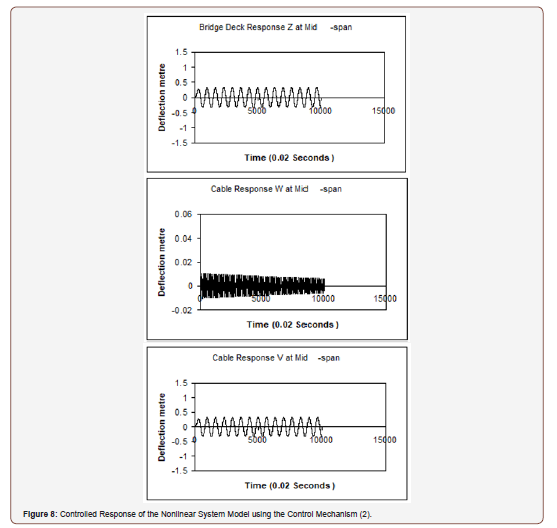
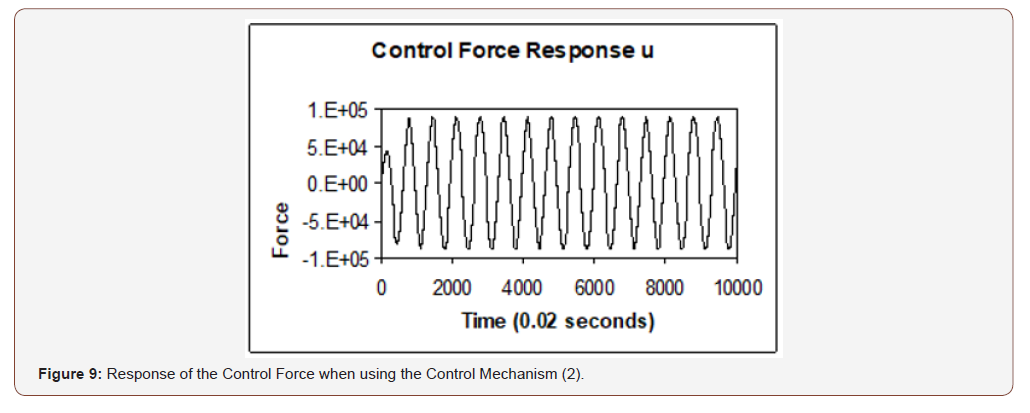
Table 2 shows that the active control force index for using the control mechanism (1) is (J_u=2.55×10¹⁸) and Table 3 shows the control force index when using the control mechanism (2) is (Ju = 7.64×1011). The consumption of the control energy for using the control mechanism (2) is too much smaller than that of using the control mechanism (1) (Figures 8,9).

The vertical responses of the cable and the bridge deck are shown in Figures 5 and 6 when using the control mechanism (1). The vertical responses of the cable and the bridge deck are shown in Figures 8 and 9 when using the control mechanism (2). The comparison indicates that the control mechanism (2) is more efficient than the control mechanism (1) and consumes smaller control energy. This indicates that the feasibility of the active control in the civil engineering structures depends mainly on the type of the control mechanism, not only on the design method of the control forces.

To control the suspension bridges nonlinear vibrations due to wind and vertical moving load, two control mechanisms were proposed. The control mechanism (1) consists of a rigid vertical link or a vertical pre-tensioned cable connecting the bridge deck with the suspended cable by an electro-hydraulic actuator at midspan. The control mechanism (2) consists of pre-tensioned cables and a rigid link at mid-span in the form of a king-post truss. The active control force is generated by an electro-hydraulic actuator, which is installed between the rigid link and the bridge deck. The design of the controller is based on the feedback of the velocity measurements taken at the control force location. The design of the active control force is first made on a linearized system model before applying it on the actual nonlinear system model. The gain factor parameter (α) is determined according to specifying a certain damping ratio for the controlled linear model. The design method for the active control force was used for the two proposed control mechanisms. It has been shown that the control mechanism (2) in which the reactions of the control force are supported by fixed platforms is very efficient as compared with the control mechanism (1) in which the reaction of the control force is supported by the suspended cables. This indicates that the feasibility of the active control in the civil engineering structures depends mainly on the type of the control mechanism, not only on the design method for the active control forces.

The Research Administration of Kuwait University under grant number EV01/05 has funded the Research in this paper.

No conflict of interest.

1. Abdel-Rohman M, Spencer BF (2004) Control of Wind-Induced Nonlinear Oscillations in Suspended Cables. Nonlinear Dynamics 37 (4): 341-355.
2. Abdel-Rohman M, Askar H (1996) Control by Passive TMD of Wind-Induced Vibrations in Cable Stayed Bridges by Tendons. Journal of Vibration and Control 2: 251-267.
3. Chang CC, Gu M, Tang KH (2003) Tuned Mass Dampers for Dual-Mode Buffeting Control of Bridges. J. Bridge Engineering 8(4): 237-240.
4. Soong TT, Spencer BF (2002) Supplemental energy dissipation: state – of – the – art and state – of – the practice, Engineering Structures, 24: 243–259.
5. Abdel-Rohman M, Askar H (1994) Active Control of Nonlinear Vibrations in Cable Stayed Bridges by Tendons, Journal of Kuwait University, Science 21: 153-166.
6. Huynh T, Thoft-Christensen P (2001) Suspension Bridge Flutter for Girders with Separate Control Flaps. Journal of Bridge Engineering, ASCE 6 (3): 168-175.
7. Agrawal AK, Yang JN, He WL (2003) Applications of Some Semi-active Control Systems to Benchmark Cable-Stayed Bridge. Journal of Structural Engineering 129(7): 884-894.
8. Johnson EA, Christenson RE, Spencer BF (2003) Semi-active Damping of Cables with Sag. Computer-Aided Civil and Infrastructure Engineering 18(2): 132-146.
9. Spencer BF, Nagarajaiah S (2003) State of the Art of Structural Control, J. Structural Engineering 129(7): 845-856.
10. Dyke SJ, Caicedo JM, Tauran G, Bergman LA, Hague S (2003) Phase-I: Benchmark Control Problem for Seismic Response of Cable-Stayed Bridges. Journal of Structural Engineering: Special Issue on Semi-Active Control 129 (7).
11. Leipholz HH, Abdel-Rohman M (1986) Control of Structures, Martinus Nijhoff Publishers, Boston.
12. Abdel-Rohman M, Nayfeh AH (1987) Active Control of Nonlinear Oscillations in Bridges. Journal of Engineering Mechanics, ASCE 113: 335-348.
13. Irvine M (1992) Cable Structures, Dover Publications, Inc, New York, USA.
14. Luongo A, Piccardo G (1998) Non-Linear Galloping of Sagged Cables in 1:2 Internal Resonance, Journal of Sound and Vibration, 214(5): 915-940.
15. Holmes JD (2015, wind loading of structures, CRC Press.
16. Simiu E, Scanlan RH (1996) Wind effect on structures: Fundamentals and applications to design, John Wiley & Sons, New York, USA.
17. Korlin R, Starossek U (2007) Wind tunnel test of an active mass damper for bridge decks. Journal of Wind Engineering and Industrial Aerodynamics 95 (4): 267-277.
18. Den Hartog JP (1985) Mechanical Vibrations, Dover Publications.
19. Abdel-Rohman M, Leipholz HH (1978) Structural Control by the Pole Assignment Method. Journal of Engineering Mechanics, ASCE, pp. 1159-1175.
20. Abdel-Rohman M (2005) Design of a Simple Controller to Control the Suspension Bridge Nonlinear Vibrations due to Moving Loads. Journal of Vibrations and Control 11(7): 867-885.
21. Balas MJ (1979) Direct Velocity Feedback Control of Large Space Structures. Journal of Guidance, Control and Dynamics pp. 252-253.
22. Abdel-Rohman M (1986) Active Control of Distributed Parameters Structures by Point-wise Control Actions, Proceedings of the Third conference, Dynamic Response of Structures, Engineering Mechanics Specialty Conference, ASCE, Los Angeles, pp. 756-763.
23. Nayfeh AH, Mook DT (1979) Nonlinear Oscillations, John Wiley.
24. Abdel-Rohman M, John MJ, Hassan MF (2010) Compensation of time delay effect in semi-active controlled suspension bridges. Journal of Vibration and Control 16 (3).
25. Abdel-Rohman M, John MJ (2006) Control of wind induced non-linear oscillations in suspension bridges using Multiple Semi-active tuned mass dampers. Journal of Vibrations and Control 12 (9): 1011-1046.
26. Abdel-Rohman M, John MJ (2006) Control of wind induced non-linear oscillations in suspension bridges using a Semi-active tuned mass dampers. Journal of Vibrations and Control 12 (10): 1049-1080.
27. Almutairi NB, Zribi M, Abdel-Rohman M (2011) Lyapunov-Based control for suppression of wind-induced galloping in suspension bridges. Mathematical problems in Engineering.
28. Murphy TP, Collins KR (2004) Retrofitting Suspension Bridges Using Distributed Dampers. J. Structural Engineering, 130 (10): 1466-1474.