Achieving A Higher Optimality for Lattice Steel Structures Utilizing A Multi-Layer Optimization Scheme

Research studies offer several tools that aim to improve the design of structures in order to achieve a safe and economic design. However, such tools are not always manipulated to be used in practical design applications. Structural optimization is one of the tools that have proven to have a noticeable impact on various aspect of the construction and design process [1]. Steel is extensively used as a construction material in many projects due to its superior mechanical properties, and its structural performance [1]. However, it is more costly when compared to other building materials (e.g. concrete, wood, etc.). The effectiveness of the material design becomes more evident in large scale projects due to its economic and environmental impact. According to the current urbanization and consumption rates of the world resources, serious actions need to be taken to enforce and ensure the sustainability of the resources. In many countries, effective decisions are already being taken to limit the greenhouse gases (GHG) emission and limit the damage that had already occurred to the environment [2]. The world is now taking a direction to design buildings and structures that are more energy efficient. However, there are ways to reduce this environmental footprint. For example, reducing the energy coming from making new materials in the first place, either by using recycled materials, or reducing the needed materials for new projects [2]. Therefore, tools like optimization became inevitable in the construction process. In order for the optimization process to reach that target, many variables and objective functions can be set for the optimization process. Examples of these parameters can be minimizing weight, increasing stiffness, or decreasing buckling length. However, the existence of constraints is extremely important to govern the solution of the optimization process [3]. Due to the advancement of computational capabilities, computationally expensive iterative approaches became more practical and tempting as it guarantees and optimized solution [3]. There are many types of optimization methods, like the mathematical design method, or the iterative-intuitive method [4]. The two methods are conceptually different, where in the mathematical optimization method, the searching algorithm is guided by a set of mathematical formulation, which unlike intuitive random search method can reach the solution in shorter time. However, there are several conditions that must be satisfied to use mathematical based design problems efficiently. There are several categories for structural optimization such as layout optimization, topology optimization, shape optimization, and size optimization. This study is concerned with topology optimization and size optimization. Topology optimization aims to find the optimum material distribution for a given domain, while size optimization objective is to minimize the weight of the elements used in the selected topology. Topology optimization is motivated by the theory presented by James Clerk Maxwell in the 1870 which states that the summation of all the structure’s tension load path minus the summation of the compression load path is equal to a constant value that is related to all the external forces applied on the system, including the reactions [5], this value will be referred within the scope of this research as “load path”. This theory had been modified over the years and the field of topology optimization advanced significantly to cover various application such as structural design, acoustic design [6], thermal manipulation within structural elements [7]. On the other hand, the size optimization is concerned with minimizing or maximizing one or more of the model characteristics such as the member weight. size, buckling load, vibration properties, embodied energy, etc. This objective is achieved through searching for the optimum values of the given variables while satisfying a set of predefined constraints.

The aim of this study is to highlight the literature proposing two-layered optimization framework that bridges the gap between the research and the practical industry. The proposed framework is applied to two case studies to evaluate its effectiveness in reducing the cost of the structure. Additionally, a parametric study is performed to determine the relationship between the span of a bridge and the height of the structural system. Over the past years several researchers worked on the development of the topology optimization problem. Several of their studies aimed to make the problem more practical. For instance, Rosyid and Caldwell in 1991 [8] proposed a design approach based on layout of structural systems that is a less software intensive as an alternate method to ground structures and homogenization approaches. The approach proposed utilize two- design methods implementation based on cognitive modeling. The determination of the topology of the structure prior to the design stage would increase the efficiency of the structure in resisting the applied loads and save much of the construction material, which in turn would decrease the environmental footprint of the structure. This research shed light on the importance of improving the methods used in the generation process of the topology of the structure, as Mijar et al. explored [9]. In their paper “Continuum Topology Optimization for Concept Design of Frame Bracing Systems”, they started exploring a new methodology other than the discrete ground structure topology optimization methods, which is a Continuum structural topology optimization formulation. In the tall buildings, the stiffness of the overall structure is very important, not only to the serviceability limit state, but also to accommodate for the cladding and light walls or the glass panels. At this point, the determination of the layout of the structure that would achieve the optimal response is of high importance. This paper tackles the continuum topology optimization problem using the Voigt and Reuss rules for materials’ mixing. The formulation of such a problem is an extremely general process that can be utilized for designs involving both, elastic and inelastic materials [10]. However, the study in discussion deals with elastic materials. The study showed that the topology-optimized systems considerably improved the performance of the structure in case of the compliance, displacements, and vibrational frequencies. The Authors utilized the continuation solution to take advantage of the properties of the Pure Voigt and Reuss formulations [9].

As a continuation of the attention given to the selection of continuum structures subjected to displacement constraints, in 1999 Liang et al. [11]started exploring ways to achieve the optimum topology by generating a technique that eliminates underutilized element from the discretized domain of the structure. In the following phase, the element elimination criteria were derived by conducting a sensitivity analysis on the structure due to the removal of elements that are underutilized. The paper concluded that the performancebased optimization approach can be effectively utilized to generate the optimal structural topologies. The paper also reached the conclusion that smoother solutions can be reached by using smaller element elimination ratios in the performance optimization process, but the authors had to increase the computational cost to achieve that [12]. The advancement in topology optimization included the determination of the optimal topology as well of the bracing system for a steel multistory building subjected to numerous lateral loading cases, whereas the constraint is the overall stiffness [12]. Afterwards, several studies focused on developing various optimization approaches to suite different applications [13,14]. In 2007, Robert Baldock explored 3 different optimization methods applied to bracing lateral resisting systems. The optimization problem is further enhanced to incorporate the aesthetic appeal while satisfying the stiffness and economy requirements [15,16]. Lauren et al. 2011 extended the optimization problem using the concept of pattern repetition (Pattern Gradation) [17]. This approach repeats geometrical patterns in the building, which makes it possible to generate optimal patterns for the lateral bracing systems with the most optimized inclination angles. They also introduce manufacturing constraints to the optimization process, while also focusing on the pattern gradation constraints [18]. Zhen John Goo in 2013 tried another approach to determine the optimum topology of the bracing for structural steel frames but using a different approach than his predecessors. His work depended heavily on linking the optimization program with the analysis program, so that the optimization loop would be automatically adjusting itself with each iteration with the results coming out from the analysis of the previous iteration. The study concludes that the steel frame structure designed utilizing the proposed scheme in this study have proved to be more economical than the conventional steel frame structures [19,20]. This study aims to build upon the research efforts done in literature and take it a step forward to serve the practical purposes of the structural design. Where the outcome of the topology optimization problem is utilized, and another layer of optimization is applied to determine the minimum weight of each element of the system. The determined elements design is governed by the building code provisions, and hence, can be adopted in practical applications.

In this study, a framework is developed to find the most optimum design of lattice steel structures, both in configuration of members, and in the size of those members as illustrated in Figure 1. A multi-layer optimization scheme has been developed where the first layer uses topology optimization to get the most optimum orientation of the structural members to achieve minimum compliance which is the minimum deflection given a certain volume of material [21]. After the first optimization layer is concluded, a finite element model is developed using the layout proposed in the topology optimization layer, and the straining actions of all the members are determined. A second optimization layer commences using Interior Point Method, this optimization loop finds the most optimum cross sections to achieve both: Stress constraints, and serviceability constraints. The topology optimization problem is formulated as a material distribution problem that is trying to achieve the minimum compliance. Considering the structural or mechanical element to be occupying a design domain, referred to as Ωmat. The design domain is considered to be a subset of a reference domain, referred to as Ω, where it is deliberately chosen to allow for the definition of the loading condition, and the support condition [4,22,23] (Figure 1).

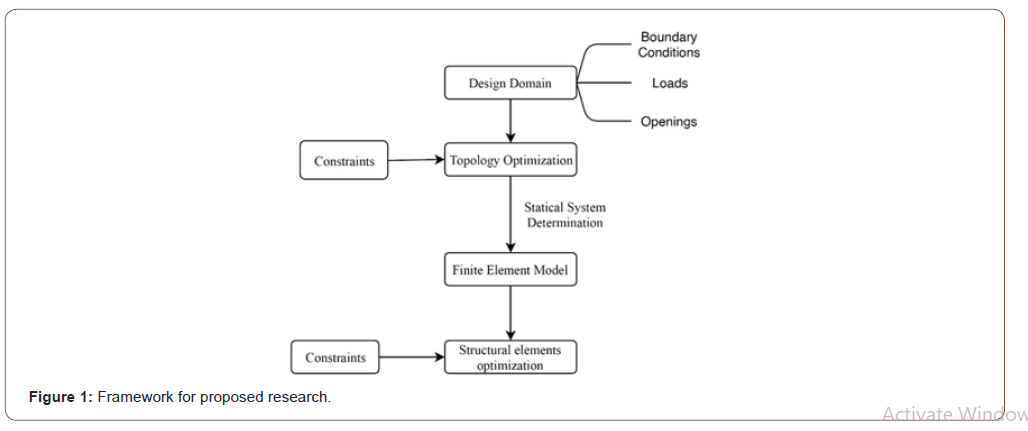
The problem definition can be stated as the problem of finding the most optimum stiffness tensor E_ijkl(x) which is set to be a variable over the design domain, and its notations are consistent with a Cartesian frame of reference which preserves its generality [24]. These finite elements forming the design domain follow a “Density- based approach”. In the Solid Isotropic Material with Penalization method (SIMP) the penalization factor is a value that is assigned on the material density. The density represents the isotropic material’s properties. The density interpolates between 0 and the E⁰_ijkl, where: 𝐸 E _ijkl (𝜌 = 0 ) = 0 and E_ijkl (𝜌 = 1 ) = E 0 ijkl. In turn, this would mean that if the final design had zero density, the pixel is considered as a void, and if it had a density of one, it’s a material. That would make the design domain like a checkered black/white board [24]. Thus, by specifying a penalization value over the density function, the value of this penalization factor needs to be relatively big to allow for true “0-1” solutions [16]. The mathematical form of the optimization Problem is constructed as follows:

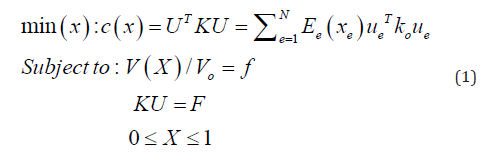
Where: c(x): Compliance over the design domain, U: Global displacement vector, F: Global Force Vector, K: Global stiffness matrix, u_e: Element displacement vector, k_o: Element stiffness matrix, N: Number of elements used in the discrete design domain, f: The volume fraction for the design problem, V(x): Material volume, V_o: Design domain’s volume. Where the sensitivities of the compliance c, and the material volume V with respect to the element densities x_e are:

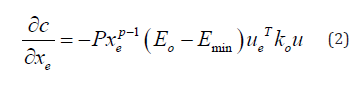
Where 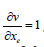To implement the topology optimization formulation, a powerful computational tool is required. MATLAB software is used for the algorithm formulation, which is an efficient platform for vector and matrix operations [25]. For the topology optimization application, the algorithm developed by Ole Sigmund in 2010 was sufficient for the applications presented in this research [21,23]. It is noteworthy that for advanced applications the same procedure can be followed; however, a new algorithm needs to be developed. For instance, some applications require the analysis of buckling problems, dynamic problems or even three-dimensional formalization. The design domain introduced in the formulation of the problem is set to be rectangular, and discretized by finite elements, square in shape, acting as pixels for the domain. After achieving the optimum topology according to the given domain, forces and boundary conditions, the user applies the outcome topology to finite element software to determine the straining actions on each element. Then another layer of optimization concerned with profile sizing is applied. There are numerous optimization models and techniques in the literature, in the scope of this research, interior point method is adopted for its ease of application and compatibility with goal of this research, which is demonstration of the proposed framework. Gradient Based method optimization methods (GBM) (e.g. interior point method) is optimum for problems with large number of variables, and it self-corrects by providing a way to search for a better direction after each iteration/step within the optimization scheme [3], where the design variable is updated at each loop as follows:

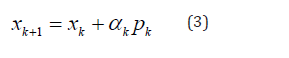
Where 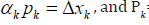Search direction, k=iteration number, 𝛼_𝑘=length of Step. The different types of Gradient-based optimization are different in the way they used to compute the search direction. The gradient of a function is presented as a vector of the partial derivative by the different variables, and that vector is perpendicular on the tangent plane on the surface of the boundaries.

For this step, an optimization code was developed that designs all the members as beam-column rectangular sections according to the American provisions AISC. The members were chosen to be rectangular hollow sections due to its ability to have high inertia in either direction, while having a lesser weight.

To demonstrate the applicability of the proposed research, two case studies were conducted to compare traditional structural systems to ones resulting from the proposed herein. For the case studies, two landmark structural systems were chosen, the first one is inspired from a Steel bridge over Ohio river in Pennsylvania, while the second structure is inspired by the structural system of the Hancock Tower in Chicago.

Case Study I

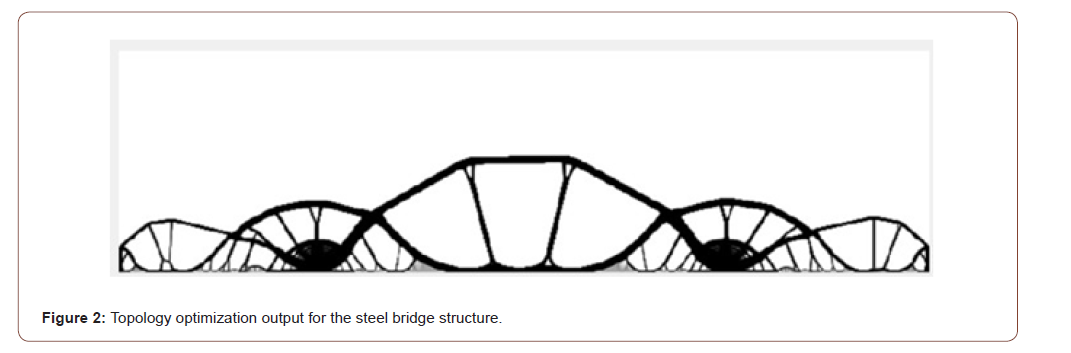
The bridge is Steel Cantilever through truss, with the main span equals to 724 ft (220 meters) the height of the main pier above deck is 35 meters [26-32]. In order to evaluate the efficiency of the proposed optimization framework, some assumptions were adopted in the analysis. The System was assumed to be designed for gravity loads only, with the model made for a two-dimensional analysis. The loads were calculated in accordance with the American Standards ASCE and the Egyptian Code for Load Calculations. In addition, to have a fair comparison for both systems, the members’ cross-sections for the benchmark problem, as well as the members’ cross-sections for the alternatives presented in this research were designed as rectangular hollow sections; this assumption ensures the high stiffness for cross section while maintaining the area to the needed amount only. Rectangular sections have high moment of inertia in both directions, resist lateral torsional buckling, and the area is highly sensitive to change in the thickness, which is very effective when designing for axial loads. The design procedure was made using the American Institute of Steel Construction standards (ASIC) while designing all the members to resist axial loads, and moments if needed, given that most of the structures are lattice structures, and the joints are released from moment restraints. Figure 2 shows the result of the first loop of the optimization process for proposing the structural system (Figure 2).

For the finite element Modeling, the loads were calculated in accordance with the Egyptian code for loads Calculation ECP201, 2012. Figure 3 shows the Finite element model for the Sewickley bridge, as built, and figure 4 shows the topology optimization output for the same domain and end conditions. As stated in earlier sections, the load path is considered an indication to the total energy stored within a structure, which is the total tension load path added to the total compression load path. The resulting magnitude is directly proportional with the deflection of the total structure, could be a resemblance to the design of the structure without taking the buckling into consideration. (Baker, 2012) In the Finite-element Model, the output was taken, and multiplied the Absolute value of the axial force in each member with its length, then calculated the summation of all the values (Figure 3).

After assigning all the sections in the model, the own weight and the maximum deflection are shown in Table 1, where the maximum deflection at the middle of the main span of the Sewickley bridge’s Model due to the all the applied loads and the own weight (Figure 4).

It was evident after completing the first cycle of design that the system that the difference in the weight between both systems was just 10%, where the As-built Sewickley bridge was heavier, while the load path was 63% more in the Sewickley bridge, that would indicate that the deflection in the Sewickley bridge model is much higher than that of the output inspired from the proposed optimization framework. That turned out to be true as the deflection of the Sewickley bridge is almost double that of the system inspired from the optimization framework. To have a closer to reality comparison, both systems would be adjusted to have a similar deflection, which is the allowable deflection. per the design codes, the value of the allowable deflection is not clearly stated, so the value was set to be (Span/450) which is about 50 cm. A new iteration was made, and all the members of the Sewickley bridge were designed with a lesser value of the stress ratio (Table 1).

As it can be observed, table 1 and the chart in figure 5(a), that in the first optimization cycle the weight of the original bridge, the Sewickley bridge, was 9.6% more than the weight of the system coming from the optimization framework. However, the deflection was almost 94.2% more than that of the optimization framework, while the Load path; which is the energy stored within the structure, was 63.1% more in the Original system than the Topology optimization output, which means that for the same volume (or weight) of materials, the deflection in the Sewickley bridge’s system should be more than that of the output of the topology optimization. Hence, the results in table 2 and figure 5(b) show the updated models (Figure 5a,5b and Table 2).

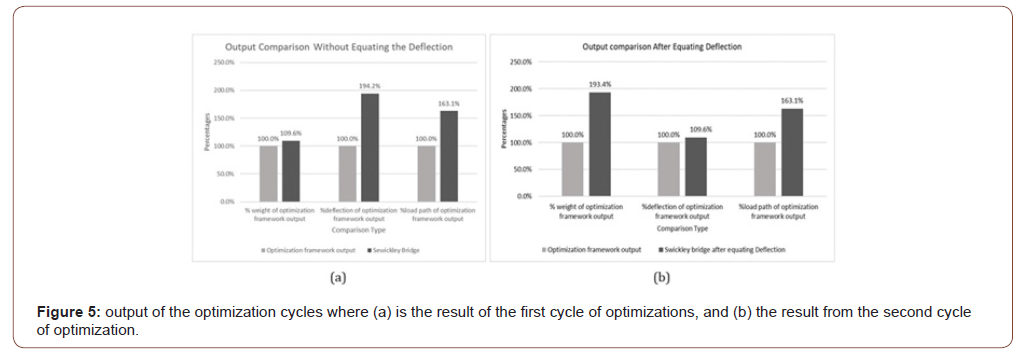
Table1:Comparison of output without Equating the deflection.

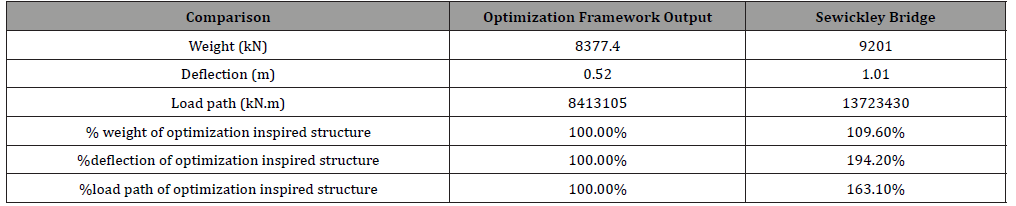
Table 2:Comparison of the output after Equating the deflection.

In the second cycle, the weight of the Sewickley bridge increased, increasing the difference in the weight from 9.6% to 93.4%, and the difference in the deflection almost diminished. The Load path is still the same given that the orientation of the members within the design domain did not change throughout the optimization scheme. The previous analysis confirms that the utilization of the optimization scheme has proved to be very important in reducing the environmental footprint of the structure and the overall weight, hence the cost, of the building materials, as reducing almost half of the materials, would reduce from the cost of the structural steel, and as previously mentioned, it is considered to be a total reduction in the overall cost of the structure.

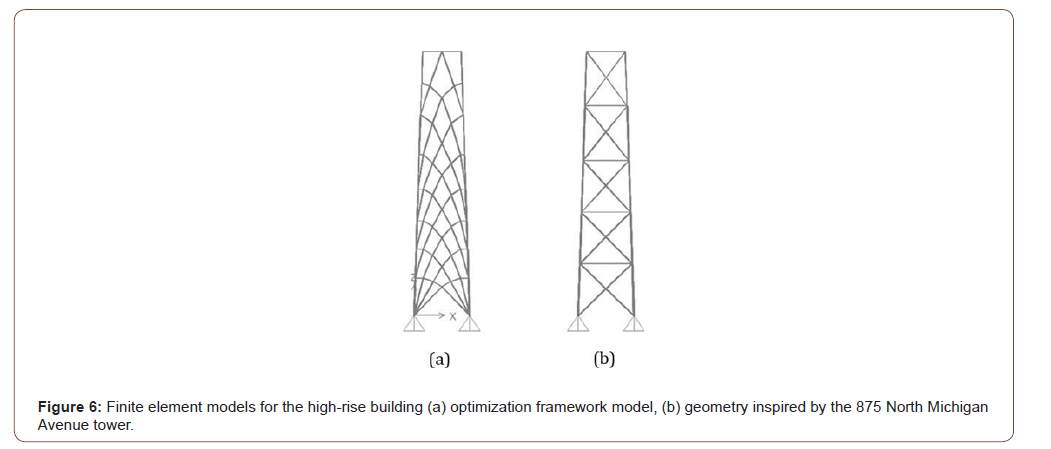
Case Study II: High-rise building

For this research purpose, the bracing System was assumed to be designed for lateral loads only, with the model made for a two-dimensional analysis. The wind loads were calculated in accordance with the ASCE-07, and the layout is inspired by the tower in 875 North Michigan Avenue, formerly the John Hancock Center [7], and it will be referred to herein as the “as-built tower”. The design procedure was conducted using the American institute of Steel Construction standards (ASIC) while designing all the members to resist axial loads, and moments where present, given that most of the structures are lattice structures that do not sustain moments. The topology optimization process for this tower was made through multiple iterations, and combining shapes coming from different underlying assumptions made regarding the connectivity of the skeleton bracing with the rest of the building, and whether the floors were part of the lateral force resisting system or not. As shown in figure 6, the shape of the lateral resisting system changes as the aspect ratio of the building changes, and the members take the form of stream lines to carry the loads safely from their point of action till the ground [12]. It was noted that the density of the members’ increase as we go downwards since the transmitted loads increase as the members intersect on their way to the support (Figure 6a,6b).

Using the same assumptions made for the previous case study, the loads were calculated in accordance with ASCE-07. The analysis is made on 2D analysis on wind loads calculated on the building per one side. The wind loads are calculated as they change with the height, and as the height increases, the surface area decreases due to the tapering, hence, the load (as pressure) per meter squared was multiplied by the width of the building at each point, and then, the resulting distributed load was multiplied by the distance between the joints of the lateral loads resisting system. After comparing the output from the first cycle of design, some observations were made that guided the direction of the following steps. In the first iteration, the weight of the as-built tower was higher than that of the proposed optimization framework tower, however the difference in the load path wasn’t as much as the weight, and that was due to the fact that most of the members of the as-built tower have a very high buckling length. The increase of the buckling lengths of the members lead to the increase of the overall weight of the structure. As the buckling length increases, the section gets bigger to accommodate that with larger inertia and dimensions, and as the depth and width of the section increases, the thickness needs to increase as well to avoid the possibility of local buckling within the section. As such, the comparison given all these factors would be unfair. A new approach is taken to overcome this shortcoming. In the design of the optimization framework case, the target stress ratio in the optimization process for all the sections was gradually decreased. Where in each iteration the decreased stress ration would give bigger sections than needed, and in turn it produces more inertia and reduce the deflection, till reaching the same deflection as the asbuilt tower in the design. As we can see in tables 3 and 4, and figure 7, that in the first cycle, the weight of the Original Tower (as- built tower) system was 62.5% more than the weight of the system coming from the optimization framework. However, the deflection was almost 34% less than that of the optimization framework inspired system. The load path was 6% more in the original system than the Topology optimization output (Table 3, 4 and Figure 7).

Table 3:Output of the first cycle without equating the deflection.

Table 4:Output of the second cycle after equating the deflection.

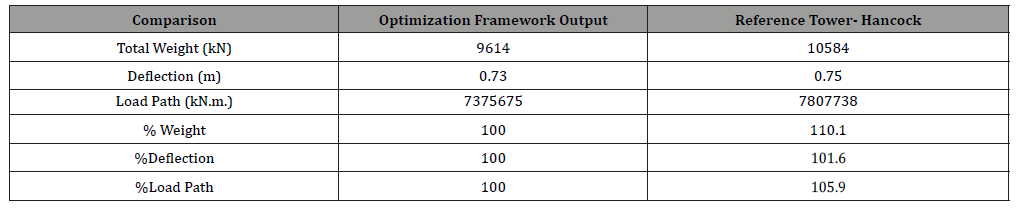
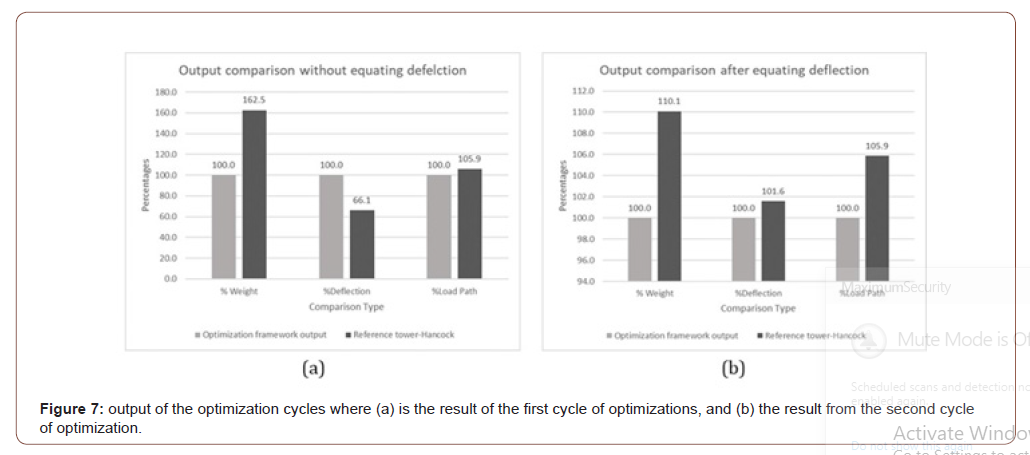
In the second cycle, the weight of the topology optimization model increased, reducing the difference in the weight from 62.5% to only 10.1%, and the difference in the deflection almost diminished to a mere 1%, while the Load path is still the same given that the orientation of the members within the design domain didn’t change throughout the optimization scheme. The previous analysis confirms that the utilization of the optimization scheme has proved to be efficient in reducing the environmental footprint of the structure and the overall weight, hence the cost, of the building materials, as reducing 10% from the cost of the structural steel is considered to be a total reduction in the overall cost of the building as mentioned in the first chapter. Nevertheless, the difference between the two system is close and hence, other factors such as aesthetics and ease of construction should be taken into account for the decision maker. The care given in the research community to incorporating the optimization in the initial concept design phase of any structure have proven to be important for future urban development, as the aforementioned loop confirms that a simple change on the orientation of the members within the domain of the structure can be of great impact on the design and behavior of the entire structure.

In this research, a framework of structural optimization has been addressed. This framework addresses two characteristics of the structural design elements in order to achieve certain objectives, like minimizing the overall weight of the structure. The first step is finding the most optimum topology of the structure within the design domain, using the Solid Isotropic Material with Penalization method. The second step is size optimization, where this step is made using interior point method optimization. The first optimization loop generates a layout for the structure, a finite element model of this structure is constructed based on the output of the topology optimization. After the analysis from the finite element model, the members are optimized using the interior point method optimization to a find the most optimum cross-section possible. In order to evaluate the proposed framework, two case studies were conducted, where two benchmark structures were considered, constructing a model of the as-built system, as well as a model from the output of the optimization scheme. The models are compared with one another in terms of load path, total deflection, and overall weight of the structure. The outcome of both case studies showed that the newly proposed layout

from the output of the optimization framework, resulted in a considerable decrease in the overall weight. The structure’s weight is less than that of the benchmark structure when equating the deflections of both structures with the allowable deflection. The study also showed that the load path was less in the newly proposed layout, which means that the total energy stored in the building is less. The proposed framework can be utilized as a tool for structural design engineers in the industry to develop more efficient and optimized structures, starting from a very early stage in any project, which is the layout stage.

None.

On behalf of all the authors, the corresponding author states that there is no conflict of interest.

1. Cormac Mc, Jack C, Stephen F, Csernak, Manojkumar, et al. (2011) structural steel design. Intext Educational Publishers.
2. Swan CC, Kosaka I (1997) Voigt-Reuss topology optimization for structures with linear elastic material behaviors. International Journal for Numerical Methods in Engineering 40: 3033- 3057.
3. Ashok D, Belegundu, Tirupathi R, Chandrupatla (1999) Optimization Concepts and Applications in Engineering. chapter 3. Prentice Hall.
4. Sigmund Ole, Torquato S (1999) Design of smart composite materials using topology optimization. Smart materials structures 8: 365-379.
5. Cox HL (1965) The Design of Structures of Least Weight. Pergamon Press.
6. Duhring, Maria B, Jensen, Jakob S, Sigmund, et al. (2008) Acoustic design by topology optimization. Journal of Sound and Vibration 317: 557-575.
7. Skidmore, Owings, Mirrell (2017) CITIC Financial Center.
8. Rosyid DM, Caldwell JB (1991) Design approach and dimensional similarity in lay-out optimization of steel structural systems. Computer and structures 40(5): 1125-1137.
9. Mijar, Anand R, Swan, Colby C, Arora, et al. (1998) Continuum Topology Optimization for Concept design of frame bracing systems. Journal of structural Engineering 124(5): 541-550.
10. Stromberg, Lauren L, Beghini, Alessandro Baker, William F, et al. (2013) Connecting architecture and Engineering through structural optimization. Engineering structures 59: 716-726.
11. Liang QQ, Xie YM, Steven GP (1999) Optimal Topology Selection of Continuum Structures with Displacement Contraints. Computers and structures 77(6): 635-644.
12. Liang, Quing Quan, Xie, Yi Min, Steve, et al. (2000) Optimal Topology design of bracing systems for multistory steel frame. Journal of Structural Engineering 126(7): 823-829.
13. Clausen, Anders, Aage, Neils, Sigmund, et al. (2016) Exploiting additive manufacturing infill in topology optimization for improved buckling load. Engineering (BeiJing) 2: 250-257.
14. Zegard, Tomas, Paulino, Glaucio H (2015) Bridging topology optimization and additive manufacturing. Structural Multidisciplinary optimization 53: 175-192.
15. Sousa, Luisa C Castro, Catarina F Antonio, Carlos C Sousa, Hipolito (2010) Topology optimization of masonry units from the thermal point of view of using a genetic algorithm. Construction and building materials 23: 2254-2262.
16. Stromberg, Lauren L, Beghini, Alessandro Baker, William F, et al. (2011) Topology Optimization for braced frames: Combining continuum and beam/column elements. Engineering structures 37: 106-124.
17. Stromberg, Lauren L, Beghini, Alessandro Baker, William F, et al. (2010) Application of layout and topology optimization using pattern gradation for the conceptual design of buildings. Structural and multidisciplinary optimization 43(2): 165-180.
18. Tingley DD, Davison B (2013) Minimizing the Environmental Impact of Steel Structures. Engineering Structures 97: PP. 651-656.
19. Goo, Zhen John, (2013) Topology Optimization of Building bracing schemes. A Masters of Engineering dissertation Massachusetts Institute of Technology Civil and Environmental Engineering.
20. Rietz A, Petersson J (2001) Simultaneous shape and thickness optimization. Structural and Multidisciplinary Optimization 23(1): 14-23.
21. Sigmund Ole, Andreassen Erik, Clausen Anders, Schevenels Mattias, et al. (2011) Efficient topology optimization MATLAB using 88 lines of code. Structural and Multidisciplinary optimization 43: 01-16.
22. Sigmund O (1994) Design of material structures using topology optimization. Report S69 Danish Center for Applied Mathematics and Mechanics.
23. Sigmund Ole (1999) A 99-line topology optimization code written in Matlab. Structural and Multidisciplinary optimization 21: 120-127.
24. Sigmund Ole, Ange Niels, Andreassen Erik (2015) On the (non-) optimality of Michell structures. Structural and Multidisciplinary optimization 54(2): 361-373.
25. Baldock, Robert (2007) Structural Optimisation in building design practice Case-study in topology optimisation of bracing systems. A PhD dissertation Cambridge University Engineering department.
26. Melanie (2014) History of the Sewickley Bridge – Sewickley PA.
27. Iyengar, Hal, Skidmore, Owings, Merrill, (2000) Reflections on the Hancock Concept. CTBUH review 1(1): 44-52.
28. Khan FR, Iyengar SH, Colaco JP (1966) Computer design of 100-story John Hancock Center. ASCE Journal of Structural Engineering 92 (ST6): 55–73.
29. Li, Gang, Ning, Hongchao, (2008) Seismic optimum design for the high-rise building with girder transfer floor. The 14th world conference on Earthquake Engineering 12-17.
30. Rietz A (2001) Sufficiency of a finite exponent in SIMP (power law) methods. Structural and Multidisciplinary Optimization 21: 159-163.
31. Sigmund Ole, Martin P Bendsøe (2004) Topology Optimization by Distribution of Isotropic Material. Topology Optimization: Theory Methods and Applications Springer pp. 1–68.
32. Zhou, Kemin, Chen, Chahua (2014) Topology optimization of frame bracing system for natural frequency. The Open Civil Engineering Journal 8: 250-256.