Extrapolation Techniques for Experimental Determination of Plates’ Buckling Loads

Extrapolation techniques are some plotting methods developed for experimental determination of buckling loads of structures, without the need for loading the structure in the vicinity of the critical. In addition to their simplicity, the extrapolation techniques have been considered useful in ‘smoothing’ the experimental data by removing most of the geometrical, material, and loading imperfection effects Singer [1], and hence are believed to provide an accurate measure of critical buckling load of real imperfect structures. Southwell [2], first, proposed a method for predicting the elastic buckling load of initially imperfect, concentrically loaded and pin-ended columns, which is known as the Southwell Plot. Then, Massey [3] developed the so-called Massey Plot method as a modified version of the Southwell’s method. Later on, another modified plotting technique, known as the Modified Plot method, was proposed by Trahair [4] as an alternative to the Massey Plot method. These methods are applied on load-displacement relationships obtained from the testing of the structures undergoing buckling. Southwell Plot graphs displacement/load against displacement and the slope of the obtained linear relationship between these equals the reciprocal of the critical load. Massey Plot, on the other hand, graphs displacement/load2 against displacement and the slope of the obtained straight line equals the square of the reciprocal of the critical load. Moreover, Modified Plot graphs displacement×load against displacement and the slope of the obtained straight line quals the critical load.

Extrapolation techniques have been used for predicting the buckling loads of a variety of thin-walled structures, e.g. beams, columns, frames, and conical shells. They have also been successfully applied on various deformation characteristics, e.g. displacements, rotations, and strains, for predicting the critical buckling loads of structural members. Attard [5], Attard and Bradford [6], Bradford and Wee [7], Mandal and Calladine [8], Zirakian [9,10], Zirakian and Nojoumi [11], Ghanbari Ghazijahani and Zirakian [12], dos Santos et al. [13], Slein et al. [14], Marcinowski et al. [15], and Virgin and Harvey Jr. [16,17] are among the numerous researchers who reported studies on the application of the extrapolation techniques.

This paper intends to demonstrate the applicability and investigate the performance of the Southwell, Massey, and Modified plotting methods in predicting the critical buckling loads of low yield point steel plates undergoing simultaneous geometrical buckling and material yielding with seismic applications such as in steel plate shear wall systems. To this end, a series of linear and nonlinear buckling analyses have been performed on plates with various aspect ratios as well as loading and support conditions, and the extrapolated and theoretical critical buckling loads have been compared and evaluated.

Design and Characteristics of Considered Plates

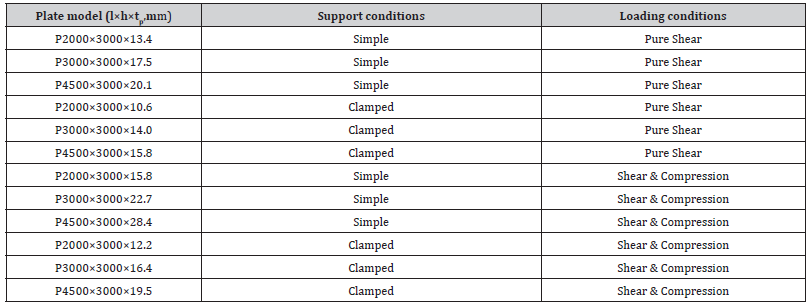
Twelve steel plates with different aspect ratios as well as simple and clamped support conditions subjected to pure shear and combined shear and (uniaxial) compressive loadings were considered in this study. The compressive load was considered to be proportional and literally 50% of the shear load. The plate thicknesses were determined by imposing concurrent geometricalmaterial bifurcation. Simultaneous geometrical buckling and material yielding occurs when the plate critical shear stress is equal to its shear yield stress. The plate shear yield stress was determined by considering the von Mises yield criterion. It is noted that the concurrent geometrical-material bifurcation may occur in thin-walled and plated structures/structural systems, e.g. steel plate shear walls as lateral force-resisting systems. In the theoretical calculations as well as finite element simulations, the elastic modulus Poisson’s ratio (𝝊), and yield stress of the low yield point steel material were taken as 200 GPa, 0.3, and 100 MPa, respectively. The characteristics of the considered plate models are summarized in (Table 1).

Table 1:Properties of the considered plate models.

Finite Element Modeling and Validation

ANSYS (2007) was used for the simulation of the plates. Linear eigen buckling analyses were performed for determining the elastic critical loads of the plates modeled using Shell63 elastic element. Also, nonlinear large deflection static analyses were performed for nonlinear buckling analysis of the plates simulated using Shell181 element. Uniformly distributed shear and compressive loads were applied along the middle plane of the edge nodes, and the corner nodes were given half the value of the middle ones. Proper boundary conditions were applied for developing simple and clamped supports. Low yield point (LYP100) steel material with a bilinear stress-strain relation was adopted for the nonlinear buckling analyses. Material properties were consistent with those applied in theoretical calculations. The tangent modulus was taken as 3333.3 MPa. Moreover, the von Mises yield criterion was used for material yielding, and the isotropic hardening rule was also incorporated in the nonlinear pushover analyses. In order to initiate buckling, a very small out-of-plane force of about 0.01% of plate elastic buckling capacity was applied at the center of the plate. Both geometrical and material nonlinearities were included in the analyses. The arc-length method was implemented to achieve a fast convergence and capture the unloading behavior of the plate. Convergence and mesh refinement studies were performed to ensure high accuracy in modeling as a result of which 100×100 mm elements were chosen through comparison of the numerical and theoretical predictions with discrepancies below 5%. The typical first buckling mode shapes of two typical plate models with simple and clamped support conditions subjected to pure shear are illustrated in Figures 1(a) & 1(b), respectively.

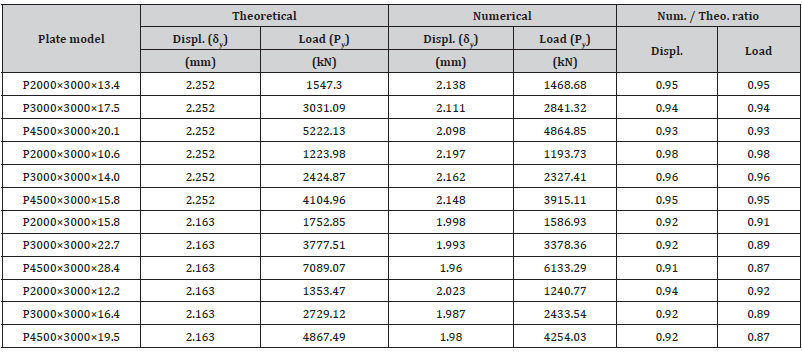
The theoretical and numerical predictions of the in-plane lateral displacement and shear load corresponding to the first yield point, i.e. and are compared in Table 2. Despite the nonlinearities in finite element modeling as well as the theoretical considerations, the agreement between the results is satisfactory. This is indicative of validity of the numerical simulation (Table 2).

Table 2:Comparison of the theoretical and numerical predictions of the first yield point.

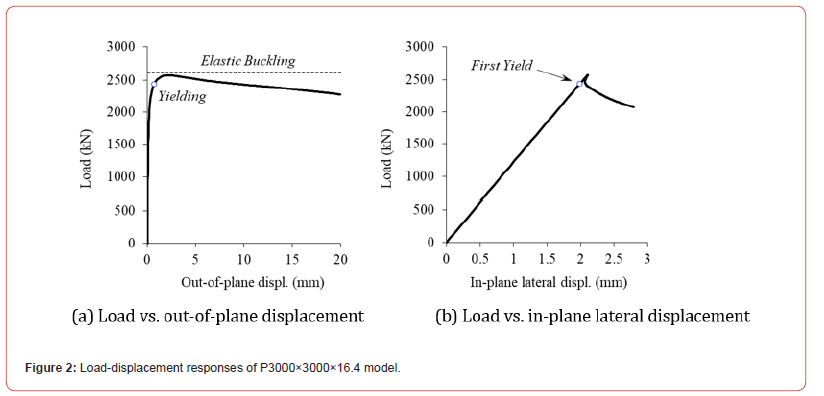
The typical load versus out-of-plane displacement as well as the load versus in-plane lateral displacement responses of the P3000×3000×16.4 model is shown in Figures 2(a) & 2(b), respectively. From the figures, it is evident that the plate undergoes simultaneous buckling and yielding. The plotted responses exhibit neither post-buckling nor post-yield reserves.

Application of Extrapolation Techniques and Discussion of Results

The Southwell, Massey, and Modified plotting methods were used to predict the critical loads of the plates. As illustrated in (Figure 3), the initial portions of the load-displacement responses with a parabolic shape up to the ultimate strength were used and the unloading portions were ignored.

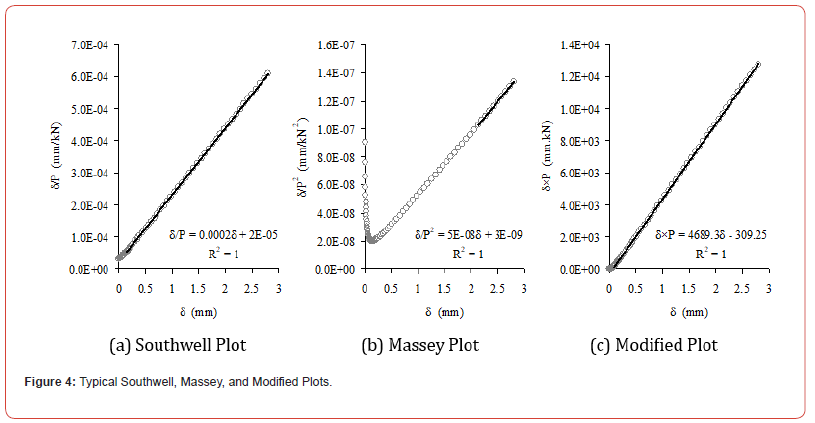
As seen in (Figures 2 & 3), due to concurrent geometricalmaterial bifurcation, the plate reaches its ultimate strength and unloading takes place. The ultimate strength of the plate is indeed an inaccurate measure of the critical load, and hence extrapolation techniques can be used to determine the buckling load corresponding to the theoretical critical load. (Figure 4) shows typical Southwell, Massey, and Modified plots for P4500×3000×19.5 plate model, where δ and P denote the out-of-plane displacement and shear load, respectively. From the figure it is evident that the Southwell and Modified Plots are superior to the Massey Plot because of their relatively extended range of linearity. Nevertheless, the Modified Plot exhibits the most extended range of linearity.

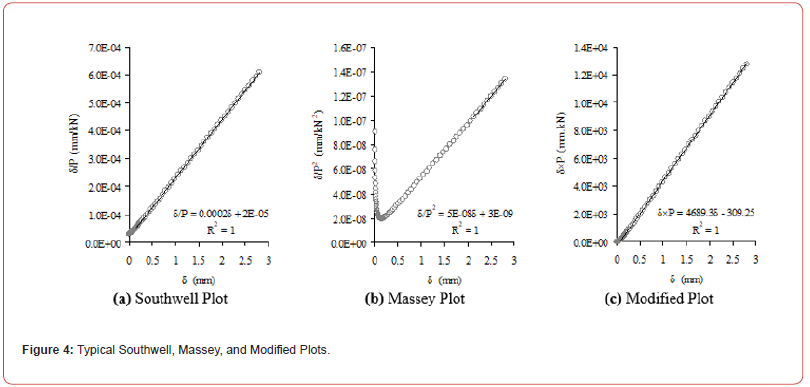
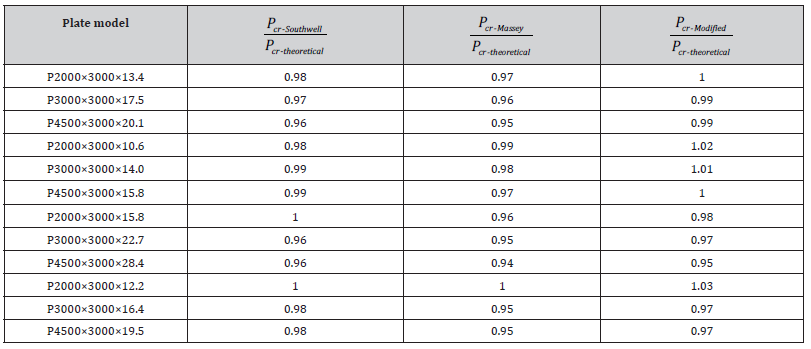
The extrapolated as well as theoretical critical load predictions of the plate models are presented in (Table 3). From the table, the high performance of the three plotting methods in successfully predicting the critical loads of the plates as compared to the theoretical predictions is quite evident. Quantitatively, the discrepancies between the extrapolated and theoretical predictions are found to be 2.0%, 3.5%, and 1.1%, on average, for the Southwell, Massey, and Modified methods, respectively. The higher performance of the Modified Plot in providing the most accurate predictions is evident. These findings are consistent with the results reported by Zirakian for the buckling of beams. Overall, the applicability and high performance of the three Southwell, Massey, and Modified extrapolation techniques in case of buckling of plates, especially with simultaneous geometrical-material bifurcation, are verified in this study. Experimental studies may further substantiate these findings.

Table 3:Comparison of the theoretical and extrapolated buckling loads.

Extrapolation or plotting techniques are experimental methods which have been developed for determining experimentally the critical buckling load of structures, without having to test them to failure. This paper reported a study on the application of the Southwell, Massey, and Modified Plots in case of plates undergoing simultaneous geometrical buckling and material yielding.

Concurrent geometrical-material bifurcation can be a significant parameter in the design and performance assessment of structural and seismic systems such as low yield point steel shear walls. The applicability and high performance of the Southwell, Massey, and Modified plotting methods in predicting the critical loads of such plates with respective 2.0%, 3.5%, and 1.1% discrepancies relative to the theoretical predictions were verified. Modified Plot was found to be the most efficient in predicting the buckling load. Experimental investigations are believed to further substantiate the findings of this research endeavor.

The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The author certifies that he has no affiliations with or involvement in any organization or entity with any financial interest, or non-financial interest in the subject matter or materials discussed in this manuscript.

1. Singer J (1989) On the applicability of the Southwell plot to plastic buckling. Experimental Mechanics 29(2): 205-208.
2. Southwell RV (1932) On the analysis of experimental observations in the problems of elastic stability. Proceedings of the Royal Society of London 135(88): 601-616.
3. Massey C (1963) Elastic and inelastic lateral instability of I-beams. The Engineer 216(5622): 672-674.
4. Trahair NS, AMASCE (1969) Deformations of geometrically imperfect beams. Journal of the Structural Division ASCE 95(7): 1475-1496.
5. Attard MM (1983) Extrapolation techniques for buckling loads. Journal of Structural Engineering ASCE 109(4): 926-935.
6. Attard MM, Bradford MA (1990) Bifurcation experiments on monosymmetric cantilevers. Proceedings of the twelfth australasian conference on the mechanics of structures and materials Brisbane pp. 207-213.
7. Bradford MA, Wee A (1994) Analysis of buckling tests on beams on seat supports. Journal of Constructional Steel Research 28(3): 227-242.
8. Mandal P, Calladine CR (2002) Lateral-torsional buckling of beams and the Southwell Plot. International Journal of Mechanical Sciences 44(12): 2557-2571.
9. Zirakian T (2008) Lateral-Distortional Buckling of I-Beams and the Extrapolation Techniques. Journal of Constructional Steel Research 64(1): 1-11.
10. Zirakian T (2010) On the Application of the Extrapolation Techniques in Elastic Buckling. Journal of Constructional Steel Research 66(3): 335-341.
11. Zirakian T, Nojoumi SA (2011) Elastic lateral–distortional buckling of I-beams and the Meck Plot. Structural Engineering and Mechanics 37(3): 297-307.
12. Ghanbari Ghazijahani T, Zirakian T (2014) Determination of Buckling Loads of Conical Shells Using Extrapolation Techniques. Thin-Walled Structures 74: 292-299.
13. dos Santos GB, Gardner L, Kucukler M (2018) A method for the numerical derivation of plastic collapse loads. Thin-Walled Structures 124: 258-277.
14. Slein R, Buth JS, Latif W, Kamath AM, Alshannaq AA, et al. (2021) Lateral-Torsional Buckling Research Needs and Validation of an Experimental Setup in the Elastic Range. Engineering Journal AISC 58(4): 279-291.
15. Marcinowski J, Sadowski M, Sakharov V (2022) On the applicability of Southwell’s method to the determination of the critical force of elastic columns of variable cross sections. Acta Mechanica 233: 4861-4875.
16. Virgin LN, Harvey JrPS (2023) A lateral–torsional buckling demonstration model using 3D printing. Engineering Structures 280: 115682.
17. ANSYS (2007) ANSYS 11.0 documentation, ANSYS Inc.