Basis of Probabilistic Semi-Explicit Cracking Model for Fiber Reinforced Concretes

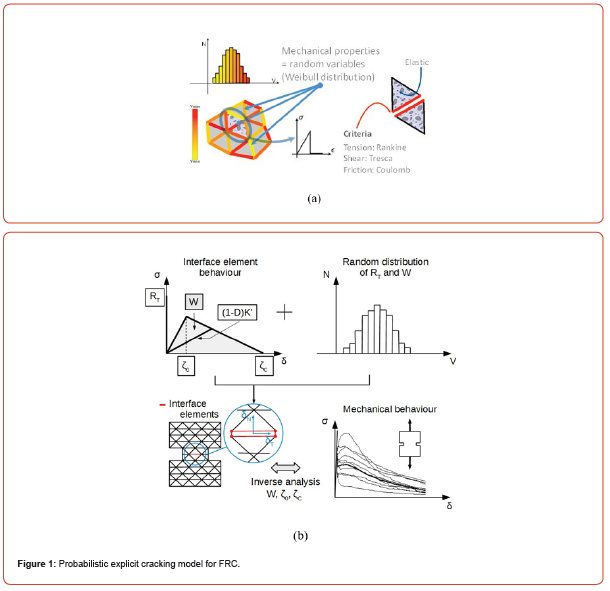
The probabilistic explicit cracking model for fiber reinforced concretes (FRC) was developed in 2015 [1, 2]. In this model, the creation of cracks in the concrete matrix is represented by an elastic perfectly brittle behavior. These cracks are modelled by using non-linear interface elements. These interface elements “open” when the tensile strength at their gravity center is reached (creation of a cinematic discontinuities representing explicitly cracks). The concrete tensile strength is considered as a random characteristic (following a Weibull law) that depends on the finite elements size. By this way the cracks creation in the matrix (the concrete) is independent of the finite element mesh. The bridging effect of the fibers is described as following: normal and tangential stresses in the interface element linearly increase with normal and tangential displacements when a “broken” interface element re-opens to consider the elastic bridging effect of the fibers inside the crack. When a threshold value, ζ₀, related to the normal displacement is reached, the normal stress is considered as linearly decreasing with the normal displacement in order to consider the damage of the bond between the concrete and the fiber, and fiber pullout. The decreasing evolution is obtained by using a damage model. Finally, the interface element is considered definitively broken when the normal displacement reaches a threshold value, ζ_c. This value corresponds to the state where the effect of fibers is considered negligible. At this point, its normal and tangential rigidities are set to zero. The post-cracking energy dissipated by the bridging effect of the fibers is considered randomly distributed over the mesh elements. The random distribution chosen is a log-normal distribution function with a mean value independent of the mesh elements size and a standard deviation, due to the heterogeneity of the material, increasing as the mesh elements size decreases [3].

Figure 1 presents the numerical mechanical behavior adopted to represent the experimental post-cracking behavior. Only the normal stress-normal displacement curve is considered in this figure. This model, that has been deeply validated [1, 2, 4-7], is very rele- vant to evaluate cracks opening for the service limit state situation of FRC structures (cracks opening ≤ 300 microns). The main limit of this modelling approach is related to the fact that cracks are modelled by interface elements that induces the use of high number of nodes (the non-linear interface elements interface all the volume elements of the finite element mesh) during numerical simulations. Then the computational cost becomes very important when the rupture of large structures analysis is concerned. Consequently, it is important to use more relevant approach for simulating the behavior of these large concrete structures. The development of a probabilistic semi-explicit cracking model for FRCs has for objective to solve this problem. The basis of this new model is to use linear volume elements to model macrocracks propagation. This choice is to reduce a lot of computational time. The mechanical behavior associated to these volume elements is based on the use of post-cracking dissipative energy for considering the bridging effect of fibers.

Existing diffused cracking models

These models do not consider cracks as real cinematic discontinuities but as microcracked zones in which the density of microcracks continuously increases until creating a kind of hole (no more stresses are transmitted). Numerically speaking, in the framework of finite elements theory, the microcracked zones are modeled by using volume elements. In these models, that are generally determined, the non-linear mechanical behavior (related to the microc racking process) of the volume elements is linked to the post-peak behavior in tension of the FRC. This post-peak behavior is generally characterized by two material parameters:
1. The shape of the post-peak (it means after the linear elastic part of the tensile behavior of the FRC) behavior of the tensile stress-strain curve.
2. The post-peak energy dissipation is related to the tensile stress-strain curve. This dissipation energy is very often called G_f.

To summarize, the diffuse cracking models, applied to FRC, are based on the use of non-linear finite elements method with volume elements. The non-linear behavior considered is that of the FRC in tension in the form of a relationship between the tensile stress and the tensile strain. It is important to note that, experimentally (and physically) speaking, the post-peak behavior of FRCs is related to the post-localization cracking, it means after the passage from diffused microcracking to localized macrocrack [8]. Then, it clearly appears that the diffuse cracking models are not physically based. From a practical point of view, the post-peak behavior in tension used as main mechanical characteristic in the diffused cracking models comes from the experimental tensile stress-crack opening curve. So, to pass from the experimental tensile stress-crack opening curve to the theoretical tensile stress-tensile strain used in the model, it is needed to introduce a length that permits to divide the crack opening value to get the “equivalent” tensile strain. In the majority of the diffused cracking models, this length is linked to the volume element size of the finite element mesh. This length chosen and used in the numerical simulation is very important because it permits, during the simulation, to transform the non-linear strains observed in crack openings.

These models that are, presently, the more described in literature and the more used in practice, have a great drawback. As was said before in the paper, the diffused cracking models are not physically based because they “transform” a localized crack in a diffused microcracking zone. This strong physical approximation leads to get a strong approximation of the cracking pattern of a given FRC structure. Numerically speaking, Gf values being a lot larger for FRCs than for normal concretes, the diffused cracking models lead to spread a lot the damaged (microcracked) zones and to underestimate the cracks opening. Therefore, these models don’t lead to a fairly reliable and secure response to the durability of FRC structures. The more well-known diffused cracking models for FRC are damaged models [9-11] and smeared crack models [12-15] that are mechanically equivalent. It can be noted that the smeared crack model developed at Ecole Polytechnique of Montréal (Canada) [14,15] gives better evaluation of the cracks opening of FRCs than the others diffused cracking models. That is due to the fact that it uses an explicit algorithm of resolution while the other models used an implicit algorithm of resolution. This choice leads to a better localization of the cracks. Despite this improvement, even the evaluation of the cracks opening.

The proposed cracking models

The semi-explicit cracking model has for first objective to avoid the mean default of the diffused cracking models. It means, it has to avoid too much diffusion of cracks leading to underestimate the opening of the larger cracks. To achieve this objective, two main assumptions are made:
The matrix (the concrete) has a brittle behavior before the bridging effect of fibers.
The tensile strength of the matrix is a random parameter.

So, these two assumptions are the same as that for the explicit cracking model evocated in the introduction. The main difference concerns the type of finite element used to model the crack creation and the crack propagation and also the scale of modelling. In the case of the explicit cracking model, cracks are modelled by using non-linear interface elements and in the proposed semi-explicit cracking model, cracks are modelled by using linear volume elements. This difference has a strong consequence on the modelling of cracks initiation and propagation, especially when a perfect brittle behavior of the material is considered. Indeed, it has been clearly shown [16] that, in this case, the cracks initiation and propagation are not correctly modelled. In the case of FRC modelling, this strong approximation made on the matrix cracking can be considered as acceptable if the bridging effect of fibers is correctly considered in the model. This affirmation is supported by the fact that, physically speaking, the energy dissipation related to the matrix cracking is very small compared to the energy dissipation due to the bridging effect of fibers. It is also important to specify that the semi-explicit model for FRCs is devoted to macrocracks propagation in large structures. So, the size of the volume elements used in the numerical simulations should be also larger than those used for the explicit cracking model. To summarize the above and to give details, the probabilistic semi-explicit cracking model will have the following characteristics:
1. It will use linear volume elements (for reduction of simulation time).
2. The cracking creation will occur when the tensile strength at the gravity point of the volume element will reach the strength of the matrix (concrete without fibers). A perfect brittle of the matrix is considered.
3. The concrete strength is a random parameter (Weibull distribution) will depend on the volume of the finite elements. The mean value and the standard deviation of the matrix tensile strength will decrease with the volume of the finite elements [1-7, 17].

To complete the mechanical model proposed for FRCs, it needs to specify how the bridging effect of fibers will be considered. For that, it is proposed to choose similar approach than for the explicit cracking model (Figure 1).

Similar but not identical. In the explicit cracking model, the bridging effect is considered through a very simple model (see introduction) characterized by a random post-cracking energy. In the semi-explicit cracking model, that concerns macrocracks propagation with openings superior to or equal to 300 microns, the volume elements are much larger than those used in the case of the explicit cracking model. Previous experimental research [3] demonstrated that the mean value of the post-cracking energy due to bridging effect is independent of the volume of material tested and that the standard deviation related to this energy decreases with this volume. So, it is decided, in relation with the objective of the present model (it means to model macrocracks propagation in large FRC structures) to simplify the modelling approach by considering a bridging effect dissipation energy (G_f) will be a deterministic parameter independent of the volume of the finite elements.

Mechanical aspects

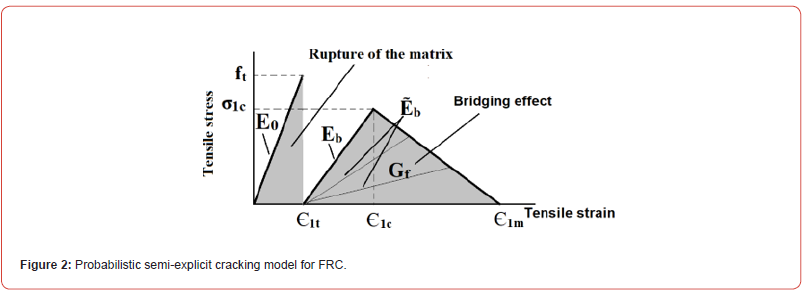
The probabilistic semi-explicit cracking model works as following:
1. First step: a crack (in fact, a hole) in the finite element occurs when the maximum principal stress (σ1) reaches the random material tensile strength (ft) at a given Gauss point. Then elementary stiffness matrix of the element is set to a very low value (~10-10).
2. Second step: Two situations can exist:
 The maximum principal strain (є1) decreases. In this case, the elementary stiffness matrix of the element keeps its very low value.
 The maximum principal strain increases. In this case, the bridging effect is active.
 The elementary stiffness matrix of the element increases a lot of to consider the elastic bridging effect of fibers. This new elementary stiffness matrix (Eb) has to be, of course, inferior to that of the material before cracking (E0).
3. Third step: є1 reaches a critical value (є1c). σ1 decreases linearly with є1 (descending branch). This decrease represents the progressive pull-out of the fibers. When є1 reaches a maximum value (є1m), fibers action is considered finished, and the elementary stiffness matrix of the element is set to zero. This softening behavior is modelled through the use of simple damage parameter (damage model). Only the values of the elementary matrix related the relation between the maximum principal stress and the maximum principal strain. The rest of the values of the elementary matrix remain equal to zero. By this way, the bridging action of fibers is considered as anisotropic.

The complete mechanical behavior of a volume element is schematized in Figure 2.

Numerical aspects

Numerically speaking, it will be used as a classical implicit resolution scheme. The fact that the proposed model is partly probabilistic (the tensile strength is a random parameter) imposes to use the concept of the more dangerous element to get numerical simulations independent of the loading increments. This concept was developed and used with success in the frame of the probabilistic explicit cracking model [1-7, 18-22]. Its use, in the frame of the implicit numerical scheme proposed, is very simple. It can be presented as following:
1. A total increment of loading is chosen. From there, a first sub-increment is calculated to permit to “crack” only one volume element (its elementary matrix is set to a very low value), the more dangerous one. This more dangerous volume element is volume element for which the difference between its maximum principal stress and its tensile strength is larger. This element “cracked”, the stresses and strains fields are calculated to get the equilibrium.
2. The second sub-increment is calculated to crack the second more dangerous element (its elementary matrix is also set to a very low value). After this second more dangerous element cracked, the equilibrium is calculated by considering new values of the elementary matrix of the first more dangerous element (Eb in figure 2). All the sub- increments are determined in this way until the target total loading increment is reached.
3. During each sub-increment, when the maximum principal strain related to a volume element reaches the critical value, Є_1c, the elementary matrix of this volume element is modified as presented in Figure 2 (Figure 2).

4. Determination of the model parameters

In the proposed model, its parameters are determined as following:
1. The mean tensile strength of the matrix, f_t, and the standard deviation related to this strength (function of the volume of the finite element) are calculated using the formulas of Rossi et al. [17] deeply validated in the past [1-7,18-24].
2. The fibers bridging energy, G_f, is obtained by performing uniaxial tensile tests on notched specimens [23, 24]. As previously said in the paper, the mean value of this energy is independent of the specimen size, but its standard deviation increases when the specimen size decreases [3]. So, to get a correct value of Gf, it is important to adapt the number of specimens tested to its size.
3. є_1m is obtained from the tensile test on the notched specimen. It is the strain that corresponds to the lowest value of the tensile stress related to the bridging effect of fibers.

In the tensile tests, only cracks opening is got. So, for the model (and the numerical simulations), it is necessary to transform the opening in strain. To achieve this transformation, it is chosen to use a classical method that consists to divide the crack opening by a characteristic length of the volume elements. The characteristic length proposed is 1e=V_e^1/3(V_e is the volume of the finite element). 4. σ1c is the larger value of the tensile stress related to the bridging effect of fibers. 5. Eb is easily calculated knowing the others values of the model parameters.

Since the numerical model is probabilistic (though the use of ft as random parameter), a Monte Carlo procedure must be used to provide statistically consistent results.

This paper presents the basis of a new model for FRC cracking. It is a probabilistic semi-explicit cracking model. Its objective is to model macrocracks propagation in large FRC structures. In this model, it is proposed to simulate cracks propagation by using linear volume elements. The mean assumptions of this model are the consequence of a critical analysis of existing models of literature (treating the same problem). These mean assumptions are the following:
 The matrix (the concrete) has a brittle behavior before the bridging effect of fibers.
 The tensile strength of the matrix that governs the cracks creation is a random parameter.

The bridging effect of fibers is modelled through a very simple deterministic damage model. The principles of the numerical algorithm scheme of the proposed model is presented in detail. The way to determine the values of the model parameter is also presented in detail. This determination involves the use of a uniaxial tensile test on notched specimens. For the future, the numerical development of this new model has to be achieved and its validation has to be made by using results from literature.

None.

No conflict of interest.

1. Rossi P, Daviau-Desnoyers D, Tailhan JL (2015) Analysis of cracking in steel fiber reinforced concrete (SFRC) structures in bending using probabilistic modelling. Structural Concrete 16(3): 381-388.
2. Tailhan JL, Rossi P, Daviau-Desnoyers D (2015) Numerical modelling of cracking in steel fiber reinforced concrete (SFRC) structures. Cement and Concrete Composites 55: 315-321.
3. Rossi P (2012) Experimental Study of Scaling Effect Related to Post-Cracking Behaviors of Metal Fibers Reinforced (MFRC). European Journal of Environmental and Civil Engineering 16(10): 1261-1268.
4. Rossi P (2016) Numerical models for designing steel fiber reinforced concrete structures: why and which ones? In: B Massicotte, JP Charron, G Plizzari, B Mobasher (Eds.) FRC 2014: ACI-fib International Workshop, FIB Bulletin 79-ACI SP-310, 289-300, 2016.
5. Rossi P, Tailhan JL (2017) Numerical modelling of the cracking behavior of steel fiber reinforced concrete (SFRC) beam on grade, Structural Concrete, 18 (4): 571-576.
6. Rossi P, Daviau-Desnoyers D, Tailhan JL (2018) Probabilistic Numerical Model of Ultra- High-Performance Fiber Reinforced Concrete (UHPRFC) Cracking Process. Cement and Concrete Composites 90: 119-125.
7. Tailhan JL, Rossi P, Salin D (2022) Design Optimization of Concrete Railway Tracks by Using Non-linear Finite Element Analysis. In: P Rossi, JL Tailhan (Eds.) RILEM International Conference on Numerical Modeling Strategies for Sustainable Concrete Structures (SSCS’2022), pp.345-354.
8. Rossi P, Acker P, Malier Y (1987) Effect of steel fibers at two different stages: the material and the structures. Materials and Structures 20: 436-439.
9. Fanella D, Krajcinovic D (1985) Continuum damage mechanics of fiber reinforced concrete. J Eng Mech 111(8): 995-1009.
10. Li F, Li Z (2000) Continuum damage mechanics-based modeling of fiber reinforced concrete in tension. Int J Solids Struct 38: 777-793.
11. Peng X, Meyer C (200) A continuum damage mechanics model for concrete reinforced with randomly distributed short fibers. Comput Struct 78: 505e515.
12. Barros JAO, Figueiras JA (2001) Model for the analysis of steel fiber reinforced concrete slabs on grade. Computers & Structures 79(1): 97-106.
13. Cunha V, Barros J, Sena-Cruz J (2012) A finite element model with discrete embedded elements for fiber reinforced composites. Computers & Structures 94-95: 22-33.
14. De Montaignac, R Massicotte, B Charron JP (2013) Finite-element modelling of SFRC members in bending. Magazine of Concrete Research 65(19): 1133-1146.
15. Lagier F, Massicotte B, Charron JP (2016) 3D Nonlinear Finite-Element Modeling of Lap Splices in UHPFRC. Journal of Structural Engineering 142(11).
16. Rodrigues Rita M (2022) Implementation of a macroscopic probabilistic model of cracking concrete using parallelization strategies. PhD Thesis of Federal University of Rio de Janeiro.
17. Rossi P, Wu X, Le Maou F, Belloc A (1994) Scale effect of concrete in tension. Materials and Structures 27: 437-444.
18. Rossi P, Wu X (1992) Probabilistic model for material behavior analysis and appraisement of concrete structures. Magazine of concrete research 44(161): 271-280.
19. Rossi P, Ulm FJ, Hachi F (1996) Compressive behavior of concrete: physical mechanisms and modeling. Journal of Engineering Mechanics 122(11): 1038-1043.
20. Phan TS, Tailhan JL, Rossi P (2013) 3D numerical modelling of concrete structural element reinforced with ribbed flat steel rebars. Structural Concrete 14(4): 378-388.
21. Phan TS, Rossi P, Tailhan JL (2015) Numerical modelling of the concrete/rebar bond in a reinforced concrete structural element: a multi-scale approach. Cement and Concrete Composites, pp.1-9.
22. Rodrigues Rita M (2022) Implementation of a macroscopic probabilistic model of cracking concrete using parallelization strategies. PhD Thesis of Federal University of Rio de Janeiro.
23. Rossi P, Harrouche N (1990) Mix design and mechanical behavior of some steel-fiber- reinforced concretes used in reinforced concrete structures. Materials and Structures 23: 256-266.
24. Rossi P (1992) Mechanical behavior of metal-fiber reinforced concretes. Cement and Concrete Composites 14: 3-16.