Analysis and Prevention of Forced Vibration and Resonance Mechanism of Machine Foundation in A Petrochemical Plant

Resonance occurs when the frequency of an external force is close to the natural frequency of an object, resulting in a strong vibration phenomenon. Resonance phenomenon are inseparable form people’s lives. For example, microwave ovens use electromagnetic waves to resonate with water molecules, heating food; the medical field utilizes magnetic resonance imaging to detect early lesions in patients; seismographs are designed based on the principle of mechanical resonance to detect earthquakes. However, everything has two sides, and the disasters caused by the forced resonance of structures are not uncommon. For example, the frequency of the march of German soldiers resonated with the bridge, causing the bridge to collapse. The Tacoma Narrows Bridge shook and col lapsed in high winds. The resonance between the Humen Bridge and wind load causes the bridge panels to vibrate greatly.

Resonance phenomenon is closely related to people’s lives, which has attracted the attention of scholars at home and abroad. The rapid development of vibration theory was accelerated only after the proposal of the thin plate vibration equation [1,2]. The research achievements of domestic scholars are mainly as follows. For the vibration analysis of a rectangular thin plate, the function expression and vibration frequency equation are provided, and the corresponding forced vibration of a rectangular thin plate is analyzed [3]. The expression and frequency equation of the correct mode function of the first-order natural frequency for rectangular thin plates with one pair of simply supported edges and another pair of free edges are provided [4]. The principle of virtual work is used to verify the correctness of the theorem of mutual equivalence of work in the small deflection bending problem of thin plates, and a formula for determining the natural frequency of thin plates is proposed [5]. The uncertainty in identifying structural vibration modal parameters of bridge structures under environmental excitation is quantified using Bayesian theory [6,7]. Considering the damping effect, the analytical solution and green function solution of the multi-crack curved beam under forced vibration were solved, and the influence of geometric and physical parameters on vibration response and the interaction between cracks were analyzed [8]. Based on the Laplace transform, explicit analytic expressions of axial free vibration and forced vibration displacement response, and their periodic peaks under different numerical conditions of damping, stiffness and mass were obtained [9]. The modal identification of pump stations under various vibration test conditions reveals that the domestic units are aging significantly, leading to local resonance hazards that affect structural safety during operation [10]. By addressing the challendes of vibration testing blindness and mode identification passivity, analytical expressions for the structure’s frequency, damping ratio, and mode variation coefficient are derived [11].

Foreign scholars assumed that the displacement function of a plate is composed of a double Fourier series, adopted the Hamiltonian principle, and discussed the free vibration problem of a four-sided simply supported laminated composite plate with additional distributed mass [12]. The high-order plate-shell theory is used to solve the free vibration problem of bidirectional orthogonal composite plates [13]. The free vibration characteristics of rectangular thin composite plates are analyzed using the Galerkin method, taking into account the stiffness of additional mass [14]. The actual vibration signal is obtained through field dynamic testing, which has been widely utilized in practical engineering [15]. The concept of the “law of uncertainty” was proposed to understand the mechanism and influencing factors of uncertainty in structural dynamic testing [16]. For environmental excitation testing, the uncertainty law has been successively developed under spares mode [17] and dense mode [18], revealing the internal mechanism of identification uncertainty formation. The forced vibration of rectangular thick plates under different boundary conditions is studied using the boundary integral method. The governing equations and bending surface equations applicable in engineering practice are obtained [19].

This paper presents the basic theory of forced vibration and resonance, as well as the principles of Fourier transform. Based on a case study of mechanical foundation resonance in a petrochemical plant in Zhejiang Province, the natural vibration signal of the foundation was collected using a vibration pickup instrument and analyzed by Fourier transform to determine the natural vibration frequency of the foundation. The natural vibration frequency of the foundation is adjusted by changing the mass and stiffness of the foundation to avoid forced resonance between the foundation and the machine.

Forced vibration and resonance

According to the Bohr vibration test, the forced vibration of the structure under external periodic load is obtained:

Where J is the moment of inertia of the balance wheel,M₀ is the amplitude of the driving torque, and ω is the angular frequency of the driving torque.

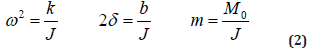
From the above definition, formula (1) can be rewritten as follows：

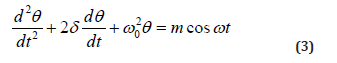
Where δ is the damping coefficient and ω₀ is the natural frequency of the balance wheel system. Under the condition of small damping (δ²−ω²) , the general solution of equation (3) is:

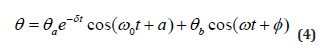
It is shown that the forced vibration of the balance wheel includes damping vibration and periodic vibration with the same frequency as the driving force and the amplitude of θ_b. When the damping vibration attenuates continuously to the point where it can be ignored, the forced vibration reaches a stable state. At this time, the forced vibration becomes simple harmonic vibration.

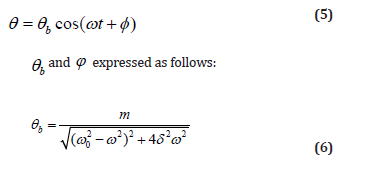
It can be concluded from the extreme value condition ∂θ_b/∂ω =0 that when the angular frequency of the driving torque 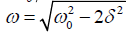, the amplitude of the forced vibration reaches the maximum and resonance is generated. The angular frequency ω_r, amplitude θ_r and phase difference ϕ_r during resonance are expressed as:

Equation of motion of forced vibration

The forced vibration of the foundation is simplified as the forced vibration of the system of single degrees of freedom, and the vibration of the foundation is driven by the rotation of the power machine. Based on the basic mass-spring-damping theory, the vibration of the foundation driven by the power machine in the vertical direction is assumed to be the inelastic external load of the dynamic foundation and the foundation is assumed to be massless elastomer. When the foundation is subjected to the cyclic load sin P_Z=P_Z sin ωt of the power machine in the vertical direction, the mechanical model can be simplified as shown in Figure 1.

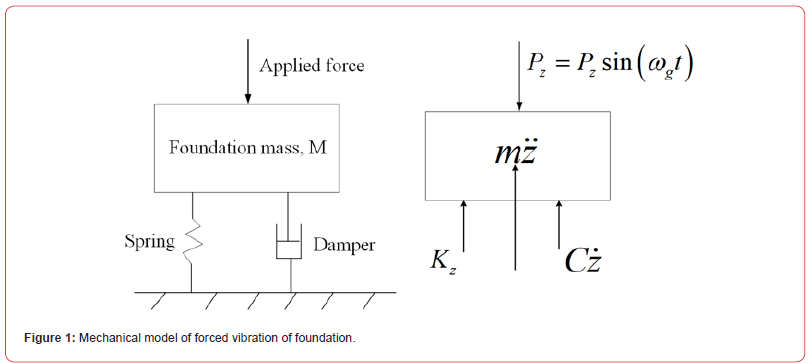
The motion equation of the foundation under vertical periodic load is expressed as follows:

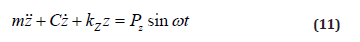
− Vertical vibration displacement of foundation (m), z − Vibration velocity (m / s) , z− Vibration acceleration (m/s²), m− The total mass of the power machine and the foundation (t) , C−Damping coefficient,K_Z − Foundation compressive stiffness (kN/m) ,P_z− Vertical disturbance amplitude of machine (kN) , ω − Machine circular frequency, ω = 2π f means the vibration frequency(H_z),t − Time (s) .

The vertical vibration amplitude A_Z of the foundation can be obtained by equation (8)

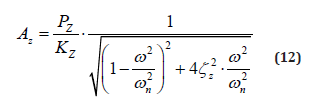
Where ω_n = 2πf_n,f_n is the undamped natural frequency of the power machine foundation (H_Z), ζ_z is the vertical vibration damping ratio of foundation.

Fast Fourier Transform (FFT) FFT algorithm derivation:

A. The formula for calculating the dual node value for the L iteration:

Where K_L is the loop control variable.
B. The relationship between dual nodes is shown in Figure 2.
i. Rotation factor:W_N^k N W is called rotation factor and it can be calculated and saved in advance.
ii. Round order: After r iterations, the result x_r((k₀k₁...k_r-1)_b)is obtained. While the actual result should be X((k_r-1....k₁k₀)_b), so the last step in the process is to round the result in the normal binary order of the subscript.

FFT algorithm flow:( N = 2r )

Initialization: x₀(n)←x(n),0≤n≤N−1

The L(1≤L≤r) iteration:
i. Subscript control variable initialization K_L=0
ii. Initialization of the number of “node pairs” num = 0
iii.While (num< N/2^L)DO

 The values of x_L(K_L) and x_L(K_L) are obtained by the set operation according to the calculation formula of dual node pairs.  K_L ← K_L +1 , num←num+1;  Skip the nodes that have already been calculated (These are the nodes that L K corresponds to above): K_L+= N/2^L  If K_L < N , go to (b) and continue to compute the next set of nodes, otherwise end this iteration. (iii) After r iterations are completed, the results are sorted by subscript binary bits to obtain the final results X (k)(0 ≤ k ≤ N −1) (Figure 2).

Case Analysis

Power machine rated power is 700KW, operating at 3000r per minute, with a weight of 5500kg, and a frequency of 50 Hz. The base is a steel-concrete composite structure, as shown in Figure 3. The base concrete type is C35, and the steel type is Q234B. The base is 3.65 meters long, 1.2 meters wide, and 1.35 meters high. Figure 4(a) illustrates the dimensions of the front facade of the base, while Figure 4(b) displays the dimensions of the base plane. The base experiences forced vibration and resonance during the operation of the power machine, which significantly impacts the machine`s normal operation. Additionally, the foundation shows signs of potential destruction. Therefore, the fundamental frequency of the base is measured using dynamic signal testing and analysis software and the D1000 general data acquisition instrument, and precautions are taken to prevent resonance.

Strength and flatness measurement

The levelness in the X and Y directions of the four bolts connecting the foundation to the machine was measured using a level. The results show that the reference bubbles of the level are in the middle of the scale, proving the levelness meets the requirements, as shown in Figure 5. As shown in Table 1, the strength of the concrete of the foundation structure is tested by the resilient meter. The strength of the upper concrete is presumed to be 28.3MPa and the strength of the lower concrete is presumed to be 39.5MPa, which meets the requirement of greater than C20. The Leeb hardness testing instrument was used to test the steel of foundation. The inferred tensile strength of the steel member was between 386MPa and 469MPa, and the conversion results meet the requirements of Q235 strength grade, which is shown in Table 2. The detection location of concrete and steel strength are shown in Figure 6.

Table 1:Strength measurement of concrete for the foundation.

Table 2:Leeb hardness of steel members and conversion values of tensile strength.

Vibration frequency detection

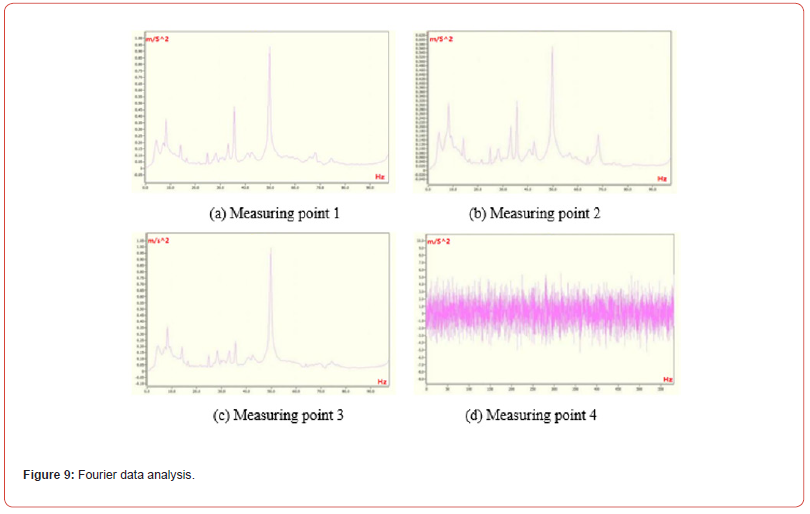
The acceleration vibration pickup instrument was used to detect the natural vibration frequency of the machine foundation. And the measurement points were located in the upper and lower part of the foundation, with a total of 4 measurement points. The actual field signal collection is shown in Figure 7. The actual data collection is shown in Figure 8, and the Fourier analysis of the vibration signal is shown in Figure 9.

Through the analysis of the measured data of the upper two points and the lower two points of the foundation, it can be seen that the natural vibration frequency of the foundation is about 50Hz, which is very close to the machine’s famous natural vibration frequency of 50Hz. Therefore, it is easy to resonate with the foundation during the work of the machine.

Conclusion

Under the condition that the flatness, concrete strength, and steel structure strength meet the requirements, the vibration frequency of the foundation is close to the operating frequency of the machine, making it prone to resonance. To prevent potential harm from resonance, adjusting the structural stiffness and mass to alter the natural vibration frequency of the structure and increasing the disparity between the vibration frequency of the structure and the machine can effectively prevent resonance and ensure the safe operation of the equipment.

Foundation

This article was supported by two foundations: 1. The Graduate First-class Curriculum Cultivation Project of Nanjing Forestry University. Project number: 163330008. 2. The research on crack propagation of bolt joints in steel structures based on Peridynamics of China Construction Seventh Division (Shanghai) Co., LTD. Project number: CSCEC-2022- Z-10.