A Field-View on the Generation of a Single Neural Pulse and Delay in Neighboring Pulses

To fully reveal the physical nature of a neural signal is important for understanding the ways how neural signals are generated and transmitted. Compared with the cable model and electromechanical model, the emerging electromagnetic model attracted much attention in recent years [1-5], as it states that neural signals travel in axons are more like pulses of electromagnetic (EM) waves travelling in EM waveguides, rather than ionic currents transporting in cables. Here we reanalyzed experimental data in published in previous literatures, and calculated the average delay time at each Ranvier node in myelinated axons with electromagnetic model, and figured out a picture on the underlying relationship between the generation process and the measured propagation speed for neural signals along axons. The propagation of neural signals in myelinated axons is measured with an average speed of 10-150 m/s [6]. Note that there are no reasonable physical processes with this similar velocity. For example, electromagnetic signals transmit at the light or near-light speed, 3×10⁸m/s, the migration of molecules in solution usually has a rate of 1nm/s driven by the electric field of 1V/m. Although the transmission of mechanical waves has similar velocity, it is obviously not the nature of neural signals. As a result, the measured propagation speed is the superficial speed, rather than the conduction speed of real neural signals.

Usually, the total delay of neural signals, behaving as action potentials, can be divided into two parts: delay on internodal segments, and delay at Ranvier nodes, i.e., ion channel group. Obviously, the delay on internodal segments could be overlooked in electromagnetic model. Because the velocity of the neural electromagnetic pulses is nearly the light speed, it needs only about 10-11 s for a neural signal to pass a single internodal segment of 1-2mm. As a result, the delay consumes mainly at Ranvier nodes, where the neural electromagnetic pulses relay (generated and amplified). According to the average internode length and measured propagation speed of neural signals at the same myelinated axons, average delay, τ, at Ranvier nodes could be calculated as

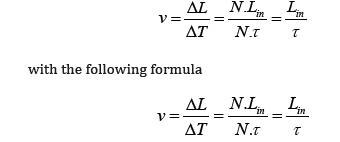
where ΔL is the distance between two points under test, ΔT the total delay time between these two testing points, N the number of Ranvier nodes between two testing points, and Lin the average internode length at the myelinated axon. Calculated with experimental data, the average delay τ was found ranging from 16.3 to 87.0 μs. These values are consistent with the value of 10-50 μs obtained in direct measurement [7], and also consistent with the value of 74 μs (named internodal conduction time) reported by Koles et al. [8]. Surprisingly, this DELAY occupies only 0.5-5% of the duration of a single action potential, which is usually measured to be 1-2 ms in numerous experiments.

Thus the reality in propagation of action potentials is not as described in textbook: an action potential is generated by ion channel cluster at one local spot, then transmits along an axon, and triggers excitation of next ion channel cluster. Indeed, within 100 μs after the first action potential is generated, the next action potential is triggered; and, the first one continuously develops into a full signal peak as measured, together with the second. Due to these two experimental facts: the similarity of action potentials and shorter delay (<100μs) in signal relay process, we schematically illustrate that two action potentials measured at two neighboring different nodes are overlapped highly in the same time scale, as shown in Figure 1.

It is reasonable to attribute the delay to the relay time of neural signals, including two processes: waiting/sensing time in which the neural electromagnetic signals increase from zero up to the threshold value capable of activating the open the next channels, and open process of ion channels. In electromagnetic model, the electric field impulse, i.e., the change rate of electric intensity, is the activating factor for open of voltage-gated ion channels. The 3D structure of this kind of channels has been rebuilt to has several functional groups, in which the polypeptide chains with dipole moment (if so) floating in solution are believed to behave as receiving antenna. As a result, it takes time for ion channels to open until the electric field change rate reaches up to a specific threshold. Our recent simulation on transmembrane ionic transport through a single nano-scale channel shows that, once the nano-channel opens, a transmembrane ion current could saturate at a few pA within 100 ns. This time is much less than the signal delay time at each Ranvier node (10~80 μs). The difference might come from the fact that, the open process of a single ion channel needs a long time, and the collective effect for opening a group of ion channels at one node further expends the total time slot. The open process of protein channel might need 10 μs or longer, while the distribution density of ion channels at Ranvier nodes of myelinated axons was measured to be around 1000/μm2 [9], and the density was around 5-50/μm² for unmyelinated axons [10]. This viewpoint is supported by some experimental evidence. For example, one work showed that the larger the stimulation intensity (E), the shorter the delay; and the relay time was stable when the stimulation intensity was near the threshold for triggering ion channels open [11]. In short, we have demonstrated that neighboring action potential peaks along a myelinated axon are highly overlapped in time zone. The shift in time of any two successive signals is less than 100 μs, thus is less than 10% of the average period of an action potential (1~2 ms). This shift in time, defined as delay time τ in this work, is attributed to the waiting time for the signal source at one node (i.e., ion channel clusters) to sense the signal sent from previous node, which appeared as attenuated electromagnetic field, to reach a threshold level for triggering ion channels. This mechanism may also be applied to unmyelinated axons.

This seems an overlooked scenario. It may help to understand the mechanism for electrical communication in neural systems, e.g., the brain.

This work was financially supported by the National Key R&D Program of China (No. 2017YFA0701302).

No conflict of interest.

1. J Xue, S Xu (2012) Natural electromagnetic waveguide structures based on myelin sheath in the neural system. Quantitative Biology.
2. S Xu, J Xu, F Yang (2016) The Roles of Membrane for Electrical Communication in a Biosystem. Neuroscience & Biomedical Engineering 4: 230-236.
3. J Xu, Y Xu, W Sun, M Li, S Xu (2018) Experimental and Computational Studies on the Basic Transmission Properties of Electromagnetic Waves in Softmaterial Waveguides. Scientific Reports 8: 13824.
4. J Xu, F Yang, D Han, S Xu (2018) Phenomena of simultaneous reaction in biosystems and the possible mechanism, Biomedical and Biophysical Research Communications 496: 661-666.
5. A Zangari, D Micheli, R Galeazzi, A Tozzi (2018) Node of Ranvier as an Array of Bio-Nanoantennas for Infrared Communication in Nerve Tissue, Scientific Reports 8: 539.
6. MF Bear, BW Connors, MA Paradiso (2007) Neuroscience: Exploring the brain (3rd ed.), Lippincott Williams & Wilkins.
7. M Rasminsky, TA Sears (1972) Internodal Conduction in Undissected Demyelinated Nerve Fibers. Journal of Physiology London 227: 323-350.
8. ZJ Koles, M Rasminsky (1972) A computer simulation of conduction in demyelinated nerve fibres. J Physiol 227: 351-364.
9. SG Waxman, JM Ritchie ((2010)) Molecular dissection of the myelinated axon, Annals of Neurology 33: 121-136.
10. H Hua, J Peter (2014) A supercritical density of Na (+) channels ensures fast signaling in GABAergic interneuron axons, Nature Neuroscience 17: 686-693.
11. I Hodler, R Stampfli, I Tasaki (1952) Role of potential wave spreading along myelinated nerve fiber in excitation and conduction. Am J Phys 170: 375-389.