 Opinion
Opinion
The Cot-X Family of Distributions with Application
Clement Boateng Ampadu, Department of Biostatistics, USA.
Received Date: August 18, 2019 Published Date: August 20, 2019
Abstract
We modify the cotangent function into a new statistical distribution and show its applicability.
Keywords: Trigonometric functions; Statistical distributions; Breast cancer; Odds T-X Contents
Introduction
Statistical distributions arising from trigonometric functions
have populated the literature, and for example, see [1-4]. On the
other hand, the T-X(W) family of distributions appeared in [5], and
in the special case the random variable T has support [0, ∞), and
the weight function is given by 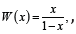 we get the so-called Odds
T-X family of distributions with the following integral representation
for its CDF
we get the so-called Odds
T-X family of distributions with the following integral representation
for its CDF
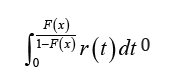
where the random variable X has CDF F (x) and the random variable T has PDF
By these observations, this paper unfolds as follows. We introduce a so-called Cot-X family of distributions in Section 2, and in Section 3 we introduce a so called Cot Odds T-X family of distributions. Section 4 and Section 5, show applicability of the new families, and the last section is devoted to the conclusions.
The New Family
The CDF of Cot-X is defined as
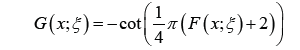
where x ∈ R, the baseline distribution has CDF F (x; ξ) and PDF f(x; ξ). By differentiat-ing the CDF, the PDF of Cot-X is given as
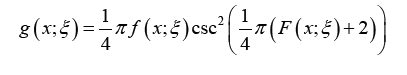
A New Variant of the Odds T-X Family of Distributions
Let T be a random variable with support [0, ∞), whose PDF and CDF are given by r(t; ξ) and R(t; ξ), respectively, with ξ being a vector of parameters in the distribution of T , and let X be a random variable with PDF f(x; β) and CDF F (x; β), where β is a vector of parameters in the distribution of X. We define the Cot Odds T-X family of distributions with the following integral for its CDF
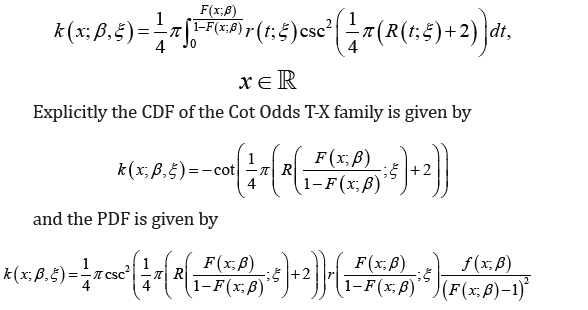
Practical Illustration of Cot-X
We assume X is a Dagum random variable with CDF
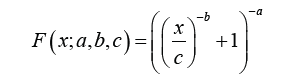
for x, a, b, c > 0. Now from Section 2 we have the following Proposition 6.1. The CDF of Cot-Dagum is given by
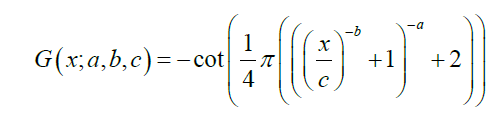
where x, a, b, c > 0
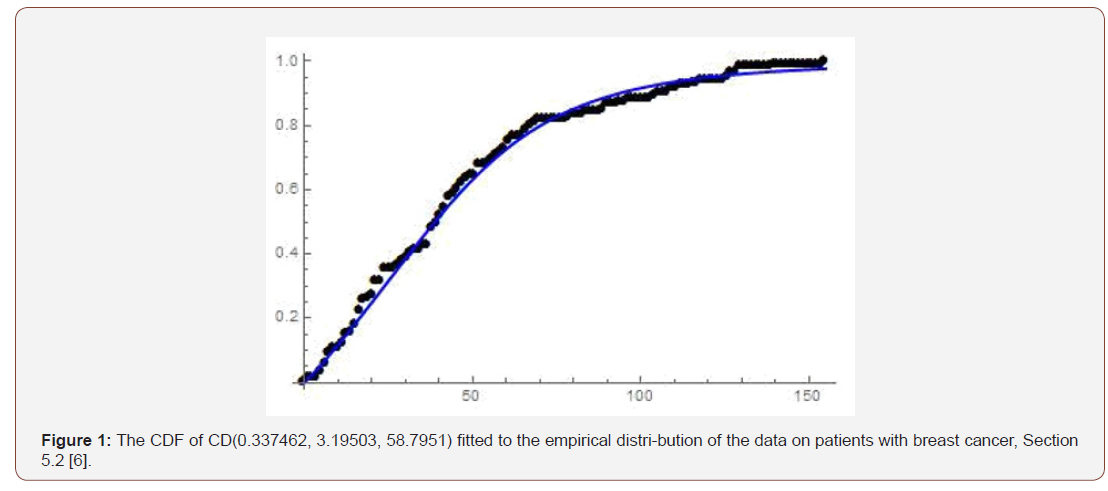
Remark 6.2. The PDF of Cot-Dagum can be obtained by differentiating the CDF. We write S ∼ CD(a, b, c), if S is a Cot-Dagum random variable (Figure 1).
Practical Illustration of Cot Odds T-X
We assume T is a Frechet random variable with CDF
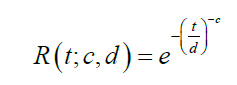
for x, c, d > 0. We also assume that X is a Weibull random variable with CDF given by
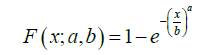
for x, a, b > 0. Now from Section 3, we have the following
Proposition 7.1. The CDF of Cot Odds Frechet-Weibull is given by
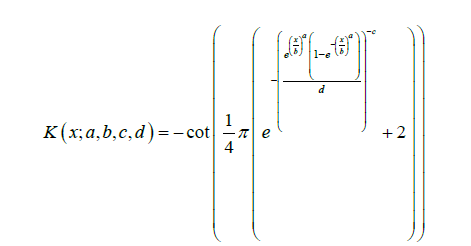
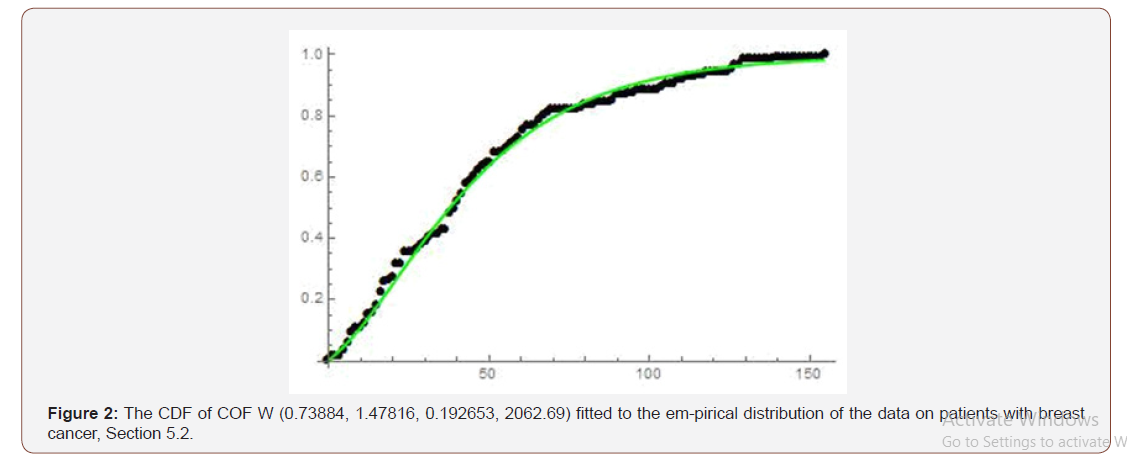
Remark 7.2. The PDF of Cot Odds Frechet-Weibull can be obtained by differentiating the CDF. We write J ∼ COF W (a, b, c, d), if J is a Cot Odds Frechet-Weibull random variable (Figure 2).
Concluding Remarks
In the present paper we introduced the Cot-X and Cot Odds T-X family of distributions respectively and have shown fit to real-life data. The future interesting problem is to investigate some properties and application of these new classes of statistical distributions.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Omid KHARAZMI, Ali SAADATINIK (2016) Hyperbolic Cosine - F Family of Distri-butions with an Application to Exponential Distribution. GU J Sci 29(4): 811-829.
- Omid Kharazmi, Ali Saadatinik, Mostafa Tamandi, A New Continuous Life-time Distribution and its Application to the Indemnity and Aircraft Windshield Datasets. Mathematical Sciences and Applications E-Notes 7(1): 102-112.
- Ahmad Z (2019) The Hyperbolic Sine Rayleigh Distribution with Application to Bladder Cancer Susceptibility. Ann Data Sci 6: 211.
- Kharazmi, O., Saadatinik, A. & Jahangard, S (2019) Odd Hyperbolic Cosine Exponential-Exponential (OHC-EE) Distribution Ann Data Sci: 1–21.
- Ayman Alzaatreh, Carl Lee, Felix Famoye (2013) A new method for generating families of continuous distributions. METRON 71: 63-79.
- Girish Babu Moolath, Jayakumar K (2017) T-Transmuted X Family of Distributions, STA-TISTICA, anno LXXVII, n. 3.
-
Clement Boateng Ampadu. The Cot-X Family of Distributions with Application. Annal Biostat & Biomed Appli. 3(1): 2019. ABBA. MS.ID.000551.
Trigonometric functions; Statistical distributions; Breast cancer; Odds T-X Contents
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






