 Mini Review
Mini Review
Shiga Toxin and Shiga–Like Toxin (SLT) Time-Resolved Absorption and Resonance FT–IR and Raman Biospectroscopy and Density Functional Theory (DFT) Investigation of Vibronic–Mode Coupling Structure in Vibrational Spectra Analysis
Alireza Heidari1*, Jennifer Esposito2 and Angela Caissutti2
1Faculty of Chemistry, California South University, USA
2American International Standards Institute, USA
Alireza Heidari, Faculty of Chemistry, California South University, USA.
Received Date: April 04, 2019; Published Date: May 23, 2019
Abstract
Shiga toxins are a family of related toxins with two major groups, Stx1 and Stx2, expressed by genes considered to be part of the genome of lambdoid prophages. The toxins are named after Kiyoshi Shiga, who first described the bacterial origin of dysentery caused by Shigella dysenteriae. Shiga–like toxin (SLT) is a historical term for similar or identical toxins produced by Escherichia coli [1-3]. The most common sources for Shiga toxin are the bacteria S. Dysenteriae and some serotypes of Escherichia coli (STEC), which includes serotypes O157:H7, and O104:H4. Parameters such as FT–IR and Raman vibrational wavelengths and intensities for single crystal Shiga Toxin and Shiga–Like Toxin (SLT) are calculated using density functional theory and were compared with empirical results. The investigation about vibrational spectrum of cycle dimers in crystal with carboxyl groups from each molecule of acid was shown that it leads to create Hydrogen bounds for adjacent molecules. The current study aimed to investigate the possibility of simulating the empirical values. Analysis of vibrational spectrum of Shiga Toxin and Shiga–Like Toxin (SLT) is performed based on theoretical simulation and FT–IR empirical spectrum and Raman empirical spectrum using density functional theory in levels of F/6– 31G*, HF/6–31++G**, MP2/6–31G, MP2/6– 31++G**, BLYP/6–31G, BLYP/6–31++G**, B3LYP/6–31G and B3LYP6–31–HEG**. Vibration modes of methylene, carboxyl acid and phenyl cycle are separately investigated. The obtained values confirm high accuracy and validity of results obtained from calculations.
Keywords: Vibronic structure; Vibrational spectra analysis; Density functional theory; Shiga toxin and shiga like toxin; Non-focal functions of becke; Correlation functions of lee-yang-parr; Time–resolved absorption and resonance; FT–IR and raman biospectroscopy
Introduction
Shiga toxins are a family of related toxins with two major groups, Stx1 and Stx2, expressed by genes considered to be part of the genome of lambdoid prophages. The toxins are named after Kiyoshi Shiga, who first described the bacterial origin of dysentery caused by Shigella Dysenteriae. Shiga–like toxin (SLT) is a historical term for similar or identical toxins produced by Escherichia coli [1-3]. The most common sources for Shiga toxin are the bacteria S. Dysenteriae and some serotypes of Escherichia coli (STEC), which includes serotypes O157:H7, and O104:H4. Density Functional Theory (DFT) is one of the most powerful calculation methods for electronic structures [5-7]. Numerous results have been previously studied and indicate successful use of these methods [8-10]. The theory is one of the most appropriate methods for simulating the vibrational wavenumbers, molecular structure as well as total energy. It may be useful to initially consider the calculated results by density functional theory using F/6–31G*, HF/6–31++G**, MP2/6–31G, MP2/6–31++G**, BLYP/6–31G, BLYP/6–31++G**, B3LYP/6–31G and B3LYP6–31–HEG** approach [11-16]. It should be noted that calculations are performed by considering one degree of quantum interference as well as polarization effects of 2d orbitals in interaction [17].
Details of Calculations
All calculations of molecular orbital in the base of ab are performed by Gaussian 09. In calculation process, the structure of Shiga Toxin and Shiga–Like Toxin (SLT) molecule (Figure 1) is optimized and FT–IR and Raman wavenumbers are calculated using F/6–31G*, HF/6– 31++G**, MP2/6–31G, MP2/6–31++G**, BLYP/6–31G, BLYP/6–31++G**, B3LYP/6–31G and B3LYP6–31– HEG** base. All optimized structures are adjusted with minimum energy. Harmonic vibrational wavenumbers are calculated using second degree of derivation to adjust convergence on potential surface as good as possible and to evaluate vibrational energies at zero point. In optimized structures considered in the current study, virtual frequency modes are not observed which indicates that the minimum potential energy surface is correctly chosen. The optimized geometry is calculated by minimizing the energy relative to all geometrical quantities without forcing any constraint on molecular symmetry. Calculations were performed by Gaussian 09. The current calculation is aimed to maximize structural optimization using density functional theory. The calculations of density functional theory is performed by F/6–31G*, HF/6– 31++G**, MP2/6–31G, MP2/6–31++G**, BLYP/6–31G, BLYP/6– 31++G**, B3LYP/6– 31G and B3LYP6–31–HEG** function in which non–focal functions of Becke and correlation functions of Lee–Yang–Parr beyond the Franck–Condon approximation are used. After completion of optimization process, the second order derivation of energy is calculated as a function of core coordination and is investigated to evaluate whether the structure is accurately minimized. Vibrational frequencies used to simulate spectrums presented in the current study are derived from these second order derivatives. All calculations are performed for room temperature of 411 (K) (Figure 1).
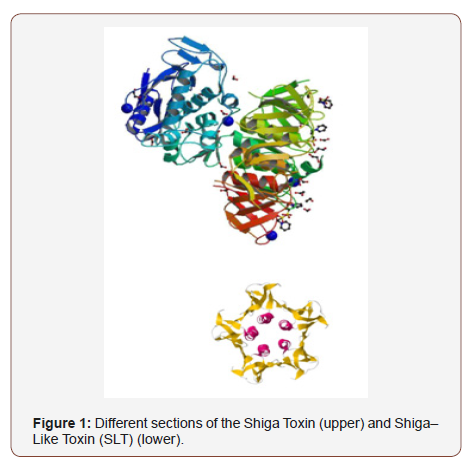
Vibration Analysis
Analysis of vibrational spectrum of Shiga Toxin and Shiga–Like Toxin (SLT) is performed based on theoretical simulation and FT–IR empirical spectrum and Raman empirical spectrum using density functional theory in levels of F/6–31G*, HF/6–31++G**, MP2/6– 31G, MP2/6–31++G**, BLYP/6–31G, BLYP/6–31++G**, B3LYP/6– 31G and B3LYP6–31–HEG**. Vibration modes of methylene, carboxyl acid and phenyl cycle are separately investigated. C–H stretching vibrations in single replacement of benzene cycles are usually seen in band range of 3100–3350 cm–1. Weak Raman bands are at 3089 cm–1 and 3102 cm–1. C–C stretching mode is a strong Raman mode at 1099 cm–1. Raman weak band is seen at 1573 cm–1 too. Bending mode of C–H is emerged as a weak mode at 1388 cm–1 and 1187 cm–1 and a strong band at 1271 cm–1 in Raman spectrum. Raman is considerably active in the range of 1100–1350 cm–1 which 1093 cm–1 indicates this issue.
C–H skew–symmetric stretching mode of methylene group is expected at 3085 cm–1 and its symmetric mode is expected at 2899 cm–1. Skew–symmetric stretching mode of CH2 in Shiga Toxin and Shiga–Like Toxin (SLT) has a mode in mid–range of Raman spectrum at 3000–3120 cm–1. When this mode is symmetric, it is at 2995 cm–1 and is sharp. The calculated wavenumbers of higher modes are at 2963 cm–1 and 2993 cm–1 for symmetric and skew–symmetric stretching mode of methylene, respectively. Scissoring vibrations of CH2 are usually seen at the range of 1427–1481 cm–1 which often includes mid–range bands. Weak bands at 1440 cm–1 are scissoring modes of CH2 in Raman spectrum. Moving vibrations of methylene are usually seen at 1369 cm–1 for the investigated chemical in the current study, these vibrations are at 1239 cm–1 were calculated using density functional theory. Twisting and rocking vibrations of CH2 are seen in Raman spectrum at 815 cm–1 and 1089 cm–1, respectively, which are in good accordance with the results at 799 cm–1 and 1064 cm–1, respectively.
In a non–ionized carboxyl group (COOH), stretching vibrations of carbonyl [C=O] are mainly observed at the range of 1740–1788 cm–1. If dimer is considered as an intact constituent, two stretching vibrations of carbonyl for symmetric stretching are at 1640–1685 cm–1 in Raman spectrum. In the current paper, stretching vibration of carbonyl mode is at 1697 cm–1 which is a mid–range value. Stretching and bending bands of hydroxyl can be identified by width and band intensity which in turn is dependent on bond length of Hydrogen. In dimer form of Hydrogen bond, stretching band of O–H is of a strong Raman peak at 1267cm–1 which is due to in–plain metamorphosis mode. Out–of–plain mode of O–H group is a very strong mode of peak at 949cm–1 of Raman spectrum. The stretching mode of C–O (H) emerges as a mid–band of Raman spectrum at 1147cm–1.
Lattice vibrations are usually seen at the range of 0–450cm–1. These modes are induced by rotary and transferring vibrations of molecules and vibrations and are including Hydrogen bond. Bands with low wavenumbers of Hydrogen bond vibrations in FT–IR and Raman spectrum (Figure 2) are frequently weak, width and unsymmetrical. Rotary lattice vibrations are frequently stronger than transferring ones. Intra–molecular vibrations with low wavenumbers involving two–bands O–H …O dimer at 78 cm– 1, 93 cm–1 and 149 cm–1 are attributed to a rotary moving of two molecules involving in–plain rotation of molecules against each other (Figure 2)
Conclusion and Summary
Calculations of density functional theory using F/6–31G*, HF/6– 31++G**, MP2/6–31G, MP2/6–31++G**, BLYP/6–31G, BLYP/6– 31++G**, B3LYP/6–31G and B3LYP6–31–HEG** levels were used to obtain vibrational wavenumbers and intensities in single crystal of Shiga Toxin and Shiga–Like Toxin (SLT). Investigation and consideration of vibrational spectrum confirm the formation of dimer cycles in the investigated crystal with carboxyl groups from each Hydrogen molecule of acid protected from adjacent molecules. The calculated vibrational spectrum which obtains from calculations of density functional theory is in good accordance with recorded empirical values which indicates successful simulation of the problem. The obtained results indicate that the results obtained from theoretical calculations are valid through comparing with empirical recorded results.
Acknowledgement
Authors are supported by an American International Standards Institute (AISI) Future Fellowship Grant FT1201009373497. We acknowledge Ms. Isabelle Villena for instrumental support and Dr. Michael N. Cocchi for constructing graphical abstract figure. We gratefully acknowledge Prof. Dr. Christopher Brown for proofreading the manuscript.
Conflict of interest
No conflict of interest.
References
- Yu P, Wu J, Liu S, Xiong J, Jagadish C, et al. (2016) Design and Fabrication of Silicon Nanowires towards Efficient Solar Cells. Nano Today 11(6): 704-737.
- Sandhu S, Fan S (2015) Current-Voltage Enhancement of a Single Coaxial Nanowire Solar Cell. ACS Photonics 2: 1698-1704.
- Van Dam D, Van Hoof NJJ, Cui Y, Van Veldhoven PJ, Bakkers EPAM, et al. (2016) High-Efficiency Nanowire Solar Cells with Omnidirectionally Enhanced Absorption Due to Self-Aligned Indium-Tin-Oxide Mie Scatterers. ACS Nano 10: 11414-11419.
- Luo S, Yu WB, He Y, Ouyang G (2015) Size-Dependent Optical Absorption Modulation of Si/Ge and Ge/Si Core/shell Nanowires with Different Cross-Sectional Geometries. Nanotechnology 26(8): 085702.
- Yu P, Yao Y, Wu J, Niu X, Rogach AL, et al. (2017) Effects of Plasmonic Metal Core-Dielectric Shell Nanoparticles on the Broadband Light Absorption Enhancement in Thin Film Solar Cells. Sci Rep 7: 7696.
- Gouda AM, Allam NK, Swillam MA (2017) Efficient Fabrication Methodology of Wide-angle Black Silicon for Energy Harvesting Applications. RSC Adv 7: 26974-26982.
- Branz HM, Yost VE, Ward S, Jones KM, To B, et al. (2009) Nanostructured Black Silicon and the Optical Reflectance of Graded-Density Surfaces. Appl Phys Lett 94: 231121.
- Fazio B, Artoni P, Antonía Iatí M, D’Andrea C, Lo Faro MJ, et al. (2016) Strongly Enhanced Light Trapping in a Two-Dimensional Silicon Nanowire Random Fractal Array. Light Sci Appl 5: e16062.
- Ko MD, Rim T, Kim K, Meyyappan M, Baek CK (2015) High Efficiency Silicon Solar Cell Based on Asymmetric Nanowire. Sci. Rep 5: 11646.
- Oh J, Yuan HC, Branz HM (2012) An 18.2%-Efficient Black-Silicon Solar Cell Achieved through Control of Carrier Recombination in Nanostructures. Nat Nanotechnol 7: 743-748.
- Lin H, Xiu F, Fang M, Yip S, Cheung HY, et al. (2014) Rational Design of Inverted Nanopencil Arrays for Cost-Effective, Broadband, and Omnidirectional Light Harvesting. ACS Nano 8: 3752-3760.
- Garnett E, Yang P (2010) Light Trapping in Silicon Nanowire Solar Cells. Nano Lett 10: 1082-1087.
- Misra S, Yu L, Foldyna M, Roca I Cabarrocas P (2013) High Efficiency and Stable Hydrogenated Amorphous Silicon Radial Junction Solar Cells Built on VLS-Grown Silicon Nanowires. Sol Energy Mater Sol Cells 118: 90-95.
- Kelzenberg MD, Boettcher SW, Petykiewicz JA, Turner-Evans DB, Putnam MC, et al. (2010) Enhanced Absorption and Carrier Collection in Si Wire Arrays for Photovoltaic Applications. Nat Mater 9: 239-244.
- Tian B, Zheng X, Kempa TJ, Fang Y, Yu N, et al. (2007) Coaxial Silicon Nanowires as Solar Cells and Nanoelectronic Power Sources. Nature 449: 885-889.
- Razek SA, Swillam MA, Allam NK (2014) Vertically Aligned Crystalline Silicon Nanowires with Controlled Diameters for Energy Conversion Applications: Experimental and Theoretical Insights. J Appl Phys 115: 194305.
- Dhindsa N, Walia J, Saini SS (2016) A Platform for Colorful Solar Cells with Enhanced Absorption. Nanotechnology 27: 495203.
-
Alireza Heidari, Jennifer Esposito, Angela Caissutti. Shiga Toxin and Shiga–Like Toxin (SLT) Time-Resolved Absorption and Resonance FT–IR and Raman Biospectroscopy and Density Functional Theory (DFT) Investigation of Vibronic–Mode Coupling Structure in Vibrational Spectra Analysis AnnalBiostat & Biomed Appli. 2(3): 2019. ABBA.MS.ID.000537.
Vibronic structure; Vibrational spectra analysis; Density functional theory; Shiga toxin and shiga like toxin; Non-focal functions of becke; Correlation functions of lee-yang-parr; Time–resolved absorption and resonance; FT–IR and raman biospectroscopy
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






