 Review Article
Review Article
General Fifth M-Zagreb Indices and General Fifth M-Zagreb Polynomials of Dyck-56 Network
Fozia Bashir Farooq*
Department of Mathematics, Al-Imam Mohammad Ibn Saud Islamic University, Riyadh, Saudi Arabia
Fozia Bashir Farooq, Department of Mathematics, Al- Imam Mohammad Ibn Saud Islamic University, Riyadh, Saudi Arabia.
Received Date: August 31, 2021; Published Date: September 23, 2021
Abstract
A topological index is a type of molecular index that is calculated from the molecular graph of chemical structure. A topological index relates chemical structure with its underlying physical, biological and chemical properties. This article deals with General fifth M1 and General fifth M2– Zagreb indices and General fifth M1 and general fifth M2–Zagreb polynomials of Dyck-56𝑛×𝑛 network.
Keywords: Dyck-56 Network; Zagreb index; Zagreb polynomial
Introduction
A chemical graph can be represented by polynomial, a numerical value or a matrix form. Topological indices are major source of the relationship between physical and biological properties and behavior of chemical structures. Topological indices are used in development quantitative structure activity relationships in which properties of molecules are correlated with their chemical structure. Let 𝐺(𝑉, 𝐸) be a graph with vertex set 𝑉 and edge set 𝐸, with |𝑉| = 𝑚 and |𝐸| = 𝑛. Let 𝑑𝑢 represent the degree of a vertex 𝑢 in graph 𝐺. 𝑆𝑢 stands for sum of degrees of the vertices incident with vertex 𝑢 in 𝐺. Milan Randic [1] introduced the first degree-based Topological index, i.e Randic Index, Defined as;
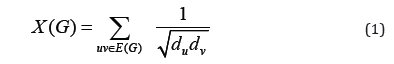
Furthermore, Bollabas and Erdos [2] introduced general Randic index as;
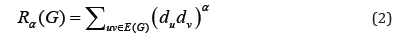
Gutman and Trinajstic [3] introduced first and second Zagreb indices as;
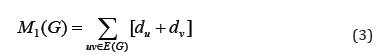

Recently in [4], Kulli introduced new indices that are general fifth 𝑀1- Zagreb indices denoted by 𝑀1 𝛼𝐺5(𝐺) and general fifth 𝑀2- Zagreb indices denoted by 𝑀2 𝛼𝐺5(𝐺) defined as;
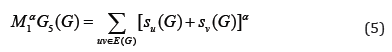
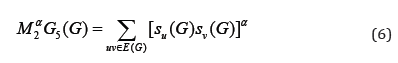
The general fifth 𝑀1- Zagreb polynomial denoted by 𝑀1𝛼𝐺5(𝐺, 𝑥) and general fifth 𝑀2- Zagreb polynomial denoted by 𝑀𝛼2𝐺5(𝐺, 𝑥) is defined as;
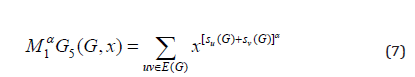
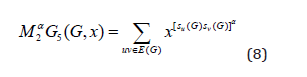
Dyck-56𝑛×𝑛 Networks were built up by unit representation of Dyck−56 (Dyck 1880) by identification procedure. Further detail about formation of Dyck Network can be found in [5]. Dyck graph is the 3-regular graph with 32 vertices and 48 edges, having chromatic number 2 and chromatic index 3 with diameter 5. Further details of formation of Dyck- 56𝑛×𝑛 network can be found in [5,6]. Selvan and Naranyakar in [7] calculated general Randic Index, First Zagreb index, ABC and GA indices for Dyck-x, ABC and GA indices for Dyck-56𝑛×𝑛 network.
Main Results
Figure 1 Dyck-56𝑛×𝑛(𝐴) Network has 12𝑛2 + 4𝑛 vertices and 18𝑛2 − 2𝑛 edges. Based on the sum of the degrees of incident vertices to the end vertices of each edge, there are seven types of edges of Dyck-56𝑛×𝑛(𝐴) Network. This edge partition is presented in (Table 1) [8-10].
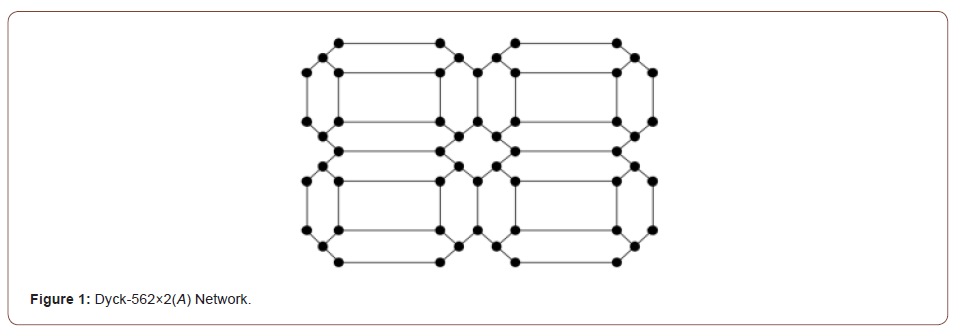
Table 1: Edge Partition of Dyck-56𝑛×𝑛(A) Network.
Theorem 1: Let 𝐺 be the graph Dyck-56𝑛×𝑛(𝐴) Network, and the general fifth 𝑀1- Zagreb index for 𝐺 is
Proof. Let 𝐺: = Dyck-56𝑛×𝑛(𝐴) Network; the above result can be found by using Table 1 and equation 5.
So,
Which further reduces to
Theorem 2: Let 𝐺 be the graph Dyck-56𝑛×𝑛(𝐴) Network, and the general fifth 𝑀2- Zagreb index for 𝐺 is
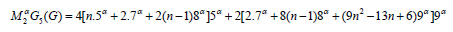
Proof. Let 𝐺 be Dyck-56𝑛×𝑛(𝐴) Network. The above result can be found using (Table 1) and equation 6.
So,
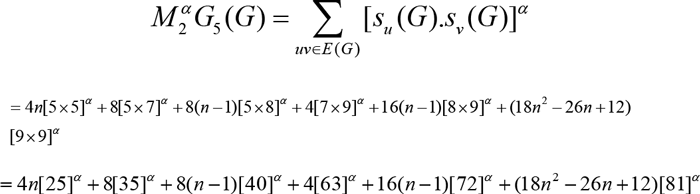
Which further reduces to
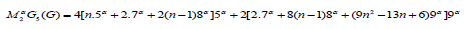
Theorem 3: Let 𝐺 be the graph Dyck-56𝑛×𝑛(𝐴) Network, and the general fifth 𝑀1- Zagreb polynomial for 𝐺 is [
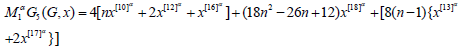
Proof. Let 𝐺 be Dyck-56𝑛×𝑛(𝐴) Network. The above result can be found using (Table 1) and equation 7.
So,
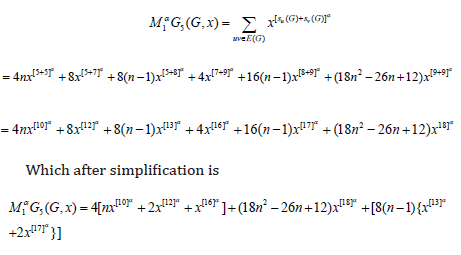
Theorem 4: Let 𝐺 be the graph Dyck-56𝑛×𝑛(𝐴) Network, The general fifth 𝑀2- Zagreb polynomial for 𝐺 is
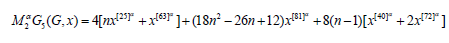
Proof. Let 𝐺 be Dyck-56𝑛×𝑛(𝐴) Network. The above result can be found by using (Table 1) and equation 7.
So,
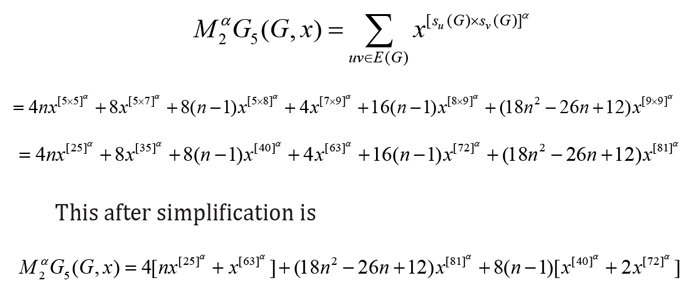
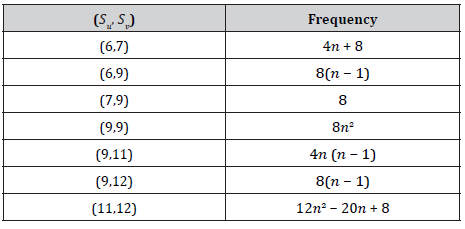
Figure 2 Dyck-56𝑛×𝑛(𝐵) Network has 18𝑛2 − 3𝑛 vertices and 24𝑛2 − 4𝑛 + 8 edges. On the base of sum of degrees of incident vertices to end vertices of each edge there are seven types of edges of Dyck-56𝑛×𝑛(𝐵) Network. This edge partition is given in (Table 2) [11-13].
Theorem 5: Let 𝐺 be the graph Dyck-56𝑛×𝑛(𝐵) Network, The general fifth 𝑀1- Zegreb index for G is
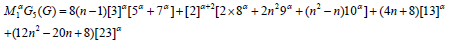
Proof. Let 𝐺 be Dyck-56𝑛×𝑛(𝐴) Network, The above result can be found by using (Table 1) and equation 5.
So,
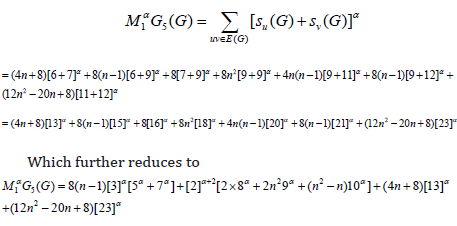
Theorem 6: Let G be the graph Dyck-56𝑛×𝑛(𝐵) Network. The general fifth 𝑀2- Zegreb index for G is
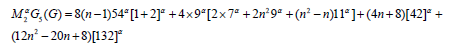
Proof. Let 𝐺 denotes Dyck-56𝑛×𝑛(𝐵) Network. The above result can be found by using (Table 2) and equation 6.
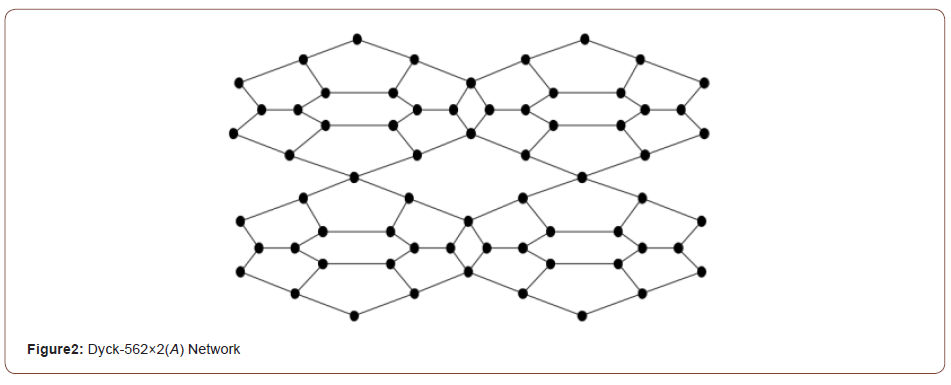
Table 2: Edge Partition of Dyck-56𝑛×𝑛(B) Network.
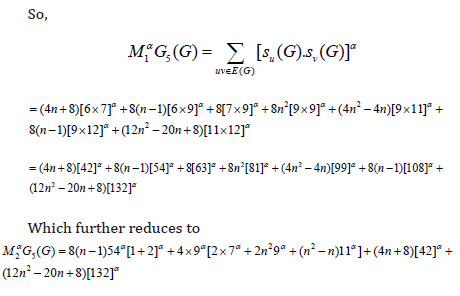
Theorem 7: Let 𝐺 be the graph Dyck-56𝑛×𝑛(𝐵) Network, The general fifth 𝑀1- Zagreb polynomial for 𝐺 is
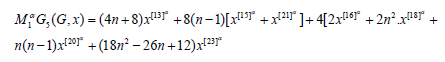
Proof. Let 𝐺 is Dyck-56𝑛×𝑛(𝐵) Network, The above result can be found by using (Table 2) and equation 7. So,
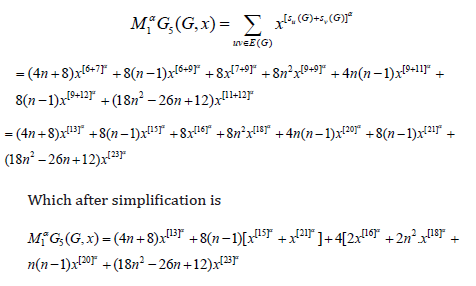
Theorem 8: Let G be the graph Dyck-56𝑛×𝑛(𝐵) Network, The general fifth 𝑀2- Zegreb polynomial for G is
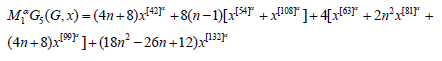
Proof. Let 𝐺 be Dyck-56𝑛×𝑛(𝐵) Network. The above result can be found by using (Table 2) and equation 8.
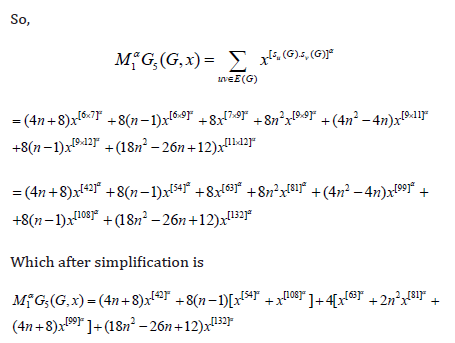
Conclusion
Degree based topological indices like General fifth M1 and General fifth M2 Zagreb indices for Dyck-56 Network are found in this paper. These indices are useful in study of QSAR/QSPR. Furthermore, General fifth M1 and General fifth M2-Zagreb polynomials for Dyck-56 Networks are found. These indices and polynomials are useful for the study to understand correlation between physical structures with chemical properties.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Randic M (1975) On Characterization of molecular branching. J Am Chem Soc 97: 6609–6615.
- A Graovac, M Ghorbani, MA Hosseinzadeh (2011) Computing _fth geometric- arithmetic index of nanostar dendrimers. Journal of Mathematical Nanoscience1(1): 33-42.
- Bollobás, B, Erdös P (1998) Graphs of extermal weights. Ars Comb 50: 225-233.
- Gutman I, Trinajstic N (1972) Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem Phys Lett 17(4): 535-538.
- MV Diudea, Cs L Nagy (2013) Diamond and related Nanostructures, Springer.
- Mircea V Diudea, Katalin Nagy, Monica L Pop, F Gholami Nezhaad, AR Ashrafi (2010) Omega and PIv Polynomial in Dyck Graph-like Z(8)-Unit Networks. Int J Nanosci Nanotechnol 6(2): 97-103.
- D Selwan, KP Prayankar (2020) On Topological Properties of Dyck-56 Networks. International Journal of Applied Graph Theory 4(1): 1-15.
- VR Kulli (2017) General Fifth M-Zagreb Indices and Fifth M-Zagreb Polynomials of PAMAM Dendrimers. Intern J Fuzzy Mathematical Archive 13(1): 99-103.
- Munir M, Nazeer W, Rafique S, Kang S (2016) M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry 8:149.
- Gao W, Wang W, Farahani MR (2016) Topological indices study of molecular structure in anticancer drugs. J Chem.
- Hayat S, Imran M (2015) On degree based topological indices of certain nanotubes. J Comput Nanosci 12: 1599-1605.
- Yang H, Rashid MA, Ahmad S, Khan SS, Siddiqui MK (2019) On molecular descriptors of face-centered cubic lattice. Processes 7: 280.
- DH Rouvray (1987) The modeling of chemical phenomena using topological indices. Journal of computational chemistry 8: 470.
-
Fozia Bashir Farooq. General Fifth M-Zagreb Indices and General Fifth M-Zagreb Polynomials of Dyck-56 Network. Annal Biostat & Biomed Appli. 4(4): 2021. ABBA.MS.ID.000591. DOI: 10.33552/ABBA.2021.04.000591.
Dyck-56 Network, Zagreb index, Zagreb polynomial, Matrix, Topological indices, Vertices, Chemical structures
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






