 Research Article
Research Article
Utilizing a Poissonian count variable Model, with a Second Order Eigen-Autocorrelation and a Hierarchical Bayesian Non-Frequentist Model to Forecast Hot-Spots of Potential Cases of Ewing Sarcoma in Hispanic Males in Hillsborough County, Florida, USA
Clayton Moeller1*, Namit Choudhari2, Caleb Jaramillo3, Aarya Satardekar3, Nada Flaifl3, Sasha Mosich3, and Benjamin Jacob3
1Department of Chemistry, College of Arts and Sciences, University of South Florida, United States of America
2School of Geosciences, University of South Florida, United States of America
3Department of Global Health, College of Public Health, University of South Florida, United States of America
Clayton Moeller, Department of Chemistry, College of Arts and Sciences, University of South Florida, United States of America
Received Date: September 09, 2025; Published Date: September 15, 2025
Abstract
Ewing Sarcoma (ES) is one of the most aggressive bone and soft tissue sarcomas. ES primarily targets more vulnerable populations primarily between the ages of 10-15 years old. Regretfully, this cancer also has no current method of prediction. ES is a small, blue, round cell sarcoma that typically occurs with the gene transfusion of the EWSR1-FLI1 genes across chromosomes #11-#22(~85-90%). Studies acquired in literature show an increasing presence of ES as well as a tendency for higher rate of metastasis amongst adolescent (<20 years), Hispanic males. While Florida is not a part of Surveillance, Epidemiology, and End Results (SEER) data, prior US studies have shown vulnerability to those of lower Socio-Economic Status. Initially this study conducted population stratification, using data gathered from Dhir et al., 2024 and the United States Census Bureau to determine a population stratified prevalence. We created a map based on hot and cold spots of vulnerability at the zip code level in Hillsborough County, Florida. Thereafter, we developed a Poisson probability model based on socio-demographic co-variants for ES. Subsequently, a second order autocorrelation and Bayesian model was employed to eigen-decompose the socio-demographic variants. In doing so, we were able to predictively map potential hot and cold spots which allowed determination of causation co-variants for ES at the zip code level in Hillsborough County, Florida.
Keywords:Ewing sarcoma; hispanic; poisson; bayesian; hillsborough county; florida
Introduction
Ewing Sarcoma (ES) is classified as a rare cancer type that attacks osseous and osseous surrounding tissues in an aggressive manner. While most cancers can be linked to a genetic predisposition or environmental factor causing genetic mutation, ES has no common predictive modeling capabilities, except for a disruption in gene expression [1]. The translocation of the mutated gene, EWS-FLI-1, transpires from chromosome #11and #22. While the cause for DNA disruption is still unknown, a prevalence in lower socio-economic demographics suggests that it could be an environmental factor. Current literature suggests that at time of diagnosis, approximately 20% of cases have metastasized. The current survival rate of ES is approximately 20-30% [1]. Even more concerning is the fact that the lowest survival rates come from those with limited access to proper triage and care. Currently the treatment costs for chemotherapy can vary anywhere from $11,162.86 to $46,926.00 per treatment per month [2]. This extreme price gap makes such crucial treatment unaffordable for many low income and uninsured patients, especially those that require radiation and surgery. A recent study examines a potential link found between those with a potential higher co-morbidity rate and lower socioeconomic status [3].
This high co-morbidity could be attributable to the lack of access to proper timely screening for those with a lower mean income and those living in rural conditions, when compared to those living in an urban or metropolitan environment. The factors of expensive and more limited care, coupled with a directed prevalence at more vulnerable populations, (i.e., lower income, adolescence, and racial demographic profiles), prioritizes the need for early diagnosis. An issue arises when considering the accessibility of care and cost of early identification vulnerabilities. Unfortunately, victims of ES may not realize that they are at risk until they have malignant symptoms, (i.e., a lump along a weight bearing joint/thorax, excessive fatigue, etc.). If there is a suspected genetic mutation, an oncologist may suggest genomic testing, which typically costs anywhere from $300-$10,000 [4]. ES is so rare that many care centers may not be able to diagnosis or treat this cancer in a timely fashion due to a lack of awareness or information available. Misdiagnosis, extreme pricing of tests and the inability to properly locate those potentially impacted are all key co-factors that can increase the prevalence of ES. In this paper we generated multiple probability models to determine geographical locations for prioritization of ES prevention and treatment.
We employed a count variable Poisson model to quantify land use land cover (LULC) and socio demographic co-variants associated with ES. We initially employed literature and census data to create a population stratification for the entire county of Hillsborough, which included all 55 zip codes. This study employed the known incidence of cases of ES in adolescent (<20) Hispanic males in Florida which has a prevalence of 2.05 to every 1 million [5]. We created the conversion of (Potential cases: Population), using the ratio ≈ 3.1/1.5 million. Subsequently we quantified potential cases at the zip code level employing the following equation
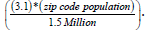
There are currently no predictive epidemiological models for quantifying ES from a socio-economic standpoint. Current literature is restricted to census data and clinical output from oncological studies. Our assumption was that by employing LULC and socio-demographic county zip code level data, we could generate an artificial risk stratification [7] to target potential cases for preemptive screening and greater accessibility to treatment locations. Currently there are no contributions in literature that employ predictive modeling for ES. Therefore our objectives in this research undertaking were 1. To construct a count variable regression model to generate a parameter hierarchy of LULC and socio-demographic covariates 2. To generate georeferenced aggregation/non-aggregation oriented (Hot/Cold spot) autocorrelation map using a second order eigenfunction eigen-decomposition algorithm; and, 3. To develop a probabilistic geospatial Bayesian generalizable hierarchical analysis to localize clustering/non-clustering causation determinants for precision mapping protocols for ES in Hillsborough County Florida.
Methodology
This study employed statistical modeling techniques (Poisson, Second Order-Autocorrelation, and Bayesian), to study the possibility of mapping potential cases of ES in Hillsborough County, Florida. Using census data [8] and data found in literature a, (as Florida is not included in SEER), this study weighed the potential cases, found by utilizing an artificial population stratification as conducted in Satardekar et al., 2024. We used covariates contributed in literature to be significant in the predisposition of contracting ES. The prevalence of ES at the county level; 2.05 cases per 1 million. The risk stratification was quantified using the equation:
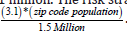
Study site
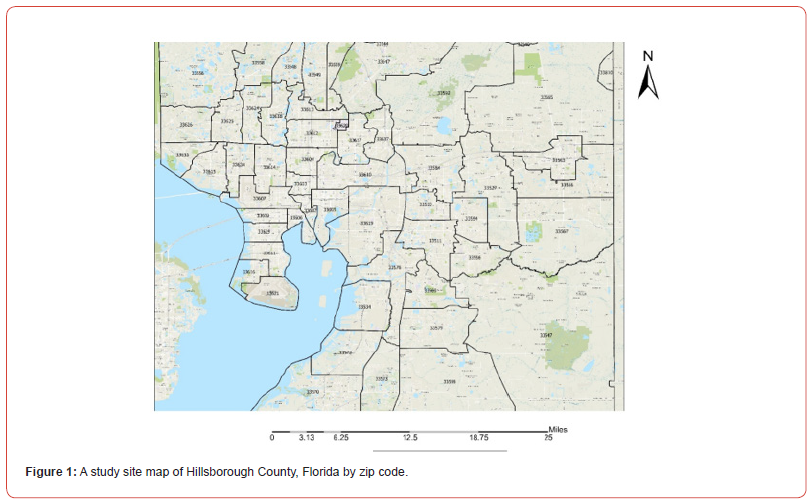
Hillsborough County is the 13th largest county by land in Florida and 2nd largest by total population with approximately 1.5 million residents currently in occupation [8]. Nearly a third of the population is Hispanic or of Hispanic descent putting a large percentage of the population at risk of contracting ES [5,8]. It is a central hub for both culture and economics in Florida. The enriched mix of urban, farmland, and rural land cover makes for a diverse spread of variables to be applied in statistical modeling for ES (Figure 1).
A Poisson regression, with statistical significance, was determined by a 95% confidence level which was employed to ascertain whether the county proportions of sampled sociodemographic and LULC, ES covariates differed by zip codes in the Hillsborough County intervention site. Poisson regression can be used for prediction, inference, hypothesis testing, and modeling of causal relationships among sampled, signature, capture point, county, zip code, stratifiable oncological-related, sociodemographic and LULC covariates [7]. The regression analyses assumed independent counts (i.e.,ni), taken at county zip code locations i = 1 2... n, where each of the signature, capture point, stratified, sampled count value, was derived from a Poisson distribution. These counts were described by a set of explanatory variables denoted by matrix Xi, a 1×p vector of covariate estimates for a sampled georeferenced zip code location i.
The expected value of these data was given by:
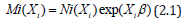
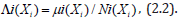
Eigen-Spatial Autocorrelation
An eigenfunction spatial filter eigen-decomposition model specification was also employed to describe the Poisson regressed scalable, sociodemographic and LULC, zip code sampled ES stratified covariates. The resulting model specification took on the following form: Y = ρ (1−ρ )1+ ρWY +ε (2.1) where μ was the scalar conditional mean of Y, and ε was an n-by-1 error vector whose elements were statistically independent and identically distributed (i.i.d) normally random, sampled, capture point zip code stratified ES covariates. The spatial covariance matrix for equation (2.3), using the sampled covariates was
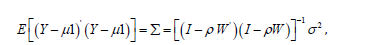
where E(•) denoted the calculus of expectations, I was the n-by-n identity matrix denoting the matrix transpose operation, and σ2 was the error variance.
However, when a mixture of positive and negative eigenspatial autocorrelation is present in a prognosticative, capture point, oncological-related, scalable, zip code model, a more explicit representation of both effects leads to a more accurate interpretation of empirical results [7]. In this experiment, varying, zip code sampled, geospatial autoregressive parameters appeared in the signature ES model specification, which in the model became:
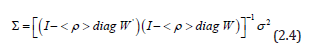
where the diagonal matrix of the regressed sociodemographic and LULC estimator determinants < ρ > diag , contained sampled parameters: ρ + for those covariates pairs displaying positive spatial dependency, and ρ for those pairs displaying negative spatial dependency. By letting σ2 =1 and employing a 2-by-2 regular square tessellation,
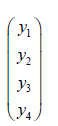
enabled positing a positive relationship between the sampled, county zip code, ES stratified covariates, y1 and y2 , a negative relationship between covariates, y3 and y4 , and, no relationship between covariates y1 an y3 and between y2 and y4 . This covariance specification yielded:
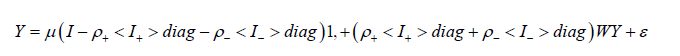
(2.5) where I+ was a binary 0-1 indicator variable which denoted those zip code covariates displaying positive spatial dependency, and I− was a binary 0-1 indicator variable denoting those sampled sociodemographic and LULC zip code data capture points displaying negative spatial dependency, using I−+I− = 1.
If either ρ + = 0 (and hence I+ = 0 and I+ =I) or ρ -= 0 (and hence I- =0 and I+ = 0), then equation (2.5) reduced to equation (2.1). This indicator variables classification was made in accordance with the quadrants of the corresponding Moran scatterplot generated using the sociodemographic and LULC, stratified, ES covariates sampled in the Hillsborough County study site. If positive and negative eigen-spatial autocorrelation processes counterbalance each other in a mixture, the sum of the two autocorrelation parameters-- (ρ++ ρ-) will be close to 0 in an oncological-related, capture point, sociodemographic and LULC, ES prognosticative model [7]. In this experiment the Jacobian estimation was implemented by utilizing the differenced indicator sampled sociodemographic and LULC, stratified prognosticative ES explanatory variables (I+ -Iγ−), which approximated ρ+ and γ with maximum likelihood techniques, and set ρˆ-=−γˆρˆ+. The Jacobian generalizes the gradient of a scalar valued function of multiple variables which itself generalizes the derivative of a scalar-valued function [10].
A more complex model specification was then posited by generalizing the stratified sociodemographic and LULC, capture point, zip code, ES indicator variables. We employed F : Rn → Rm as a function from Euclidean n-space to Euclidean m-space which was generatable in R using the distance between the sampled georeferenced zip code stratified covariates. Such a function was given by m sampled sociodemographic and LULC covariates (i.e., component functions), y1(x1,xn),ym(x1,xn) . The partial derivatives of all these functions were organizable in an m-by-n matrix, the Jacobian matrix J of F, which was illustratable as follows:
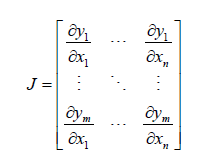
This matrix was denoted by
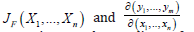
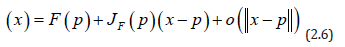
The spatial structuring was achievable by constructing a linearizable combination of a subset of the eigenvectors of a modified geographic weights matrix, using (1−11' / n)C(1−11' / n) that appeared in the numerator of the Moran’s Coefficient (MC). Eigen-spatial autocorrelation can be indexed with a MC, a product moment correlation coefficient [10]. A subset of eigenvectors was then selected with a stepwise regression procedure. Because (1−11' / n)C(1−11' / n) = E Λ E' , where E is an n-by-n matrix of eigenvectors and Λ is an n-by-n diagonal matrix of the corresponding eigenvalues [9], the resulting ES model specification was given by: 1 k Y = μ + Ekβ +ε (2.7) where μ the scalar means of Y, Ek was an n-by-k matrix containing the subset of k << n eigenvectors selected with a stepwise regression technique, and β was a k-by-1 vector of regression coefficients.
Subsequently, a number of eigenvectors were extracted from (1−11' / n)C(1−11' / n) , which were affiliated with geographic patterns of the sampled sociodemographic and LULC, stratified ES covariates, portraying a negligible degree of non-zero eigenspatial autocorrelation. Consequently, only k of the n eigenvectors was of interest for generating a candidate set for a stepwise regression procedure. Candidate eigenvector represents a level of eigen-spatial autocorrelation which can account for the redundant information in eigen-orthogonalized oncological-related, capture point, georeferenceable, hot and cold spot estimated determinant patterns [9]. The preceding eigenvector properties resulted in μˆ = y and ˆβ = EkY for equation (2.6). Expressing equation (2.6) in terms of the preceding 2-by-2 example yielded multiple nonzero eigen-autocorrelated, zip code stratified, capture point, sociodemographic and LULC, ES covariates.
Bayesian estimation procedures
In this experiment, Bayesian regression estimation and Monte Carlo, Markov Chain (MCMC) methods were employed to model the sampled georeferenced, zip code, signature, capture point, ES stratified covariates. In a generalizable Bayesian paradigm, hierarchical models can be used to model heterogeneity of variances on the log-scale [11]. The natural logarithms of variances were modeled using a linear model to account for heterogeneity of the variances (on a logarithmic scale), in terms of the ES stratified, zip code, explanatory, predictor variables sampled. The MCMC sampling began with conditional (marginal) probability distributions, and the georeferenced, capture point, sampled, sociodemographic and LULC, parameter estimators were obtained using pseudo-likelihood estimation (i.e., an autoregressive term approximated with a conventional regression procedure). This involved estimating the sampled coefficients (β ) and ρ as though the census and remote-sampled observations were independent. MCMC outputs can sample values for an parameter drawn from the joint posterior probability distribution [11]. In the first stage of the hierarchal* Bayesian analyses, a likelihood model was specified for the stratified, sampled, ES signature, capture point count data variables.
At the second stage, predictor variables of the sampled sociodemographic and LULC, ES zip code stratified data were analyzed for specifying a prior model. The model recognized conjugate specifications (e.g., Poisson-gamma), from the remote-sampled ES data. Our model assumed that the number of georeferenced, zip code stratified, signature, capture point, sociodemographic and LULC, count data variables in the intervention county study site, Yi, had a conditional independent Poisson distribution with mean Ei exp (μi) . The variable Ei was employed as the expected number of sampling events, which was proportional to the corresponding known zip code, capture point, sampled ES data, ni. The expression exp (μi) was the relative risk based on the estimator determinant, sampled, sociodemographic and LULC, stratified ES capture point, count data values: zip code regions with exp (μi > 1) having greater numbers of observed count values than expected, and vice versa for regions with exp(μi > 1) at the study site.
The log-relative term was μi which modeled all the sampled ES data, linearly as:
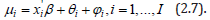
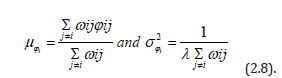
The Monte Carlo method of error propagation assumed that the distribution of error prone variables for each of the input data layers, generated in R derived regressively from the georeferenced, stratified, capture point, sociodemographic and LULC, ES covariates were known. For each of the data layers an error surface was simulated by drawing, at random, from an error pool defined by the geographic distribution of the sampled zip code data capture points. Error surfaces were added to the input data layers and the model was run using the resulting data error layers as input. The process was repeated so that, for each run, a new realization of an error surface was generated for each input data layer. The results of each run were accumulated and a running mean and standard deviation surface for the output was calculable. This process continued until the running mean stabilized. Since the random error visualizations were both positively and negatively non-zero eigen-autocorrelated, the stable running means were taken as the true Gaussian model output surface, and the standard deviation surface was used as a measure of relative error.
A simple summary was generated, showing posterior mean, median and standard deviation, with a 95% posterior credible interval. Models were compared using the Deviance Information Criterion (DIC) in R where DIC = D + pD , was the sum of the posterior mean of the deviance, (D) , a measure of goodness-of-fit, and the effective number of zip code stratified, sociodemographic and LULC, signature, capture point georeferenced sampled parameters (pD). This generated a measure of model complexity. A measure of goodness-of-fit based on the DIC values was applied and an R2DIC , calculated in line with the standard R2 measure for the model. This was definable as: R2DIC = ((DICk−Dbest) / (DICmax-Dbest)) where DICk was the DIC value for model k under evaluation, max DIC was the DIC value for one-fixed parameter model and best D was the posterior deviance from the model.
Results and Discussion
We generated latent, eigen-autocorrelated temporal indices employing the stratified estimator determinants using Moran’s indices (I ) in PySAL. Moran’s, I employed
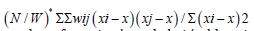
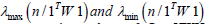
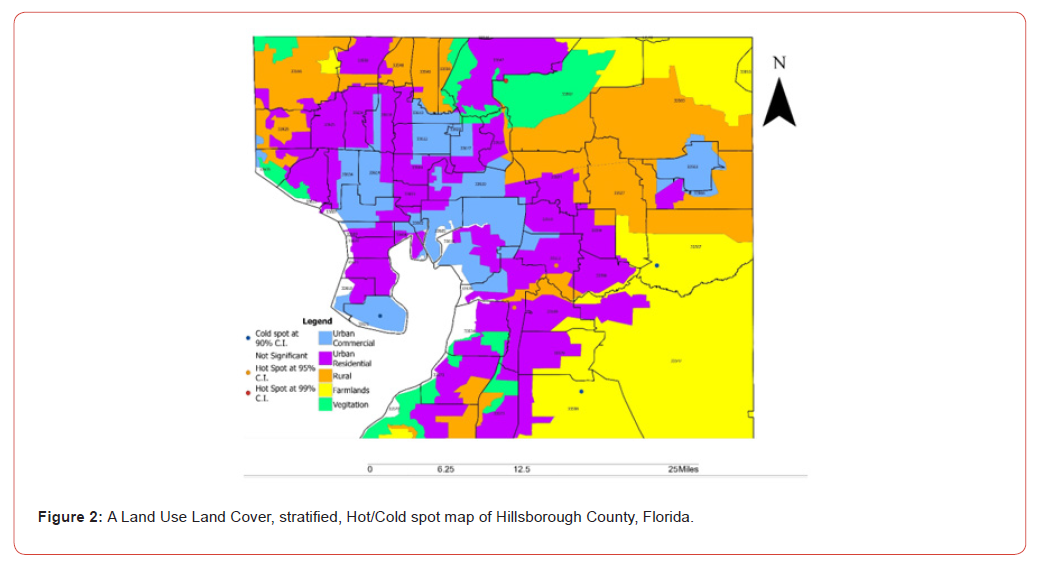
The ES model revealed each georeferenced, county-level, zip code, hot and cold spot which exhibited a distinctive topographic pattern ranging from Positive Spatial Autocorrelation (PSA) (i.e., stratified similar eigen-values of log-transformed, LULC and or sociodemographic, capture point, sampled time series ES data) λi > E(I) to Negative Spatial Autocorrelation (NSA) (i.e., dissimilar log-values clustering in eigen-geospace) for λi > E(I) . Each population stratified, zip code, georeferenced, interpolated, eigendecomposed time series, explanatory estimator determinant, was mapped where E (I )was the expected value of Moran’s I under the assumption of (a) temporal independence and (b) as outputs from related projection matrices M(1) or M( X ) , respectively. We noted that the eigen-decomposed, Moran’s I value of each sampled eigen-filtered, autoregressively forecasted, georeferenced, zip code, hot and cold spot, capture point locations throughout Hillsborough County was robustly interpolatable.
The model output revealed statistically significant georeferenceable LULC and sociodemographic, signature capture point eigenvectors. We noted in the ES model summary diagnostics, each georeferenceable, eigen-decomposed eigenvector was equal to its associated eigenvalue
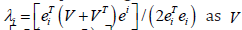
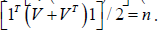
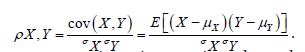
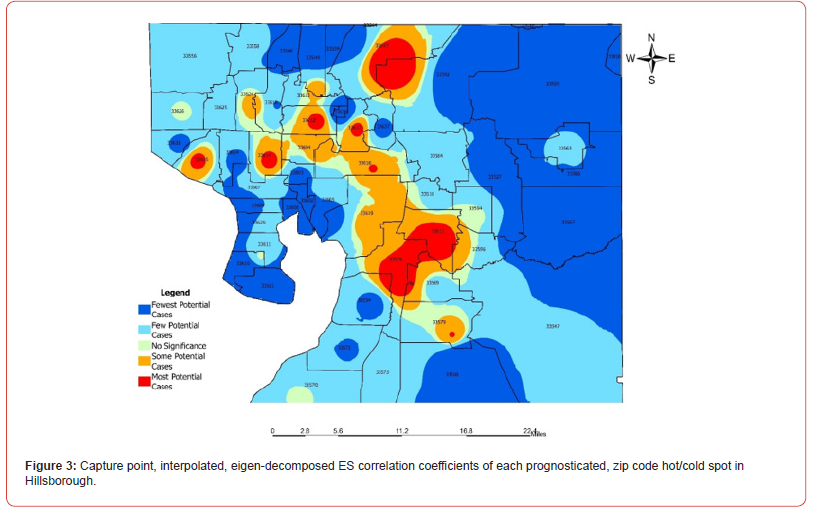
The eigen-model was based on the stratified signature, LULC and sociodemographic, sampled, estimator determinants. For example, during the remote validation exercise we were able to ascertain that many georeferenced eigen-autocorrelated, county, zip code, stratified hot spots of potential ES patients were aggregated in Thonotosassa (zip code 33952). The geospatial pattern in the eigenvectors exhibited only positive local eigen-autocorrelation and vice versa for negative eigen-autocorrelation. The interpolated, time sensitive, stratified, hot/cold spot, signature, scalable, autocorrelated, temporal, Gaussian, oncological-related explanators ei and ej within each set of eigenvectors were mutually non-zero which was revealed using symmetrical transformation 1/2(V +VT) . This was expressible employing a quadratic. The quadratic form representation of the eigen-temporal autocorrelation index [i.e., Moran’s I] captured the non-zero autocorrelation in the interpolation of the zip code, signature, hot/cold spots generated by the ES stratified LULC and sociodemographic signatures.
The eigen-temporal filtered eigenfunction, eigenvectors derived from the georeferenced, stratified, zip code, sampled, hot/cold spot, capture point non-zero autocorrelated estimator determinants were eigen-orthogonal but only to the constant unity vector 1 in X. Eigenvectors corresponding to different eigenvalues will be orthogonal if the matrix is symmetric i.e., real spectral theorem [10]. The second order eigenfunction eigendecomposition allowed linking each collection of the eigenvectors to its specific, georeferenced county, zip code, stratified, sampled capture point, by letting ESAR be a matrix whose vectors were subsets of {e1,..., n}SAR. A higher-order, stratified, autoregressive, capture point model was subsequently constructed in PySAL from the georeferenced, time series, signature, capture point, sampled dataset of county, zip code-level stratified interpolated signature regressors. The model determined where if the lag orders were mis-specified in the sampled, interpolated ES data due to heteroscedastic asymptoticalness.
This violation of regression assumption in the forecasted LULC and sociodemographic, georeferenced, hot/cold spot data, we assumed would be a part of the misspecification bias in the ES sampled modeled estimator determinants which was subsequently correctly specified using a non-asymptotic order. A fixed-effect formula may not remain the same under non-stationarity [12]. A linearized combination of the non-asymptotical, time sensitive, regression coefficient subset was approximated by employing the misspecification term of the signature, capture point, signature interpolated, LULC and sociodemographic, estimator determinant, prognosticated model output which in this experiment was expressible as
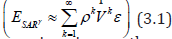
The model
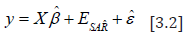
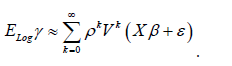
Since ELogγ was uncorrelated with the interpolated, countylevel, stratified, zip code, signatures, X, its incorporation into the georeferenced, scaled-up, sentinel site, vulnerability-oriented model attempted to correct the temporal bias using estimated plain OLS parameters ˆβ. The equation y = Xβˆ + ELogγˆ +εˆ [3.3] revealed the specific, empirical sampled, eigen-valued capture point, estimator determinant variance which in this experiment was retrievable from the eigen-decomposition of the lag signatured, LULC and sociodemographic, population stratified, capture point, model, forecast summary diagnostics. We noted that the trend and the time-series signals were uncorrelated and the MSE was deflated. Euclidean distances between the capture point, temporal, scaled-up, county, zip code aggregation/non-aggregation-oriented, stratified LULC and sociodemographic, ES estimator determinants were definable in terms of an n-by-n geographic weights matrix, C, whose cij values were, 1 if the sampled geolocations i and j were deemed nearby, and 0 otherwise.
Adjusting this matrix by dividing each row entry by its row sum subsequently rendered C1, where 1 was an n-by-1 vector of ones which converted the regression-based matrix to matrix W (i.e., weighted correlation grid).
weighted correlation grid). The resulting autoregressive signature model specification with no sampled, scaled-up, signatured, interpolated, capture point, stratified, ES, estimator determinants (i.e., the pure autoregression specification) subsequently took on the following form: Y = μ (1−ρ )1+ ρWY +ε whereμ was the scalar conditional mean of Y, and ε was an n-by-1 error vector whose LULC or sociodemographic parameters were statistically independently “normalized” random variates. Geospatial signatured, capture point autoregressive models are fit using empirical datasets that contain observations on geographical areas, or on any units with a spatial representation [13]. Approximate standard errors for the stratifiable, county, zip code-level, prognosticative, capture point, estimator determinant model was computable as the square roots of the diagonal elements of the estimated covariance matrix.
The covariance matrix for analyzing the signature oncological, related capture point, time series, stratified estimator determinants was expressible employing
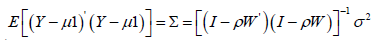
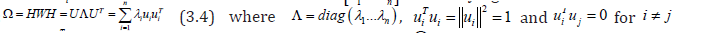
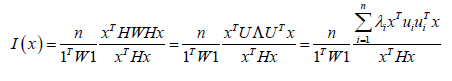
(3.5) Considering the centered vector z = Hx and using the properties of idempotence of H, equation (3.5) was equivalent to:
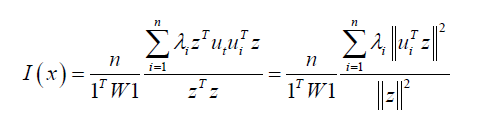
(3.6) As the ES stratified sensitive capture point eigenvectors ui and the vector z were centered, equation (3.6) was rewritten:
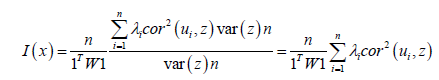
(3.7). In the ES estimator determinant model, r was the number of null eigenvalues of Ω (r ≥ 1). These eigenvalues and corresponding eigenvectors were removed from Λ and U respectively. Equation 3.7 was then strictly equivalent to:
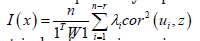
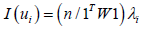
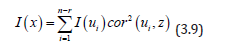
The term cor2(ui,z) represented the part of the variance of z that was explainable by ui in the sampled, time series, dependent, ES, stratified, uncertainty-oriented, capture point, model z = βi ui + ei . This quantity was equal to βi2/n Var (z) . ES estimator determinant decomposed eigenfunction eigenvectors ui were eigen-orthogonal, and therefore, the non-Gaussian homoscedastic regression coefficients of the linear models z = βiui + ei were those of the regression model
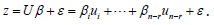
By regressing ES using more evidential independent variables may reveal additional cofactors related to this dysplasia on what could help in developing more focused research. This leads to the second part, which is the lack of early diagnostic power. Staging for cancers is crucial for prognosis and survivability. While there are only three different stages found in literature, which are not universally agreed upon; some say stages 1-3 and others say 2-4 due to severity [1,13]. This continues to prove the volatility of ES and why supplemental research is necessary. In the count variable model, we noted that there was no overdispersion as the VIF was below 10. This may have been due to the low sample count of LULC and socio-demographic variants we used in the Poissonian model. We will attempt to increase variables in future research efforts by using a negative binomial regression with a non-homogeneous gamma-distributed mean. In so doing we would be able to remove outliers from the independent variable dataset while generating and developing a more efficient hierarchy of the co-variants. We employed a second order eigenfunction eigen decomposition algorithm to map hot and cold spots for potential ES caseload. In this experiment we found that Thonotosassa was the hottest spot based on Moran’s I coefficient.
Thonotosassa is a smaller semi-rural community in the Hillsborough County intervention site. We generated a LULC map of this region, which allowed us to distinguish geolocations in Thonotosassa of aggregation sites where <20 White and Hispanic males occurred more frequently. We then constructed a nonfrequentist hierarchical generalizable Bayesian hierarchical model to determine the causation covariates of the hottest capture point in Thonotosassa (33592). We found that the covariate “Population” was the most impactful in the determination of hotspots and prevalence of ES. This is to be expected when considering the relationship between ES, population, and race. Based on the results of the models generated in this research, it may be suggested that as the population or the presence of Caucasian or Hispanic males under 20 increases, so will the number of cases of ES. As Thonotosassa appears as a rural location it may be suggested that there may be a link between lower socio-economic status and the development of ES. Randomly distributed data is to be expected in this situation as the covariates are extremely limited, however this model proved the ability to employ statistical modeling not only in oncology, but in more niche areas of study that are lacking in depth of research.
This issue can be rectified with more in-depth research to discover more regress able covariates as well as utilizing timebased models (e.g., GARCH) in future works to create more accurate prediction times for risk, diagnosis, and staging. This study was designed to illustrate the ability to utilize advanced statistical modeling in ES probability prediction. Georeferencing ES data could prove to be increasingly significant when targeting locations for triage centers for diagnosis and treatment. Unfortunately, rural areas receive less funding than urban centers in Hillsborough County. Due to this bias, there is a necessity to continue to conduct research on ES in rural territories throughout Florida. Precision forecast maps targeting and prioritizing transmission-oriented, diagnostically stratifiable, ES estimator determinants associated with a subcounty, transmission-related, hot /cold spot may require disturbance-free regressors. (e.g., non-Gaussian error variance) for asymptotically optimally reflecting the geo-spatiotemporally of hierarchical, diffusion-related sampled ES determinants. Statistical error or uncertainty is the amount by which an observation differs from its expected value [14], the latter being based on the entire population from which the statistical unit was chosen randomly.
The expected value, being the mean of the entire population, may be typically unobservable in an empirical, non-asymptotical, vulnerability-oriented, geo-spatiotemporal dependent, ES, hierarchical diffusion-related, subcounty, prognosticative model, and hence the statistical error may not be observable. A residual (or fitting deviation), on the other hand, may reveal an observable estimate of the unobservable statistical error, which may be embedded in noisy non-normal trajectories in empirically regressed georeferenced datasets of district-level, sub-county, diagnostically, stratifiable, geo-spatiotemporal, hierarchical, diffusion-related, vulnerability-oriented, parameterizable time series, ES determinants. Outlier detection algorithms are intimately connected with robust statistics that down-weight some observations to zero especially in epidemiological, forecastoriented, signature, vulnerability models (e.g., Jacob et al. 2023). In future experiments we may define several outlier detection algorithms related to an empirical epidemiological dataset of georeferenced, hierarchical, diffusion-related, sub-county, hyper/ hypo-endemic, ES stratified, risk, model estimator determinants.
Next, we may apply asymptotic theory for evaluating the predictors. In statistics, asymptotic theory, or large sample theory, is a framework for assessing properties of estimators and statistical tests [15]. Within this framework, it is often assumed that the sample size n may grow indefinitely; the properties of estimators and tests are then evaluable under the limit of n → ∞. Subsequently, an ES modeler, researcher or data analyst may investigate the gauge (i.e., the fraction of wrongly detected disturbances) in the model and establish asymptotic normality and Poissonian theory for the gauge. Although contemporary oncological-related regression literature focuses on short-term forecast volatility modeling of georeferenceable, [GPS indexable], LULC stratifiable sub-county sampled determinants, [7] questions remains whether a Generalized Autoregressive Conditional Heteroscedastic (GARCH) model can reproduce similar attributes under multicollinear, asymptotical, zero autocorrelated, behavioral states using interpolated capture point signatures. A future ES researcher may consider the statistical inference of the class of asymmetric, power-transformed, eGARCH (1,1) models in presence of non-Gaussianism due to violation in regression assumptions when the strict stationarity condition is not met in an ES regression forecast vulnerability county model.
Doing so, would establish the non-asymptotic temporal normality of the quasi-maximum likelihood estimator when strict stationarity does not hold in an empirical georeferenced dataset of time series dependent aggregation/non-aggregation-oriented, ES (i.e., hot/cold spot) georeferenceable, estimator determinants sampled at the sub-county zip code level. Doing so, would also establish the optimal scalability of varying signature geospatiotemporal interpolatable LULC and sociodemographic, time series dependent ES capture points but without interception. An eGARCH (1,1) model with a skewed student’s t distribution should be tested for rectifying asymptoticalness, heteroscedasticity, latent multicollinearity and zero non-Gaussian autocorrelation in an empirical dataset of georeferenced time series sampled, ES stratified capture point determinants incorporating platykurtic and leptokurtic skewed thick tails. The results of the eGARCH (1, 1) may be validated using the post-ARCH test where the chi-square statistic may be decreased, hence revealing time homoscedastic ES determinants.
Subsequently, the capture point estimator determinants may be incorporated into a spatial Monte Carlo Markov Chain (MCMC), eigen-Bayesian, semi-parametric iterative non-frequentist model to rectify type I and type II errors due to violations of temporal regression assumptions. The model may verify if the ES regressed model forecasts comply with Tobler’s law of geography (i.e., non-chaotic, non-heteroscedastic, non-zero autocorrelated coefficients) [16]. The volatility clustering propensities rendered from the spatial, MCMC, eigen-Bayesian ES model may validate the determinant scalability incorporating eigen-orthogonal Moran’s eigenfunction eigenvectors. The test may exploit the existe of a universal estimator of a non-asymptotic time sensitive covariance matrix of the maximum likelihood estimator (MLE) for quantifying errors due to violations of regression assumptions in time space and geography in a prognosticative sub-county, ES estimator determinant model. By establishing the local nonasymptotic normality property in a nonstationary, signature, capture point, Markovian GARCH (1,1) model, an ES researcher may be able to tease out random non-Gaussian temporal patterns due to violations in regression assumptions in an empirical georeferenced, capture point, LULC and sociodemographic, estimator determinant dataset in time space and geography.
A social media platform using a real-time high-performance artificial intelligent (AI) interactive mobile iOS app may be then optimized for messaging and prioritizing prevention and treatment protocols to optimally regressively target and map vulnerable county-level ES stratified hot spots (i.e., aggregation of georeferenceable, non-zero autocorrelated, non-heteroscedastic, non-multicollinear, estimator determinants in a subcounty location). By adjusting for non-asymptotic normality due to violations of temporal regression assumptions in an AI infused smartphone dashboard, forecasts rendered from a signature county -level, capture point ES stratifiable, eigen-Bayesian semiparametric GARCH model would reveal, non-Gaussian real time detection of asymptotical heteroscedascity, latent multicollinearity and non-Gaussian zero autocorrelation coefficients in time series model. This data may aid in transforming ES stratified forecastoriented, vulnerability model independent variables so that they are compliant with Tobler’s law of geography, in so doing, social messaging primary prevention, timeliness early diagnosis and rehabilitation of ES patients at the county zip code level can be optimized in real time.
Conclusion
Given the volatility and shrouded nature of ES, this study was able to accurately, predictively model ES in a mostly unexplored fashion using advanced statistical models and georeferencing. The LULC autocorrelation map found that Thonotosassa was the hot spot for development of ES. A push for further clinical research on ES covariates linked to environmental factors and time (currently only utilizing race and age as definite predispositions), will allow us to utilize our current models used as well as time-based models to scale out our study to a larger scale to present with greater accuracy and reveal more opportunities for outreach and intervention.
References
- Durer S, Gasalberti DP, Shaikh H (2024) Ewing Sarcoma. StatPearls Publishing, Treasure Island, FL, USA.
- Hwang C, Agulnik M, Schulte B (2024) Prices and trends in FDA-approved medications for sarcomas. Cancers 16(8): 1545.
- McMahon KM, Nilles-Melchert T, Eaton V, Silberstein PT (2022) Effects of socioeconomic and geographic factors on outcomes in Ewing sarcoma: A National Cancer Database review. Cureus 14(5): e25525.
- McDowell S (2019) Cancer patients may not be told about costs of genomic testing. American Cancer Society, Atlanta, GA, USA.
- Dhir A, Rahul R, Liu Q, Pham D, Kronenfeld R, et al. (2024) Disparities in incidence and survival for patients with Ewing sarcoma in Florida. Cancer Medicine 13(8): e7151.
- Haight FA (1967) Handbook of the Poisson distribution. Wiley 18: 478-479.
- Satardekar A, Liu J, McDonald H, Jacob B (2024) Employing Markov Chain Monte Carlo (MCMC) Bayesian Poissonian and a second-order eigenfunction eigen decomposition algorithm to geostatistically target landscape covariates associated with leukemia in Hillsborough County, Florida. British Journal of Healthcare and Medical Research 11(4): 232-260.
- United States Census Bureau (2025) Explore Census Data. United States Census Bureau, Washington, DC, USA.
- Jacob BG, Izureta R, Bell J, Parikh J, Aceng JR, et al. (2023) Approximating non-asymptoticalness, skew heteroscedascity and geo-spatiotemporal multicollinearity in posterior probabilities in Bayesian eigenvector eigen-geospace for optimizing hierarchical diffusion-oriented COVID-19 random effect specifications geosampled in Uganda. American Journal of Mathematical Sciences 13(1):1-43.
- Griffith DA (2003) Spatial autocorrelation and spatial filtering: Gaining understanding through theory and scientific visualization. Springer, Berlin, Germany.
- Gelman A (2005) Analysis of variance? Why it is more important than ever. Ann Stat 33(1): 1-33.
- Cressie N (2015) Statistics for spatial data. John Wiley & Sons, Hoboken, NJ, USA.
- University of Rochester Medical Center (2025) Health encyclopedia. University of Rochester Medical Center, Rochester, NY, USA.
- Hosmer DW, Lemeshow S (2000) Applied logistic regression. Wiley, New York, USA.
- Estrada R, Kanwal RP (2012) A distributional approach to asymptotic. Springer Science & Business Media, New York, USA.
- Tobler WR (1970) A computer movie simulating urban growth in the Detroit region. Economic Geography 46: 234-240.
-
Clayton Moeller*, Namit Choudhari, Caleb Jaramillo, Aarya Satardekar, Nada Flaifl, Sasha Mosich,and Benjamin Jacob. Utilizing a Poissonian count variable Model, with a Second Order Eigen-Autocorrelation and a Hierarchical Bayesian Non-Frequentist Model to Forecast Hot-Spots of Potential Cases of Ewing Sarcoma in Hispanic Males in Hillsborough County, Florida, USA. Annal Biostat & Biomed Appli. 6(5): 2025. ABBA.MS.ID.000646.
Ewing sarcoma; hispanic; poisson; bayesian; hillsborough county; florida; iris publishers; iris publisher’s group
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






