Computer Aided Design of Robust Controller to Large Scale Power System

With the increasing dimensions and complexity of the interconnected power systems, LFC problem becomes one of the most important problems in electric power system stability. The decentralized control strategies are widely used recently because of the ability of using the traditional local control methodologies [1]. In the decentralized control, the large-scale power system is divided into many separated subsystem models and so the complex control problem can be decomposed into individual sub problems that have some interactions among each other. Currently the classical control techniques can be easily applied over subsystem level [2]. Each subsystem contains a local controller which can be of different type and has access to local sensors only [2].

Large-scale power systems usually consist of many control areas, connected by tie-lines to exchange the power demands among them [3]. Loads at any station can appear randomly and changeable so that the system frequency and tie line power will deviate from their nominal values. Decentralized control methods have been used during the last two decades to design LFCs with desired per formance to maintain frequency and tie line power flows at certain levels [4-7]. A change in real power demand at any point of a network is reflected throughout the system by a change in frequency. Therefore, system frequency provides a good indicator for system generation and load imbalance [8].

Linear quadratic optimal systems based on predetermined eigenvalues is an important manner. Alternative methods are developed to construct the weighting matrix Q that enable the user to shift undesired system eigenvalues (unstable or slow) ones into a pre-specified (stable or faster) ones [9-11]. The process can be repeated many times until all the desired pole locations are placed as required.

In order to solve the problem of complexity and large power system scales, many papers have applied modern optimization techniques to design robust controllers to LFC systems. Modern optimization algorithms are used to optimally adapt the conventional controller elements to LFC system. MVO is used with three-Degreeof- freedom for PID controller with imposed nonlinearities [12]. Improved MVO is applied to quickly optimize and find the Density- Based Spatial Clustering of Applications with Noise (DBSCAN) parameters corresponding to the highest clustering accuracy efficiently [13]. MVO and Salp Swarm Algorithm (SSA), are used for optimal tuning of Proportional-Integral-Derivative (PID) controller applied for LFC [14].

In this paper, MVO is applied to find the optimal feedback gains of LQR. The purpose of the methodology is to enable the system to beat specified uncertainties caused by variations of inertia constant (Mi) and tie-line synchronizing coefficient between area i and j, (Tij) parameters of all control areas and load disturbances. The first step is to divide the complex Multi Input Multi Output (MIMO) problem into simple Single Input Single Output (SISO) sub problems. LQR technique is used to design a local controller for each decoupled subsystem to realize design objectives. Moreover, slower eigenvalues are shifted more inside the stability region within prespecified values. In addition, MVO optimizer is applied to reach the optimal gains of LQR to enhance system stability. The proposed controller of MVO-LQR is evaluated and compared to the conventional LQR technique. This controller is fast to adapted because it is based on optimal gains calculated by LQR. The controlled system is composed again, and the overall stability is determined.

The conventional model is used for each control area of a multiarea power system which is widely used in many studies [9,10]. Referring to the simplified traditional-based LFC model shown in Figure 1 for control area1, the state space realization of area i (from 4-control arsea power system) is given by (1):

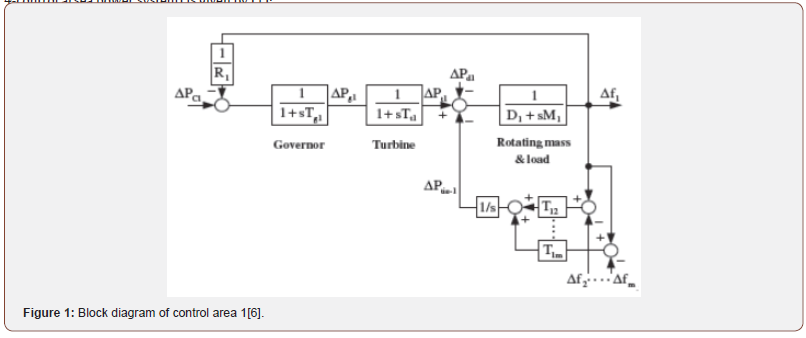
The state vector x_i control input u_i, disturbance input w_i and the measured output y_i can be defined as

where:
Δf_i : frequency deviation of area i
ΔP_gi : governor valve position of generator in area i
ΔP_ci : governor load set point in area i
ΔP_ti : turbine power in area i
ΔP_tie-i : change in net tie-line power flow in area i
ΔP_di : disturbance in area i
M_i : equivalent inertia constant for area i
D_i : equivalent damping coefficient for area i
g_i : governor time constant for area i
T_ti : turbine time constant for area i
T_ij : tie-line synchronizing coefficient between area i and j
R_i : drooping characteristic for area i

In which m A ϵ R^16x16, B ϵ R^16x4, W ϵ R^16x4, and C ϵ R^4x16 as represented in [6].

The total real power imported to area i equals the sum of all inflowing line powers ΔP_tie-ij from adjoining areas as

The real power in per unit transmitted across a lossless line of reactance X_ij is

where:
P_ri : is the rated power of area i,
V_i and ϴ_i : are the amplitude and angle of the terminal voltage in area i.

LQR is an optimal design technique guarantee robustness. Hence the procedure in designing a linear quadratic system with prescribed poles developed by Solheim O.A. [9] to shift slow decoupled subsystem’s eigenvalues. This method confronts the effect of interaction between the interconnected sub systems that leads to a much more stable overall system poles and enhance the overall system stability.

The optimal gain is determined to minimize the cost function J

Where matrices R and Q are the weighting matrices of the input and states, respectively and k is given by

where P is the unique, symmetric, positive definite solution to steady state Algebraic Ricatti Equation (ARE)

Equation (10) is used to construct the weighting matrix Q to shift complex conjugate poles to desired complex places with the constraint in (11), to compute its internal elements

And (12) can be used to shift complex conjugate to real places with the constraint in (13)

whereas if it is required to shift the real eigenvalues to new real places use (14)

Where the old locations S_j=-α+jβ, and the desired locations S_p=- σ+jω are for complex and λ_i for real.

In this algorithm, a population based dividing the problem into two phases: exploration and exploitation. White hole and black hole concepts are used as exploration and wormhole is treated as exploitation in this algorithm. The rules have been applied in MVO to the universe are [15]:

Higher inflation rate leads to a higher probability of having white hole and also, a lower probability of having black holes. In this case, universes tend to send objects through white holes whereas in lower inflation rate it tend to receive more objects through black holes. Regardless of the inflation rate, the objects in all universes may move randomly towards the best universe via wormholes. The conceptual of this algorithm is depicted in (Figure 2).

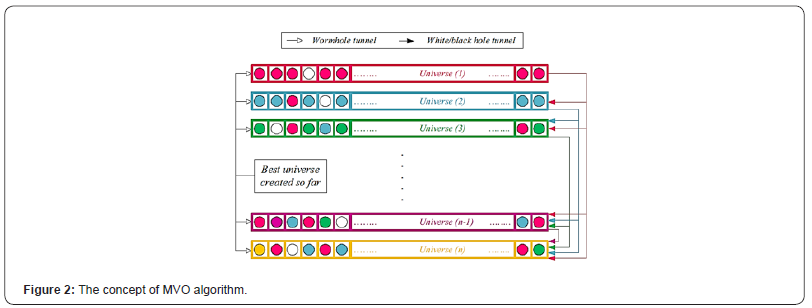
The development of MVO initially can be described as the following expression

where U is a set of x_ij solution, d is the number of variables (dimension) and n is the number of universes (candidate of solution) which can be described as follows:

where x_i^j is the jth parameter of i^th universe, U_i shows the universe, NI(U_i) is normalized inflation rate of the i^th universe, r1 is a random number between 0 and 1, and x_k^j is the j^th parameter of k^th universe selected by a roulette wheel selection mechanism.

The universes keep exchanging objects without perturbation. To maintain the diversity of universes and to exploit the searching process in MVO, each universe is treated to have wormholes to transport its objects through space randomly. For high probability of improving the inflation rate and make local changes for each universe using wormholes, always, that wormhole tunnels are established between a universe and the best universe formed so far, and can be described as follows:

TDR (travelling distance rate) and WEP (wormhole existence probability) are coefficients, lb_j and ub_j are the lower bound and upper bound of j^th variable respectively and r₂, r₃, and r₄ are random numbers between 0 and 1. WEP and TDR are treated as adaptive formula as follow:

where min is the minimum of optimization problem variables, max is the maximum, l is the current iteration, L is the maximum iterations and p is the exploitation accuracy over the iterations. The higher p, the sooner and more accurate exploitation/ local search. MVO algorithm depends on number of iterations, number if universes, roulette wheel mechanism and universe sorting mechanism. Quick sort algorithm is used to sort universe at each iteration and roulette wheel selection is run for every variable in every universe over iterations.

Matlab software has been used to design and evaluate the effectiveness of the proposed methodology. System simulation parameters are considered as in Appendix Table 1 & 2 These values make the system stable, whereas the performance is affected by change in the equivalent inertia constants M_i and synchronizing coefficients T_ij more than changes of other parameters, these parameter values may lead the system into the instability region Table 3. The maximum value of dead band for governor is specified as 0.05 p.u and generation rate constraint (GRC) of 10% per minute and for each area are considered in the simulation [2]. Where the value of (P_e)_Base is 800MVA.

Table 1:Controlled System Specifications Using MVO-LQR.

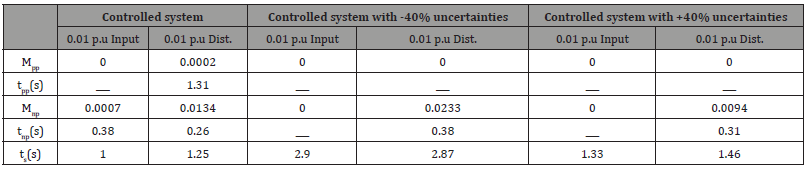
where: M_pp is the maximum positive peak (Hz) and M_np is the maximum negative peak (Hz), Dist. means disturbance in per unit (p.u), and t_s is the settling time in (Sec).

Table 2: Nominal Power System Parameter Values.

Table 3:Parameter Variation Limits Lead to System Instability.

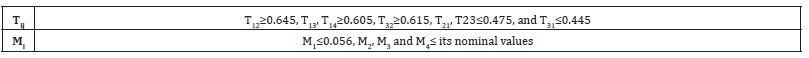
The system is decomposed into four decoupled subsystems by the method that well explained by [16]. LQR method is used as a conventional method of design, all the internal elements of the weighting matrices Q are calculated as discussed in section III for each subsystem to shift the undesired subsystem eigenvalues into much stable places.
Q₁ = diag ([1 50763.88 118.6256 118.6256])
Q₂ = diag ([1 1773.63 11.14611 11.146])
Q₃ = diag ([1 133906.1 76.385 76.385])
Q₄ = diag ([1 8.337*10^6 51.966 51.966])

MVO algorithm is used as the procedures in Figure 3. To determine local controller gains K₁, K₂, K₃, and K₄ for the controlled system to minimize system objective function

With the constraints of accepted maximum overshoot (0.05) and a settling time of 4 sec, the parameters of the optimizer are adapted according to the design requirements to: WEP_min= 0.2, WEP_max= 1 and p= 6

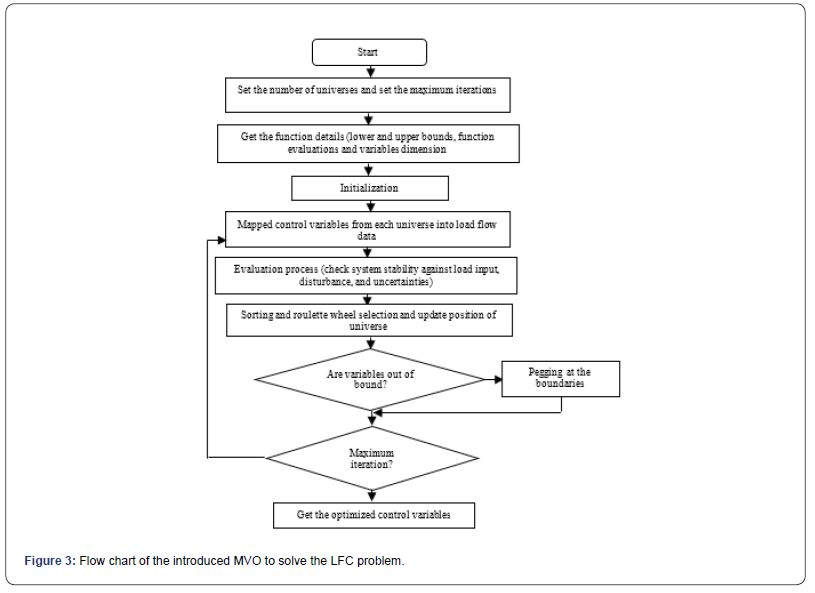
The optimization was repeated 30 times and the best solution is considered as proposed local controller parameters.
K₁= [676 -36 676 676]
K₂= [991.3 570.66 991.3 991.3]
K₃= [860 -294.6 860 860]
K₄= [1000 10120 1000 1000]

Also, global controllers are determined, K₁₂, K₁₃, K₁₄, K₂₁, K₂₃, K₂₄, K₃₁, K₃₂, K₃₄, K₄₁, K₄₂, and K₄₃. And the overall controller gain is calculated as in [16].

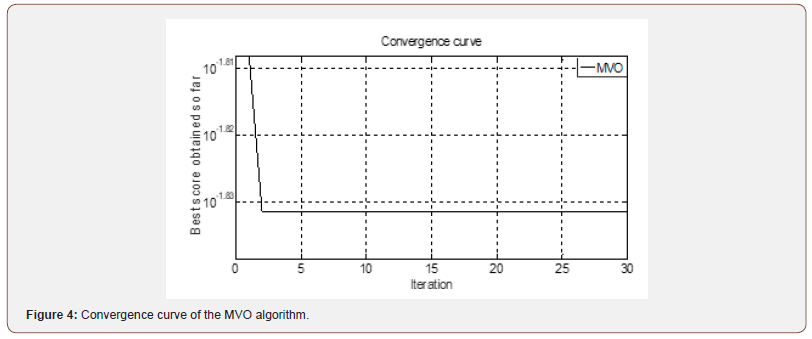
The objective function via iterations has been shown in Figure 4. From which figure the MVO algorithm has been reached the optimal adjusting of the LQR in iteration 4.

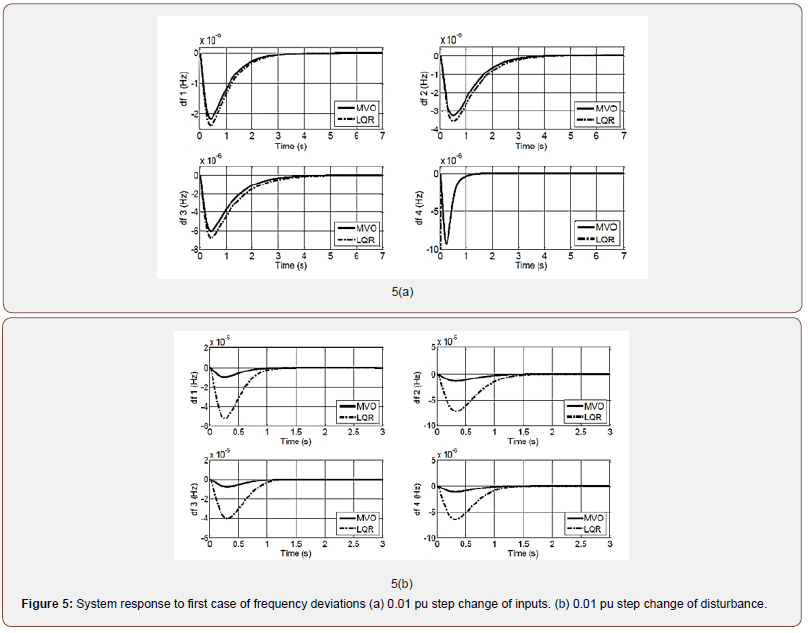
• Case 1: System performance of the proposed MVO-LQR controller and the conventional LQR are tested for nominal parameters to step input and load-change. Figure 5 (a) and (b) illustrate the simulation results of the frequency deviation for each area for 0.01 p.u. input and 0.01 p.u disturbance load respectively. It is obtained that system with MVO-LQR controller is more stable and fast as compared to the controlled system with traditional LQR (Figure 5a, 5b).

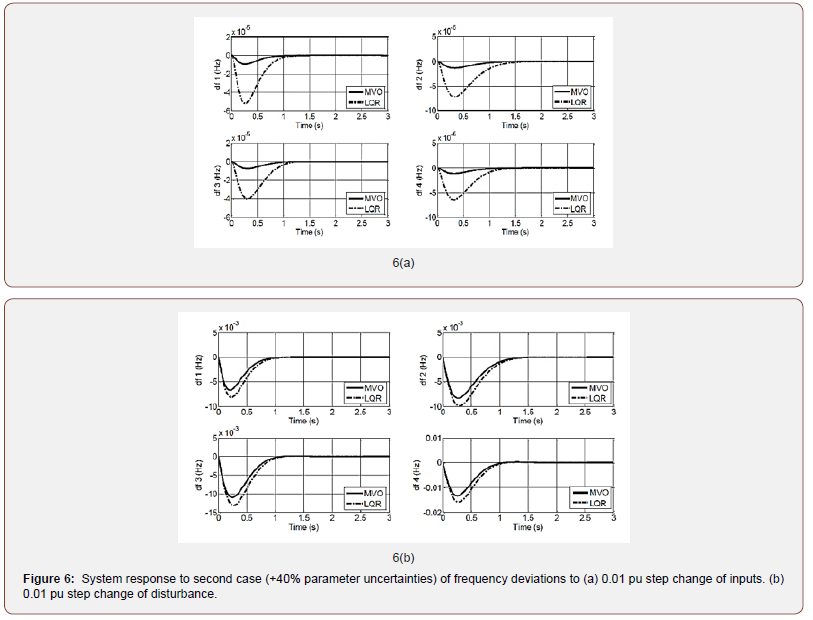
• Case 2: The robustness of the proposed MVO-LQR controller in face of a wide range of parameters uncertainty is validated. System parameters M_i and T_ij have been changed to +40%. Figure 6 depicts the response of the four areas in the presence of above uncertainty. A desirable and faster performance response has been achieved using the proposed MVO-LQR comparing to the presented LQR technique.

• Case 3: The controlled system is validated facing parameters change of -40%. Figure 7 depicts the response of the controlled system in the presence of above uncertainty. A relatively desirable performance response has been achieved using the proposed MVO-LQR over LQR only.

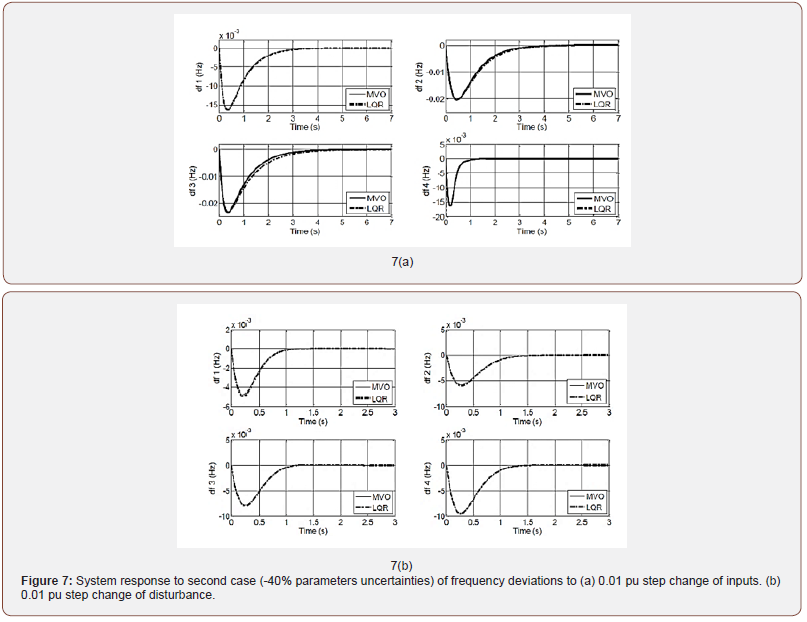
The controlled system specifications using MVO-LQR has been calculated for all different cases and summarized in Table 1. It has shown that the resulted specifications of the proposed MVO-LQR are acceptable (Figure 6a,6b 7a,7b) (Table 1).

A robust decentralized controller is designed by the aid of modern MVO algorithm to control a four-area interconnected power system. Local controllers are designed using LQR to relocate system’s unstable/slow eigenvalues into prespecified stable/faster ones. MVO is generated to find the optimal and local controller gains based on that calculated by LQR. Global controllers are calculated to reduce the effect of the interconnected subsystems among each other. Simulation results demonstrate that the power system with MVO-LQR controller is robust in face of load change and parameter perturbation within ±40% uncertainties. The dependency of MVOLQR on the pre calculated gains results in shorter run time and smaller number of iterations. The resulted controlled system has desirable performance and smooth response compared to that resulted by the conventional LQR controller.

None.

None.

1. Zheng Y, Zhou J, Xu Y, Zhang Y, Qian Z (2017) A distributed model predictive control based load frequency control scheme for multi-area interconnected power system using discrete-time Laguerre functions. ISA Transactions 68: 127-140.
2. Pandey SK, Mohanty SR, Kishor N (2013) A literature survey on load–frequency control for conventional and distribution generation power systems. Renewable and Sustainable Energy Reviews 25: 318-334.
3. Dao T, Wangl Y, Nguyen N (2016) Novel Hybrid load-frequency controller applying artificial intelligence techniques integrated with superconducting magnetic energy storage devices for an interconnected electric power grid. Arab J Sci Eng 41: 3309-3332.
4. Selvakumarana S, Parthasarathy S, Karthigaivel R, Rajasekaran V (2012) Optimal decentralized load frequency control in a parallel AC-DC interconnected power system through HVDC link using PSO algorithm. Energy Procedia 14: 1849-1854.
5. Shayeghi H (2008) A robust decentralized power system load frequency control. Journal of Electrical Engineering 59(6): 281-293.
6. Bevrani H, Mitani Y, Tsuji K (2004) Sequential design of decentralized load frequency controllers using µ synthesis and analysis. Energy Conversion and Management 45: 865-881.
7. Bernard MZ, Mohamed TH, Qudaih YS, Mitani Y (2014) Decentralized load frequency control in an interconnected power system using coefficient diagram method. International Journal of Electrical Power & Energy Systems 63: 165-172.
8. Elsisi M, Soliman M, Aboelela MAS, Mansour W (2017) Optimal design of model predictive control with superconducting magnetic energy storage for load frequency control of nonlinear hydrothermal power system using bat inspired algorithm. Journal of Energy Storage 12: 311-318.
9. Solheim OA (1972) Design of optimal control systems with prescribed eigenvalues. Int J Control 15(1): 143-160.
10. Ghoreishi SA, Nekoui MA, Basiri SO (2011) Optimal design of LQR weighting matrices based on intelligent optimization methods. International Journal of Intelligent Information Processing 2(1).
11. Stefanescu RM, Prioroc CL, Stoica AM (2013) Weighting matrices determination using pole placement for tracking maneuvers. UPB Sci Bull Series D 75(2): 31-40.
12. Mudi J, Shiva CK, Mukherjee V (2019) Multi-verse Optimization Algorithm for LFC of Power System with Imposed Nonlinearities Using Three-Degree-of-Freedom PID Controller. Transactions of Electrical Engineering, Elsevier 43(4): 837-856.
13. Lai W, Zhou M, Hu F, Bian K, Song Q (2019) A New DBSCAN Parameters Determination Method Based on Improved MVO. IEEE Access pp. 104085-104095.
14. Gunjan D, Sathans S (2020) A comparative study of MVO and SSA optimized PID controller for LFC in EV integrated multi area network. 11^th International Conference on Computing, Communication and Networking Technologies (ICCCNT) Computing pp. 1-7.
15. Mirjalili, Mirjalili SM, Hatamlou A (2016) Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Computing & Applications 27(2): 495-513.
16. Siljak D, Vukčevic M (1976) Decentralization, stabilization, and estimation of large-scale linear systems. IEEE Transactions on Automatic Control 21(3): 363-366.