Dynamic Time Warping for Time Series Curve Similarity

The judgement and evaluation of the similarity between time series curves have extensive research needs and application values. These tasks enable functions such as prediction, decision making, pattern recognition and understanding, abnormal detection, and diagnosis and are the foundation and key technology in many fields. For example, comparing traffic flow changes during traffic analysis with changes in environmental parameters or other time series can help determine road conditions and traffic management planning. In speech and image processing, comparison of the similarity of speech data, image data, and other time series or spatial dimensions can be used for classification, clustering, and filtering. For medical diagnosis, comparing changes in patients’ physiological indicator curves over time can aid in determining disease progression and prognosis. The evaluation of time-series curve similarity requires extensive research and application. It realizes functions such as prediction, decision-making, pattern recognition and understanding, abnormal detection, and diagnosis. This is the foundation and key technology in several fields.

However, the time-series curve similarity analysis presents several challenges. These include noise and irregularities in timeseries data. Real-world time-series data frequently contain noise, missing values, and irregularities, which make similarity analysis challenging. Therefore, preprocessing and smoothing techniques are required. In addition, owing to time shifting and scaling, time series curves can be shifted in time or scaled in amplitude, thereby impacting similarity computations. Aligning and normalizing the time series is often necessary. The Frechet Distance algorithm measures the similarity between curves. It defines the distance between two curves, which can be regarded as how one curve must deform to completely coincide with the other. However, its computational complexity is high, and it is sensitive to noise and time shifts. Dynamic time warping (DTW) and deep learning are two major approaches to time-series curve similarity. DTW is simple, fast, and interpretable but limited in its ability to handle complexity or discover similarity metrics on its own. Deep learning can discover complex similarity relationships and metrics but requires more data and resources. It lacks interpretability. The choice among these methods depends on factors such as data properties, problem complexity, and available resources. Compared to other algorithms, the DTW method is a fast and simple method that is easy to implement with relatively lower computational resources. This paper presents an interesting application of improved DTW for time-series curve similarity. An experiment based on real data (financial market data) was conducted. The raw data were preprocessed using min-max normalization, and the algorithms of the Frechet Distance and DTW were compared.

The Frechet Distance algorithm measures the similarity between curves. Buchin, K. et al, 2013[1] developed the Frechet distance to compare multiple curves using the concept of the Fréchet distance between a single curve and a set of curves. Maheshwari and Yi 2018 [2] provided a comprehensive survey of algorithms and approximation techniques for computing the discrete Frechet distances between curves.

The main idea of the Frechet Distance algorithm is to treat the two curves as two polylines connected by discrete points and try to find a path such that the maximum distance on this path is minimized.

The Frechet Distance algorithm steps are as follows:
1. Determine the set of points on the two curves, denoted as P = {p1, p2, ..., p_n} and Q = {q1, q2, ..., q_m}.
2. Initialize matrix F as a full matrix, where F (i,j) represents the maximum distance between the first i points of P and the first j points of Q.
3. For the last point pn of P and qm of Q, let F (n, m) = d (p_n, q_m) 4. Backtrack the path, there are two cases for F (i,j):
a) If there is a connection path between p_i and q_j, then F (i,j) = max (F (i-1, j), F (i, j-1), d (p_i, q_j))
b) If there is no connection between p_i and q_j, then F (i,j) = max (F (i-1,j), F (i,j-1))

The advantage of the Frechet Distance algorithm is that it considers the topological relationship between each point on the curve; thus, it can accurately measure the similarity of curves. However, its computational complexity is high, and it is sensitive to noise and time shifts. Dynamic time warping (DTW) is an improved algorithm for calculating the similarity between two time series. Keogh and Pazzani (2001) [3] introduced an improvement in dynamic time warping (DTW) for time-series similarity specifically designed for datasets with high noise levels. Wang et al. (2013) [4] provided an empirical comparison of many time-series representation methods and distance measures (e.g., Euclidean and DTW) on 85 datasets. It finds no single best method and depends on the data properties. Wang et al. (2018) [5] provided an overview of time series similarity learning, including representation learning, kernel learning, and other techniques developed since 2015. proposed a generic framework to integrate different methods. Franses and Wiemann applied intertemporal similarity to economic time-series data [6]. Abdelmadjid and Bachir (2021) presented a similarity measure for long time-series classification based on local extrema and dynamic time warping [7], and Agnieszka et al. (2022) evaluated time-series similarity using concept-based models [8]. DTW is a classic algorithm that calculates the optimal alignment between two time series by warping them non-linearly. It has been used for decades and remains a strong baseline. It can handle time shifting and non-linear relationships but has difficulty with high dimensionality, noise, and complex relationships. It uses a simple distance measure to compare the aligned time series. They cannot discover complex similarity metrics or representations on their own.

Fawaz et al. (2019) [9] reviewed recent deep learning methods applied to time series classification, including CNN, RNN, LSTM, and convolutional kernel learning techniques. Several methods can be adapted for similarity learning. Qahtan et al. (2020) [10] reviewed CNN, RNN, LSTM, and other deep neural network methods applied to time-series classification since 2015. Most techniques can be adapted for similarity learning and comparison. Unlike DTW, deep learning uses neural networks to automatically learn hierarchical features, metrics, and other complex relationships within timeseries data. It can handle high dimensionality, noise, and complex time-series relationships without requiring as much parameter tuning or domain expertise as possible. Deep learning identifies complex non-linear similarity metrics and data representations that can change over time. The features and comparisons made are learned from the data, not predefined. However, deep-learning models require large amounts of training data and computing resources. They can be slow to train and are often seen as “black boxes” that lack interpretability.

The DTW method is a fast and simple method that is easy to perform with relatively low computational resources. The basic idea of the DTW algorithm is to project one time series onto another time series of the same length such that the Euclidean distance between the two sequences is minimized. The main steps of the algorithm are as follows.
1. Calculate the distance (Euclidean distance, Manhattan distance, etc.) between the corresponding positions in the two sequences.
2. Construct a distance matrix, where each element represents the minimum distance from a position in the first sequence to a position in the second sequence.
3. Starting from the upper left corner of the distance matrix, calculate the distance of each position in turn and find the minimum path (i.e., minimum distance) to reach that position.
4. According to the minimum path, a path from the starting point of the first sequence to the end point and then to the end point of the second sequence can be found. This path is the warping path, and the nodes on the warping path represent parts with similarities between the two sequences.
5. The similarity measure between two sequences can be calculated according to the nodes on the warping path.

Typically, the average value of the corresponding elements on the warping path in the distance matrix is used to represent this.

The advantages of the DTW algorithm are that it can handle sequences of unequal length and does not require time points to be aligned.

As shown in Figure 1, the abscissa represents nine points in segment A and the ordinate represents seven points in segment B, forming a 7 × 9 matrix. In matrix (denoted as W), the blackened part indicates the Euclidean distance between the points in segment A and the shortest points in segment B. When the DTW algorithm warps the two segments in the matrix, it satisfies the following three constraint conditions.

Boundary condition: The order cannot change; the selected path must start from the upper-left corner and end at the lower-right corner.
Continuity: For the next point, Wk= (a, b) on the path, it is impossible to skip a point to match and can only align with its adjacent points.
Monotonicity: The forwarding points must proceed monotonically with time.

Finally, the distance between the matched points on this path is added to obtain the similarity value between the two curves. The smaller the value, the more similar the two curves. Commodity price trends in the financial market often exhibit typical patterns, such as W-shape and M-shape. These patterns contain two large fluctuations, and the position of the intermediate inflection point, and the direction of the subsequent trend change can be used to determine market sentiment and trend changes. The appearance of a W-shape indicates that the commodity price trend has changed from declining to rising. After the W-shaped pattern is confirmed, investors can buy stocks to profit. However, the appearance of an M-shape usually indicates that the stock price trend has changed from rising to declining. After the M-shaped pattern is confirmed, investors can sell stocks to profit or avoid losses. In this study, the benchmark time-series curves for similarity matching were specified as typical W-type- and M-type curves. The real commodity price trends were recorded as testing curves to match the W-shape and M-shape using algorithms such as Frechet Distance and DTW.

Real data from the domestic financial market, including 20 different stocks, were used to perform similarity calculations for the last year (from 2022-07-01 to 2023-05-31). Each record of commodity data has attributes such as trade date and closing price. For example, the first batch of test data was 000002. SZ (the stock price of the Wanke Company), with the close prices shown in Figure 1.

The W-shaped curve and its feature parameters are shown in Figure 2. The key features of this pattern include five data points with X (time) values of [0, 5, 10, 15, 20] and Y values of [20, 15, 19, 13, 18].

The M-shaped curve and its feature parameters are shown in Figure 4. The key features of this pattern included five data points, with X (time) values of [0, 5, 10, 15, 20] and Y values of [80, 100, 80, 110, 80].

The point-slope equation was used to obtain the front and back coordinates of the line segments, which were connected one by one to obtain the M-shape formula, as shown in Equation (6-1), where i=0,1,2,3,4.

Then, according to the horizontal coordinate X of each point, and then every interval between the two horizontal coordinates to obtain an X coordinate corresponding to the Y-axis coordinates, that is, the last Y-axis coordinates to generate the typical form of Wor M-shaped data sequence, with a number of curve dots (denoted as NumDot). Referring to Figure 3 and 4, there are five dots that represent the curve, and the NumDot is 5. If we redefine and let NumDot be 300, 300 dots are used to represent the image of the curves. Therefore, the data sequence of the M-shape is as follows (refer to Figure 5):
NumDot =300
X = [0,1,...,298,299]
Y = [80.4,80.8,...,81.2,80.6,80]

Because the Y-axes of the three curves are not at the same height, they need to be normalized to converge to a similar range. This is done using the min-max normalization function, which normalizes the Y-axis data of the three arrays to the 0-1 interval in equal proportions, as shown in Equation (6-2).

where y’ and y’ specify the raw commodity price and afterprocessed prices, respectively.

The red dashed line in Figure 6 represents the data sequence of the M-shape, the blue dashed line represents the data sequence of the W-shape, and the green dashed line shows the trend of the test sample data. The Frechet Distance and DTW algorithms were used to calculate the final matching result of the test sample curve. In the following experiment, the DTW and Frechet algorithms were used to compare the morphology of the sample with the characteristic samples of the collected time series data to obtain their similarity values with M-shape (denoted as M) and W-shape (denoted as W). The measurement of the difference (%) was defined as follows:

The difference (%) between the similarity values of the W-shape and M-shape is calculated to determine the clarity of the algorithm’s matching result. The pattern curve matched by the algorithm is then determined by selecting the one with the smallest similarity value between the W-shape and M-shape.

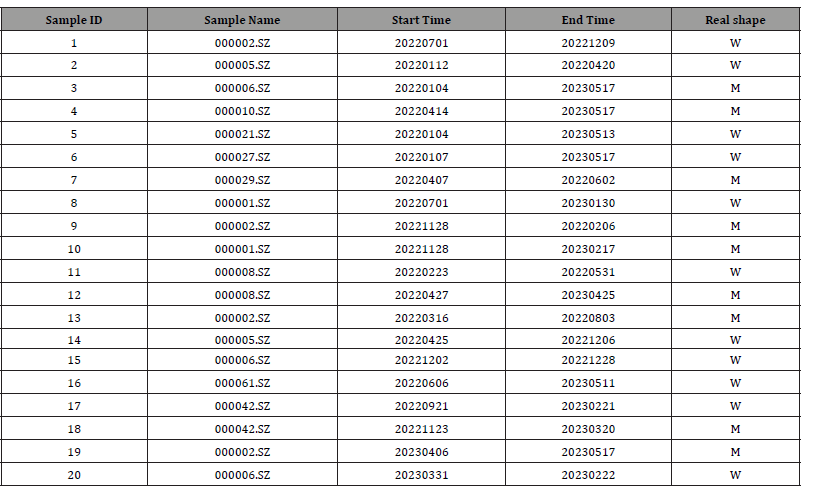
In this experiment, 20 groups of test data were examined. The sample data are presented in Table I. The first and second columns indicate the ID and names of data sample groups, respectively. The fourth and fifth columns indicate the start and end times of the time series data segment, respectively. The last column presents the true patterns and shapes of the samples.

Table 1:The sample Data.

Twenty groups of data were tested with the NumDot set to 250. Table II shows the calculation of the similarity values using the DTW and Frechet algorithms. A smaller distance indicates higher similarity to a typical shape (W or M shape). The last two columns provide judgement results (1 for yes and 0 for no), with the values inside parentheses representing the difference values (%), as defined in equation (6-3).

Table 2:Calculation And Judgement (Numdot= 250).

For example, as shown in Table II, sample ID 1 (from July 1, 2022, to December 9, 2022, also referring to Table I) has a true W-shaped pattern. When calculated using the DTW algorithm, the similarity values for the W-shape and M-shape were 1.915 and 2.927, respectively, and the difference between the two similarities was 52.85%. This indicates that the matching pattern of this curve fragment was W-shaped.

Comparing the two algorithms, it appears that the DTW algorithm is superior in the process of curve similarity comparison. The average accuracies of the DTW and Frechet algorithms are 90% and 65%, respectively. The average difference value (%) of the DTW algorithm’s comparison results was 57%, whereas that of the Frechet distance algorithm was only 0.01%. This indicates that the difference between the similarity values of the DTW algorithm’s comparison results is more obvious and helpful in judging the matching results. As the value of NumDot increases from 250 to 500, 750, 1000, 1250, 1500, 1750, and 2000, the results are summarized in Figures 7 and 8. Considering the different values of NumDot, Figure 7 shows that the total average accuracies for the DTW and Frechet algorithms are 91.88% and 54.38%, respectively, for different sample data. As shown in Figure 8, as the value of NumDot increases, the accuracy of the DTW and Frechet algorithms is not significantly affected. For the Frechet algorithm, the best result was obtained when NumDot was set as 250. As the value of NumDot increased, the accuracy of the DTW algorithm improved slightly.

This paper presents the verification and comparison of the DTW and Frechet algorithms for time-series curve similarity. Through experimentation, it was found that both the DTW and Frechet algorithms do not require time-series curves to be aligned on the time axis and can handle time-series curves of different lengths. The DTW algorithm can tolerate anomalies and distortions on the time axis of time-series curves, and by finding better and optimal non-linear matching, it can obtain more accurate results than the Frechet algorithm.

A comparison of the two algorithms indicates that the difference between the similarity values of the DTW algorithm’s matching is more obvious and helpful in judging the matching results. Further research is required to consider more scenarios, such as larger datasets or more complicated curve shapes. Future research will be conducted to determine whether improved versions of the DTW algorithm are suitable for fast matching in big data environments or ultra-large datasets.

None.

No conflict of interest.

1. Buchin K, Buchin M, and Schulz A (2013) On the Frechet distance of a set of curves. Computational Geometry 46: 1016-1026.
2. Maheshwari A, Yi J (2018) A Survey of Techniques for Efficiently Computing Fréchet Distance. Computational Geometry and Graph Theory, Springer.
3. Eamonn Keogh, M Pazzani (2001) Derivative Dynamic Time Warping. In First SIAM International Conference on Data Mining (SDM'2001).
4. Wang X, Mueen A, Ding H, Trajcevski, G., Scheuermann, et al. (2013) Experimental comparison of representation methods and distance measures for time series data. Data Mining and Knowledge Discovery 26(2): 275-309.
5. Wang J, Zhao P, Cui S, Liu M (2018) Time series similarity learning: From raw data to representation and kernel learning. Neurocomputing 275: 2285-2302.
6. Franses PH, Wiemann T (2020) Intertemporal Similarity of Economic Time Series: An Application of Dynamic Time Warping. Comput Econ 56: 59-75.
7. Abdelmadjid Lahreche, Bachir Boucheham (2021) A fast and accurate similarity measure for long time series classification based on local extrema and dynamic time warping, Expert Systems with Applications 168: 114374.
8. Agnieszka Jastrzebska, Gonzalo Nápoles, Yamisleydi Salgueiro, Koen Vanhoof (2022) Evaluating time series similarity using concept-based models, Knowledge-Based Systems 238: 107811.
9. Ismail Fawaz H, Forestier G, Weber J, Idoumghar L, Muller PA (2019) Deep learning for time series classification: a review. Data Mining and Knowledge Discovery 33(4): 917-963.
10. Qahtan AA, Alharbi S, Wang S, Zhang X (2020) Deep learning in time series classification: A review. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 10(1): e1319.