The Anthropological Dimension on Ethnomodelling Research Based on Ethnomathematics and Modelling

When researchers investigate the knowledge and traditions possessed by members of diverse cultural groups, they may be able to find distinctive mathematical ideas and/or characteristics that can be labelled ethnomathematics. As well, an outsider’s understanding of cultural traits is in danger of misinterpretation or bias that may over emphasize inessential features and create misinterpretations of this mathematical knowledge. The challenge arising from this approach is related to how we can find and understand culturally bound mathematical ideas without letting the culture and academic background of the researcher or investigator interfere with the culture of the members of the cultural group under study, and this happens when members of distinct cultural groups share their own interpretation of their culture (emic) opposed to an outsider’s interpretation (etic).

Researchers and educators who take on an emic perspective believe that factors such as cultural and linguistic backgrounds, social and moral values, and lifestyle come into play when mathematical ideas, procedures, and practices are developed by the members of cultural groups. Yet, their interpretation is at risk because of either known or unknown biases. The ideas that members of distinct cultural groups have developed different ways of doing mathematics in order to understand and comprehend their own cultural, social, political, economic, and natural environments [1] is often controversial with in the mathematics community. Researchers in ethnomathematics affirm, however, that many cultural groups have developed their own unique and distinct ways to mathematize their own realities and environments [2,3]. Mathematization is the process by which members of distinct cultural groups think mathematically and interpret their environment through the use of mathematics, most notably, through counting, measuring, patterning, gaming, quantifying, etc. Often, these members have developed successful and distinct mathematical tools that allow them to organize, analyse, comprehend, understand, and solve specific problems located in the context of their real-life situation [4]. These tools allow for identification and description of specific mathematical ideas and/or practices by schematizing, formulating, and visualizing a problem in different ways, discovering relations, discovering regularities, and translating real-world problems through mathematization.

It is important to search for alternative methodological approaches in relation to the development of mathematical practices. Through various forms of colonization and global capitalism, worldwide and for better or worse western academic mathematics is accepted as the universal standard in order to record forms of mathematics that developed over time in diverse cultural contexts. One alternative methodological approach to this approach is ethnomodelling, which we consider as the practical application of ethnomathematics, and which adds a voice of members of distinct groups as well cultural perspectives to the mathematical modelling process that seeks for the decolonization of the educational process through changes in the content and delivery of the mathematics curriculum as well to examine power relations within society. In this context, decolonization is defined as and can be considered the “centering our [local] concerns and worldviews and then coming to know and understand theory and research from our [local] own perspectives and for our own purposes” [5]. Similarly, Battiste et al. [6] defined decolonization of education as the examination of the assumptions inherent in western knowledge, science and modern educational theory in order to make visible and dispel the assumption that local “knowledge is primitive and in binary opposition to scientific, western Eurocentric or modern knowledge”. In addition, the objective of decolonizing education is the local resurgence and empowerment [6].

For example, Eglash stated that the epistemological basis of ethnomathematics is not restricted to methods of direct and/or literal translations used in non-western mathematical practices to the western traditions. This investigator considers that this consists of historical studies that emphasize cultural procedures and practices [7], which developed by ancient civilizations such as found in Chinese, Hindu, and Muslim contexts. For example, the “Chinese Chu Shih-Chieh triangle can be mapped onto Pascal’s triangle by a rotation of ninety degrees” [8]. In this context, Eglash [9] also states that ethnomathematics includes mathematical patterns developed in the modelling approach that strives to include conscious intent as an important component for the analysis of mathematical anthropology that uses modelling in ethnographic and archaeological studies to describe material and cognitive structures without attributing conscious intent to members of distinct cultural groups. These patterns are instead seen as the structural basis of underlying social forces or as epiphenomena resulting unintentionally from the nature of the activity itself. For example, the refinements of mathematical anthropology expanded initial analysis to a variety of social phenomena and increasingly complex mathematical tools [9,10]. In our work, we emphasize justifying the need for a culturally bound approach on mathematical modelling with sources rooted on the theoretical basis of ethnomathematics. In this regard, Barton [11] affirms that, in the ethnomathematics program, mathematical practices are culturally specific because it implies in some form of relativism for mathematics.

Studies conducted by anthropologists and investigators, such as Ascher [12], Closs [13], Orey [14], Rosa & Orey [15] and Urton [16], “have revealed sophisticated mathematical ideas and practices that include geometric principles in craft work, architectural concepts, and practices in the activities and artefacts of many indigenous, local, and vernacular cultures” [17]. These concepts are related to diverse numeric relations found in measuring, calculation, games, divination, navigation, astronomy, modelling, and a wide variety of other mathematical ideas, procedures, and cultural artefacts [17]. Thus, a “body of anthropological research has come to focus on both intuitive mathematical thinking and the cognitive processes largely developed in minority cultural groups” [1]. In this approach, it is necessary that educators:

(...) possess knowledge of the cultural traditions, linguistic backgrounds, and mathematical ideas, procedures, and practices students develop in the classrooms. Thus, teachers must develop an anthropological perspective in relation to the learning process in order to help them to deal with the school environment as well to the diverse culture’s students bring to the school. Thus, it important to propose the use of anthropological studies to the development of the learning process in general [12]. Ethnomodelling may be considered as the intersection area between cultural anthropology, ethnomathematics, and mathematical modelling (Figure 1), and which is used to help members of distinct cultural groups to translate diverse mathematical ideas practices and practices found in their own communities [18] (Figure 1).

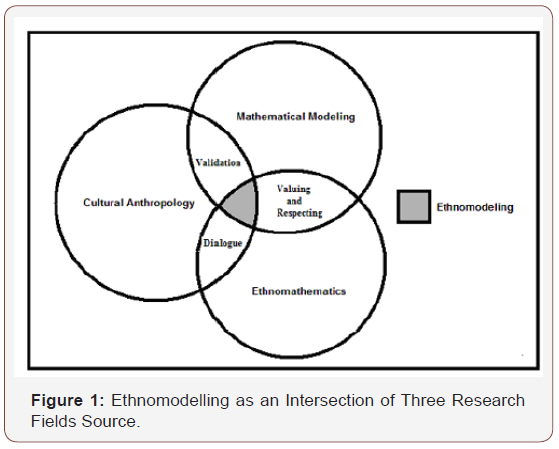
For example, Figure 1 shows that during the development of the ethnomodelling process, the “intersection between mathematical modelling and ethnomathematics relates to the respect and the valorization of the previous knowledge and traditions developed by students, which enables them to assess and translate problemsituations by elaborating mathematical models in different contexts”.

Consequently, it is recommended that educators:

(...) start by using sociocultural contexts, realities, and the many interests and needs of students and not mere enforcement of a rigid set of external values or often-decontextualized curricular activities. This approach facilitates the development of dialogue between mathematical modelling and cultural anthropology in order to reach a critical transitivity, which is a horizontal rather than a vertical or hierarchical relationship.

The diagram depicted in figure 1 also shows that:

(...) local knowledge becomes the intersection between ethnomathematics and cultural anthropology when members of distinct cultural groups use it to solve problems faced in their own contexts. It also becomes a body of knowledge often built up by these members over time and across generations of living in close contact with their own historical, social, cultural, and natural environment [1]. In this context, Eglash et al. [17] stated that “cultural anthropology has always depended on acts of ‘translation’ between emic and etic perspectives”. For example, Rosa & Orey [15] stated that these translations are related to the interrelations between the local (emic) and academic knowledge (etic). These translations are addressed in order for the members of distinct cultural groups understand specific concepts acquired in the academia through the disciplines of ethnobiology, ethnoecology, ethnomedicine and, especially, ethnomathematics. For example, Barton [11] argues that ethnomathematics “is more like anthropology. Researchers such as Eglash et al. [17] and Rosa & Orey [15] use the term translation to describe the process of modelling local (emic) cultural systems, which may have Western (etic) mathematical representations. However, local designs may be merely analysed from a Western view such as the applications of symmetry classifications from crystallography to indigenous textile patterns. We understand that “using ethnomodelling as a tool towards pedagogical action of the ethnomathematics program, students have been shown to learn how to find and work with authentic situations and real-life problems”. In this regard, ethnomodelling can be considered as a promising research field in its initial evaluations of the influences on the academic achievements of the students as well it opens new possibilities for the development of anthropological research. On the other hand, ethnomathematical uses of modelling techniques establish relations between the local conceptual framework and the mathematical ideas embedded in relation to global designs through translations. In this regard, this relationship may be named as ethnomodelling because “the act of translation is more like mathematical modelling”. This context has allowed Eglash [17] to affirm that in some cases, “the translation to Western mathematics is direct and simple such as counting systems and calendars”, as well, there are cases in which mathematical ideas and concepts are “embedded in a process such as iteration in bead work, and in Eulerian paths in sand drawings” and are harder to explain or translate. Because mathematical knowledge arises from emic rather than etic origins, it is reasonable to expect that ethnomathematics can apply modelling procedures to establish relations between local conceptual frameworks and the mathematical ideas embedded in their designs [17]. In this regard, the emphasis of ethnomodelling takes in consideration the processes that help the construction and development of the scientific and mathematical knowledge, which includes collectivity, creativity, and inventivity. In so doing, it is impossible to imprison mathematical concepts in registers of univocal designation of reality because there are distinct systems that provide an unambiguous representation of reality as well as universal explanations [19]. According to this approach, mathematics is not conceived as a universal language because its principles, concepts, and foundations are not always the same everywhere around the world. The processes of production of scientific and mathematical ideas, procedures, and practices operate in the register of the interpretative singularities regarding the possibilities for symbolic construction of the knowledge in different cultural groups.

The emphasis of ethnomodelling tends to privilege the organization and presentation of mathematical ideas and procedures developed by the members of distinct cultural groups in order to facilitate its communication and transmission through generations. The elaboration of models that represent these systems are representations that help members of these groups to understand and comprehend the world by using ethnomodels, which link their cultural heritage with the development of their mathematical practices. It is our understanding that this approach may assist in the organization of pedagogical actions that occur in classrooms through the use of the emic and etic aspects of these mathematical practices.

Using an ethnomodelling perspective, emic constructs represent the accounts, descriptions, and analyses expressed in terms of conceptual schemes and categories that are regarded as meaningful and appropriate by the members of the cultural group under study, which is in accordance with perceptions and understandings deemed appropriate by the insider’s culture [20]. The validation of emic knowledge comes with a matter of consensus, which is the consensus of local people who must agree that these constructs match the shared perceptions that portray the characteristic of their culture. On the other hand, the etic constructs are accounts, descriptions, and analyses of mathematical ideas, concepts, procedures, and practices expressed in terms of the conceptual schemes and categories that are regarded as meaningful and appropriate by the community of scientific observers and researchers. An etic construct must be precise, logical, comprehensive, replicable, and observer-researcher independent. According to D’Ambrosio [2], researchers and investigators have to acknowledge and recognize that local people possess scientifically mathematical valid knowledge.

We argue that what is traditional, in the sense of mathematical modelling, does not fully consider the implications of unique and diverse cultural aspects of human social systems. The cultural component in this process is critical because its accounts “emphasize the unity of culture, viewing culture as a coherent whole, a bundle of [mathematical] practices and values” [21] that are incompatible with the rationality of the elaboration of traditional mathematical modelling process. However, in the context of mathematical knowledge, what is meant by the cultural component, varies widely and ranges from viewing mathematical practices as socially learned and transmitted to members of cultural groups to mathematical practices viewed as made up of abstract symbolic systems with an internal logic giving a symbolic system its mathematical structure. What we hope to do in ethnomodelling is to focus on the deeper aspects of mathematics developed in diverse contexts and away from what was formerly considered exotic. If the former is considered, then it is the process by which knowledge transmission takes place from one person to another that is central to elucidating the role of culture in the development of mathematical knowledge [2]. If the latter is considered, then culture plays a far-reaching and constructive role with respect to mathematical practices that cannot be induced simply through observation of these practices. The mathematical knowledge developed by the members of a cultural group often consists of abstract symbol systems whose form is the consequence of an internal logic. Researchers and students alike may learn the specific instances of the usage of that symbol system as well as derive from those instances a cognatically based understanding of the internal logic of the mathematical symbology system.

The Ethnomodel of landless peoples’ movement: measuring the land – brazil

Knijnik [22] proposed activities about the demarcation of land from research work with the participants of the Landless Peoples’ Movement (Movimento dos Sem Terra - MST) in Southern Brazil. The demarcation of land activity was about the method of cubação of the land, which is a traditional mathematical practice applied by the participants of this movement. The term cubação of the land is considered as the solution of problems of the measurement of land using diverse shapes.

For example, calculate the area of land with a quadrilateral shape that measures 114 meters x 152 meters x 90 meters x 124 meters (Figure 2).

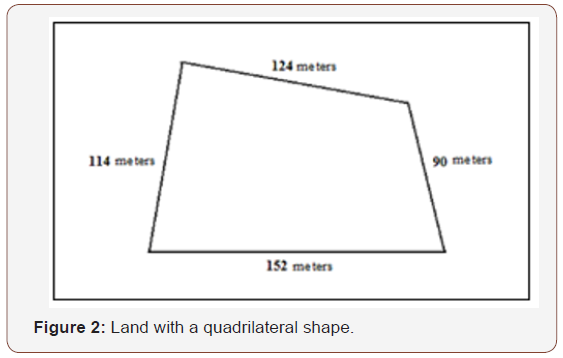
The mathematical knowledge of landless people can be represented by an ethnomodel that transforms the shape of the given land into a rectangle of 138 meters x 102 meter with an area of 14076 square meters (Figure 3).

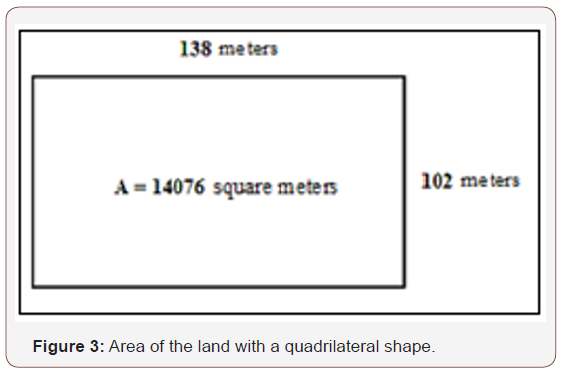
The model of this mathematical practice can be explained by the following ethnomodel:

a) Transform the shape of the irregular quadrilateral in a rectangle whose area can be easily determined through the application of the formula for area.

b) Determine the dimensions of the rectangle by calculating the mean of the two opposite sides of the irregular quadrilateral.

c) Determine the area of the rectangle by applying the formula A = b x h.

This particular type of mathematical knowledge pertaining to this cultural group consists of socially learned and transmitted mathematical practices, which represent the construction of ethnomodels of mathematical practices of social-cultural systems [1]. The cognitive aspect needed in this framework is primarily a decision process by which the members of cultural groups either accept or reject an ethnomodel as part of their own repertoire of mathematical knowledge. We understand that the conjunction of these two scenarios appears to be adequate to the depth needed to encompass the full range of cultural-mathematical phenomena because mathematical practices are socially learned and transmitted to the members of cultural groups. In this regard, they are made up of abstract symbolic systems with an internal logic, which gives its own mathematical structure.

In effect, there are two ways in which we recognize, represent and make sense of mathematical phenomena that we encounter:

1) There are often common forms of logic and cognition that we share, to varying degrees, with members of our own and other cultural groups. This is often attributed to a common worldview, paradigm, or cosmologies. As well, it may be attributed to the common human condition. This approach includes cognitive models that we may elaborate at a nonconscious level, which serves to provide an internal organization of external mathematical phenomena and to provide the basis upon which a mathematical practice takes place.

2) There is a culturally constructed representation of external mathematical phenomena that also provides an internal organization for this phenomena; but where the form of the representation arises through formulating an abstract, conceptual structures that provides both form and organization for external phenomena in a manner that needs not be consistent with forms and patterns of those phenomena as external phenomena; that is, the cultural construct provides a constructed reality.

The implications for mathematical modelling of systems taken from reality are that models of a cultural construct may be considered a symbol system organized by internal logic of members of cultural groups. A model built without a first-hand sense for the world being modelled should be viewed with suspicion [11]. In this regard, researchers and investigators, if not blinded by their prior theory and ideology, should come out with an informed sense of distinctions that make a difference from the point of view of the mathematical knowledge of people being modelled. Therefore, they should, in the end, be able to tell outsiders (global-etic) what matters to insiders (local-emic).

Modelling the tipi: an ethnomodelling example

Spatial geometry is inherent by the shape of the tipi and it was used to symbolize the universe in which many Plains People of North America lived. The word tipi from the Sioux language refers to a conical tent or dwelling common among the prairie peoples. According to Orey [20], the majority of Sioux tribes use the tripodal foundation (Figure 4) because it is stronger and offers a firmer foundation than a quadripodal foundation (Figure 4). In this context, the tripodal foundation of the Tipi appears to be perfectly adapted for the harsh environment in which it was used. It also has the advantage of providing a stable structure, was lightweight, and portable. It withstood the prevailing winds and extremely variable weather of this region in North America [12], For example, an ethnomodel explains why a tripod is more flexible than a quadripodal or four-legged structure. Imagine three points, A, B and C that are not collinear. There are an infinite number of planes that pass-through points A and B that contain the straight-line AB. Only one of these planes also passes through point C therefore we can say that three points are not collinear if they determine one plane. This means that these non-collinear points exist on one plane and that three collinear points do not determine the only plane. This can be explained using the postulate for the determination of a plane. In other words, given any three non-collinear points, there is only one plane to which exists these same three points. It is important to look at this information mathematically. The base formed by the tripod is ΔABC (Figure 5). The midpoints of each of the sides of ΔABC are points M, N and P (Figure 6).

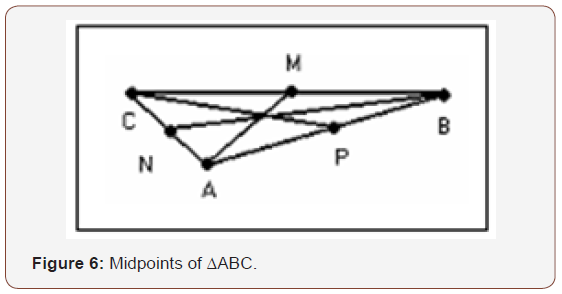
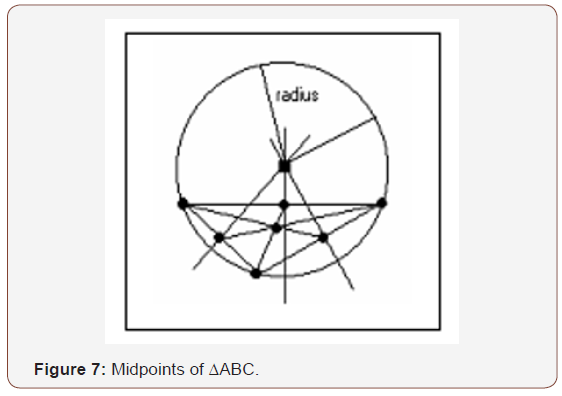
It is possible to match each vertex of ΔABC to the midpoint of each opposite sides that gives us the straight lines AM, BN, and CP. These straight lines form three medians, which are the straight lines connecting the midpoint of each opposite side of the triangle and its vertex. The medians intersect at only one point called centroid. Archimedes demonstrated that medians of a triangle meet at its balance point or centre of gravity. Native Americans placed their fire and altar at this point in the tipi. Cartographers call this point the geographic centre [14]. The dwellers determined the center of the circular base of the Tipi by using the idea of the existing triangle formed by the tripod. In this context, the center of the Tipi holds a definite power and holiness, which is more than just necessity or aesthetics that went into finding the center of the Sioux home (Figure 7). The tipi cover is folded in half and the poles are laid together before tying them to form the tri or quadripodal frame, which forms the foundational base for the Tipi structure.

The concepts of emic and etic were first introduced by the linguist Pike [24] who drew on an analogy with two linguistic terms. Phonemic, which is the sounds used in a particular language and phonetic, which is the general aspects of vocal sounds and sound production in languages. All possible sounds human beings can make constitute phonetics. However, when people actually speak a particular language, they do not use or hear all possible sounds. In this regard, as modelled by linguists, not all sounds make a difference because they are locally significant. This means that they are the phonemics of that language [24]. If we make an analogy with this approach to ethnomodelling, it is possible to state that the emic perspective is about differences that make mathematical practices unique from an insider’s point of view. We argue that emic models are grounded in what matters in the mathematical world of those being modelled. However, many models are etic in the sense that they are built on an outsider’s view of about the world being modelled. In this context, etic models represent how the modeller thinks the world works in the context of the person or group under study, through systems taken from their reality while emic models represent how people who live in such worlds think these systems work in their own reality.

The etic perspective always plays an important role in ethnomodelling research, yet the emic perspective should be also taken in consideration in this process because, in this perspective, the emic models sharpen the question of what an agent-based model should include to serve practical goals in modelling research. Thus, mathematical ideas and procedures are etic if they can be compared across cultures using common definitions and metrics while the focus of the emic analysis of these aspects are emic if the mathematical concepts and practices are unique to a subset of cultures that are rooted on the diverse ways in which etic activities are carried out in a specific cultural setting. While emic and etic are often thought to create a conflicting dichotomy, Pike [24] originally conceptualized them as complementary viewpoints. Berry [25] argued that rather than posing a dilemma, the use of both approaches can deepen our understanding of important issues in scientific research and investigations. Usually, in ethnomodelling research, an emic analysis focuses on a single culture and employs descriptive and qualitative methods to study a mathematical idea, concept, procedure, or practice of interest. An emic view focuses on the study within the cultural group context in which the researcher tries to develop research criteria relative to the internal characteristics or logic of the system of the cultural system. Thereafter, meaning is gained in relation to a specific environment and, therefore, not transferable to other contextual settings.

On the other hand, an etic analysis would be comparative, examining many different cultures by using standardized methods. The primary goal of the emic approach is a descriptive idiographic orientation of the mathematical phenomena because it puts emphasis on the uniqueness of each mathematical idea, concept, procedure, or practice. In contrast, the etic approach tries to identify lawful relationships and causal explanations valid across different contexts and cultures. Thus, if researchers and educators wish to make statements about universal or etic aspects of mathematical knowledge, these statements need to be phrased in abstract ways. Conversely, if they wish to highlight the meaning of these generalizations in specific or emic ways, then they need to refer to more precisely specified mathematical events. The etic perspective may be a way of getting at emics of members of distinct cultural groups, which is in accordance with the work of Pike [24]. In this regard, the etic perspective may be useful for penetrating, discovering, and elucidating emic systems developed by members of distinct cultural groups. We also would like to highlight that in the dialectical perspective, the etic perspective claims to knowledge of any given cultural group have no necessary priority over its competing emic claims. In this regard, the cultural specificity may be better understood with the background of communality and the universality of theories and methods and vice versa. The rationale behind the emic-etic dilemma is the argument that mathematical phenomena in their full complexity can only be understood within the context of the culture in which they occur. The emic approach tries to investigate the mathematical phenomena and their interrelationships and structures through the eyes of the people native to a particular cultural group.

Mathematical knowledge of members of cultural groups that is combined with the western mathematical/scientific paradigm and knowledge system may result in a dialectical perspective in mathematics education. An emic analysis of a mathematical phenomenon is based on internal structural or functional elements of a particular cultural group. An etic analysis is based on predetermined general concepts external to that cultural group [13]. The emic perspective provides internal conceptions and perceptions of mathematical ideas and concepts while the etic perspective provides the framework for determining the effects of those beliefs on the development of the mathematical knowledge. In this regard, the acquisition of mathematical knowledge is based on the applications of current mathematics curriculum, which is assessed based on multiple instructional methodologies across various cultures. Academic failure is complex, but one reason for this universal problem may be related to curriculum developers who have ignored the emic perspectives in the mathematics curriculum that they construct for school use. An emic-etic perspective includes the recognition of other epistemologies, and of holistic and integrated natures of the mathematical knowledge of members of diverse cultural groups found in many urban centres. In this regard, an ethnomodelling practice provides an ideological basis for learning with and from the diverse cultural and linguistic backgrounds of members of distinct cultural groups [1]. However, an etic construct is a mathematical-theoretical idea that is assumed to apply in all cultural groups while an emic construct is the one that applies only to the members of specific cultural groups. This means that a cultural bias occurs if researchers assume that an emic construct is actually etic that results in an imposed etic perspective in which a culture-specific idea is wrongly imposed on the members of other cultures.

The elements of an ethnomodelling curriculum can be helpful in the process of designing emic-etic pedagogical approaches that are integrative, participative, relevant, and use self or community as an object of learning. These elements and the nature of the previous mathematical knowledge of the students lend themselves easily to the principle of sequencing in curriculum development. By giving educators the freedom to start with the previous mathematical knowledge and experience of their students, we can move from the familiar to the unfamiliar and from the concrete to the abstract in the process of promoting the acquisition of mathematical knowledge through modelling process. In this context, an emic-etic perspective in an ethnomodelling curriculum practice provides the underlying philosophy of knowledge generation and exchange within and between all subsystems of mathematics education [20-25].

Today, numerous diverse mathematical knowledge systems are at risk of becoming extinct because of rapidly changing natural and cultural environments and fast pacing economic, social, environmental, political, and cultural changes occurring on a global scale. In this context, many local mathematical practices often disappear because of the intrusion (colonization) by foreign technologies or resulting of the development concepts that promise short-term gains or solutions to problems faced by cultural groups without being capable of sustaining them. The usefulness of emic and etic distinctions is evident. Like all human beings, researchers, educators, and teachers have been enculturated to some particular cultural worldview, and they therefore need a means of distinguishing between the answers they derive as enculturated individuals and the answers they derive as observers. Defining emics and etics in epistemological terms provides a reliable means of making that distinction. Culture is a lens, shaping reality, and a blueprint, specifying a plan of action. At the same time, a culture is unique to a specific group of people. By utilizing the research provided by both approaches, we gain a more complete understanding of the cultural groups of interest. An alternative goal for ethnomodelling research must be the acquisition of both emic and etic knowledge. Emic knowledge is essential for an intuitive and empathic understanding of mathematical ideas of a culture and it is essential for conducting effective ethnographic fieldwork. Etic knowledge is essential for cross-cultural comparison, the essential components of ethnology, because such comparisons that necessarily demand the use of standard units and categories. Furthermore, emic knowledge is a valuable source of inspiration for etic hypotheses.

Finally, we define ethnomodelling as the study of mathematical phenomena within a culture because it is a social construction and culturally bound. This perspective forms the basis for significant contributions of an ethnomathematical perspective in re-conceiving the discipline of mathematics and in a pedagogical action in the mathematics classrooms. Using the tripod tipi as a metaphor, ethnomodelling creates a firm foundation that allows us to integrate emic, etic, and dialogic approaches in exploring mathematical knowledge. This metaphor can support the construction and development of ideas as to how mathematics in diverse contexts originated and was used and can help us to understand and share how members of diverse cultural groups can decolonize educational frameworks. And, most importantly, this allows us to unpack ways in which science and mathematics have been used across time and place.

None.

No Conflict of Interest.

1. Rosa M (2010) A mixed-methods study to understand the perceptions of high school leader about English language learners (ELL): The case of mathematics. Unpublished doctorate dissertation, College of Education, California State University, Sacramento, California.
2. D’Ambrosio U (1990) Etnomatemática (Ethnomathematics). São Paulo, Editora Ática, Brazil.
3. Rosa M and Orey DC (2016), Humanizing mathematics through ethnomodelling. Journal of Humanistic Mathematics, Vol 6(2), pp 3-22.
4. Rosa M and Orey DC (2006) Abordagens atuais do programa etnomatemática: delinenando-se um caminho para a ação pedagógica [Current approaches in ethnomathematics as a program: Delineating a path toward pedagogical action]. Bolema, Vol 19(26), pp 19-48.
5. Smith LT (1999) Decolonizing methodologies: research and indigenous peoples. Otago Press, pp. 39, London, England.
6. Battiste M, Bell Lynne, Findlay L (2002) Decolonizing education in Canadian universities: an interdisciplinary indigenous research project. Canadian Journal of Native Education 26(2): 82-95.
7. Joseph GG (1991) The crest of the peacock. IB Tauris & Co, London.
8. Needham J (1959) Science and civilization in China. Cambridge University Press, pp. 79 Cambridge, England.
9. Eglash R (1997) When math worlds collide: intention and invention in ethnomathematics. Science, Technology and Human Values 22(1): 79- 97.
10. Kay P (1971) Explorations in mathematical anthropology. MIT Press, Cambridge.
11. Barton B (1996) Making sense of ethnomathematics: Ethnomathematics is making sense, Educational Studies in Mathematics. 31(1): 201-233.
12. Ascher M (2002) Mathematics elsewhere: an exploration of ideas across cultures. NJ: Princeton University Press, USA.
13. Closs MP (1986) Native American mathematics. University of Texas Press, Texas, USA.
14. Orey DC (2000) The ethnomathematics of the Sioux tipi and cone: Mathematics Across Culture: The History of Non-Western Mathematics. In Selin H (Ed.) Kulwer Academic Publishers, Dordrecht, Netherlands, pp. 239–252.
15. Rosa M, Orey D (2009) Symmetrical freedom quilts: the ethnomathematics of ways of communication, liberation, and art. Revista Latinoamericana de Etnomatemática 2(2): 52-75.
16. Urton G (1997) The social life of numbers. A Quechua ontology of numbers and philosophy of arithmetic. University of Texas Press, Texas, USA.
17. Eglash R, Bennett A, O’Donnell C, Jennings S, Cintorino M (2006) Culturally situated designed tools: Ethnocomputing from field site to classroom. American Anthropologist 108(2): 347-362.
18. Rosa M, Orey DC (2010) Ethnomodelling: A Pedagogical Action for Uncovering Ethnomathematical Practices. Journal of Mathematical Modelling and Application 1(3): 58-67.
19. Craig E (1998) Routledge encyclopedia of philosophy: Questions to sociobiology. Vol 8, Routledge, New York, USA.
20. Lett J (1996) Emic-etic distinctions. Encyclopedia of Cultural Anthropology In: Levinson D and Ember M (Eds.), Henry Holt and Company, New York, pp. 382-383.
21. Pollak R, Watkins S (1993) Cultural and economic approaches to fertility: Proper marriage or mésalliance? Population and Development Review 19: 467-496.
22. Knijnik G (1996) Exclusão e resistência: educação matemática e legitimidade cultural (Exclusion and resistance: mathematics education and cultural legitimacy). Brazil.
23. Pike KL (1954) Emic and etic standpoints for the description of behaviours. IL: Summer Institute of Linguistics, Vol 31, Glendale, California.
24. Berry JW (1999) Emics and etics: A symbiotic conception. Culture & Psychology 5(2): 165-171.
25. François K, Pinxten R, Mesquita M (2013) How anthropology can contribute to mathematics education. Revista Latinoamericana de Etnomatemática 6(1): 20-39.