Theoretical Approach to Predict the Size of Skyrmion

Dzyaloshinskii-Moriya interaction (DMI) in magnetic systems plays a key role to generate skyrmions which is localized topological objects [1-6]. There are two types of magnetic skyrmions, so called Bloch and Néel skyrmions as shown in Figure 1. While the Bloch skyrmions are related with the bulk DMI, the Néel skyrmions in systems related with interfacial DMI [7,8].

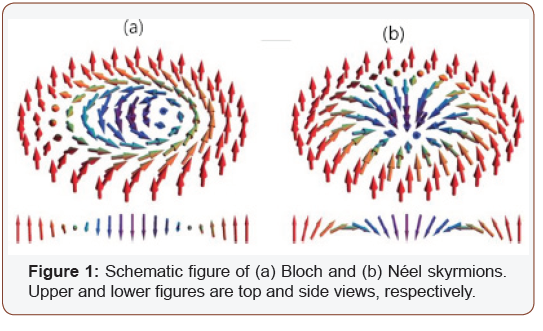
In the field of spintronics and information processing devices, magnetic skyrmions have been considered as promising candidates due to their unique properties. Because of the DMI, relatively small size skyrmions with diameter of only few nanometers have been discovered in recent studies. Also, they have a better stability compared to traditional magnetic bubbles. In perspective of the driven current density, extremely low value with order of 10⁶ Am² is observed compared to that for magnetic domain walls with order of 10¹² Am².

These days a lot of knowledge about the DMI-induced magnetic skyrmions has been gathered. However, each contribution of the exchange energy (A), magnetic anisotropy energy (K) and strength of DMI (D) which are the important material parameters on skyrmion radius (R) is still not clear.

In this paper, we confirmed that the skyrmion profiles agree well with the 360° domain wall formula. With this formula as an ansatz, we obtain the anlytical expressions of the skyrmion size R and the skymion wall width d as function of A, D, K, and B by minimizing the energy with respect to R and d as two independent quantities. Moreover, these theoretically obtained results agree well with experiments.

A two-dimensional (2D) ferromagnetic film is considered in xy plane with total energy of E = E_ex + E _DM + E _an + E _Ze, where E_ex, E_DM, E_an. And E_Ze represent the exchange energy, the DMI energy, the anisotropy energy, and the Zeeman energy, respectively. Each term can be written as

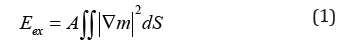
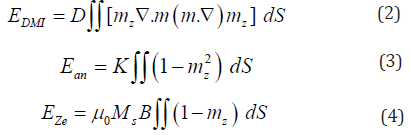
The integration is over the whole film. While Ms is a constant saturation magnetization, m is the unit vector of M_s. For the reference energy defined as E=0, we choose the energy of single domain state of mz=1. The demagnetization energy is included in Ean by using the effective anisotropy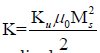obtained by the shape anisotropy, where K_u is the perpendicular magnetocrystalline anisotropy. Since it is convenient to use a polar coordinate due to the rotating behavior of skyrmion, a skyrmion centered at r=0 is described by,Ѳ=Ѳ(r), Φ =υ φ +γ , with boundary condition of Ѳ(0)=0(π) and Ѳ(∞)= π(0). Here, υ and γ are the vorticity and a constant classifying type of skyrmions. υ=1 is for a skyrmion and υ=-1 is for an anti skyrmion. While γ=0 or π is for Néel skyrmions,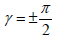 is for Bloch skyrmions

By using the radius of the m_z=0 contour, we define the skymion size R. It also can be defined by skyrmion polarity

If p=1, spins in the inner and outer domains pointing to the -z and +z-directions, respectively. In the opposite way, p=-1 represents the +z and -z-directions in the inner and outer domains, respectively.

In terms of Ѳ, four energy terms for υ=1 are

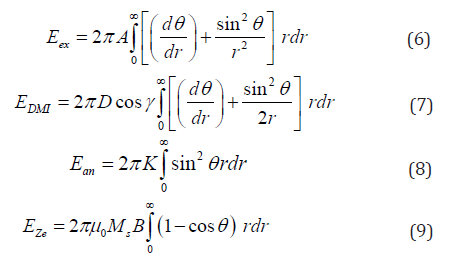
For a skyrmion of p=1, because Ѳ gradually decreases from Ѳ(0)= 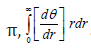should be smaller than 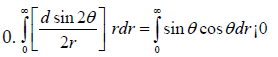for from the skyrmion wall. Also, sign of sinθ cosθ changes from negative to positive during passing through from the inner to outer domain. Thus, γ=0(π) for D¿0(¡0)is necessary to get lower total energy. Sine the magnetization profile looks like a 360° Néel domain wall along a radial direction, we consider the Walker-like 360° domain wall solution which described as,

Then the skyrmion energy can be collected from Eq (10) by using the Walker-like 360° domain wall profile Ѳ_dw(r). In general, the total energy depends on R and d described as

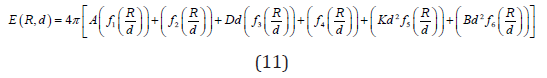
where fi(x) non-elementary function which is defined below. For the exchange energy, by defining x=R/d, t=r/d, we have

Therefore, we define

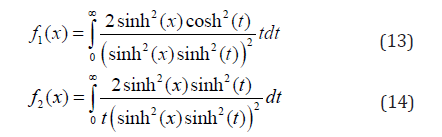
For DMI energy, we have

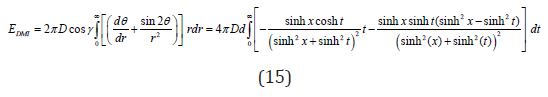
Therefore,

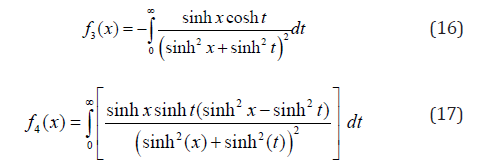
For the anisotropy energy, we have

For the wall region and the skyrmion core, the Zeeman energy is non-zero. Therefore, the function f₆ is

E (R, d) is minimized by skyrmion size R and wall width d.

Figure 2 and Figure 3 are numerical results and they are clearly show that skyrmion can be discovered for D<3.75mJ/m² in the present case. There are minimized values of the E (R, d) if |D|<3.75mJ/m² that indicates existence of skyrmion. However, above the upper limit, the stable state is stripe domains instead of a skyrmion. In cases with much weak strength of D, a single domain that state with all spins pointing up or down might become the most stable state. That also exhibit a minimal A of around 15pJ/m and a minimal K of around 0.56MJ/m³, below where skyrmion does not exist, and the stable state is stripe domains. The skyrmion size increases with D. however decreases with K, A and B, which is consistent with the experimental observations.

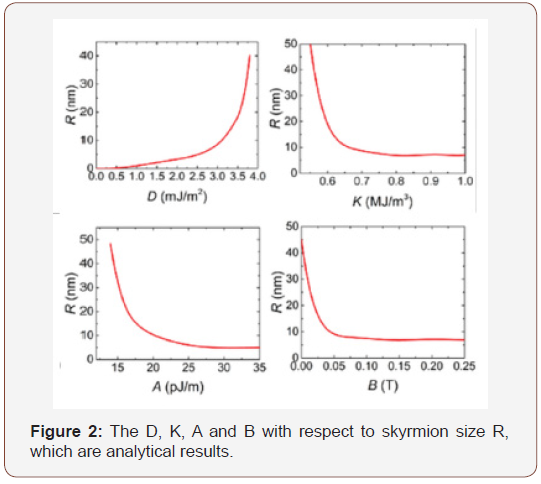
The exchange and DMI energies are caused by the spatial magnetization variation rate. For a single skyrmion, the magnetization variation rate in the radial direction scales as 1/d while and tangent direction scales as 1/R. Then the exchange energy is proportional to skyrmion wall area of Rd multiplying the square of the magnetization variation rates 1/R²+1/d²,

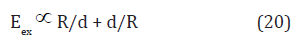
For a Néel skyrmion, the magnetization variation rate along the tangent direction is perpendicular to m and does not contribute to the DMI energy. The DMI energy is then proportional to wall area (Rd) multiplying the magnetization variation rate along radial direction (1/d),

EDMI ∝ R (21)

The anisotropy energy is mainly from the skyrmion wall area,

Ean ∝ Rd (22)

The inner domain and wall are determining the Zeeman energy in the skyrmions. The inner domain and the wall area are proportional to its area of π(Rcd)2 and πRd, respectively. In case of R >>d, sinh(x)cosh(x) ≈ e^x. Thus, function g(t,x) can be written as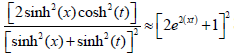 Since g(t,x) is definitely non-zero only near t = x, we could understand to observed phenomenon that E_ex, E_DMI , and E_an are predominantly from skyrmion wall region which is expected to be very narrow.

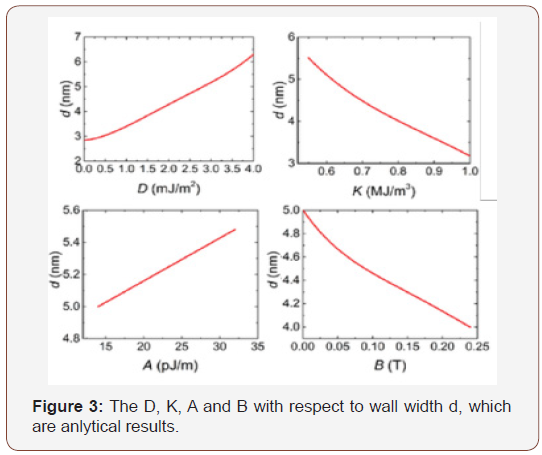
We found that a 360° domain wall profile parametrized by size and wall width of skyrmion, and an obtained domain wall profile can well describe a single skyrmion. When the analytical expressions of the size and wall width of skyrmion with respect of the DMI strength, magnetic anisotropy, exchange stiffens and external field are obtained, these formulas agree well with experiments.

None.

No conflict of interest.

1. S Mühlbauer, B Binz, F Jonietz, C Pfleiderer, A Rosch, et al. (2009) Skyrmion Lattice in a Chiral Magnet. Science 323(5916): 915-919.
2. X Yu, Onose Y, Kanazawa N, Park JH, Han JH, et al. (2010) Real-space observation of a two-dimensional skyrmion crystal. Nature 465(7300): 901-904.
3. Rössler UK, Bogdanov AN, Pfleiderer C (2006) Spontaneous skyrmion ground states in magnetic metals. Nature 442(7104): 797-801.
4. S Heinze, Kirsten von Bergmann, Matthias Menzel, Jens Brede, Andre Kubetzka, et al. (2011) Spontaneous Atomic-Scale Magnetic Skyrmion Lattice in Two Dimensions. Nature Physics 7(9): 713-718.
5. A Jackson, Jackson AD, Pasquier V (1985) The skyrmion-skyrmion interaction. Nuclear Physics A 432(3): 567-609.
6. Iwasaki J, Mochizuki M, Nagaosa N (2013) Current-induced skyrmion dynamics in constricted geometries. Nat Nanotechnol 8(10): 742-747.
7. M Belmeguenai, Jean-Paul Adam, Yves Roussigné, Sylvain Eimer, Thibaut Devolder, et al. (2015) Interfacial Dzyaloshinskii-Moriya interaction in perpendicularly magnetized Pt/Co/AlO_x ultrathin films measured by Brillouin light spectroscopy. Phys Rev B 91(18): 180405.
8. Hans T Nembach, Justin M Shaw, Mathias Weiler, Emilie Jué, Thomas J Silva (2015) Linear relation between Heisenberg exchange and interfacial Dzyaloshinskii–Moriya interaction in metal films. Nature Physics 11: 825-829.