The Correct Indentation Stiffness and Modulus Can Be Obtained from the Loading Curve

The stiffness or rigidity S is force difference over deformation difference. SuchΔFN/ Δh expression is nothing else than a mathematical differentiation. That was previously not realized and makes the unloading curves with all their well-known unsolved problems unnecessary. We just can forget about all of the assumptions, iterations, and adjustments with them. And by also using the loading curve’s physical lawF_N = k h3/2 from them with the unit of k (e.g. mN/μm3/2) [1], we obtain by simple mathematic differentiation the stiffness for the indentation modulus asS= kΔh^3/2 Δh and thus S = k 1.5 h0.5. The k is a constant, as long as no phase-transition occurs. We have thus different stiffness values S and moduliE_phys = 1.5 S/ A0.5 (we call it E_phys as it is correct by physically deduction for pyramidal and conical indentations. By differentiation of the loading curve. For the standard Berkovich one has the basic area Abasic = a 31/2/4 but it takes the side area A_side3^0.5tan^2β h² _pyr/sinβ for different polymorphs and pyramidal indenters. Clearly, log-log plots are no reliable means for visually claiming their linearity [2]. The assumption of “linearity up to F_max” and thus “elastic indentation modulus” (it is after an inelastic loading) ends at every kink in close correspondence with the correctly analyzed loading curve. Conversely an “h2”, as used for the loading curve by [2] and DIN-ISONIST would provide no straight line but a useless curved “FN vs h2 plot”. From falsely assumed FN vs h2 loading curves we do not obtain constants in FN vs h2 curves. It is therefore not understandable how Shorshorov’s relation (as cited by [2]) for the “dP/dh =(2/π _{1/ 2} ) Er A1/2” has been deduced and always used for “Berkovich indentations, accordingly”. But theπ in such formula would somehow suggest that it was thought for a cone but not for a pyramid. Such Shorshorov’s relation-deduction paper is not found in the internet, but hundreds of users just cite it falsely in their papers, even though they could not have read a paper of Shorshorov or from his Russian coworkers. Even if these mean pseudo-cones for simulating“equivalent” pyramids they behave nevertheless unequal [3]. Thus, instead of “2π ^1/2 = 1.12838” this factor for S must by the correct factor to read 1.5 from the differentiation result.

The peak load for the modulus calculation is misleading it might be any load within the linearity of the F_N vs h^3/2 loading curve [1]. However at any kink position due to phase transition the slope changes until the next kink etc. and finally to the maximal load, because every polymorph has its characteristic mechanical properties. We must now recall in Table 1 how complicated the modulus story is with respect to meaning, techniques and in particular anisotropies.

Table 1: Elastic Moduli of α-Quartz (trigonal with 6 independent Young’s moduli from Crystran’s Handbook at 106; 87; 58; -18, 13; 7 GPa, where C means stiffness = compliance C11=87 C12=7 C44=58 C13=13 C14= (−)18 C33=106 are the ultimate data from RUS (relaxation ultrasound spectroscopy).

The Alternative Technique in [12] gives no experimental data, but only changes the area function iteration and uses the “stiffness measurement technique”of [2] with changed parameters, but the imaged hardness and modulus values above 0.5 μm displacement are drawn close to the earlier values and there seem to be enormous initial very small values starting with zero values.

We at first have to check whether elastic modulus is correct, because the indentation process is not reversible due to the inverse pyramidal hole that persists after the retraction of the indenter. Clearly upon indentation we use vertical and sidewise forces and thus energy. But while the sidewise energy-producing pressure had been put to zero by [2] with violation of the energy law, as complained in [8], such pressure has been freely used for the elasticity by [2]. This energy is from the remaining pressure part that is used for the shifting of the material within the crystal and also to phase-transition, to mostly less voluminous polymorph after a phase-transition onset. Such pressure release undoubtedly re-widens the material’s impression volume for its earlier interface with the indenter upon the retraction of the tip with release of pressure less in deep region and more near to the surface. That is the reason for the unloading curve, but why is only a short linear part close to the surface considered? The released energy adds up all along the unloading curve along the side faces of the pyramidal indenter: We really see an elastic effect, as multiple on/off traces forth and back are possible. But that happens only at the side faces of the pyramid, not at its basic area, where [2] and all their followers’ world-wide claim it with the projected area of the unloading pyramid. It is not related to any of the other techniques in Table1. It is particular important that such processes are with respect to the pyramid’s side surface but not with respect to the projected pyramidal base. That is the gravest and unpardonable error in the DIN-ISO-NIST production of stiffness and modulus by the calculation from unloading curves of indentations. It leads to final depth dependences, because the side faces of the pyramid increase enormously with higherdepth, whereas the fictional pyramidal basic face stays constant. We mention here the enormous deviation of the fictionalα -quartz modulus in comparison with the other values of Table 1 (no depth and crystal face are given). Our own cube corner hardness values of 2006 on 5 different crystal phases show interesting anisotropies also for unloading moduli also for SrTiO3 [9]. But apart from anisotropy occurrence also with unloading moduli these experiments require repetition with the present loading-curve moduli.

The inelastic production of an inverted pyramidal hole can be microscopically imaged. Importantly, according to the physical deduction of the indentation the non-penetrating energy part is 20% [10] and it is elastically released by lifting off the indenter from the inverted pyramidal surface when it reinstalls it by lifting off the indenter from the inverted pyramidal surface when it reinstalls it under pressure. It is an unpardoned error of unloading moduli that they fictionally relate to the base of the pyramid rather than its side areas. That error is not made for the side areas moduli that only relate to the mantle faces of the pyramid, where the moduli only rely upon.

We show it with tungsten and how that differs with the unloading stiffness of [2] (410 GPa. The hardness values of the polymorphs are also compared to show the error of integration over its kink.

We deduce now the comparison of multiply unphysical unloading moduli of [2] and the correct physical moduli E_phys from the loading curves:

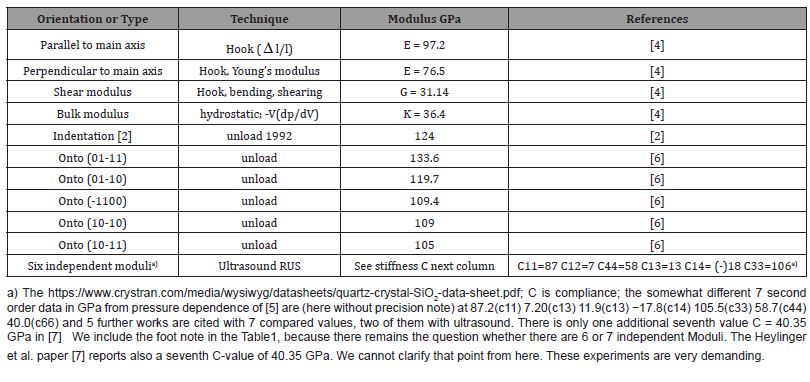
The sidewise force of 0.2 F_N works upon the lateral surfaces of the Berkovich indenter. And this 20% value of the loading fraction covers all effects, which include phase-transition, sinking-in, or pile-up that are not used for the penetration next to the pressure. But it is part of the stiffness and modulus. The total lateral surface of the Berkovich indenter mantle has been published [6,11] as 26.96756h_Berkovich².This value is the dividend under the force, and we obtain (any axis-cut Fa should be subtracted) Δ F_N / Δ side-force from zero toThis value is the dividend under the force, and we obtain (any axis-cut Fa should be subtracted) Δ F_N / Δ side-force from zero to F_kink or F_max for the stiffness Sphys. These physical values can be converted to E_phys = 1.5 S/A0.5. Everybody is advised to use these Formulas (1) to (3) and the correct transformation into the modulus E_phys for receiving the formulas (1), (2) and (3) and E_phys.

Table 2: Hardness, Stiffness, and Moduli of Tungsten with Berkovich Indenter.

The author’s work does not use the unphysical hardness and moduli, but he provides physical hardness (slope of the linear FN vs h3/2 plot) before and after the kink unsteadiness: here k1= 95.57 and k2 = 114.50 mN/μm3/2, resp. The normalized phase-transition energy is calculated from these to give 8.563 mNμm/μm or 0.07051 mNμm/mN ([6], Chapter 8).

The calculation of the exact Stiffness and Modulus values can be easily calculated by also using the formulas of the cited Reference [6]. But I do not choose here a totally unreasonable dangerous DINISO- NIST “Stiffness” and “Modulus” value of tungsten for comparing with such type of increadible errors in this short communication.

we do not need unloading curves for obtaining unphysical mechanical property values such as unloading stiffness and indentation modulus. The loading curve is inelastic, but the pressure along the indenter side faces after its impression release are elastically released, because the on/off repetitions are repeatable. They are elastic from an inverted pyramidal hole area with increasing concentration from zero to maximal at the surface.

All indentation moduli that continue to be calculated from the unloading curves must be replaced by those from the differentiation of the loading curves. That is also valid for the previous already called “physical moduli”, which were however only improvements of the then known common unloading moduli with the false relation to the pyramidal basis area. Also these must be replaced by the new physical moduli that do not. These formulas distinguish also the there found polymorphs with their onsets at and above the sufficiently high characteristic forces. That is urgently important as the stiffness or moduli are used for the numerous further mechanical that are listed in Table 3.

Problems with incorrect elastic moduli of DIN-ISO-NIST are disastrous because of their use in various widespread applications. These are listed in Table 3 and require all widespread corrections with the new E_phys

Table 3: Some Applications of Elastic Modulus E, as used for Mechanical Properties of all Solid Materials, Including Viscoelastics with Modulus E instead of E_phys via Differentiation of the Loading Curve.

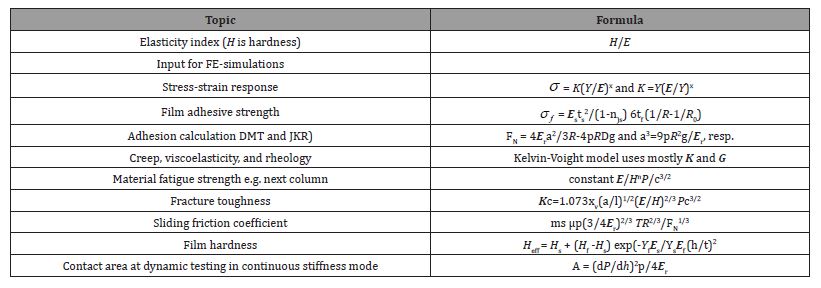
This Table 3 was redrawn from figure 5.3. in [6], here for showing that the indentation elasticity E (in fat) is used for at least 11 very different mechanical characterizations. These are amply used in the worldwide appearing publications. The application of these must not be discussed here, but all of these quite complicated material’s properties are falsified by the use of the unphysical unloading modulus. That is dangerously disastrous and must be healed by the differentiated loading curve’s modulus E_phys, as developed in this paper.

This short Communication is an important timely warning from multiply false unloading stiffness for being used to numerous mechanical applications (Table 3). It is for preventing damage of technical materials and constructions (e.g. bridges, earth quakes, etc.). Mathematical derivations and integrations are forbidden over kink unsteadiness in the linearized F_N vs h^3/2 loading curve. That is also true for stiffness and hardness that leave only a very minimal number of indentation curves without phase-transitions [6,10]. Their non-identification with the false h2 (instead of h3/2) [1] is a very severe error, and a rather shameful error is the relating of stiffness to the basic area rather than to the side areas of a pyramid. We can the therefore very complicated comparison not treat in a short communication, but I repeat the formula for the three Berkovich side areas: 3 Aside = 3 3^0.5 tan² β hpyr 2/sinβ the value for Berkovich is26.96756h² _Berkovich [11]. After all, the multiply false unloading moduli do not deserve a comparison with the now described correct ones for every different polymorph.

The author thanks Dr. Rainer Koch, from the University of Oldenburg for his help in running the author’s computer through all problems with improvements, novelties, and necessary repairs after all attack to it including breakdowns.

The author declares that there is no conflict of interest.

1. Kaupp G (2016) The Physical Foundation of F_N = k h^3/2 for Conical/Pyramidal Indentation Loading Curves. Scanning 38(2): 177-179.
2. Oliver W C, Pharr G M (1992) An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing¸ Open Access Indentation Experiments. J. Mater. Res 7: 1564-1583.
3. Kaupp G (2022) The Non-Equivalence of Pyramids and their Pseudo-Cones: Important New Insights. J. Applied Mathematics and Physics 10: 1158-1166.
4. Crystran Handbook (2023); https//issuu.com/crystran/docsHandbook
5. Calderon et al. (2007), Complete Determination of the Elastic Moduli of α-Quartz under Hydrostatic Pressure up to 1GPa: an Ultrasonic Study. J Phys Condens Matter 19(43): 436228.
6. Kaupp G (2022) Basic Mathematics for Physically Correct Mechanical Properties from Indentations. E-Book covering 16 open-access publications; ISBN 978-93-5547-9211.
7. Heylinger P, Ledbetter H, Kim S A (2002) Elastic Constants of Natural Quartz. J. Acoustic Society of America 114(2): 644-50.
8. Kaupp G (2025) Worldwide Shameful Violation of the Energy Law from 1992 till now by Academy and Industry. Modern Concepts in Material Science 7(3): 2025.
9. Kaupp G (2006) Atomic Force Microscopy, Scanning Near field Optical Microscopy and Nanoscratching. Application to Rough and Natural Surfaces, Heidelberg New York.
10. Kaupp G (2013) Penetration Resistance: A New Approach to the Energetics of Indentations. Scanning 35(6): 392-401.
11. Kaupp G (2021) Volume, Side-Area, and Force-Direction of Berkovich and Cubecorner Indenters, Novel Important Insights. Adv. Materials Physics and Chemistry 11(11): 212-241.
12. Oliver W C (2001) Alternative Technique for Analyzing Instrumented Indentation Data. Journal of Materials Research 16(11): 3202-3206.