Positron Impact Excitation of the nS, nP, and nD States of Atomic Hydrogen

The well-known relativistic wave equation was formulated in 1928 by Dirac [1]. He combined the ideas of relativity and quantum mechanics to formulate the equation and predicted an antiparticle of spin ħ/2. He assumed that the antiparticle must be a proton because at that time only two particles namely proton and electron were known. However, Hermann Weyl, from symmetry consideration, suggested that the positive particle must have the same mass as that of an electron. Later on, this particle came to be known as a positron. The positron was discovered in cosmic rays by Anderson [2] in a cloud chamber in 1932. Positrons and electrons can form positronium atoms which annihilates giving a 511 MeV line with a width of 1.6 keV. This line has been seen from the center of galaxy. Positrons have been detected on the sun, stars, and in the interstellar medium [3]. They have been used in medicine (PET scan) to study the human brain. They have been used to probe Fermi surfaces to find defects in metal surfaces. Over the years, there have been many laboratory studies. Allan Mills [4] produced negative positronium ion and then studied its photo detachment. Similarly, there have been many calculations on positron systems.

We calculated scattering of positrons from hydrogen atoms, annihilation, and positronium formation [5,6] and reference therein. Burke et al. [7] and Morgan [8] carried out close-coupling calculations to calculate excitation cross section of the 2S state of the hydrogen atom. In this method, the total wave function is expanded in terms of the eigenstates of the target. This method gives the polarizability of the target provided a large number of P states is included. The polarizability of the hydrogen atom is 4.5 (a0)3. Including only 2P state gives only 66% of the polarizability. Walters [9] has used a close-coupled pseudo state approximation to calculate 1S to 2S and 2P excitation cross sections. Kernoghan et al. [10] have used a 33-state close-coupling approximation which includes eigenstates of hydrogen and positronium atoms. We carried out such calculations of the nS states, n being 2 to 6, using the distorted wave approximation [11,12]. Equations (1- 14) in reference [11] give the formulation of these calculations. In the above mentioned calculations [5,6,11,12], we used the hybrid theory [13] to calculate scattering functions. In this approach, the long-range and short-range correlations are taken into account at the same time and the theory is variationally correct. The calculated phase shifts have lower bounds, which implies that they are below the correct results. Results obtained using the hybrid theory agreed well with the results of the previous calculations.

Replacing the bound state 2S function in Eq. (13) of [11] by a bound state function for which the excitation is desired, we carry out calculations for excitation of nP and nD as indicated in [11]. We used 30 partial waves to achieve converged results for excitation cross sections. We need more partial waves as the incident ene is increased. In Table 1, we give excitation cross sections for P and D states. In Table 2, we give results for elastic and excitation cross sections. Excitation cross sections for the S states are taken from [11,12]. The maximum of excitation cross sections is at k=1.40.

Table 1:Excitation Cross sections (π (a0)2) of nP and nD states, n=2 to 6 of atomic hydrogen using the variational polarized orbital method with l_max=29.

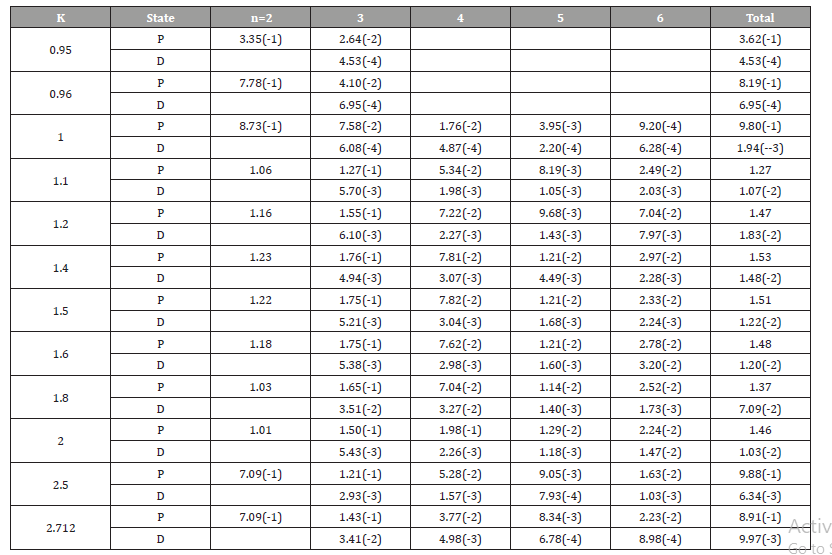
Table 2:Contribution from various states to the total cross section (π (a₀)²).

Total cross sections for the positron-hydrogen scattering have been measured by Zhou et al. [14]. These measurements include all the possible processes. The present results are lower than the experimental results as it should be. There are no direct measurements of the excitation cross sections.

Excitation sections for 1S to nS, nP, and nD by positron impact have been calculated at various positron impact energies by using the hybrid theory of scattering which includes the long-range and the short-range correlations. This approach is variationally correct. The calculated phase shifts have lower bounds to the exact phase shifts. The maximum of the elastic and excitation cross sections is at k=1.4. The present results might encourage measurements of excitation cross sections.

None.

No conflict of interest.

1. PA Dirac (1971) Development of Quantum Theory, Gordon and Breach Science Publications. pp. 59.
2. CD Anderson (1933) The positive Electron. Phys Rev 43(6): 491-494.
3. RJ Murphy, GH Share, JG Skibo, B Kozlovsky (2005) The Physics of Positron Annihilation in the Solar Atmosphere. Astrophys J Suppl Ser 161: 495-591.
4. AP Mills Jr (1981) Obsevation of Positronium Negative Ion. Phys Rev Lett 46: 717-720.
5. AK Bhatia (2016) Positron-Hydrogen Scattering, Annihilation and Positronium Formation. Atoms 4(4): 27.
6. AK Bhatia (2017) P-wave Positron-Hydrogen Scattering, Annihilation and Positronium Formation. Atoms 5(2): 17.
7. PG Burke, HM Schey, K Smith (1963) Collision of Slow Electrons and Positrons with Atomic Hydrogen. Phys Rev 129: 1258.
8. LA Morgan (1982) Positron impact excitation of the n=2 level of hydrogen. J Phys B 15: L25-L29.
9. HRJ Walters (1988) Positron scattering by atomic hydrogen at intermediate energies: 1s to 1s, 1s to 2s, and 1s to 2p transitions. J Phys B 21: 1893-1906.
10. AA Kernoghan, DJR Robinson, HRJ Walters (1996) Positron scattering by atomic hydrogen. J Phys B 29: 2089-2102.
11. AK Bhatia (2019) Positron Impact Excitation of the 2S State of Atomic Hydrogen. Atoms 7(3): 69.
12. AK Bhatia (2019) Positron Impact Excitation of the nS State of Atomic Hydrogen. Atoms 8(1): 9.
13. AK Bhatia (2007) Hybrid theory of electron-hydrogen scattering. Phys Rev A 75(3): 032713.
14. S Zhou, WE Kappila, CK Kwan, TS Stein (1994) Measurement of total cross sections for positrons and electrons colliding with atomic hydrogen. Hyperfine Interactions 89: 483-487.