Mechanomagnetic Spectroscopy: A Review

The Piezoelectric Ultrasonic Composite Oscillator Technique (PUCOT) [1-3] is used to study the internal friction in materials. In such technique, quartz transducers are used to induce resonant oscillations at ultrasonic frequencies in bar-shaped samples. In our laboratory, the basic experimental PUCOT system was improved with several additions. We designed a cryostat to change the temperature during the experiments. Besides, a coil to apply polarizing fields was introduced in order to measure magnetic effects in the internal friction, as the magneto mechanical damping. Lately it was thought that, due to the reversible Villari Effect (RVE), the use of PUCOT under polarizing applied fields should produce measurable stress-induced induction in materials. To measure it, the experimental set-up of PUCOT was modified by the addition of a pick-up coil around the samples. Such experiments were successful, and the new developed technique was called Mechanomagnetic Spectroscopy (MMS) [4]. First measurements of stress-induced induction showed only positive values and some unexpected zero values. It was thought that we recorded the magnitude (modulus, absolute value) of the signal and some of such zeros could correspond to the transition between positive and negative values. To check this hypothesis a lock-in amplifier was introduced to measure the phase of the signal with reference to the oscillatory applied stress. Successfully, 180° shifts in the phase were measured. Such result implicated a change of the sign at zero points, as it was expected [5]. The last step in the development of the MMS was to relate the measured stress-induced induction to the reversible inverse and direct magnetostriction [6]. Nowadays we can consider the MMS as a fully developed technique.

As it was stated, we apply an oscillatory stress (in the order of 90 kHz) to bar-shaped samples (typical size of 1x1x15 mm3) by means of quartz transducers. The length of the sample depends on the Young Modulus in the following way:

Equation (1)

E=4ρl²f²,

where ρ is the density, l the length, and f the fundamental resonant frequency of the sample, respectively. The oscillatory strain in the sample produces a stress-induced induction in magnetic samples Citation: ML Corró. Mechanomagnetic Spectroscopy: A Review. Mod Concept Material Sci. 3(3): 2020. MCMS. MS.ID.000561. DOI: 10.33552/MCMS.2020.03.000561 Page 2 of 4 due to the RVE. To measure it, it was conceived to place a pickup coil around the maximum strain section of the sample since a voltage would be generated due to the Faraday’s law. Such voltage can be estimated in the following way:

Equation (2)

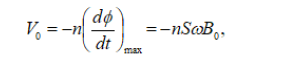
with n the number of turns in the coil, S the cross section of the sample, w the angular frequency and B0 the amplitude of the stress-induced induction in the sample. Such voltage is amplified and the real and imaginary parts (in phase and out of phase with the applied stress) are obtained by means of a lock-in amplifier. As MMS is based in the PUCOT, we can measure not only the B0 but also the elastic and anelastic properties simultaneously. With such data we can attempt to calculate de direct magnetostriction [6].

Direct and inverse magnetostrictions are connected by a Maxwell type relation [7]:

Equation (3)

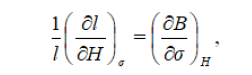
where l is the length of the sample, H is the magnetic field, B is the induction and σ is the stress.

Taking into account that direct magnetostriction is λ = Δl/l, we can consider the application of a polarizing field H* and integrate (3) to obtain

Equation (4)

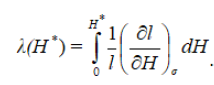
If there is no hysteresis, the differential inverse magnetostriction is approximately equal to reversible inverse magnetostriction [6]:

Equation (5)

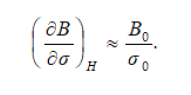
Besides, equation (2) can be approximated as [6]: Equation (6)

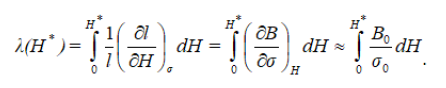
Typical working condition of our equipment are temperature range T≈ 80-400 K, frequency ≈90-100 kHz, strain amplitude (which is related to the stress by the Young Modulus) 𝜀0≈10-7 10-4, and polarizing field H=0-18 kA/m. Measurements can be achieved as a function of temperature, H and 𝜀0.

Figure 1 depicts the full experimental MMS equipment [8].

We can see a more detailed picture of the cryostat rod in Figure 2 [9].

The arrangement of the sample is shown in Figure 3 [9].

The great advantage of MMS is the great sensitivity. Data can be recorded at a magnetic field as low as Earth’s one for demagnetized samples [4]. Moreover, MMS is proposed to be a more sensitive method to detect magnetic hysteresis than the registration of conventional B(H) loops [10].

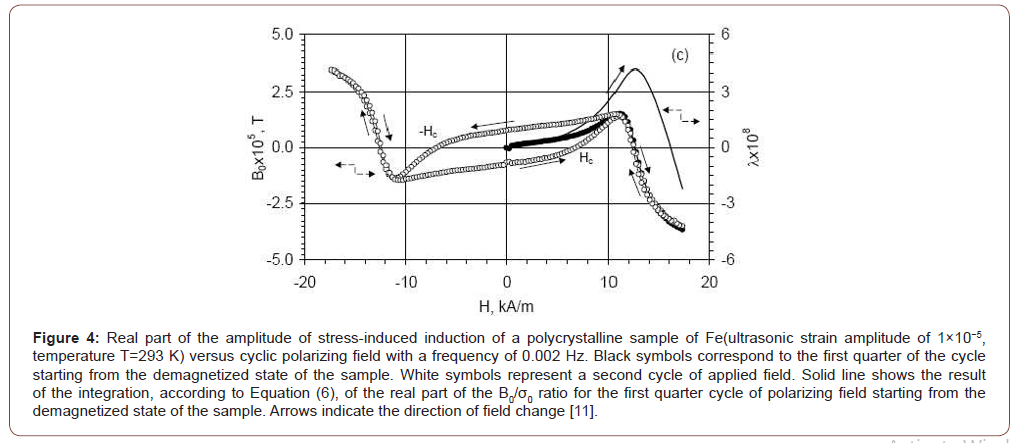
Figure 4 shows the data of a typical measurement as a function of polarizing field H [11]. The sample is polycrystalline Fe. Round symbols represents the stress-induced induction and the solid line the result of the integration, according to Equation (6), of the real part of the B0/σ0 ratio for the first quarter cycle of polarizing field starting from the demagnetized state of the sample. Arrows indicate the direction of field change. The calculated direct magnetostriction has the correct behavior. Nevertheless, the values are substantially lower than the real ones [12-13]. It can be explained by the fact that reversible inverse magnetostriction measured in the ultrasonic frequency range is substantially lower than the static one [14].

However, it gives valuable information of the sign of magnetostriction hard to obtain with other techniques at so low fields Figure 4.

Use of MMS allowed the observation in ferromagnetic shape memory alloy (FSMA) Ni-Fe-Ga-Co of a temperature - magnetic field domain wherein magnetoelastic coupling demonstrates variations of sign and analysis of magnetic domain wall dynamics in polycrystalline ferromagnetic martensite [5]. It was also found in Ni-Fe-Ga-Co that the reversible inverse magnetostriction, and therefore the magnetoelastic coupling, changes its sign close to the Curie temperature [6]. Such phenomenon depends on the crystallographic orientation [15]. In Dy it was found a Villari critical point (a temperature where magnetoelastic coupling is zero without dependence of polarizing applied field) near 166 K. Below such temperature a time-dependent relaxation of RVE was discovered [16]. Such point is also related to essential features of magnetic hysteresis and AC susceptibility on heating from the ferromagnetic state [10]. MMS permitted to introduce generalized coercitivity of magnetoelastic hysteresis and it demonstrated the same exponents of scaling power laws in the ferro- and antiferromagnetic phase. It could be attributed to the similarity of hindering mechanisms impeding the mobility of domain walls in antiferromagnetic and ferromagnetic phases [17].

MMS equipment will be improved with a new cryostat to take measurements near 10 K. Currently different crystallographic orientations of Dy single crystals are studied [18]. Future experiments will be focused in several rare earth elements as Gd and Ho, as well as new ferromagnetic shape memory alloys, without discarding other magnetic materials.

MMS is a very versatile and fully developed technique. We can achieve data of magnetostriction, elastic and anelastic properties simultaneously under very different conditions of temperature and polarizing field. It’s outstanding sensitivity allow us to obtain new exceptional results.

The author would like to acknowledge S Kustov for his help and support for the last years.

The author declares no conflict of interests of any type.

1. WH Robinson, A Edgar (1974) The Piezoelectric Method of Determining Mechanical Damping at Frequencies of 30 to 200 KHz. IEEE Trans Son Ultrason 21(2): 98-105.
2. G Gremaud, S Kustov, Ø Brenes (2001) 9.2 Ultrasonic techniques: PUCOT and Act, ed. Schaller, G. Fantozzi, and G. Gremaud, “Mechanical Spectroscopy Q-1 2001, with Applications to Materials Science”, “Mechanical Spectroscopy Q-1 2001, with Applications to Materials Science”, Materials Science Forum, Switzerland, pp. 652-666.
3. S Kustov, S Golyandin, A Ichino, G Gremaud (2006) A new design of automated piezoelectric composite oscillator technique. Mater Sci Eng A 442(1-2): 532-537.
4. S Kustov, F Masdeu, E Cesari (2006) Mechanomagnetic spectroscopy of phase transitions in ferromagnetic shape memory alloys. Appl Phys Lett 89: 061917.
5. S Kustov, ML Corró, E Cesari (2009) Mechanomagnetic spectroscopy of ferromagnetic shape memory alloys, Mater Sci Eng A 521–522: 194-200.
6. S Kustov, ML Corró, E Cesari, JI Pérez-Landazábal, V Recarte (2010) Peculiarities of magnetoelastic coupling in Ni–Fe–Ga–Co ferromagnetic martensite. J Phys D: Appl Phys 43(17): 175002.
7. RM Bozorth (2003) Ferromagnetism. ed. J Willey, IEEE Press, Piscataway, NJ, USA.
8. ML Corró (2010) Magnetoelastic coupling and internal friction in Ni-Fe-Ga type alloys. PhD thesis, 190 pp, 76.
9. ML Corró (2010) Magnetoelastic coupling and internal friction in Ni-Fe-Ga type alloys, PhD thesis, 190 pp, 77.
10. Iu Liubimova, MLC Moyà, J Torrens-Serra, V Recarte, JI Perez-Landazabal, et al. (2017) Low Field Magnetic and Thermal Hysteresis in Antiferromagnetic Dysprosium. Metals 7(6): 215.
11. ML Corró (2010) Magnetoelastic coupling and internal friction in Ni-Fe-Ga type alloys, PhD thesis, 190 pp, 90.
12. RM Bozorth (2003) Ferromagnetism. ed. J Willey, IEEE Press, Piscataway, NJ, USA.
13. E Du Trémolet de Lacheisserie, D Gignoux, M Schlenker (2005) Magnetism: Fundamentals, Springer, New York.
14. LS Pravdin (1982) Soviet. J Non-Destructive Testing 18: 613.
15. ML Corró, YI Chumlyakov, J Torrens-Serra, S Kustov (2013) Peculiarities of magnetoelastic coupling in Ni₅Fe_21.5Ga₂₇ single crystals. J Phys D: Appl Phys 46(37): 375002.
16. ML Corró, A El Hichou, E Cesari, S Kustov (2016) Study of magnetic transitions in Dy by means of reversible Villari effect. J Phys D: Appl Phys 49(1): 015001.
17. Iu Liubimova, ML Corró, J Torrens-Serra, V Recarte, JI Perez-Landazabal, et al. (2017) Scaling of low field magnetoelastic hysteresis in antiferromagnetic Dy. Materials Physics and Mechanics 32(1): 43-50.
18. S Kustov et al. unpublished work.